22.5 等腰梯形(2) 课件(14张PPT)
文档属性
| 名称 | 22.5 等腰梯形(2) 课件(14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 162.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览


文档简介
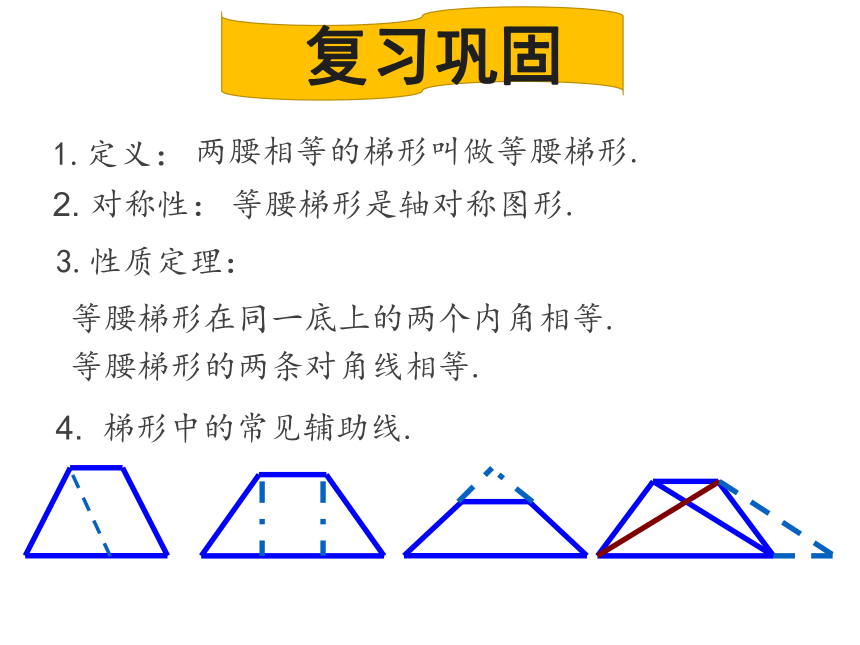
课件14张PPT。1.定义:复习巩固2. 对称性:3.性质定理:4. 梯形中的常见辅助线.等腰梯形是轴对称图形.
两腰相等的梯形叫做等腰梯形.等腰梯形在同一底上的两个内角相等.
等腰梯形的两条对角线相等.两腰相等的梯形是等腰梯形。1、定义判定:∵AD∥BC,AD≠BC∴ 四边形ABCD是梯形又∵AB=CD∴ 四边形ABCD是等腰梯形梯形的证明 四边形ABCD中,AD∥BC,但AD≠BC, AB=CD的条件下,左图是等腰梯形吗?∵AD∥BC,AB=CD,
∴梯形ABCD是等腰梯形.几何语言:想一想:等腰梯形还有没有其他的判定方法呢?
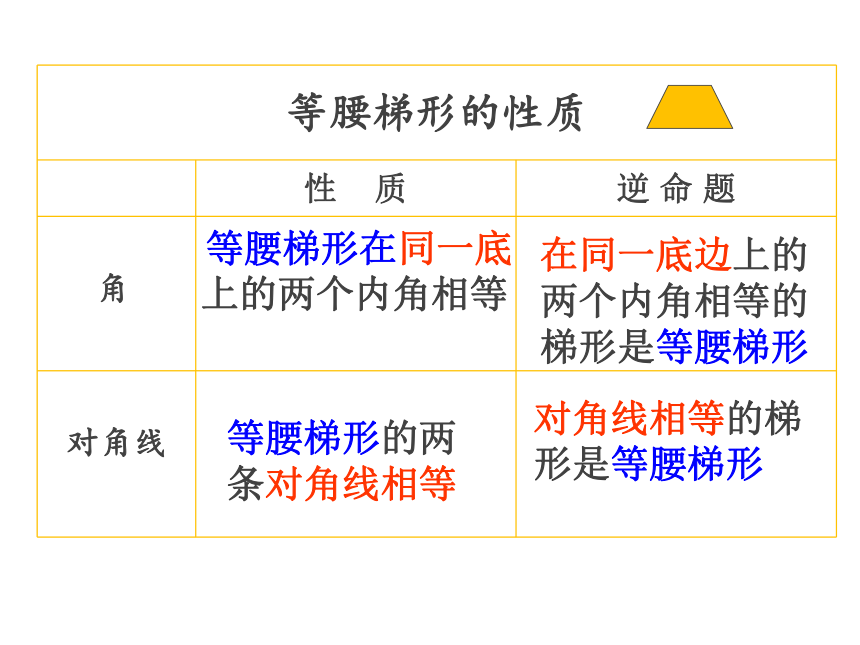
等腰梯形性质定理的逆命题能作为新的判定依据吗?等腰梯形的判定 等腰梯形在同一底上的两个内角相等等腰梯形的两条对角线相等在同一底边上的两个内角相等的梯形是等腰梯形对角线相等的梯形是等腰梯形如图,已知:在梯形ABCD中,AD∥BC,∠B=∠C .
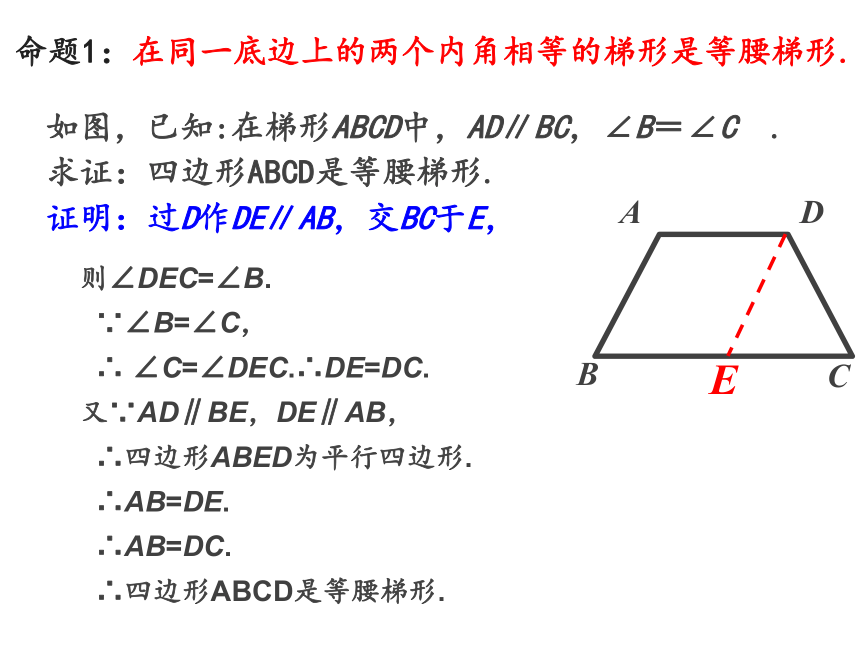
求证:四边形ABCD是等腰梯形.证明:过D作DE∥AB,交BC于E,则∠DEC=∠B.
∵∠B=∠C,
∴ ∠C=∠DEC.∴DE=DC.
又∵AD∥BE,DE∥AB,
∴四边形ABED为平行四边形.
∴AB=DE.
∴AB=DC.
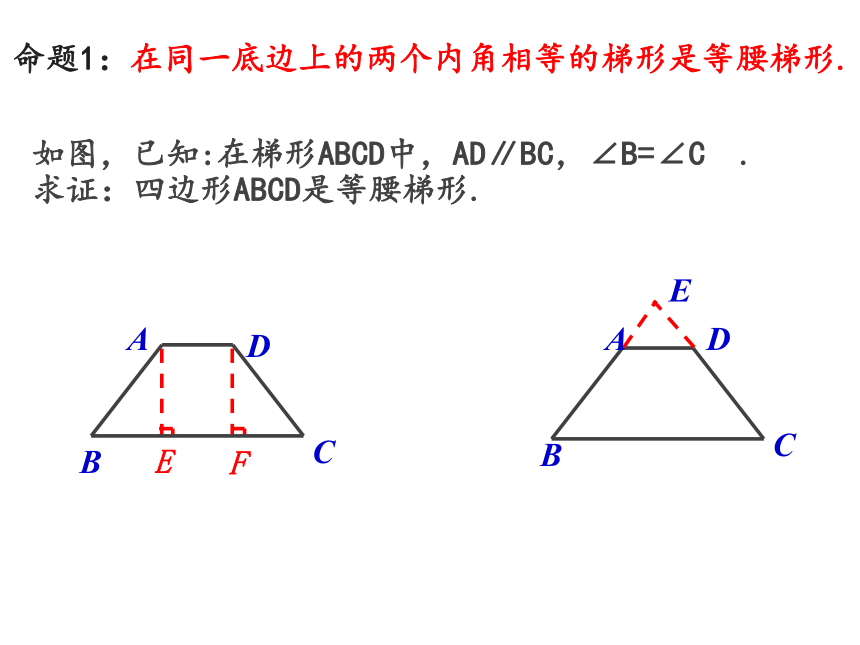
∴四边形ABCD是等腰梯形.命题1:在同一底边上的两个内角相等的梯形是等腰梯形.如图,已知:在梯形ABCD中,AD∥BC,∠B=∠C . 求证:四边形ABCD是等腰梯形.E命题1:在同一底边上的两个内角相等的梯形是等腰梯形. 几何语言:
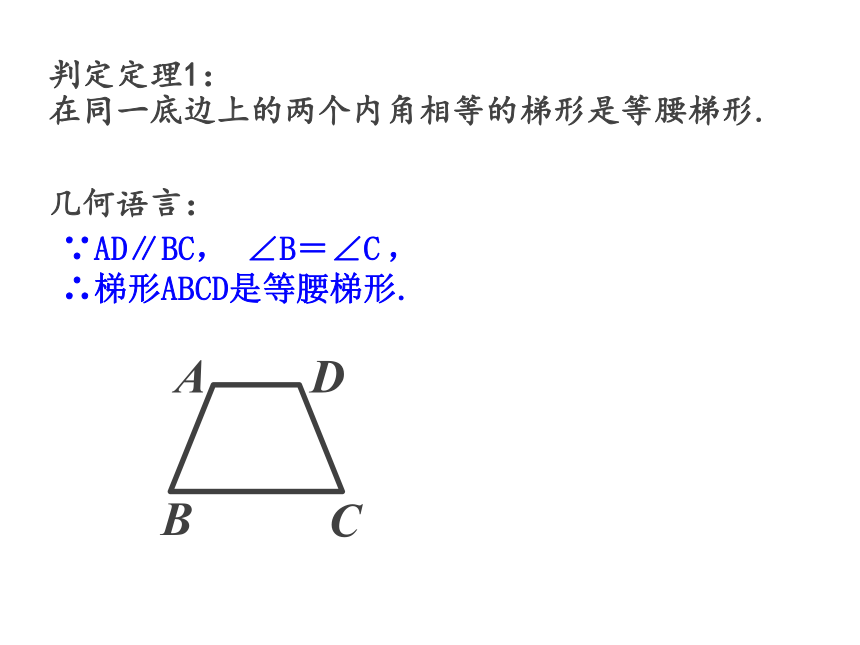
判定定理1: 在同一底边上的两个内角相等的梯形是等腰梯形.∵AD∥BC, ∠B=∠C ,
∴梯形ABCD是等腰梯形. 命题2:对角线相等的梯形是等腰梯形.已知:在梯形ABCD中,AD∥BC,AC=BD.
求证:四边形ABCD是等腰梯形.E又 AD∥BC,
∴ 四边形ACED为平行四边形. ∴ DE=AC .∵ AC=BD ,
∴ DE=BD.
∴ ∠1=∠E . 又∵ ∠2=∠E , ∴ ∠1=∠2 .
又 AC=DB,BC=CB,
∴ ΔABC≌ΔDCB.
∴ AB=CD.
∴四边形ABCD是等腰梯形.证明:过点D作DE∥AC,交BC的延
长线于点 E12 几何语言:
判定定理2: 对角线相等的梯形是等腰梯形.∵AD∥BC, AC=BD,
∴梯形ABCD是等腰梯形.例题 1
如图,梯形ABCD中,BC∥AD, DE∥AB,DE=DC,∠A=100 °,求梯形其他三个内角的度数.解: ∵ BC∥AD, DE∥AB,
∴四边形ABED是平行四边形,
∴AB=DE.
又DE=DC,
∴AB=DC,
∴梯形ABCD是等腰梯形.
∴ ∠C =∠B=180 °-∠A=80 °,
∠ADC= ∠A=100 °.交流小结基础训练1.抢答题 判断正误:
(1) 有两个角相等的梯形一定是等腰梯形. ( )(5) 两条对角线相等的梯形一定是等腰梯形. ( )(3) 对角互补的梯形一定是等腰梯形. ( )(4) 一组对边平行,另一组对边相等的四边形一
定是等腰梯形. ( )(2) 有两个内角是70o的梯形一定是等腰梯 形 . ( )一起做一做2. 下列说法中,错误的是( )
A.有一组对边平行,另一组对边相等的梯形
是等腰梯形
B.有一组对角互补的梯形是等腰梯形
C.有一组邻角相等的四边形是等腰梯形
D.同一底上的两个内角相等的梯形是等腰梯形作业:
1、课后作业 22.5(2)
2、练习册 22.5(2)
两腰相等的梯形叫做等腰梯形.等腰梯形在同一底上的两个内角相等.
等腰梯形的两条对角线相等.两腰相等的梯形是等腰梯形。1、定义判定:∵AD∥BC,AD≠BC∴ 四边形ABCD是梯形又∵AB=CD∴ 四边形ABCD是等腰梯形梯形的证明 四边形ABCD中,AD∥BC,但AD≠BC, AB=CD的条件下,左图是等腰梯形吗?∵AD∥BC,AB=CD,
∴梯形ABCD是等腰梯形.几何语言:想一想:等腰梯形还有没有其他的判定方法呢?
等腰梯形性质定理的逆命题能作为新的判定依据吗?等腰梯形的判定 等腰梯形在同一底上的两个内角相等等腰梯形的两条对角线相等在同一底边上的两个内角相等的梯形是等腰梯形对角线相等的梯形是等腰梯形如图,已知:在梯形ABCD中,AD∥BC,∠B=∠C .
求证:四边形ABCD是等腰梯形.证明:过D作DE∥AB,交BC于E,则∠DEC=∠B.
∵∠B=∠C,
∴ ∠C=∠DEC.∴DE=DC.
又∵AD∥BE,DE∥AB,
∴四边形ABED为平行四边形.
∴AB=DE.
∴AB=DC.
∴四边形ABCD是等腰梯形.命题1:在同一底边上的两个内角相等的梯形是等腰梯形.如图,已知:在梯形ABCD中,AD∥BC,∠B=∠C . 求证:四边形ABCD是等腰梯形.E命题1:在同一底边上的两个内角相等的梯形是等腰梯形. 几何语言:
判定定理1: 在同一底边上的两个内角相等的梯形是等腰梯形.∵AD∥BC, ∠B=∠C ,
∴梯形ABCD是等腰梯形. 命题2:对角线相等的梯形是等腰梯形.已知:在梯形ABCD中,AD∥BC,AC=BD.
求证:四边形ABCD是等腰梯形.E又 AD∥BC,
∴ 四边形ACED为平行四边形. ∴ DE=AC .∵ AC=BD ,
∴ DE=BD.
∴ ∠1=∠E . 又∵ ∠2=∠E , ∴ ∠1=∠2 .
又 AC=DB,BC=CB,
∴ ΔABC≌ΔDCB.
∴ AB=CD.
∴四边形ABCD是等腰梯形.证明:过点D作DE∥AC,交BC的延
长线于点 E12 几何语言:
判定定理2: 对角线相等的梯形是等腰梯形.∵AD∥BC, AC=BD,
∴梯形ABCD是等腰梯形.例题 1
如图,梯形ABCD中,BC∥AD, DE∥AB,DE=DC,∠A=100 °,求梯形其他三个内角的度数.解: ∵ BC∥AD, DE∥AB,
∴四边形ABED是平行四边形,
∴AB=DE.
又DE=DC,
∴AB=DC,
∴梯形ABCD是等腰梯形.
∴ ∠C =∠B=180 °-∠A=80 °,
∠ADC= ∠A=100 °.交流小结基础训练1.抢答题 判断正误:
(1) 有两个角相等的梯形一定是等腰梯形. ( )(5) 两条对角线相等的梯形一定是等腰梯形. ( )(3) 对角互补的梯形一定是等腰梯形. ( )(4) 一组对边平行,另一组对边相等的四边形一
定是等腰梯形. ( )(2) 有两个内角是70o的梯形一定是等腰梯 形 . ( )一起做一做2. 下列说法中,错误的是( )
A.有一组对边平行,另一组对边相等的梯形
是等腰梯形
B.有一组对角互补的梯形是等腰梯形
C.有一组邻角相等的四边形是等腰梯形
D.同一底上的两个内角相等的梯形是等腰梯形作业:
1、课后作业 22.5(2)
2、练习册 22.5(2)
