22.5(1) 等腰梯形的性质 课件(12张PPT)
文档属性
| 名称 | 22.5(1) 等腰梯形的性质 课件(12张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 176.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览


文档简介
课件12张PPT。22.5(1)
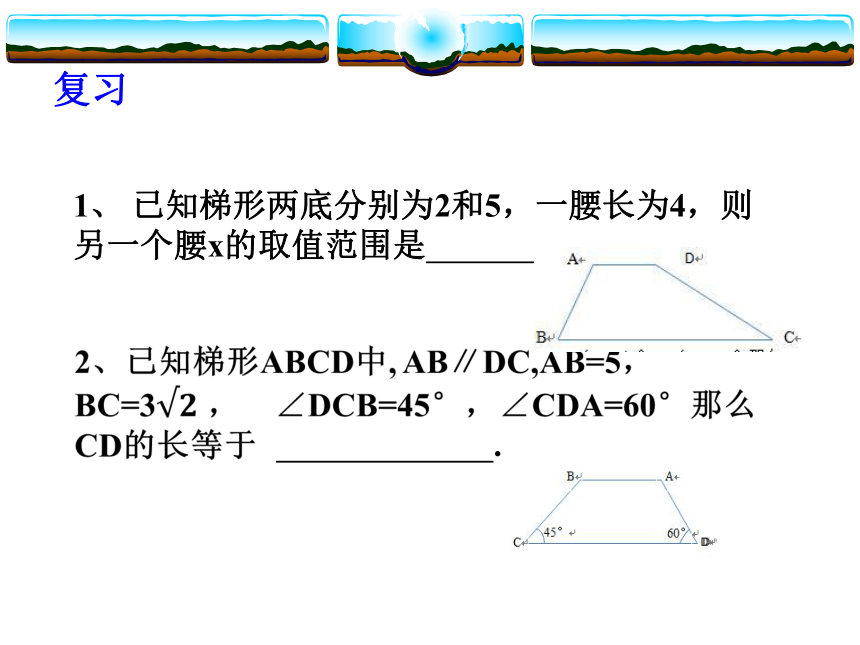
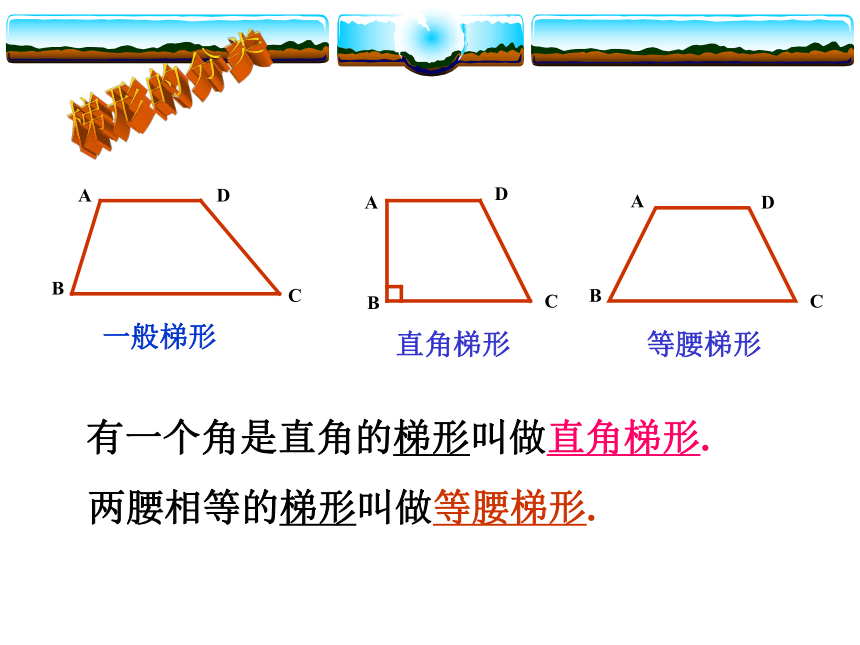
等腰梯形的性质复习1、 已知梯形两底分别为2和5,一腰长为4,则另一个腰x的取值范围是 .一般梯形直角梯形等腰梯形有一个角是直角的梯形叫做直角梯形.两腰相等的梯形叫做等腰梯形.梯形的分类 ABCD ABCCD
A
BD你能猜想等腰梯形有什么性质吗?等腰梯形的性质:(1)边:
(2)角:
(3)对角线:
(4)对称性:轴对称图形.两底边平行,
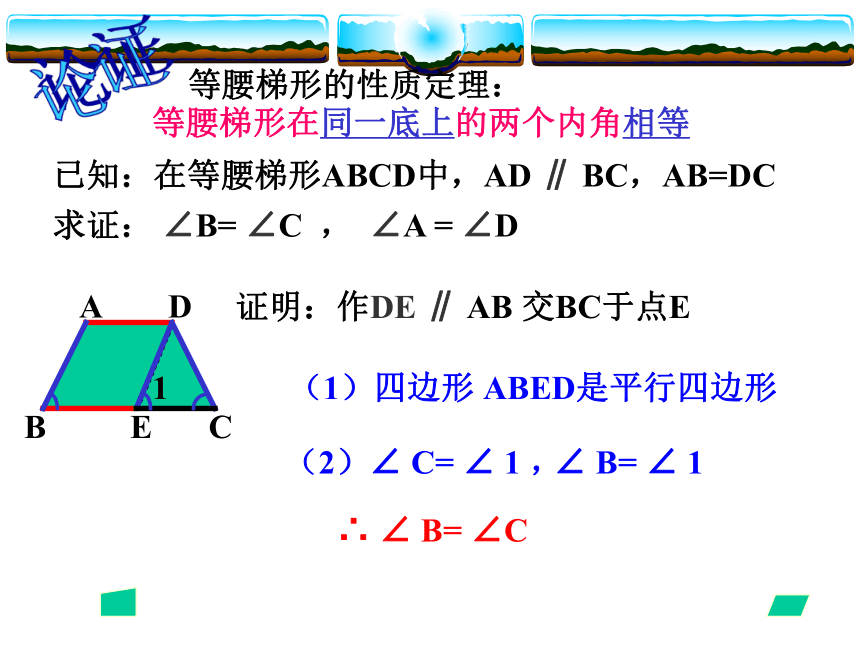
两腰相等.等腰梯形在同一底上的两个内角相等.等腰梯形的两条对角线相等.对称轴——两底中点所在直线论证等腰梯形在同一底上的两个内角相等等腰梯形的性质定理:ABCDE1已知:在等腰梯形ABCD中,AD ∥ BC,AB=DC求证: ∠B= ∠C , ∠A = ∠D证明:作DE ∥ AB 交BC于点E
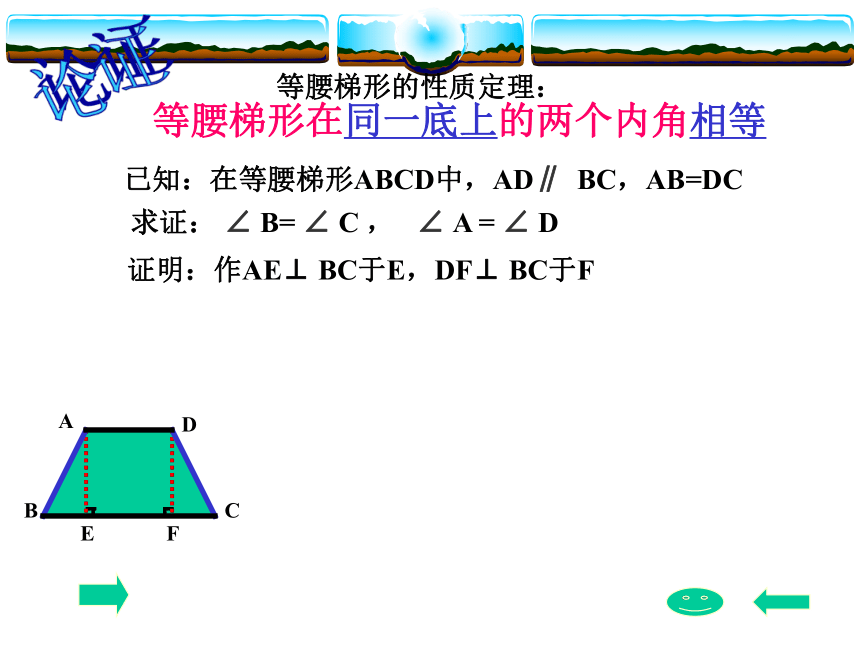
(2)∠ C= ∠ 1 ,∴ ∠ B= ∠C (1)四边形 ABED是平行四边形∠ B= ∠ 1 论证等腰梯形在同一底上的两个内角相等等腰梯形的性质定理:ABCD已知:在等腰梯形ABCD中,AD∥ BC,AB=DC求证: ∠ B= ∠ C , ∠ A = ∠ DEF证明:作AE⊥ BC于E,DF⊥ BC于F ABCDE 四边形ABCD是等腰梯形,延长两腰BA,
CD后交于点E,问△EBC和△EAD的形状如何?探索与研究∵四边形ABCD是等腰梯形, AD∥BC
∴ ∠ B= ∠ C ∴EB = EC∴ △EBC是等腰三角形∵ AD∥BC∴ ∠B= ∠EAD,∠C = ∠EDA∴EA = ED∴ △EAD是等腰三角形∴∠EAD = ∠EDA又∵ ∠ B= ∠ C (等腰梯形同一底上的两个内角相等)证明: △EBC和△EAD都是等腰三角形论证求证:等腰梯形的对角线相等ABCD已知:在等腰梯形ABCD中,AD ∥ BC,AB=DC12求证: AC=BD证明: ∵ ABCD是等腰梯形,AD∥BC
∴ ∠ ABC= ∠ DCB 又∵ AB=DC BC=CB∴ △ ABC≌△DCB ∴AC=BDO(OB = OC OA = OD)(等腰梯形同一条底边上的两个内角相等)1、如图:等腰梯形ABCD中,AD//BC,BA=CD,
E是AD延长线上一点,CE=CD
求证:∠B=∠E 考虑:四边形ABCE是平行四边形吗?为什么?2、如图:等腰梯形ABCD中,AD//BC,
AD=AB, BD⊥CD,
求:∠C的度数。等腰梯形中常用的添线方法作 高平移腰平移腰平移对角线延长两腰六、布置作业:
1、温习课本P93---94页;
2、学案22.5(1)
等腰梯形的性质复习1、 已知梯形两底分别为2和5,一腰长为4,则另一个腰x的取值范围是 .一般梯形直角梯形等腰梯形有一个角是直角的梯形叫做直角梯形.两腰相等的梯形叫做等腰梯形.梯形的分类 ABCD ABCCD
A
BD你能猜想等腰梯形有什么性质吗?等腰梯形的性质:(1)边:
(2)角:
(3)对角线:
(4)对称性:轴对称图形.两底边平行,
两腰相等.等腰梯形在同一底上的两个内角相等.等腰梯形的两条对角线相等.对称轴——两底中点所在直线论证等腰梯形在同一底上的两个内角相等等腰梯形的性质定理:ABCDE1已知:在等腰梯形ABCD中,AD ∥ BC,AB=DC求证: ∠B= ∠C , ∠A = ∠D证明:作DE ∥ AB 交BC于点E
(2)∠ C= ∠ 1 ,∴ ∠ B= ∠C (1)四边形 ABED是平行四边形∠ B= ∠ 1 论证等腰梯形在同一底上的两个内角相等等腰梯形的性质定理:ABCD已知:在等腰梯形ABCD中,AD∥ BC,AB=DC求证: ∠ B= ∠ C , ∠ A = ∠ DEF证明:作AE⊥ BC于E,DF⊥ BC于F ABCDE 四边形ABCD是等腰梯形,延长两腰BA,
CD后交于点E,问△EBC和△EAD的形状如何?探索与研究∵四边形ABCD是等腰梯形, AD∥BC
∴ ∠ B= ∠ C ∴EB = EC∴ △EBC是等腰三角形∵ AD∥BC∴ ∠B= ∠EAD,∠C = ∠EDA∴EA = ED∴ △EAD是等腰三角形∴∠EAD = ∠EDA又∵ ∠ B= ∠ C (等腰梯形同一底上的两个内角相等)证明: △EBC和△EAD都是等腰三角形论证求证:等腰梯形的对角线相等ABCD已知:在等腰梯形ABCD中,AD ∥ BC,AB=DC12求证: AC=BD证明: ∵ ABCD是等腰梯形,AD∥BC
∴ ∠ ABC= ∠ DCB 又∵ AB=DC BC=CB∴ △ ABC≌△DCB ∴AC=BDO(OB = OC OA = OD)(等腰梯形同一条底边上的两个内角相等)1、如图:等腰梯形ABCD中,AD//BC,BA=CD,
E是AD延长线上一点,CE=CD
求证:∠B=∠E 考虑:四边形ABCE是平行四边形吗?为什么?2、如图:等腰梯形ABCD中,AD//BC,
AD=AB, BD⊥CD,
求:∠C的度数。等腰梯形中常用的添线方法作 高平移腰平移腰平移对角线延长两腰六、布置作业:
1、温习课本P93---94页;
2、学案22.5(1)
