22.4 梯形 课件(21张PPT)
图片预览






文档简介
课件21张PPT。22.4梯形060102030405梯形学习目标预习反馈新知学习当堂训练课堂小结作业布置学习目标1、理解梯形及其有关概念;
2、理解等腰梯形和直角梯形的概念;
3、 知道梯形与平行四边形的区别与联系;
4、理解梯形与三角形的联系;
5、会添加适当的辅助线将梯形问题转化成 三角形、平行四边形来解决问题;
6、会计算梯形中的有关角度、线段以及梯形的面积。
预习反馈四边形平行四边形梯形两组对边分别平行只有一组对边平行 一组对边平行而另一组对边
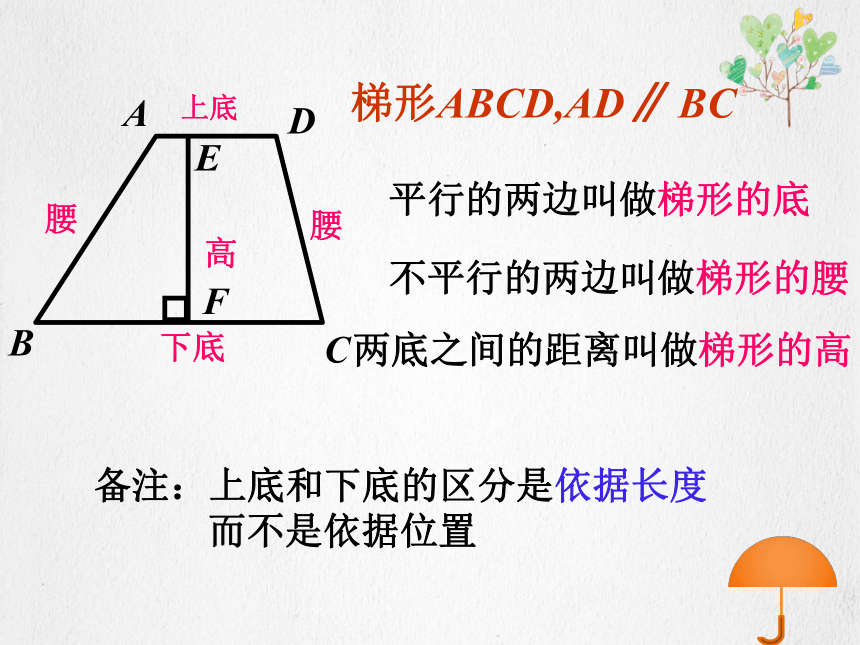
不平行的四边形叫做梯形.定义:平行的两边叫做梯形的底不平行的两边叫做梯形的腰两底之间的距离叫做梯形的高上底下底腰腰高梯形ABCD,AD∥ BC 备注:上底和下底的区分是依据长度
而不是依据位置梯形两腰相等一个角是直角等腰梯形直角梯形 1、一 组对边平行的四边形是梯形( ) 2、一组对边平行且不相等的四边形是梯形( ) 3、一组对边平行,另一组对边不平行的四边 形是梯形( ) 4、有一组对边平行,另一组对边相等的四边 形是等腰梯形( ) 5、一组对边平行而不相等,另一组对边相等 的四边形是等腰梯形( ) 6、存在既是直角梯形,又是等腰梯形的梯形 ( )判断题----概念辨析梯形与三角形的联系梯形可由三角形截得.预习反馈3、在直角梯形ABCD中,AD//BC, ∠ A=90°,
AD=10cm,DC=13cm,BC=15cm,求AB的长。作高,将梯形问题转化成直角三角形和矩形.解:作DE⊥BC于点E ,则∠DEB=90°
∵ AD//BC,
∴ ∠A+ ∠ B=180 °
∵ ∠A=90 °
∴ ∠B=90 °
∵ ∠A=90 °,∠B=90 °,∠DEB=90°
∴四边形ABED是矩形
∴AD= BE,AB=DE
∵AD=10cm,BC=15cm
∴EC=BC-BE=BC-AD=5cm
在Rt△DEC中,
∵ ∠DEC=90°
∴
∴AB=12cm
新知学习例题1:如图,在梯形ABCD中,AB//CD,
∠D=2 ∠B,AD=10,AB=15,求CD的长。平移一腰,将梯形问题转化成三角形和
平行四边形.解:作CE //DA交AB于点E
∵ AB//DC, CE //DA
∴四边形AECD是平行四边形
∴CE=DA, DC=AE, ∠D= ∠ 1
∵AD=10 ,∠D= 2∠ B
∴CE=10, ∠1= 2∠ B
∵ ∠1= ∠ B+ ∠ 2
∴∠2= ∠ B
∴EB= EC=10
∵AB=15
∴AE=AB-EB=5
∴CD=5
E12新知学习例题2:如图,在梯形ABCD中,AD//BC,
∠B=60°, ∠C=30°, AD=2厘米,
BC=8厘米,求梯形ABCD的面积。作高,将梯形问题转化成两个直角三角形和矩形.新知学习变式一:如图,在梯形ABCD中,AD//BC,
∠B=60°, ∠C=30°,点M、N分别是BC、AD的中点,求证:平移两腰,将梯形问题转化成三角形和平行四边形.EF新知学习变式二:如图,在梯形ABCD中,AD//BC,
∠B= , ∠C= ,点M、N分别是BC、AD的中点,求证:新知学习例题3(能力提升):如图,在梯形ABCD中,AD//BC, DE ⊥BC于点E,DE=4,BD=5,AC= ,求梯形ABCD的面积。平移对角线,将梯形问题转化成三角形和平行四边形.F解:作DF //AC交BC的延长线于点F新知学习例题4 (能力提升) :如图,在梯形ABCD中,AD//BC , E 为CD的中点,设△ABE的面积为S1 ,梯形ABCD的面积为S2 ,求S1 与S2 的关系.平移底,将梯形问题转化成三角形.F解:延长AE交BC的延长线于点F当堂训练练习册22.4
课堂小结课堂小结作高延长腰平移腰平移底平移对角线布置作业1、补完课堂例题格式书写;
2、《欣竹》22.4二星4、5;三星1、3、4
个性化作业
1、用1、4、4、5的线段为四边作梯形,
求这个梯形的面积.
2、已知梯形ABCD的上底AD=a,下底BC=b,
高为h,用多种方法证明:梯形的面积公式
2、理解等腰梯形和直角梯形的概念;
3、 知道梯形与平行四边形的区别与联系;
4、理解梯形与三角形的联系;
5、会添加适当的辅助线将梯形问题转化成 三角形、平行四边形来解决问题;
6、会计算梯形中的有关角度、线段以及梯形的面积。
预习反馈四边形平行四边形梯形两组对边分别平行只有一组对边平行 一组对边平行而另一组对边
不平行的四边形叫做梯形.定义:平行的两边叫做梯形的底不平行的两边叫做梯形的腰两底之间的距离叫做梯形的高上底下底腰腰高梯形ABCD,AD∥ BC 备注:上底和下底的区分是依据长度
而不是依据位置梯形两腰相等一个角是直角等腰梯形直角梯形 1、一 组对边平行的四边形是梯形( ) 2、一组对边平行且不相等的四边形是梯形( ) 3、一组对边平行,另一组对边不平行的四边 形是梯形( ) 4、有一组对边平行,另一组对边相等的四边 形是等腰梯形( ) 5、一组对边平行而不相等,另一组对边相等 的四边形是等腰梯形( ) 6、存在既是直角梯形,又是等腰梯形的梯形 ( )判断题----概念辨析梯形与三角形的联系梯形可由三角形截得.预习反馈3、在直角梯形ABCD中,AD//BC, ∠ A=90°,
AD=10cm,DC=13cm,BC=15cm,求AB的长。作高,将梯形问题转化成直角三角形和矩形.解:作DE⊥BC于点E ,则∠DEB=90°
∵ AD//BC,
∴ ∠A+ ∠ B=180 °
∵ ∠A=90 °
∴ ∠B=90 °
∵ ∠A=90 °,∠B=90 °,∠DEB=90°
∴四边形ABED是矩形
∴AD= BE,AB=DE
∵AD=10cm,BC=15cm
∴EC=BC-BE=BC-AD=5cm
在Rt△DEC中,
∵ ∠DEC=90°
∴
∴AB=12cm
新知学习例题1:如图,在梯形ABCD中,AB//CD,
∠D=2 ∠B,AD=10,AB=15,求CD的长。平移一腰,将梯形问题转化成三角形和
平行四边形.解:作CE //DA交AB于点E
∵ AB//DC, CE //DA
∴四边形AECD是平行四边形
∴CE=DA, DC=AE, ∠D= ∠ 1
∵AD=10 ,∠D= 2∠ B
∴CE=10, ∠1= 2∠ B
∵ ∠1= ∠ B+ ∠ 2
∴∠2= ∠ B
∴EB= EC=10
∵AB=15
∴AE=AB-EB=5
∴CD=5
E12新知学习例题2:如图,在梯形ABCD中,AD//BC,
∠B=60°, ∠C=30°, AD=2厘米,
BC=8厘米,求梯形ABCD的面积。作高,将梯形问题转化成两个直角三角形和矩形.新知学习变式一:如图,在梯形ABCD中,AD//BC,
∠B=60°, ∠C=30°,点M、N分别是BC、AD的中点,求证:平移两腰,将梯形问题转化成三角形和平行四边形.EF新知学习变式二:如图,在梯形ABCD中,AD//BC,
∠B= , ∠C= ,点M、N分别是BC、AD的中点,求证:新知学习例题3(能力提升):如图,在梯形ABCD中,AD//BC, DE ⊥BC于点E,DE=4,BD=5,AC= ,求梯形ABCD的面积。平移对角线,将梯形问题转化成三角形和平行四边形.F解:作DF //AC交BC的延长线于点F新知学习例题4 (能力提升) :如图,在梯形ABCD中,AD//BC , E 为CD的中点,设△ABE的面积为S1 ,梯形ABCD的面积为S2 ,求S1 与S2 的关系.平移底,将梯形问题转化成三角形.F解:延长AE交BC的延长线于点F当堂训练练习册22.4
课堂小结课堂小结作高延长腰平移腰平移底平移对角线布置作业1、补完课堂例题格式书写;
2、《欣竹》22.4二星4、5;三星1、3、4
个性化作业
1、用1、4、4、5的线段为四边作梯形,
求这个梯形的面积.
2、已知梯形ABCD的上底AD=a,下底BC=b,
高为h,用多种方法证明:梯形的面积公式
