22.5(1)等腰梯形的性质 课件(17张)
文档属性
| 名称 | 22.5(1)等腰梯形的性质 课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 272.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览

文档简介
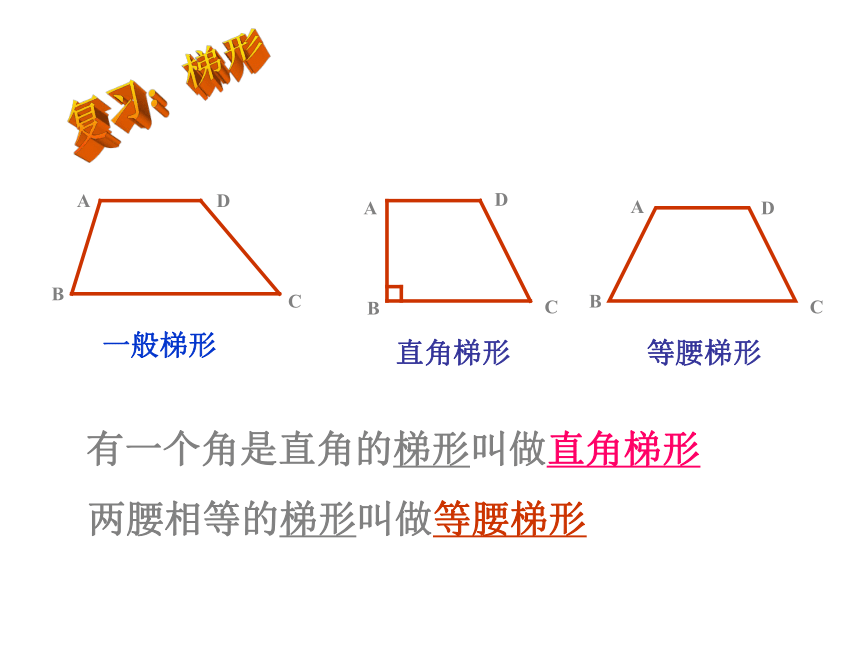
课件17张PPT。22.5(1) 等腰梯形一般梯形直角梯形等腰梯形有一个角是直角的梯形叫做直角梯形两腰相等的梯形叫做等腰梯形复习:梯形 ABCD ABCCD
A
BD
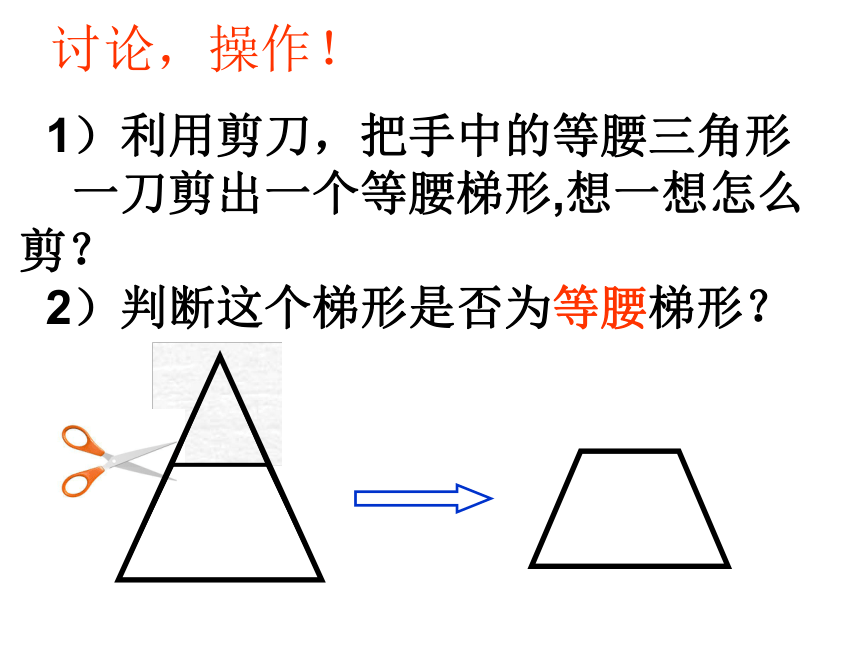
1)利用剪刀,把手中的等腰三角形
一刀剪出一个等腰梯形,想一想怎么 剪?
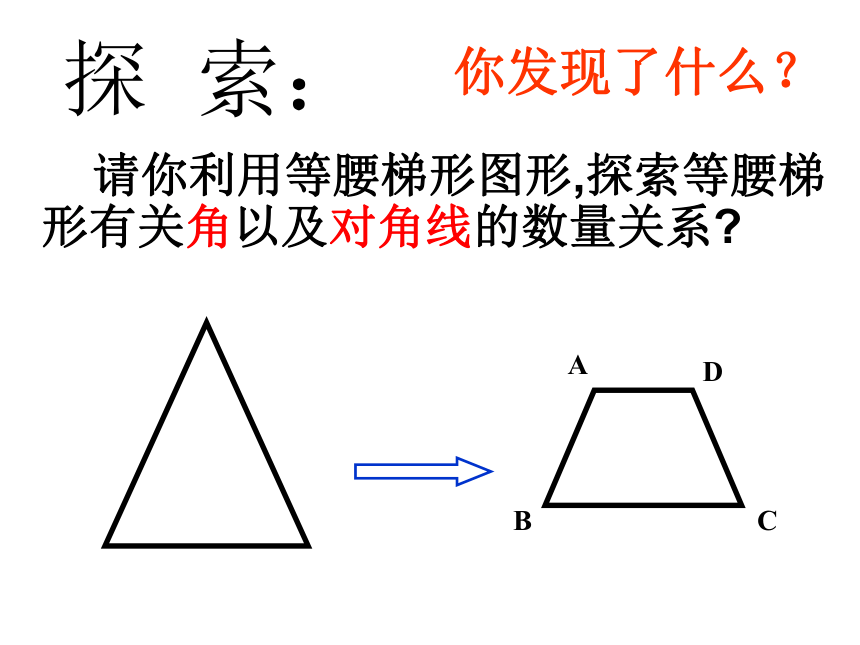
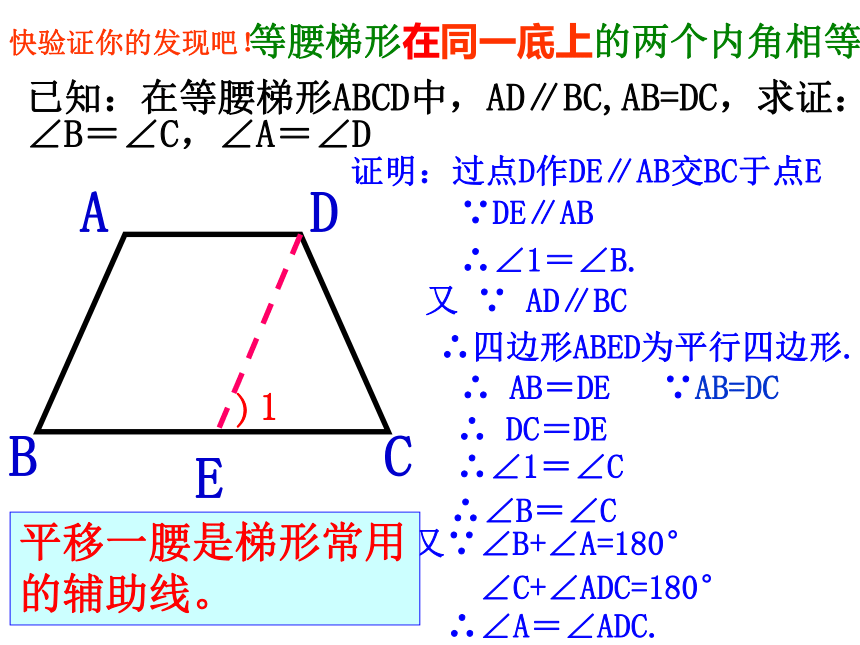
2)判断这个梯形是否为等腰梯形?讨论,操作!探 索: 请你利用等腰梯形图形,探索等腰梯形有关角以及对角线的数量关系?ABCD你发现了什么?已知:在等腰梯形ABCD中,AD∥BC,AB=DC,求证:∠B=∠C,∠A=∠D证明:过点D作DE∥AB交BC于点E ∵DE∥AB ∴∠1=∠B. 又 ∵ AD∥BC ∴四边形ABED为平行四边形. ∴ AB=DE ∵AB=DC ∴ DC=DE ∴∠1=∠C ∴∠B=∠C又∵∠B+∠A=180°
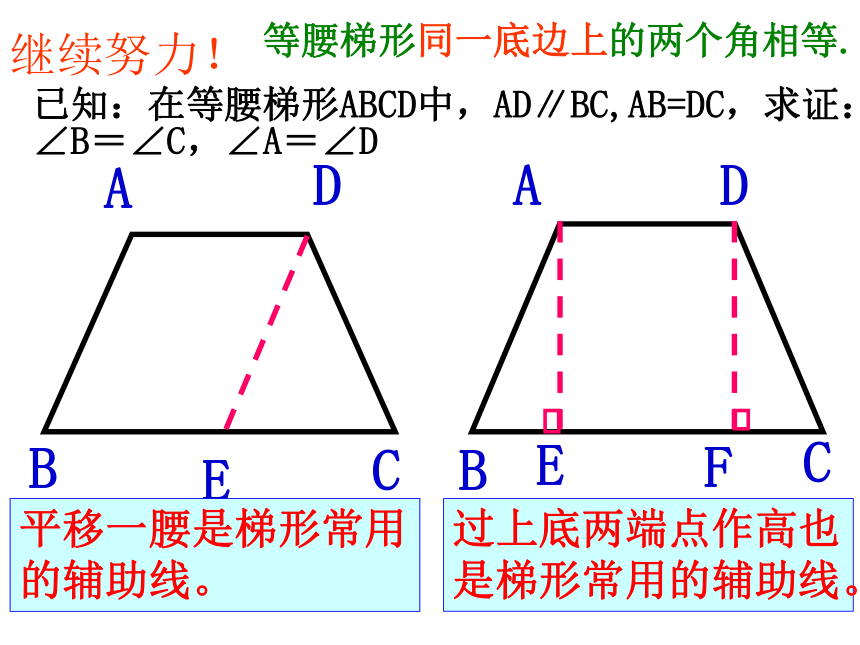
∠C+∠ADC=180°∴∠A=∠ADC.平移一腰是梯形常用的辅助线。等腰梯形在同一底上的两个内角相等.快验证你的发现吧!ABCD1)BADC过点A作AE⊥BC于点E
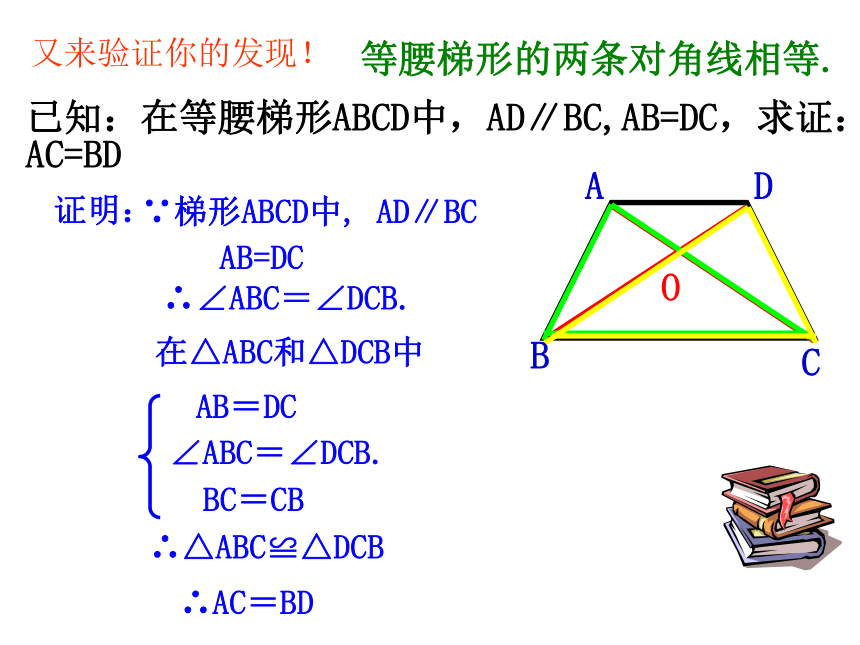
过点D作DF⊥BC于点F已知:在等腰梯形ABCD中,AD∥BC,AB=DC,求证:∠B=∠C,∠A=∠D平移一腰是梯形常用的辅助线。过上底两端点作高也是梯形常用的辅助线。等腰梯形同一底边上的两个角相等.继续努力!等腰梯形的两条对角线相等.已知:在等腰梯形ABCD中,AD∥BC,AB=DC,求证:AC=BD证明: ∵梯形ABCD中, AD∥BC ∴∠ABC=∠DCB. AB=DC 在△ABC和△DCB中 AB=DC BC=CB ∴AC=BD ∠ABC=∠DCB. ∴△ABC≌△DCB 又来验证你的发现!O 如图,四边形ABCD是等腰梯形,腰AB=DC,AC、BD是它的对角线,它是轴对称图形吗?对称轴在哪里?你能发现哪些相等的线段和相等的角?等腰梯形是轴对称图形,上下底的中点的连线所在的直线是它的对称轴。两条对角线相等两底平行,两腰相等同一底上的两个内角相等加油,成功在等你!1、如图,梯形ABCD中,AD∥BC,
AB=DC,则∠A= ,∠C= 。
2、如图,梯形ABCD中,AD∥BC,
∠A:∠B=3:1,则∠A= 度。第1,2题图第3题图4、如图,在梯形ABCD中,AD∥BC,
∠B=90°,∠C=30°,则∠A= ° ,
∠D= °
5、已知等腰梯形的一个内角等于70°,
则其他三个内角的度数是 。3、如图,梯形ABCD中,AD∥BC,
AB=DC,若AC=3cm,则BD= cm做一做∠D∠B135390150110°,110 °,70 ° 例1.如图,延长等腰梯形ABCD的两腰BA与CD,相交于点E.试说明△EBC和△EAD都是等腰三角形.解:在等腰梯形ABCD中,∠B=∠C∴EB=EC∴△EBC是等腰三角形.又∵AD//BC∴ ∠1=∠B, ∠2=∠C
∴△EAD是等腰三角形.知识应用)12(∴∠1= ∠2精讲点拨:在等腰梯形ABCD中,AD∥BC,∠B=60°,AD=15,AB=20,求BC的长。
解: 如图,分别延长BA,CD交于点E。
∵四边形ABCD是等腰梯形,且AD∥BC,
∴∠B=∠C=∠EAD=∠EDA=600.
∴EA=ED,EB=EC.
∴△EAD与△EBC都是等边三角形.
∴BC=BE=BA+AE=BA+AD=20+15=35.
变式训练:
你还有其他添加辅助线的方法,求出BC的长吗?
BCADE在等腰梯形ABCD中,AD∥BC,∠B=60°,AD=15,AB=20,求BC的长。
方法二:过D作DE ∥BC交BC于点E.
DBCAE1y练习 如图:已知在等腰梯形ABCD中, AD ∥ BC,
AB=DC,对角线AC⊥ BD,垂足为O,AD = 5
BC = 9,求梯形ABCD的面积。 ABCDO59xxy练习 如图:已知在等腰梯形ABCD中, AD ∥ BC,
AB=DC,对角线AC⊥ BD,垂足为O,AD = 5
BC = 9,求梯形ABCD的面积。 ABCDO59E△ BAD≌△DCE 梯形ABCD的面积= △BDE的面积57学习了本节课,你有什么收获?等腰梯形的性质(从“边,角,对角线,对称性”考虑)(1)两底平行,两腰相等
AD∥BC, AB=CD(2)同一底上两个内角相等
∠A= ∠D, ∠B= ∠C(3)两条对角线相等 AC=BD(4)是轴对称图形
对称轴是上(下)底的中垂线方法比知识更重要2.解决梯形问题的基本思路和方法:
通过添加适当的辅助线,把梯形问题转化为平行四边形和三角形的问题来解决。
3.常画的辅助线有以下几种:
平移一腰 作高延长两腰平移对角线再见作业:习题22.5(1)
A
BD
1)利用剪刀,把手中的等腰三角形
一刀剪出一个等腰梯形,想一想怎么 剪?
2)判断这个梯形是否为等腰梯形?讨论,操作!探 索: 请你利用等腰梯形图形,探索等腰梯形有关角以及对角线的数量关系?ABCD你发现了什么?已知:在等腰梯形ABCD中,AD∥BC,AB=DC,求证:∠B=∠C,∠A=∠D证明:过点D作DE∥AB交BC于点E ∵DE∥AB ∴∠1=∠B. 又 ∵ AD∥BC ∴四边形ABED为平行四边形. ∴ AB=DE ∵AB=DC ∴ DC=DE ∴∠1=∠C ∴∠B=∠C又∵∠B+∠A=180°
∠C+∠ADC=180°∴∠A=∠ADC.平移一腰是梯形常用的辅助线。等腰梯形在同一底上的两个内角相等.快验证你的发现吧!ABCD1)BADC过点A作AE⊥BC于点E
过点D作DF⊥BC于点F已知:在等腰梯形ABCD中,AD∥BC,AB=DC,求证:∠B=∠C,∠A=∠D平移一腰是梯形常用的辅助线。过上底两端点作高也是梯形常用的辅助线。等腰梯形同一底边上的两个角相等.继续努力!等腰梯形的两条对角线相等.已知:在等腰梯形ABCD中,AD∥BC,AB=DC,求证:AC=BD证明: ∵梯形ABCD中, AD∥BC ∴∠ABC=∠DCB. AB=DC 在△ABC和△DCB中 AB=DC BC=CB ∴AC=BD ∠ABC=∠DCB. ∴△ABC≌△DCB 又来验证你的发现!O 如图,四边形ABCD是等腰梯形,腰AB=DC,AC、BD是它的对角线,它是轴对称图形吗?对称轴在哪里?你能发现哪些相等的线段和相等的角?等腰梯形是轴对称图形,上下底的中点的连线所在的直线是它的对称轴。两条对角线相等两底平行,两腰相等同一底上的两个内角相等加油,成功在等你!1、如图,梯形ABCD中,AD∥BC,
AB=DC,则∠A= ,∠C= 。
2、如图,梯形ABCD中,AD∥BC,
∠A:∠B=3:1,则∠A= 度。第1,2题图第3题图4、如图,在梯形ABCD中,AD∥BC,
∠B=90°,∠C=30°,则∠A= ° ,
∠D= °
5、已知等腰梯形的一个内角等于70°,
则其他三个内角的度数是 。3、如图,梯形ABCD中,AD∥BC,
AB=DC,若AC=3cm,则BD= cm做一做∠D∠B135390150110°,110 °,70 ° 例1.如图,延长等腰梯形ABCD的两腰BA与CD,相交于点E.试说明△EBC和△EAD都是等腰三角形.解:在等腰梯形ABCD中,∠B=∠C∴EB=EC∴△EBC是等腰三角形.又∵AD//BC∴ ∠1=∠B, ∠2=∠C
∴△EAD是等腰三角形.知识应用)12(∴∠1= ∠2精讲点拨:在等腰梯形ABCD中,AD∥BC,∠B=60°,AD=15,AB=20,求BC的长。
解: 如图,分别延长BA,CD交于点E。
∵四边形ABCD是等腰梯形,且AD∥BC,
∴∠B=∠C=∠EAD=∠EDA=600.
∴EA=ED,EB=EC.
∴△EAD与△EBC都是等边三角形.
∴BC=BE=BA+AE=BA+AD=20+15=35.
变式训练:
你还有其他添加辅助线的方法,求出BC的长吗?
BCADE在等腰梯形ABCD中,AD∥BC,∠B=60°,AD=15,AB=20,求BC的长。
方法二:过D作DE ∥BC交BC于点E.
DBCAE1y练习 如图:已知在等腰梯形ABCD中, AD ∥ BC,
AB=DC,对角线AC⊥ BD,垂足为O,AD = 5
BC = 9,求梯形ABCD的面积。 ABCDO59xxy练习 如图:已知在等腰梯形ABCD中, AD ∥ BC,
AB=DC,对角线AC⊥ BD,垂足为O,AD = 5
BC = 9,求梯形ABCD的面积。 ABCDO59E△ BAD≌△DCE 梯形ABCD的面积= △BDE的面积57学习了本节课,你有什么收获?等腰梯形的性质(从“边,角,对角线,对称性”考虑)(1)两底平行,两腰相等
AD∥BC, AB=CD(2)同一底上两个内角相等
∠A= ∠D, ∠B= ∠C(3)两条对角线相等 AC=BD(4)是轴对称图形
对称轴是上(下)底的中垂线方法比知识更重要2.解决梯形问题的基本思路和方法:
通过添加适当的辅助线,把梯形问题转化为平行四边形和三角形的问题来解决。
3.常画的辅助线有以下几种:
平移一腰 作高延长两腰平移对角线再见作业:习题22.5(1)
