22.5(1)等腰梯形的性质 课件(17张PPT)
文档属性
| 名称 | 22.5(1)等腰梯形的性质 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 104.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览


文档简介
课件17张PPT。22.5(1) 等腰梯形的性质一、巩固旧知、引出新知口答:
(1) 什么叫梯形?
(2) 什么叫等腰梯形?
(3)等腰梯形的表达式:
等腰梯形有哪些性质?二、验证猜想、形成定理 1.从边来考虑:根据等腰梯形的定义具有___________________ 两腰相等、底边互相平行二、验证猜想、形成定理 2.从角考虑:猜一猜?
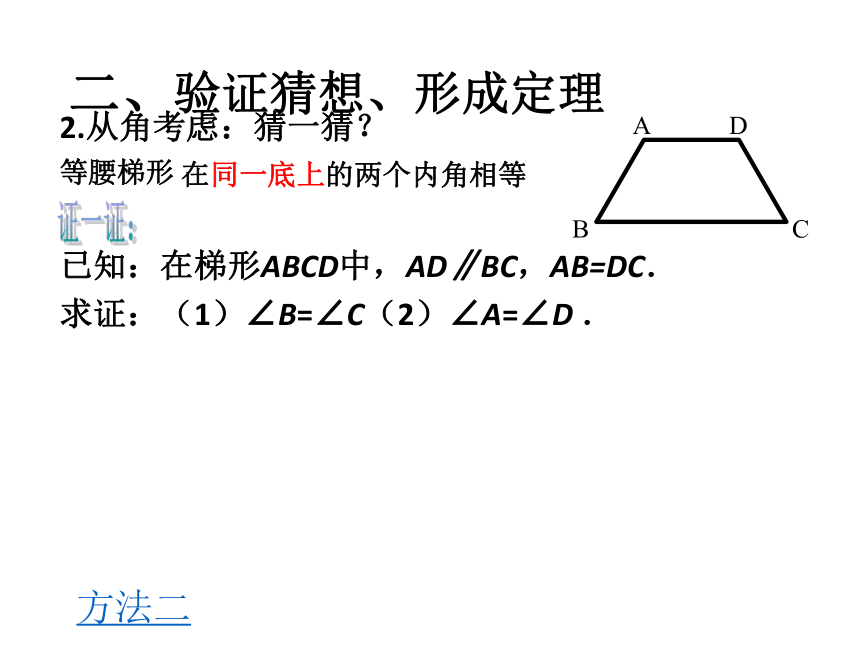
等腰梯形
已知:在梯形ABCD中,AD∥BC,AB=DC.
求证:(1)∠B=∠C(2)∠A=∠D .证一证:在同一底上的两个内角相等方法二二、验证猜想、形成定理 已知:梯形ABCD,AD∥BC,AB=DC.
求证:(1)∠B=∠C(2)∠A=∠D .下一页证明:(1)过点A作AE⊥BC,垂足为E;
过点D作DF⊥BC,垂足为F
则∠AEB= ∠DFC=90°又∵ AD∥BC
∴ AE= DF(平行线间的距离
处处相等)∵ AB=DC
∴ Rt △ABE≌Rt △ DCF (HL)
∴ ∠ B= ∠ C (2) ∵ AD∥BC
∴ ∠B+ ∠BAD=180°
∠C+ ∠ADC=180°
又∵ ∠B= ∠C
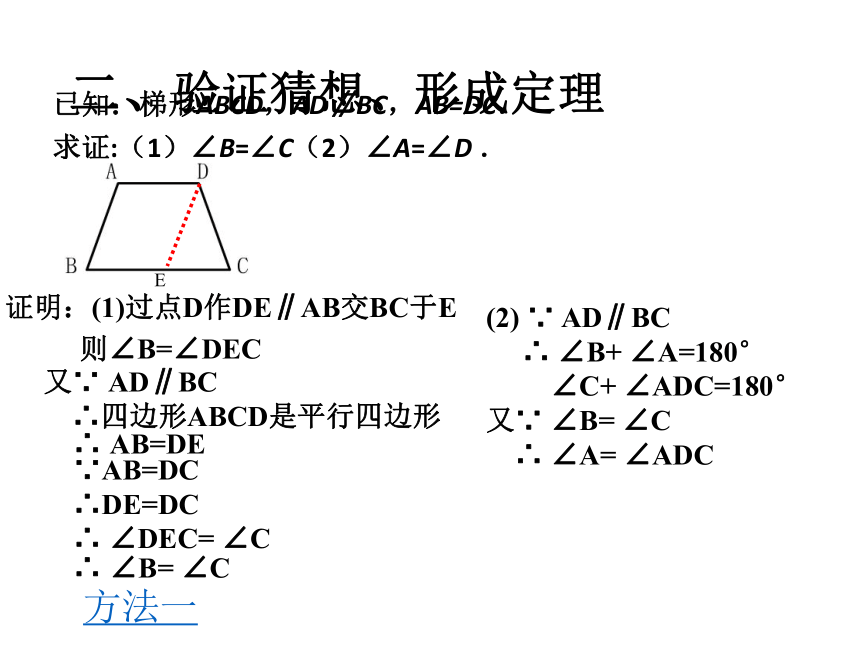
∴ ∠BAD= ∠ADC二、验证猜想、形成定理 已知:梯形ABCD,AD∥BC,AB=DC.
求证:(1)∠B=∠C(2)∠A=∠D .方法一证明:(1)过点D作DE∥AB交BC于E则∠B=∠DEC又∵ AD∥BC
∴四边形ABCD是平行四边形∴ AB=DE∵AB=DC
∴DE=DC
∴ ∠DEC= ∠C∴ ∠B= ∠C(2) ∵ AD∥BC
∴ ∠B+ ∠A=180°
∠C+ ∠ADC=180°
又∵ ∠B= ∠C
∴ ∠A= ∠ADC二、验证猜想、形成定理等腰梯形性质定理1:
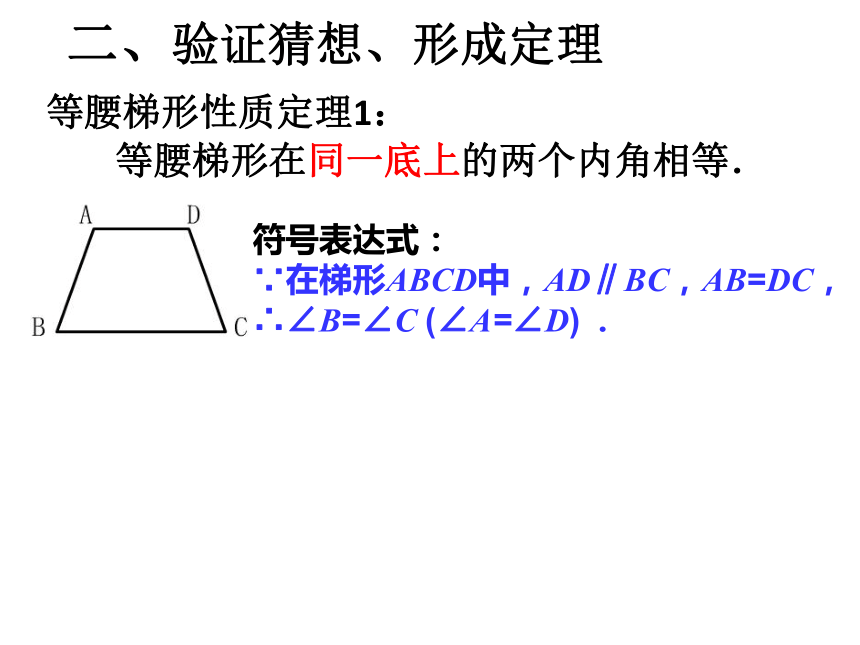
等腰梯形在同一底上的两个内角相等.
符号表达式:
∵在梯形ABCD中,AD∥BC,AB=DC,
∴∠B=∠C (∠A=∠D) . 二、验证猜想、形成定理从对角线考虑:
猜一猜:等腰梯形的两条对角线_____证一证:已知:在梯形ABCD中,AD∥BC,AB=DC.
求证:AC=DB.相等二、验证猜想、形成定理等腰梯形性质定理2:
等腰梯形的两条对角线相等.
符号表达式:
∵在梯形ABCD中,AD∥BC,AB=DC,
∴AC=DB. o三、应用定理、深化认知例1 .已知:如图,等腰梯形ABCD中,AD∥BC,腰BA和CD的延长线
相交于点E.
求证:⊿EAD是等腰三角形.作∠BEC的平分线,交AD于M,交BC于N,则它既垂直平分AD,又垂直平分BC
即∠BEC的平分线所在的直线经过AD的中点M和BC的中点N.
由等腰三角形是轴对称图形 ,
对称轴是两底的中点的连线所在的直线
因此等腰梯形也是轴对称图形.4.例题讲解,熟悉新知: 例2 .如图:等腰梯形ABCD中,AD∥ BC,AB=CD,
延长BC使CE=AD,并连接DE .
求证:BD=DE .证明:∵梯形ABCD中,AD∥ BC,AB=CD.
∴∠BAD=∠ADC
∠ADC=∠DCE
∴∠BAD =∠DCE
∵AB=CD,AD=CE
∴△ABD≌△CDE
∴BD=DE四、小结梳理、布置作业畅所欲言:谈谈你今天学到了什么四、应用定理,深化认知:1.如图,在等腰梯形ABCD,AD∥BC,AD=AB,
BD⊥DC.则∠C=______.60°四、小结梳理、布置作业2. 等腰梯形ABCD中,AD∥BC,AB=CD,∠ABC=60°,AD=15,AB=45,求BC的长 .
谢谢四、探究等腰梯形ABCD中,AD∥ BC,AB=CD,延长BC使CE=AD,并连接DE.
求证:BD=DE .
等腰梯形ABCD的面积和等腰三角形DBE的面积有什么关系?证明:∵ △ABD≌△CDE
∴S△ABD=S △CDE
相等又∵S梯形ABCD =S △ABD+S △BCD
S △ DBE =S △CDE+S △BCD ∴ S梯形ABCD = S △ DBE 变式等腰梯形ABCD中,AD∥ BC,AB=CD,AC⊥DB,AD=4,BC=6 ,求等腰梯形ABCD的面积
(1) 什么叫梯形?
(2) 什么叫等腰梯形?
(3)等腰梯形的表达式:
等腰梯形有哪些性质?二、验证猜想、形成定理 1.从边来考虑:根据等腰梯形的定义具有___________________ 两腰相等、底边互相平行二、验证猜想、形成定理 2.从角考虑:猜一猜?
等腰梯形
已知:在梯形ABCD中,AD∥BC,AB=DC.
求证:(1)∠B=∠C(2)∠A=∠D .证一证:在同一底上的两个内角相等方法二二、验证猜想、形成定理 已知:梯形ABCD,AD∥BC,AB=DC.
求证:(1)∠B=∠C(2)∠A=∠D .下一页证明:(1)过点A作AE⊥BC,垂足为E;
过点D作DF⊥BC,垂足为F
则∠AEB= ∠DFC=90°又∵ AD∥BC
∴ AE= DF(平行线间的距离
处处相等)∵ AB=DC
∴ Rt △ABE≌Rt △ DCF (HL)
∴ ∠ B= ∠ C (2) ∵ AD∥BC
∴ ∠B+ ∠BAD=180°
∠C+ ∠ADC=180°
又∵ ∠B= ∠C
∴ ∠BAD= ∠ADC二、验证猜想、形成定理 已知:梯形ABCD,AD∥BC,AB=DC.
求证:(1)∠B=∠C(2)∠A=∠D .方法一证明:(1)过点D作DE∥AB交BC于E则∠B=∠DEC又∵ AD∥BC
∴四边形ABCD是平行四边形∴ AB=DE∵AB=DC
∴DE=DC
∴ ∠DEC= ∠C∴ ∠B= ∠C(2) ∵ AD∥BC
∴ ∠B+ ∠A=180°
∠C+ ∠ADC=180°
又∵ ∠B= ∠C
∴ ∠A= ∠ADC二、验证猜想、形成定理等腰梯形性质定理1:
等腰梯形在同一底上的两个内角相等.
符号表达式:
∵在梯形ABCD中,AD∥BC,AB=DC,
∴∠B=∠C (∠A=∠D) . 二、验证猜想、形成定理从对角线考虑:
猜一猜:等腰梯形的两条对角线_____证一证:已知:在梯形ABCD中,AD∥BC,AB=DC.
求证:AC=DB.相等二、验证猜想、形成定理等腰梯形性质定理2:
等腰梯形的两条对角线相等.
符号表达式:
∵在梯形ABCD中,AD∥BC,AB=DC,
∴AC=DB. o三、应用定理、深化认知例1 .已知:如图,等腰梯形ABCD中,AD∥BC,腰BA和CD的延长线
相交于点E.
求证:⊿EAD是等腰三角形.作∠BEC的平分线,交AD于M,交BC于N,则它既垂直平分AD,又垂直平分BC
即∠BEC的平分线所在的直线经过AD的中点M和BC的中点N.
由等腰三角形是轴对称图形 ,
对称轴是两底的中点的连线所在的直线
因此等腰梯形也是轴对称图形.4.例题讲解,熟悉新知: 例2 .如图:等腰梯形ABCD中,AD∥ BC,AB=CD,
延长BC使CE=AD,并连接DE .
求证:BD=DE .证明:∵梯形ABCD中,AD∥ BC,AB=CD.
∴∠BAD=∠ADC
∠ADC=∠DCE
∴∠BAD =∠DCE
∵AB=CD,AD=CE
∴△ABD≌△CDE
∴BD=DE四、小结梳理、布置作业畅所欲言:谈谈你今天学到了什么四、应用定理,深化认知:1.如图,在等腰梯形ABCD,AD∥BC,AD=AB,
BD⊥DC.则∠C=______.60°四、小结梳理、布置作业2. 等腰梯形ABCD中,AD∥BC,AB=CD,∠ABC=60°,AD=15,AB=45,求BC的长 .
谢谢四、探究等腰梯形ABCD中,AD∥ BC,AB=CD,延长BC使CE=AD,并连接DE.
求证:BD=DE .
等腰梯形ABCD的面积和等腰三角形DBE的面积有什么关系?证明:∵ △ABD≌△CDE
∴S△ABD=S △CDE
相等又∵S梯形ABCD =S △ABD+S △BCD
S △ DBE =S △CDE+S △BCD ∴ S梯形ABCD = S △ DBE 变式等腰梯形ABCD中,AD∥ BC,AB=CD,AC⊥DB,AD=4,BC=6 ,求等腰梯形ABCD的面积
