22.5(1) 等腰梯形的性质 课件(15张PPT)
文档属性
| 名称 | 22.5(1) 等腰梯形的性质 课件(15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览


文档简介
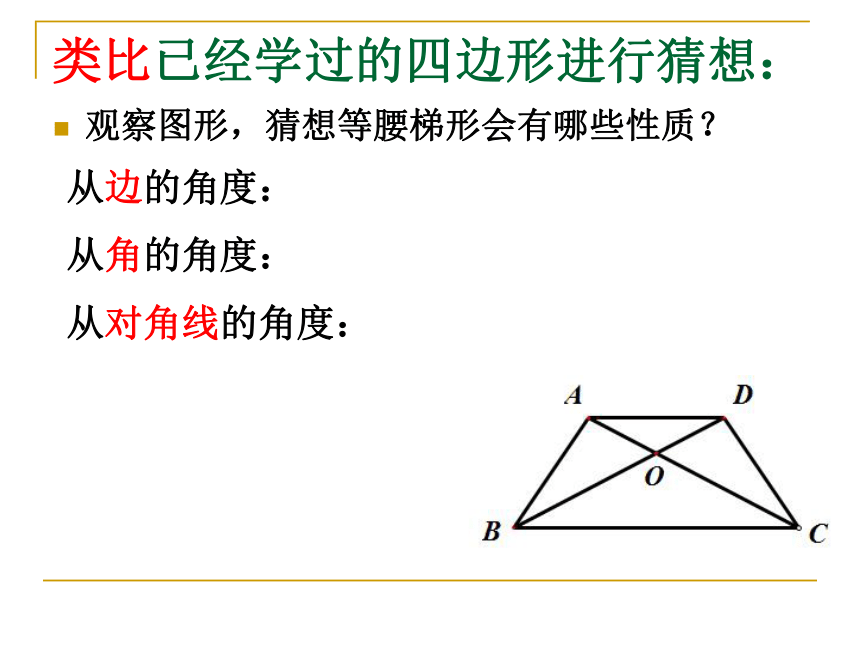
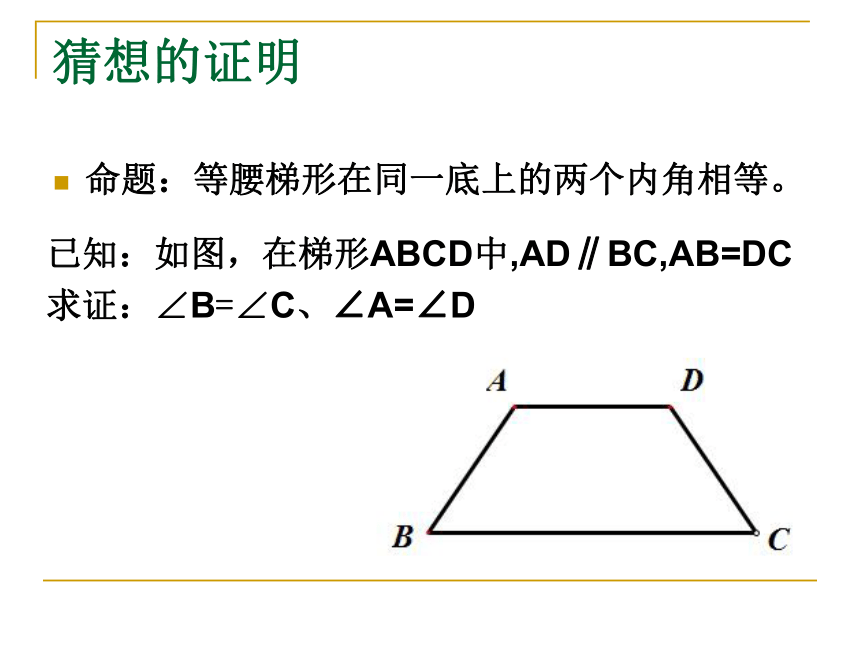
课件15张PPT。22.5(1)等腰梯形的性质等腰三角形与等腰梯形的类比两边相等的三角形叫做等腰三角形。两腰相等的梯形叫做等腰梯形。类比已经学过的四边形进行猜想:观察图形,猜想等腰梯形会有哪些性质? 从边的角度:从角的角度:从对角线的角度:猜想的证明 命题:等腰梯形在同一底上的两个内角相等。已知:如图,在梯形ABCD中,AD∥BC,AB=DC
求证:∠B=∠C、∠A=∠D 辅助线的添法——转化思想(2)过点C作CE∥AB,交AD的延长线于点E(1)过点D作DE∥AB,交BC于点E(3) 过点A作AH⊥BC,过点D作DG⊥BC,垂足分别为点H、点G 等腰梯形性质定理1等腰梯形在同一底上的两个内角相等。 符号表示为:
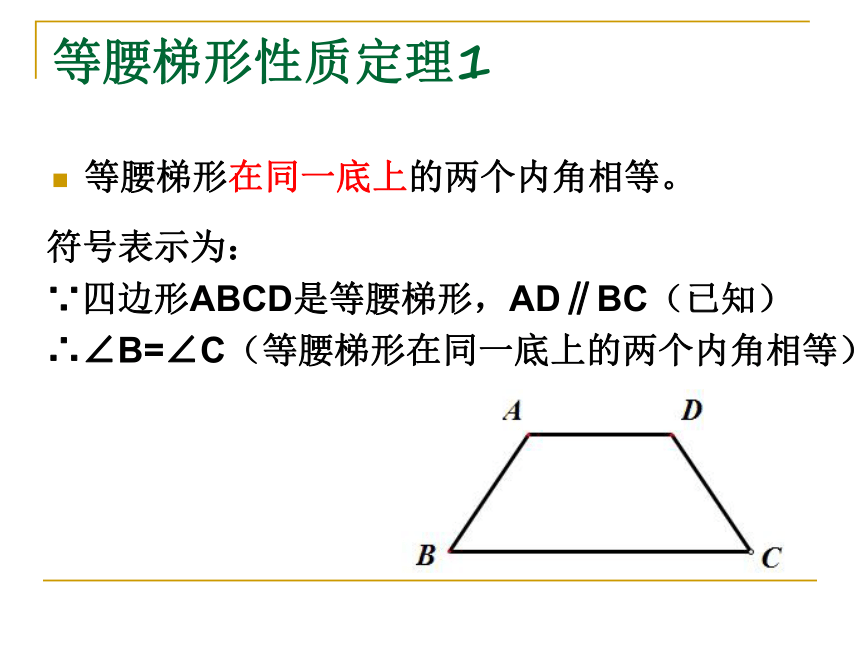
∵四边形ABCD是等腰梯形,AD∥BC(已知)
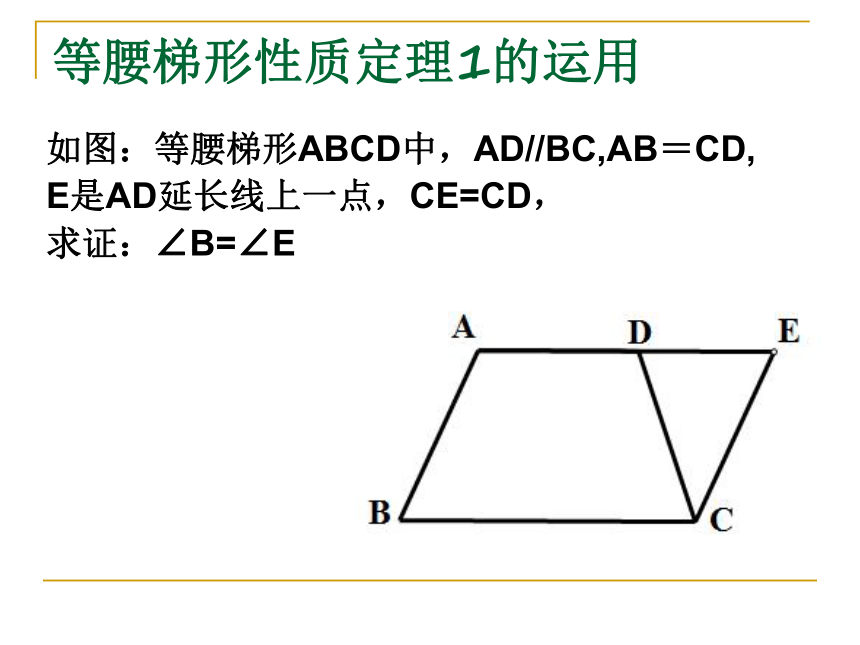
∴∠B=∠C(等腰梯形在同一底上的两个内角相等) 等腰梯形性质定理1的运用如图:等腰梯形ABCD中,AD//BC,AB=CD,
E是AD延长线上一点,CE=CD,
求证:∠B=∠E 探究等腰三角形与等腰梯形的联系 一个等腰三角形被平行于底边且与两腰相交(交点非顶点)的直线所截,截得的四边形一定是等腰梯形。那么反过来,给定一个等腰梯形,延长两腰后交于一点,得到的图形是否是等腰三角形?如图:等腰梯形ABCD中,AD//BC,腰BA和CD的延长线交于点E
求证:△EAD是等腰三角形探究等腰三角形与等腰梯形的联系 (1)图中共有几个等腰三角形?
(2)如果作∠E的平分线,它垂直平分AD吗?垂直平分BC吗?等腰三角形的对称性等腰梯形是轴对称图形,对称轴是两底的中点的连线所在的直线。 猜想的证明 命题:等腰梯形的两条对角线相等。如图,在梯形ABCD中,AD∥BC,AB=DC,对角线AC和BD相交于点O
求证:AC=BD等腰梯形性质定理2 等腰梯形的两条对角线相等。符号表示为:
∵四边形ABCD是等腰梯形,AD∥BC
∴AC=BD(等腰梯形的两条对角线相等) ,
回顾反思 布置作业 练习册 第48页 习题22.5(1)
求证:∠B=∠C、∠A=∠D 辅助线的添法——转化思想(2)过点C作CE∥AB,交AD的延长线于点E(1)过点D作DE∥AB,交BC于点E(3) 过点A作AH⊥BC,过点D作DG⊥BC,垂足分别为点H、点G 等腰梯形性质定理1等腰梯形在同一底上的两个内角相等。 符号表示为:
∵四边形ABCD是等腰梯形,AD∥BC(已知)
∴∠B=∠C(等腰梯形在同一底上的两个内角相等) 等腰梯形性质定理1的运用如图:等腰梯形ABCD中,AD//BC,AB=CD,
E是AD延长线上一点,CE=CD,
求证:∠B=∠E 探究等腰三角形与等腰梯形的联系 一个等腰三角形被平行于底边且与两腰相交(交点非顶点)的直线所截,截得的四边形一定是等腰梯形。那么反过来,给定一个等腰梯形,延长两腰后交于一点,得到的图形是否是等腰三角形?如图:等腰梯形ABCD中,AD//BC,腰BA和CD的延长线交于点E
求证:△EAD是等腰三角形探究等腰三角形与等腰梯形的联系 (1)图中共有几个等腰三角形?
(2)如果作∠E的平分线,它垂直平分AD吗?垂直平分BC吗?等腰三角形的对称性等腰梯形是轴对称图形,对称轴是两底的中点的连线所在的直线。 猜想的证明 命题:等腰梯形的两条对角线相等。如图,在梯形ABCD中,AD∥BC,AB=DC,对角线AC和BD相交于点O
求证:AC=BD等腰梯形性质定理2 等腰梯形的两条对角线相等。符号表示为:
∵四边形ABCD是等腰梯形,AD∥BC
∴AC=BD(等腰梯形的两条对角线相等) ,
回顾反思 布置作业 练习册 第48页 习题22.5(1)
