人教版七年数学下册课件 5.2.2平行线的判定(19张PPT)
文档属性
| 名称 | 人教版七年数学下册课件 5.2.2平行线的判定(19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 552.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-26 20:47:55 | ||
图片预览



文档简介
(共19张PPT)
5.2 平行线及其判定(第2课时)
人教版七年级下册
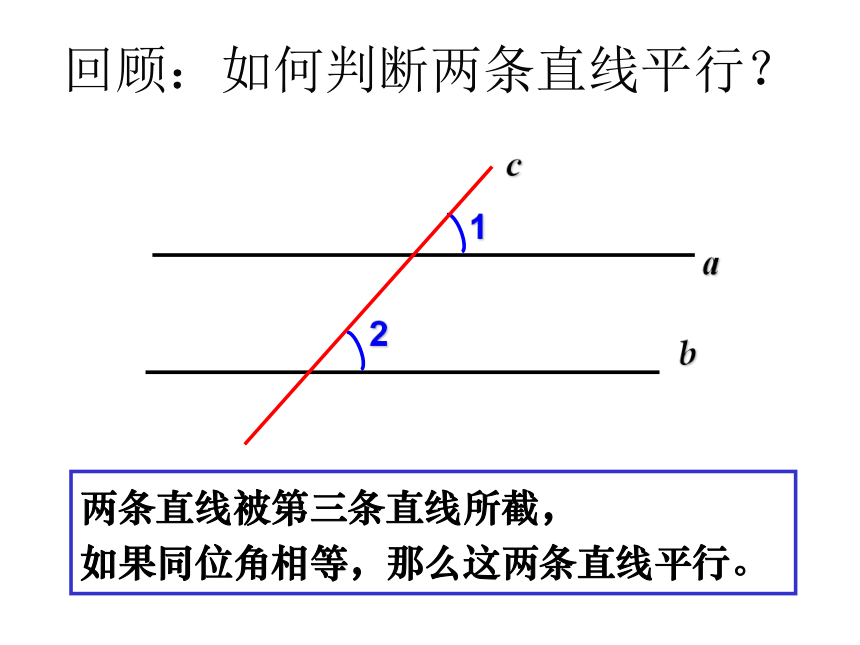
回顾:如何判断两条直线平行?
两条直线被第三条直线所截,
如果同位角相等,那么这两条直线平行。
同位角:同旁同侧
内错角:内部两旁
同旁内角:内部同旁
B
D
2
1
E
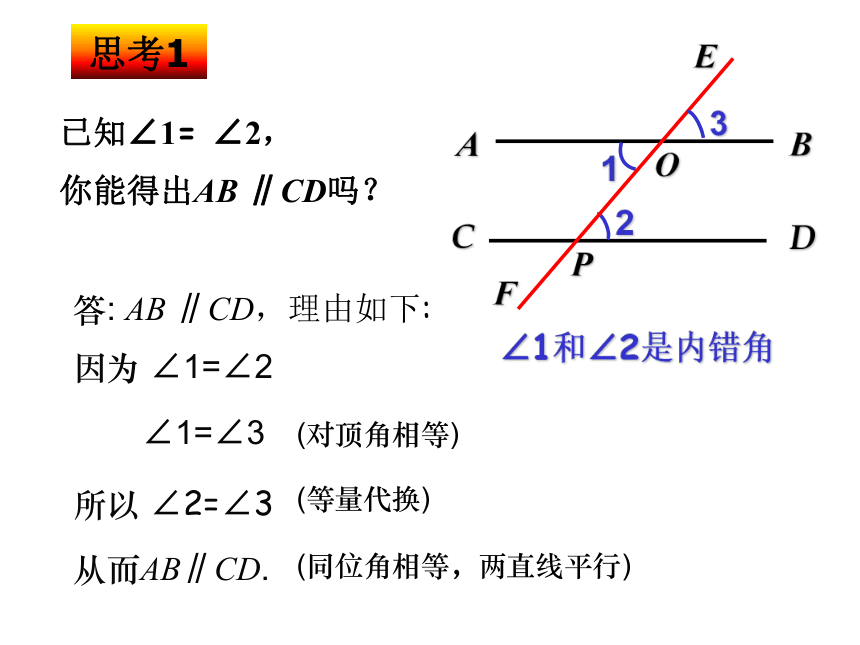
已知∠1= ∠2,
你能得出AB ∥CD吗?
A
C
F
O
P
因为 ∠1=∠2
所以 ∠2=∠3
∠1=∠3
(对顶角相等)
(等量代换)
从而AB∥CD.
(同位角相等,两直线平行)
∠1和∠2是内错角
思考1
答: AB ∥CD,理由如下:
B
D
2
1
E
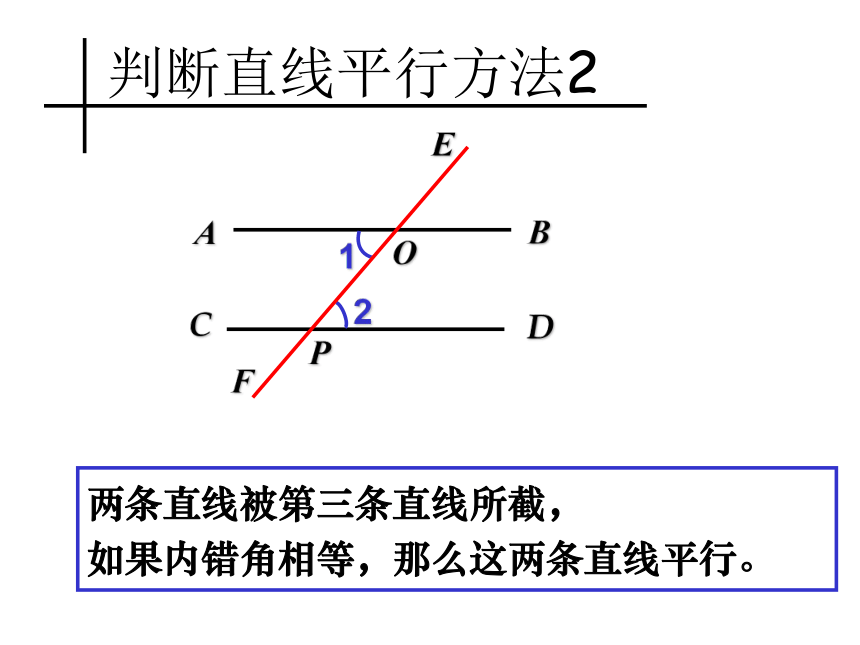
判断直线平行方法2
A
C
F
O
P
两条直线被第三条直线所截,
如果内错角相等,那么这两条直线平行。
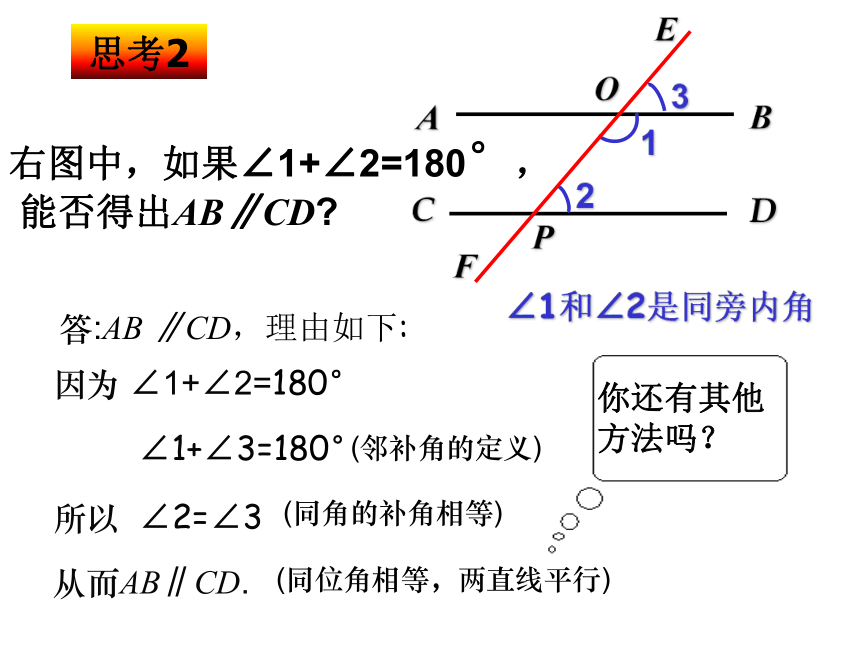
右图中,如果∠1+∠2=180°,
能否得出AB∥CD?
思考2
B
D
2
1
E
A
C
F
O
P
∠1和∠2是同旁内角
因为 ∠1+∠2=180°
所以 ∠2=∠3
∠1+∠3=180°
(邻补角的定义)
(同角的补角相等)
从而AB∥CD.
(同位角相等,两直线平行)
答:AB ∥CD,理由如下:
右图中,如果∠1+∠2=180°,
能得出AB∥CD吗?
B
D
2
1
E
A
C
F
O
P
∠1和∠2是同旁内角
因为 ∠1+∠2=180°
所以 ∠2=∠3
∠1+∠3=180°
(邻补角的定义)
(同角的补角相等)
从而AB∥CD.
(内错角相等,两直线平行)
理由:
判断直线平行方法3
两条直线被第三条直线所截,
如果同旁内角互补,那么这两条直线平行。
B
D
2
1
E
A
C
F
O
P
例1 如图, BE是AB的延长线.
(1)由∠CBE=∠A可以判定哪两 条直线平行? 根据是什么?
(2)由∠CBE=∠C可以判定哪两条直线平行? 根据是什么?
(3)由∠D+∠A= 180°可以判定哪两条直线平行?根据是什么?
(1)从∠1=∠2,可以推出 ∥ ,
理由是 。
(2)从∠2=∠ ,可以推出c∥d ,
理由是 。
(3)如果∠1=75°,∠4=105°,
可以推出 ∥ 。
理由是 。
练一练
b
a
内错角相等,两直线平行
同位角相等,两直线平行
3
c
d
4
2
c
d
3
1
a
b
同旁内角互补,两直线平行
1.如图
从∠1=∠4,可以推出 ∥ ,
理由是 。
(3)从∠ABC +∠ =180,可以推出AB∥CD ,
理由是 。
(2)从∠ =∠ ,可以推出AD∥BC,
理由是 。
(4)从∠5=∠ ,可以推出AB∥CD,
理由是 。
练一练
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
2
3
内错角相等,两直线平行
ABC
同位角相等,两直线平行
2.如图
3.两条直线垂直于同一条直线,这两条
直线平行吗?为什么?
答:垂直于同一条直线的两条直线平行.
练一练
因为 b⊥a
所以 ∠2=90°
(垂直的定义)
从而b∥c.
(同位角相等,两直线平行)
所以 ∠1=90°
(垂直的定义)
因为 c ⊥a
所以 ∠1=∠2
(等量代换)
解法1:
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)
a
b
c
1
2
解法2:
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)
a
b
c
1
2
解法3:
结论
如果两条直线都垂直于同一条直线,
那么这两条直线平行。
b
c
a
提高题:
如图,直线a,b,c被m所截,∠1=∠2,∠1=∠3
请问:a,c相互平行吗?试着说明理由.
通过这节课的学习,
你有哪些收获?
议一议
1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5.如果两条直线都与第三条直线垂直,
那么这两条直线也互相平行.
判定两条直线是否平行的方法有:
5.2 平行线及其判定(第2课时)
人教版七年级下册
回顾:如何判断两条直线平行?
两条直线被第三条直线所截,
如果同位角相等,那么这两条直线平行。
同位角:同旁同侧
内错角:内部两旁
同旁内角:内部同旁
B
D
2
1
E
已知∠1= ∠2,
你能得出AB ∥CD吗?
A
C
F
O
P
因为 ∠1=∠2
所以 ∠2=∠3
∠1=∠3
(对顶角相等)
(等量代换)
从而AB∥CD.
(同位角相等,两直线平行)
∠1和∠2是内错角
思考1
答: AB ∥CD,理由如下:
B
D
2
1
E
判断直线平行方法2
A
C
F
O
P
两条直线被第三条直线所截,
如果内错角相等,那么这两条直线平行。
右图中,如果∠1+∠2=180°,
能否得出AB∥CD?
思考2
B
D
2
1
E
A
C
F
O
P
∠1和∠2是同旁内角
因为 ∠1+∠2=180°
所以 ∠2=∠3
∠1+∠3=180°
(邻补角的定义)
(同角的补角相等)
从而AB∥CD.
(同位角相等,两直线平行)
答:AB ∥CD,理由如下:
右图中,如果∠1+∠2=180°,
能得出AB∥CD吗?
B
D
2
1
E
A
C
F
O
P
∠1和∠2是同旁内角
因为 ∠1+∠2=180°
所以 ∠2=∠3
∠1+∠3=180°
(邻补角的定义)
(同角的补角相等)
从而AB∥CD.
(内错角相等,两直线平行)
理由:
判断直线平行方法3
两条直线被第三条直线所截,
如果同旁内角互补,那么这两条直线平行。
B
D
2
1
E
A
C
F
O
P
例1 如图, BE是AB的延长线.
(1)由∠CBE=∠A可以判定哪两 条直线平行? 根据是什么?
(2)由∠CBE=∠C可以判定哪两条直线平行? 根据是什么?
(3)由∠D+∠A= 180°可以判定哪两条直线平行?根据是什么?
(1)从∠1=∠2,可以推出 ∥ ,
理由是 。
(2)从∠2=∠ ,可以推出c∥d ,
理由是 。
(3)如果∠1=75°,∠4=105°,
可以推出 ∥ 。
理由是 。
练一练
b
a
内错角相等,两直线平行
同位角相等,两直线平行
3
c
d
4
2
c
d
3
1
a
b
同旁内角互补,两直线平行
1.如图
从∠1=∠4,可以推出 ∥ ,
理由是 。
(3)从∠ABC +∠ =180,可以推出AB∥CD ,
理由是 。
(2)从∠ =∠ ,可以推出AD∥BC,
理由是 。
(4)从∠5=∠ ,可以推出AB∥CD,
理由是 。
练一练
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
2
3
内错角相等,两直线平行
ABC
同位角相等,两直线平行
2.如图
3.两条直线垂直于同一条直线,这两条
直线平行吗?为什么?
答:垂直于同一条直线的两条直线平行.
练一练
因为 b⊥a
所以 ∠2=90°
(垂直的定义)
从而b∥c.
(同位角相等,两直线平行)
所以 ∠1=90°
(垂直的定义)
因为 c ⊥a
所以 ∠1=∠2
(等量代换)
解法1:
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)
a
b
c
1
2
解法2:
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)
a
b
c
1
2
解法3:
结论
如果两条直线都垂直于同一条直线,
那么这两条直线平行。
b
c
a
提高题:
如图,直线a,b,c被m所截,∠1=∠2,∠1=∠3
请问:a,c相互平行吗?试着说明理由.
通过这节课的学习,
你有哪些收获?
议一议
1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5.如果两条直线都与第三条直线垂直,
那么这两条直线也互相平行.
判定两条直线是否平行的方法有:
