22.6(1) 三角形的中位线 课件(25张PPT)
文档属性
| 名称 | 22.6(1) 三角形的中位线 课件(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 465.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 00:00:00 | ||
图片预览


文档简介
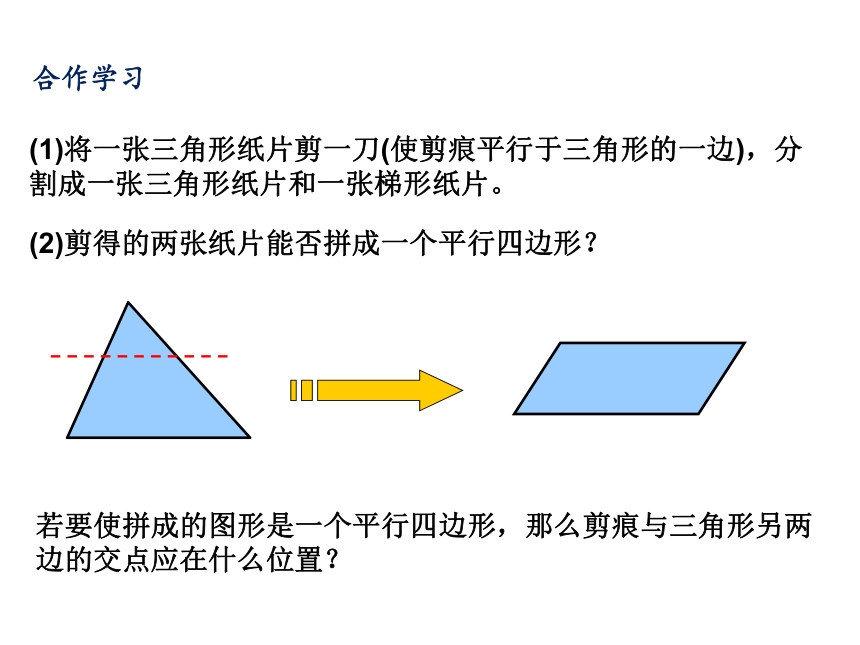
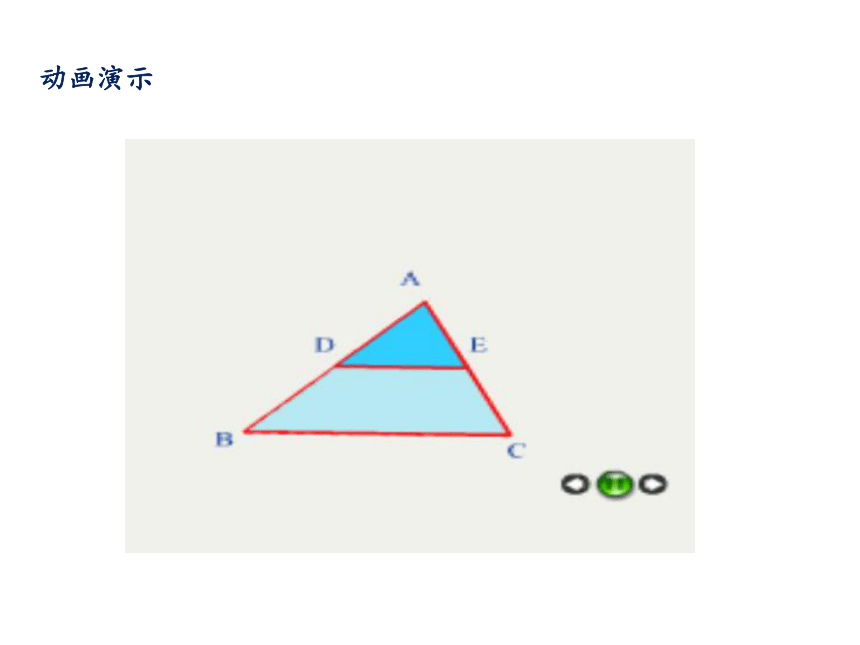
课件25张PPT。22.6(1)三角形中位线合作学习(1)将一张三角形纸片剪一刀(使剪痕平行于三角形的一边),分割成一张三角形纸片和一张梯形纸片。(2)剪得的两张纸片能否拼成一个平行四边形?若要使拼成的图形是一个平行四边形,那么剪痕与三角形另两边的交点应在什么位置?动画演示定义:联结三角形两边中点的
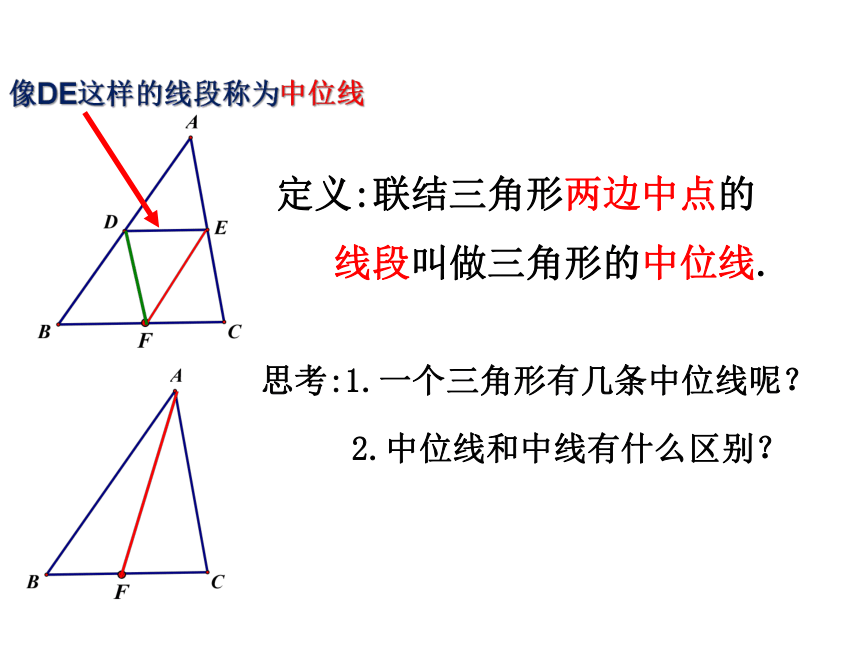
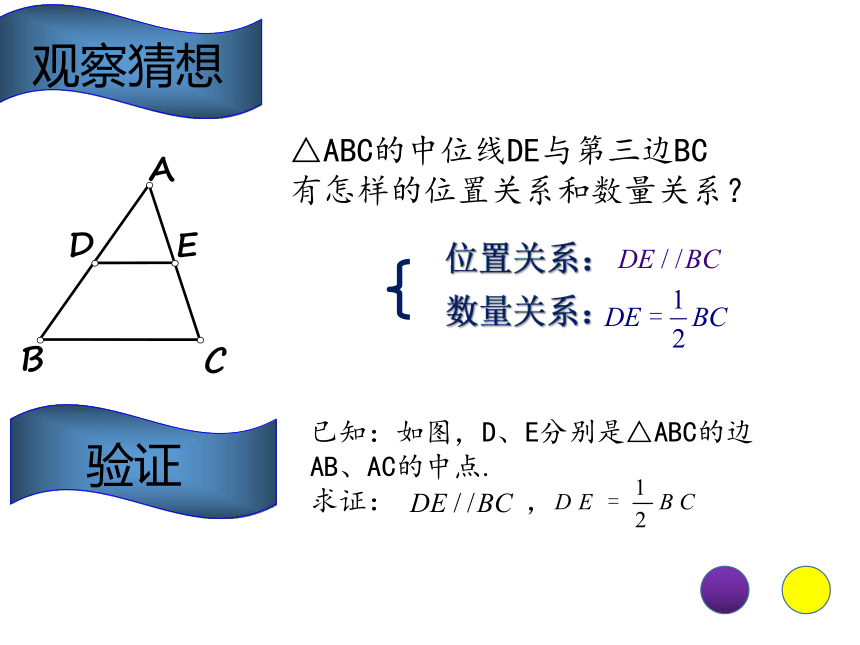
线段叫做三角形的中位线.思考:1.一个三角形有几条中位线呢? 2.中位线和中线有什么区别?像DE这样的线段称为中位线△ABC的中位线DE与第三边BC有怎样的位置关系和数量关系?已知:如图,D、E分别是△ABC的边AB、AC的中点.
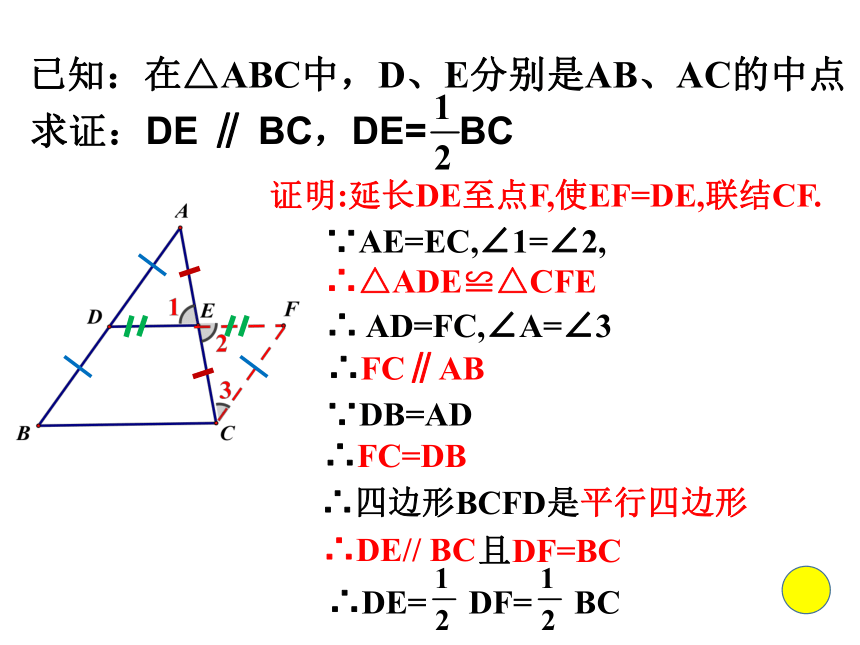
求证: ,观察猜想数量关系:位置关系: 验证已知:在△ABC中,D、E分别是AB、AC的中点求证:DE ∥ BC,DE= BC 证明:延长DE至点F,使EF=DE,联结CF.
∵AE=EC,∠1=∠2,
∴△ADE≌△CFE ∴四边形BCFD是平行四边形∴DE// BC∴DE= DF= BC且DF=BC∴FC∥AB∵DB=AD∴ AD=FC,∠A=∠3∴FC=DB
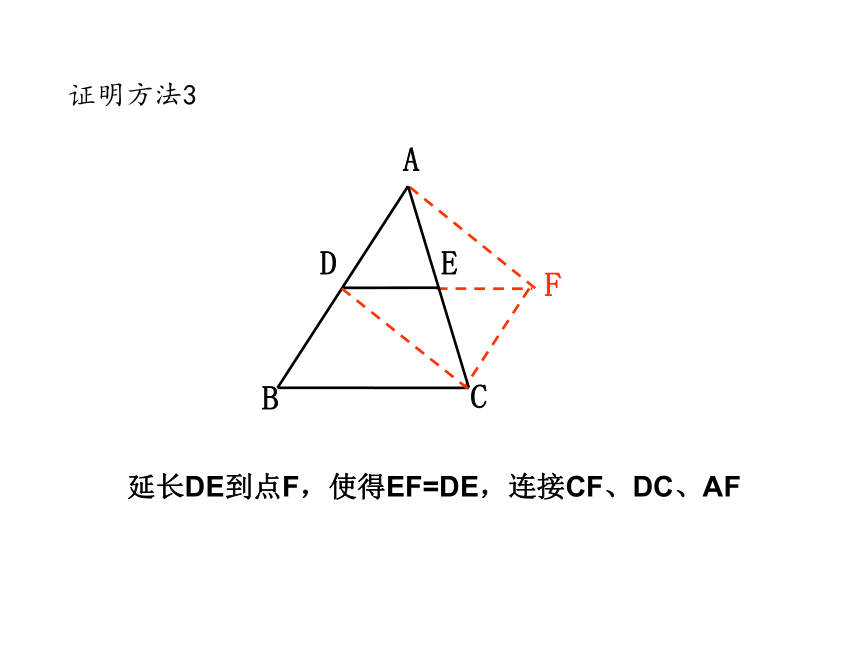
CEDAB过点C作AB的平行线,并且交DE的延长线于点FF证明方法3FBCED延长DE到点F,使得EF=DE,连接CF、DC、AFA① 证明直线平行
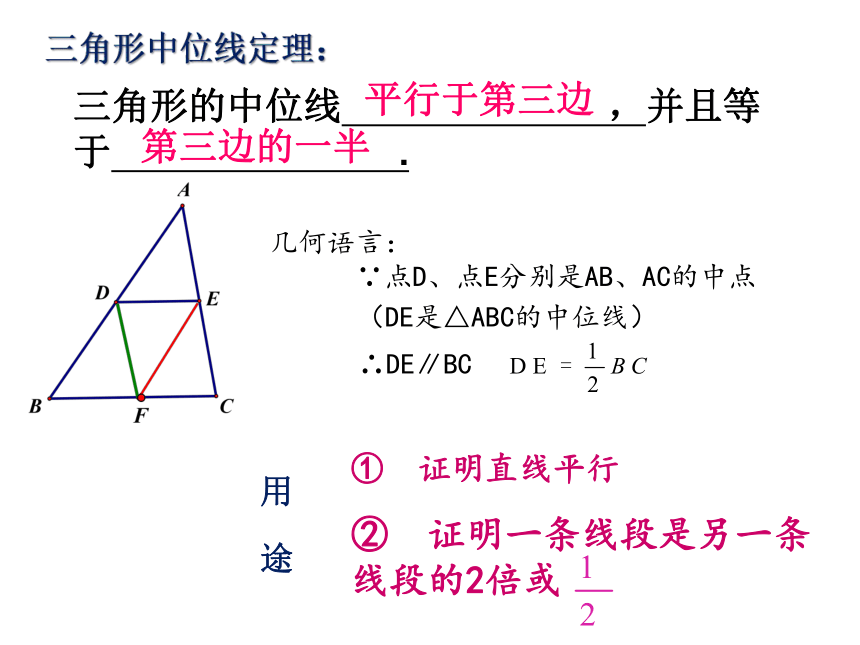
② 证明一条线段是另一条线段的2倍或用 途C三角形中位线定理:三角形的中位线 ,并且等于 .平行于第三边第三边的一半几何语言:
∵点D、点E分别是AB、AC的中点 (DE是△ABC的中位线)∴DE∥BC 1.如图,△ABC中,D、E、F
分别是AB、BC、AC的中点,①若DF=5,则BC=___;③若AB=8,则EF=___;②若∠B=50。,则∠ADF=____;10450。④若G,H分别是BD,BE的中点,求证:GH//AC.1084初显身手2、如图,漂漂想要测量B、C 两点之间的距离,但它们被池塘隔开不能直接测量。你能用今天所学的知识来帮助漂漂解决这个问题吗?.A.A2、如图,漂漂想要测量B、C 两点之间的距离,但它们被池塘隔开不能直接测量。你能用今天所学的知识来帮助漂漂解决这个问题吗?.A.AGH3. 已知:如图,在四边形ABCD中,E、F、G、H分别
是AB、BC、CD、DA的中点。
求证:四边形EFGH是平行四边形。
证明:联结BD∵E、H分别是AB、AD的中点∴EH//BD 同理FG//BD ∴四边形EFGH为平行四边形(三角形的中位线平行于第三边,并且等于第三边的一半)∴EH//FG EH=FGAC⊥BDAC=BDAC⊥BD,AC=BD变式训练矩形菱形正方形1)若AC⊥BD时矩形菱形2)若AC=BD时若AC⊥BD,AC=BD时正方形AC⊥BDAC=BDAC⊥BD,AC=BD变式训练矩形菱形正方形已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点. 则 (1)四边形EFGH是( )
(2)请增加一个条件使得四边形EFGH为菱形。(3) 请增加一个条件使得四边形EFGH为矩形。挑战自我(逆向思维)平行四边形AC=BDAC⊥BD谈谈收获同学们:
今天你收获了什么?
作业布置:
1.练习册 习题22.6(1)
2.选做题: 三角形的中位线 还有别的什么证明方法?
Thank You !在四边形ABCD中,AD=BC,E、F分别是CD、BC的中点,直线EF分别交BC、AD延长线于点G、H,求证:∠G=∠1GABCDEFH1思维拓展谈谈收获同学们:
今天你收获了什么?
辅助线的添加方法一个中点两个中点辅助线方法构造“8”字形全等中位线定理
线段叫做三角形的中位线.思考:1.一个三角形有几条中位线呢? 2.中位线和中线有什么区别?像DE这样的线段称为中位线△ABC的中位线DE与第三边BC有怎样的位置关系和数量关系?已知:如图,D、E分别是△ABC的边AB、AC的中点.
求证: ,观察猜想数量关系:位置关系: 验证已知:在△ABC中,D、E分别是AB、AC的中点求证:DE ∥ BC,DE= BC 证明:延长DE至点F,使EF=DE,联结CF.
∵AE=EC,∠1=∠2,
∴△ADE≌△CFE ∴四边形BCFD是平行四边形∴DE// BC∴DE= DF= BC且DF=BC∴FC∥AB∵DB=AD∴ AD=FC,∠A=∠3∴FC=DB
CEDAB过点C作AB的平行线,并且交DE的延长线于点FF证明方法3FBCED延长DE到点F,使得EF=DE,连接CF、DC、AFA① 证明直线平行
② 证明一条线段是另一条线段的2倍或用 途C三角形中位线定理:三角形的中位线 ,并且等于 .平行于第三边第三边的一半几何语言:
∵点D、点E分别是AB、AC的中点 (DE是△ABC的中位线)∴DE∥BC 1.如图,△ABC中,D、E、F
分别是AB、BC、AC的中点,①若DF=5,则BC=___;③若AB=8,则EF=___;②若∠B=50。,则∠ADF=____;10450。④若G,H分别是BD,BE的中点,求证:GH//AC.1084初显身手2、如图,漂漂想要测量B、C 两点之间的距离,但它们被池塘隔开不能直接测量。你能用今天所学的知识来帮助漂漂解决这个问题吗?.A.A2、如图,漂漂想要测量B、C 两点之间的距离,但它们被池塘隔开不能直接测量。你能用今天所学的知识来帮助漂漂解决这个问题吗?.A.AGH3. 已知:如图,在四边形ABCD中,E、F、G、H分别
是AB、BC、CD、DA的中点。
求证:四边形EFGH是平行四边形。
证明:联结BD∵E、H分别是AB、AD的中点∴EH//BD 同理FG//BD ∴四边形EFGH为平行四边形(三角形的中位线平行于第三边,并且等于第三边的一半)∴EH//FG EH=FGAC⊥BDAC=BDAC⊥BD,AC=BD变式训练矩形菱形正方形1)若AC⊥BD时矩形菱形2)若AC=BD时若AC⊥BD,AC=BD时正方形AC⊥BDAC=BDAC⊥BD,AC=BD变式训练矩形菱形正方形已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点. 则 (1)四边形EFGH是( )
(2)请增加一个条件使得四边形EFGH为菱形。(3) 请增加一个条件使得四边形EFGH为矩形。挑战自我(逆向思维)平行四边形AC=BDAC⊥BD谈谈收获同学们:
今天你收获了什么?
作业布置:
1.练习册 习题22.6(1)
2.选做题: 三角形的中位线 还有别的什么证明方法?
Thank You !在四边形ABCD中,AD=BC,E、F分别是CD、BC的中点,直线EF分别交BC、AD延长线于点G、H,求证:∠G=∠1GABCDEFH1思维拓展谈谈收获同学们:
今天你收获了什么?
辅助线的添加方法一个中点两个中点辅助线方法构造“8”字形全等中位线定理
