22.6(1) 三角形的中位线定理 课件(19张PPT)
文档属性
| 名称 | 22.6(1) 三角形的中位线定理 课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 284.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 09:34:08 | ||
图片预览


文档简介
课件19张PPT。(1)在同一底上的两个内角____的梯形
是等腰梯形.
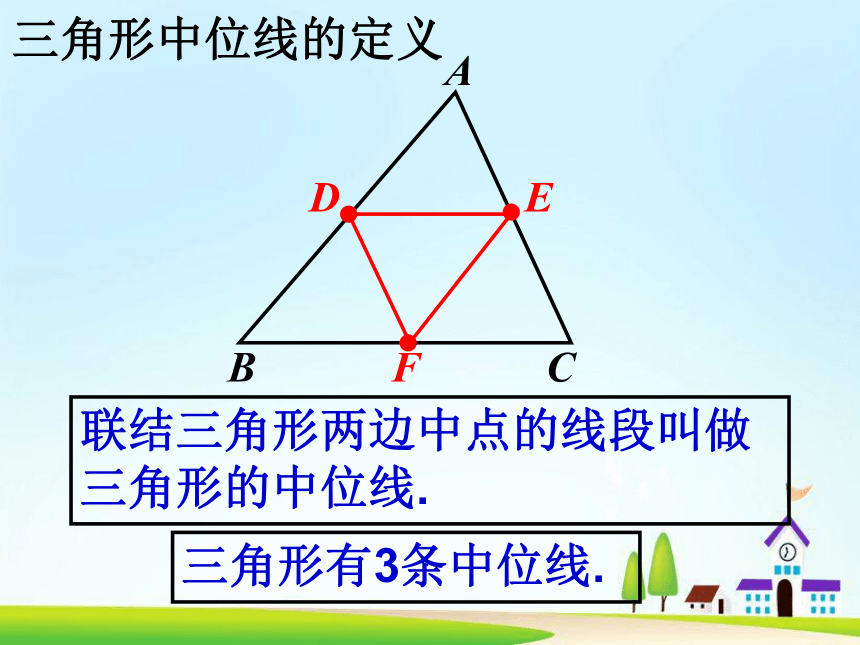
(2)对角线____的梯形是等腰梯形.相等 相等 22.6(1)三角形的中位线定理联结三角形两边中点的线段叫做
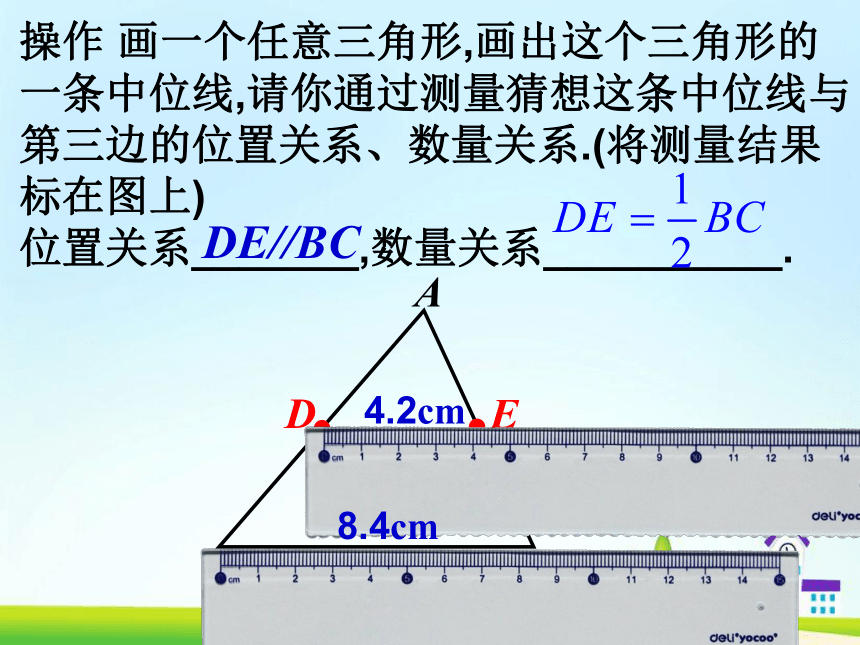
三角形的中位线.ACB三角形中位线的定义三角形有3条中位线.操作 画一个任意三角形,画出这个三角形的
一条中位线,请你通过测量猜想这条中位线与
第三边的位置关系、数量关系.(将测量结果
标在图上)
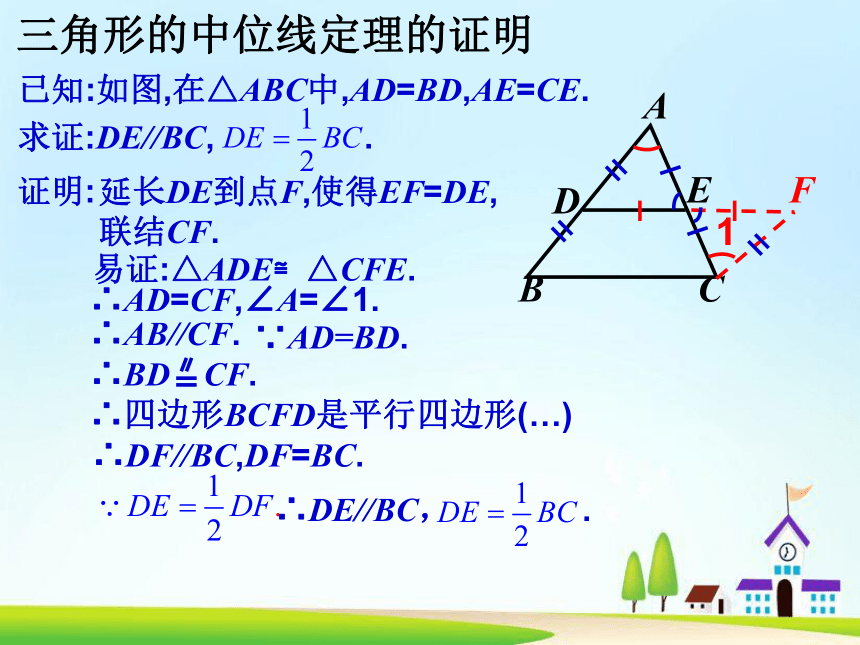
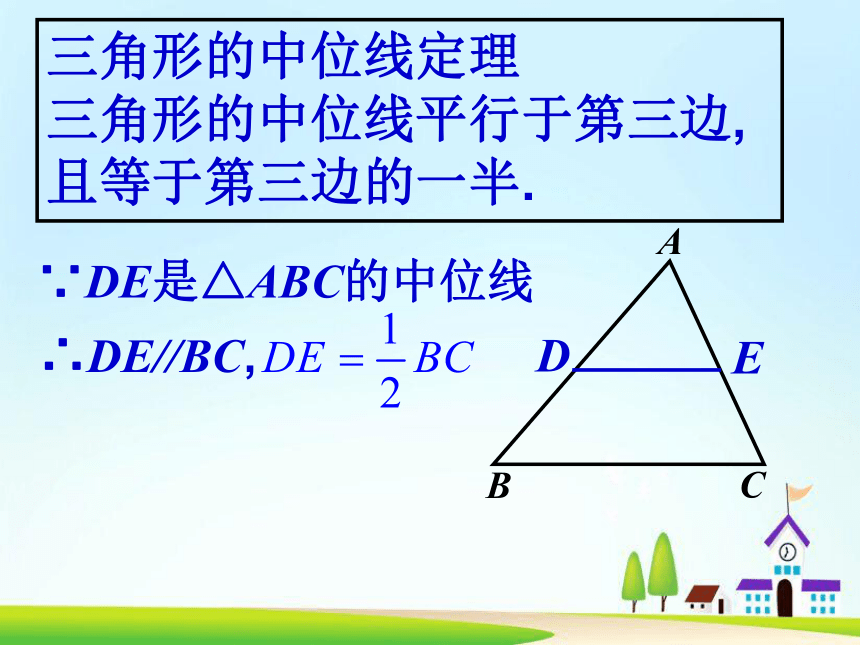
位置关系_______,数量关系__________.ACBDE//BC4.2cm8.4cmAEDCB三角形的中位线定理的证明三角形的中位线定理
三角形的中位线平行于第三边,
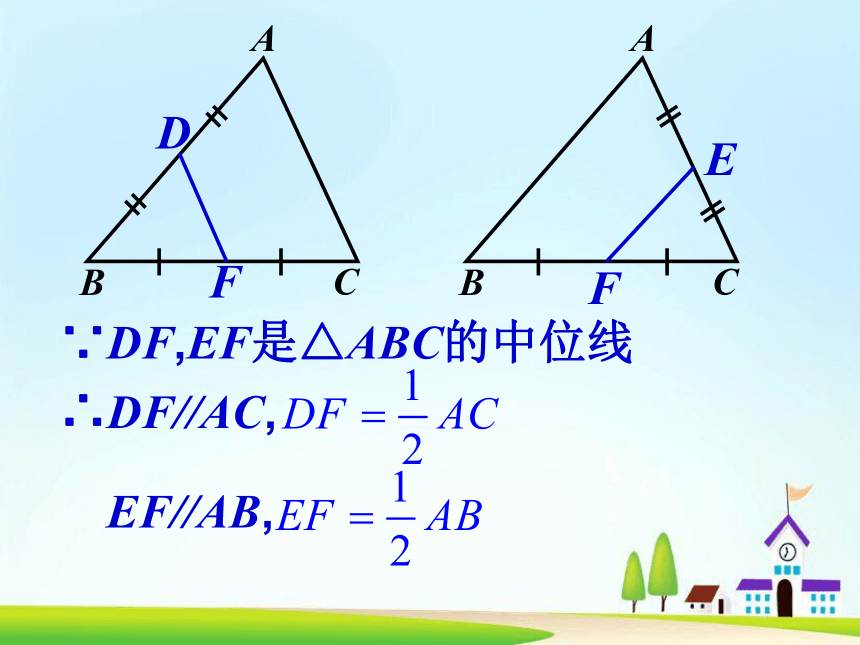
且等于第三边的一半.AEDCB∴DE//BC,∵DE是△ABC的中位线AFDCBAEFCB∴DF//AC,∵DF,EF是△ABC的中位线EF//AB,例题1 已知:如图,点O是△ABC内任意一点,D、E、F、G分别是OA、OB、BC、AC的中点.求证:四边形DEFG是平行四
边形.ADCBEOGF练习1 如图,已知在△ABC中, ∠C=900,
CD是AB边上的中线,E、F分别是BC、AC
的中点.求证:(1)CD=EF;(2)四边形CFDE是
矩形.证明:(1)∵∠C=90o,CD是AB
边上的中线∴D是AB的中点,(…)∴CD=EF∴EF//AB,(2)∵DE、DF是△ABC的中位线∵E、F分别是BC、AC的中点∴DE//CF, DF//CE∴四边形CFDE是
平行四边形.∵∠C=90o∴四边形CFDE是
矩形(…)练习2 如图,已知AD=DB,AE=EC.如果BC= ,那么DE=____;
如果DE=5,那么BC=____.105练习3 已知:如图,△ABC中,D、E、F
分别是AB、BC、CA三边的中点.
求证:中位线DF和中线AE互相平分.ACBDFE证明:联结DE、EF
∵D、E、F分别是AB、BC、CA
三边的中点
∴DE、EF是△ABC的中位线
∴DE//AC,EF//AB
∴四边形EFAD是平行四边形
(平行四边形的定义)
∴DF与AE互相平分
(平行四边形的对角线互相平分)练习4 如图,B、C两点被海水隔开,在B、
C外选择一点A,找到AB、AC的中点E、F,
测量得EF=22米,求出B、C两点的距离.ACBEF22海水解:∵E、F分别是AB
、AC的中点
∴EF是△ABC的中位线
∴BC=2EF(三角形的中
位线等于第三边的一半)
∵EF=22(米)
∴BC=44(米)
答:B、C两点的距离为44米.练习5 求证: 顺次联结四边形四条边的中点,
所得的四边形是平行四边形.∴EF//GH,EF=GH,EH//FG,EH=FG
∴四边形EFGH是平行四边形(平行四边形的定义)ABCFHEG对角线AC⊥BDD探究 定义 顺次联结四边形各边中点得到的四边形,
叫做原四边形的中点四边形.
例如:任意四边形的中点四边形都是平行四边形.
如图,四边形EFGH为四边形ABCD的中点四边形.矩形菱形正方形总结规律:
(1)对角线互相垂直的四边形的中点四边形是____.
(2)对角线相等的四边形的中点四边形是____.
(3)对角线互相垂直且相等的四边形的中点四边形
是______.正方形菱形矩形ABCDFHEG正方形ABCDABCDFHEGABCDFHEG等腰梯形ABCD□ABCDABCDFHEG任意四边形ABCDABCDFHEG矩形ABCDABCDFHEG菱形ABCD平行四边形菱形矩形正方形菱形平行四边形请同学们谈谈本堂课都学习了什么内容?三角形的中位线的定义遇中点,连出中位线或三角形.拓展 已知:如图,在△ABC中,AG⊥BC于点G,
点E、F、H分别为AB、BC、CA的中点.
求证:四边形EFGH为等腰梯形.证明:∵EF、EH是△ABC的中位线∴EF//AC,∵AG⊥BC,GH是△ABC
的中线EH//BC,∴EF=GH∵∠1=∠2,∠3=∠4
∠2=∠C证明:∵EF、EH是△ABC的中位线∴DE//AC,∵AG⊥BC,GH是△ABC
的中线EH//BC,∴EH=GH∵∠1=∠2,∠3=∠4
∠2=∠C∴∠1+∠3=∠2+∠4=∠C+∠4<180o∴EF与GH不平行∴四边形EFGH为梯形.∵EF=GH∴四边形EFGH为等腰梯形.
是等腰梯形.
(2)对角线____的梯形是等腰梯形.相等 相等 22.6(1)三角形的中位线定理联结三角形两边中点的线段叫做
三角形的中位线.ACB三角形中位线的定义三角形有3条中位线.操作 画一个任意三角形,画出这个三角形的
一条中位线,请你通过测量猜想这条中位线与
第三边的位置关系、数量关系.(将测量结果
标在图上)
位置关系_______,数量关系__________.ACBDE//BC4.2cm8.4cmAEDCB三角形的中位线定理的证明三角形的中位线定理
三角形的中位线平行于第三边,
且等于第三边的一半.AEDCB∴DE//BC,∵DE是△ABC的中位线AFDCBAEFCB∴DF//AC,∵DF,EF是△ABC的中位线EF//AB,例题1 已知:如图,点O是△ABC内任意一点,D、E、F、G分别是OA、OB、BC、AC的中点.求证:四边形DEFG是平行四
边形.ADCBEOGF练习1 如图,已知在△ABC中, ∠C=900,
CD是AB边上的中线,E、F分别是BC、AC
的中点.求证:(1)CD=EF;(2)四边形CFDE是
矩形.证明:(1)∵∠C=90o,CD是AB
边上的中线∴D是AB的中点,(…)∴CD=EF∴EF//AB,(2)∵DE、DF是△ABC的中位线∵E、F分别是BC、AC的中点∴DE//CF, DF//CE∴四边形CFDE是
平行四边形.∵∠C=90o∴四边形CFDE是
矩形(…)练习2 如图,已知AD=DB,AE=EC.如果BC= ,那么DE=____;
如果DE=5,那么BC=____.105练习3 已知:如图,△ABC中,D、E、F
分别是AB、BC、CA三边的中点.
求证:中位线DF和中线AE互相平分.ACBDFE证明:联结DE、EF
∵D、E、F分别是AB、BC、CA
三边的中点
∴DE、EF是△ABC的中位线
∴DE//AC,EF//AB
∴四边形EFAD是平行四边形
(平行四边形的定义)
∴DF与AE互相平分
(平行四边形的对角线互相平分)练习4 如图,B、C两点被海水隔开,在B、
C外选择一点A,找到AB、AC的中点E、F,
测量得EF=22米,求出B、C两点的距离.ACBEF22海水解:∵E、F分别是AB
、AC的中点
∴EF是△ABC的中位线
∴BC=2EF(三角形的中
位线等于第三边的一半)
∵EF=22(米)
∴BC=44(米)
答:B、C两点的距离为44米.练习5 求证: 顺次联结四边形四条边的中点,
所得的四边形是平行四边形.∴EF//GH,EF=GH,EH//FG,EH=FG
∴四边形EFGH是平行四边形(平行四边形的定义)ABCFHEG对角线AC⊥BDD探究 定义 顺次联结四边形各边中点得到的四边形,
叫做原四边形的中点四边形.
例如:任意四边形的中点四边形都是平行四边形.
如图,四边形EFGH为四边形ABCD的中点四边形.矩形菱形正方形总结规律:
(1)对角线互相垂直的四边形的中点四边形是____.
(2)对角线相等的四边形的中点四边形是____.
(3)对角线互相垂直且相等的四边形的中点四边形
是______.正方形菱形矩形ABCDFHEG正方形ABCDABCDFHEGABCDFHEG等腰梯形ABCD□ABCDABCDFHEG任意四边形ABCDABCDFHEG矩形ABCDABCDFHEG菱形ABCD平行四边形菱形矩形正方形菱形平行四边形请同学们谈谈本堂课都学习了什么内容?三角形的中位线的定义遇中点,连出中位线或三角形.拓展 已知:如图,在△ABC中,AG⊥BC于点G,
点E、F、H分别为AB、BC、CA的中点.
求证:四边形EFGH为等腰梯形.证明:∵EF、EH是△ABC的中位线∴EF//AC,∵AG⊥BC,GH是△ABC
的中线EH//BC,∴EF=GH∵∠1=∠2,∠3=∠4
∠2=∠C证明:∵EF、EH是△ABC的中位线∴DE//AC,∵AG⊥BC,GH是△ABC
的中线EH//BC,∴EH=GH∵∠1=∠2,∠3=∠4
∠2=∠C∴∠1+∠3=∠2+∠4=∠C+∠4<180o∴EF与GH不平行∴四边形EFGH为梯形.∵EF=GH∴四边形EFGH为等腰梯形.
