22.6 三角形、梯形的中位线(1) 课件(16张PPT)
文档属性
| 名称 | 22.6 三角形、梯形的中位线(1) 课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 687.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 00:00:00 | ||
图片预览


文档简介
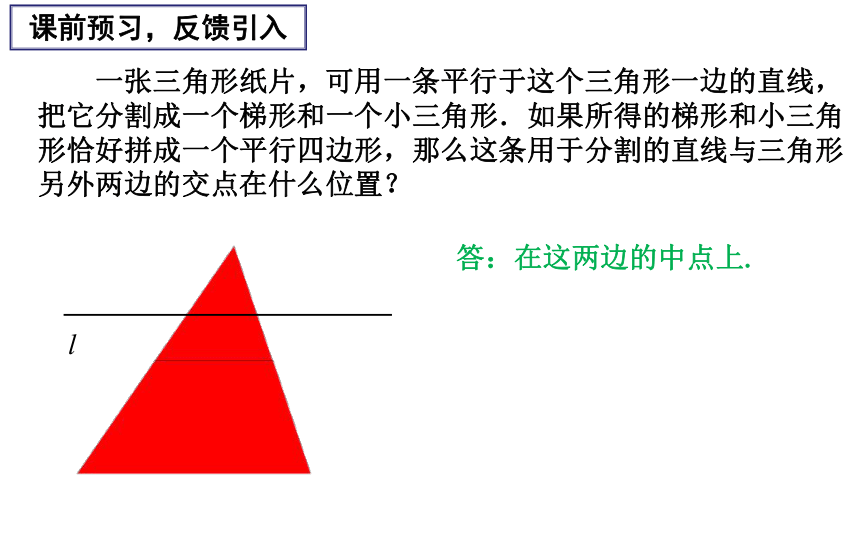
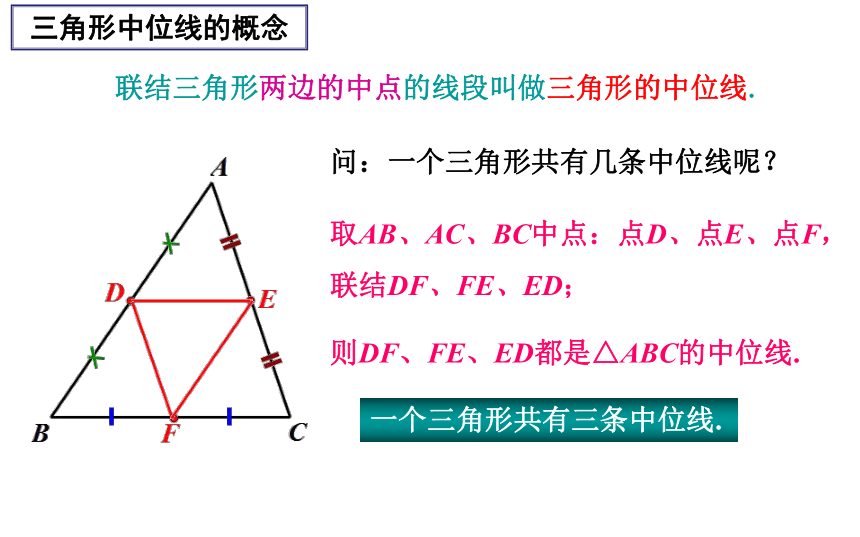
课件16张PPT。§22.6 三角形的中位线(1)课前预习,反馈引入 一张三角形纸片,可用一条平行于这个三角形一边的直线,把它分割成一个梯形和一个小三角形.如果所得的梯形和小三角形恰好拼成一个平行四边形,那么这条用于分割的直线与三角形另外两边的交点在什么位置?l答:在这两边的中点上.问:一个三角形共有几条中位线呢? 取AB、AC、BC中点:点D、点E、点F,
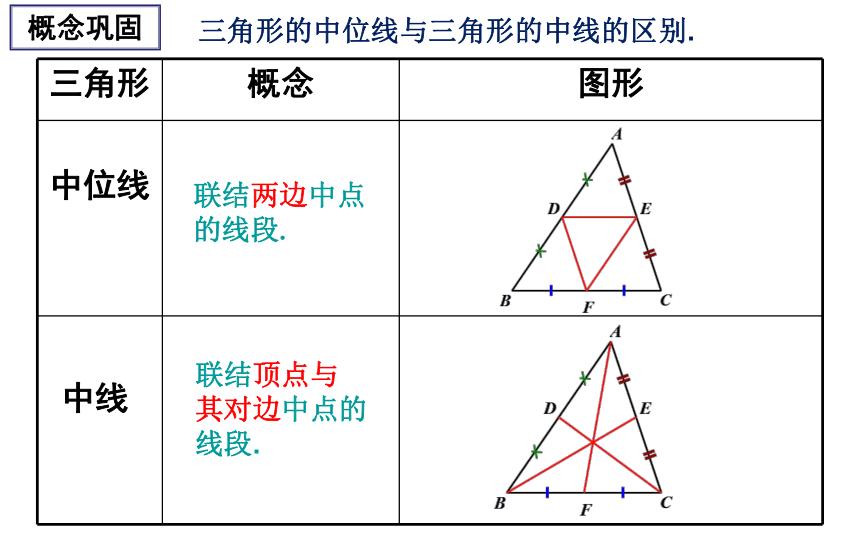
联结DF、FE、ED; 则DF、FE、ED都是△ABC的中位线. 一个三角形共有三条中位线. 联结三角形两边的中点的线段叫做三角形的中位线.三角形中位线的概念三角形的中位线与三角形的中线的区别. 联结两边中点的线段. 联结顶点与
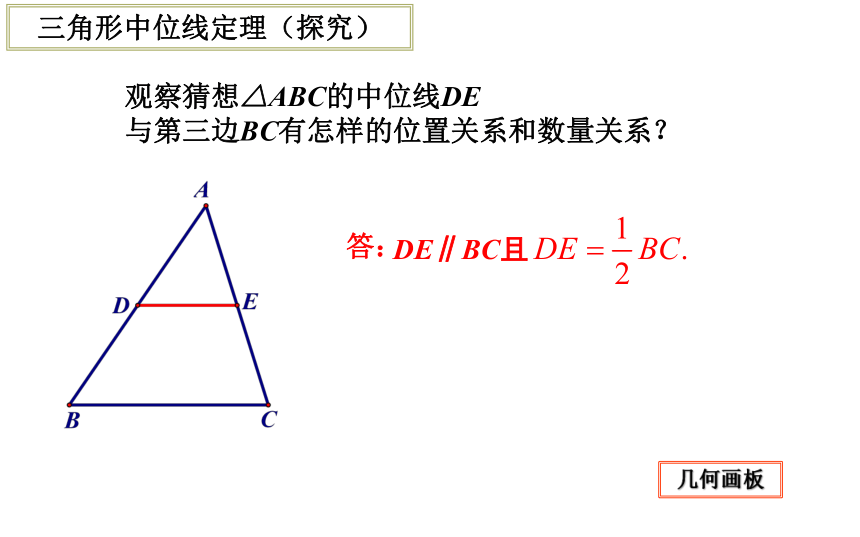
其对边中点的线段. 中线概念巩固 观察猜想△ABC的中位线DE
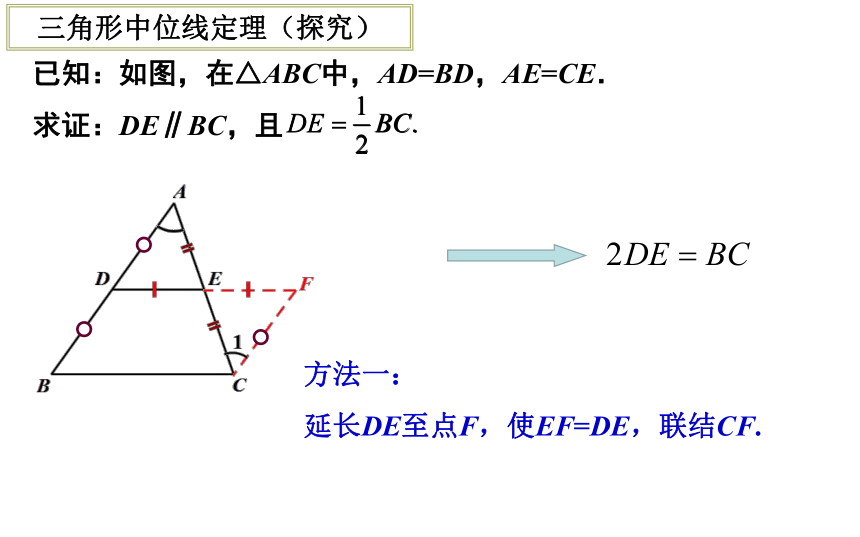
与第三边BC有怎样的位置关系和数量关系? 三角形中位线定理(探究) 几何画板方法一:
延长DE至点F,使EF=DE,联结CF.三角形中位线定理(探究) 延长DE至点F,使EF=DE,
联结CF、AF、DC.方法二:已知:如图,在△ABC中,AD=BD,AE=CE.
求证:DE∥BC,且三角形中位线定理(探究) 取BC中点,联结GE并延长,
过点A作AF ∥BC 且相交于点F.方法三:GF已知:如图,在△ABC中,AD=BD,AE=CE.
求证:DE∥BC,且三角形中位线定理(探究) 三角形平行四边形在△ABC中,
∵ AD=BD,AE=CE,
∴ DE∥BC,且(三角形的中位线平行于第三边,并且等于第三边的一半). 符号语言:三角形的中位线平行于第三边,并且等于第三边的一半. 三角形中位线定理口答:
如图,在△ABC中,已知AD=DB,AE=EC,BF=CF.
(1)如果 ,那么DE=____;
(2)若AB=6,BC=5,CA=4,
则△ DEF的周长为________ .新知运用 7.5 例题6 已知:如图,点O是△ABC内任意一点,D、E、F、G分别是OB、 OC、AC、AB的中点.
求证:四边形DEFG是平行四边形.由已知条件你能在图中找到什么? 新知运用 四边形DEFG是平行四边形.例题6 已知:如图,点O是△ABC内任意一点,D、E、F、G分别是OB、 OC、AC、AB的中点.
求证:四边形DEFG是平行四边形.证明:∵ 点G、F分别为AB、AC的中点,∴GF∥DE,且GF=DE.∴四边形DEFG是平行四边形
(一组对边平行且相等的四边形是平行四边形).例题讲解 例题6 已知:如图,点O是△ABC内任意一点,D、E、F、G分别是OB、 OC、AC、AB的中点.
求证:四边形DEFG是平行四边形.变式:如图,点O是△ABC外一点,以上结论是否还成立?答:结论成立. 变点O的位置不变GF、DE仍是△ABC和△OBC的中位线,且这两个三角形有公共边BC.结论四边形DEFG是平行四边形.例题讲解 几何画板通过本课的学习你有何收获? 1、三角形中位线的概念 2、三角形中位线定理 联结三角形两边的中点的线段叫做三角形的中位线. 课堂小结 3、数学思想形变质不变作业:
1.完成书p98/2、3;
2.完成学习单. 例题6 已知:如图,点O是△ABC内任意一点,D、E、F、G分别是OB、 OC、AC、AB的中点.
求证:四边形DEFG是平行四边形.现在你还能找到其他中位线吗? 新知运用
联结DF、FE、ED; 则DF、FE、ED都是△ABC的中位线. 一个三角形共有三条中位线. 联结三角形两边的中点的线段叫做三角形的中位线.三角形中位线的概念三角形的中位线与三角形的中线的区别. 联结两边中点的线段. 联结顶点与
其对边中点的线段. 中线概念巩固 观察猜想△ABC的中位线DE
与第三边BC有怎样的位置关系和数量关系? 三角形中位线定理(探究) 几何画板方法一:
延长DE至点F,使EF=DE,联结CF.三角形中位线定理(探究) 延长DE至点F,使EF=DE,
联结CF、AF、DC.方法二:已知:如图,在△ABC中,AD=BD,AE=CE.
求证:DE∥BC,且三角形中位线定理(探究) 取BC中点,联结GE并延长,
过点A作AF ∥BC 且相交于点F.方法三:GF已知:如图,在△ABC中,AD=BD,AE=CE.
求证:DE∥BC,且三角形中位线定理(探究) 三角形平行四边形在△ABC中,
∵ AD=BD,AE=CE,
∴ DE∥BC,且(三角形的中位线平行于第三边,并且等于第三边的一半). 符号语言:三角形的中位线平行于第三边,并且等于第三边的一半. 三角形中位线定理口答:
如图,在△ABC中,已知AD=DB,AE=EC,BF=CF.
(1)如果 ,那么DE=____;
(2)若AB=6,BC=5,CA=4,
则△ DEF的周长为________ .新知运用 7.5 例题6 已知:如图,点O是△ABC内任意一点,D、E、F、G分别是OB、 OC、AC、AB的中点.
求证:四边形DEFG是平行四边形.由已知条件你能在图中找到什么? 新知运用 四边形DEFG是平行四边形.例题6 已知:如图,点O是△ABC内任意一点,D、E、F、G分别是OB、 OC、AC、AB的中点.
求证:四边形DEFG是平行四边形.证明:∵ 点G、F分别为AB、AC的中点,∴GF∥DE,且GF=DE.∴四边形DEFG是平行四边形
(一组对边平行且相等的四边形是平行四边形).例题讲解 例题6 已知:如图,点O是△ABC内任意一点,D、E、F、G分别是OB、 OC、AC、AB的中点.
求证:四边形DEFG是平行四边形.变式:如图,点O是△ABC外一点,以上结论是否还成立?答:结论成立. 变点O的位置不变GF、DE仍是△ABC和△OBC的中位线,且这两个三角形有公共边BC.结论四边形DEFG是平行四边形.例题讲解 几何画板通过本课的学习你有何收获? 1、三角形中位线的概念 2、三角形中位线定理 联结三角形两边的中点的线段叫做三角形的中位线. 课堂小结 3、数学思想形变质不变作业:
1.完成书p98/2、3;
2.完成学习单. 例题6 已知:如图,点O是△ABC内任意一点,D、E、F、G分别是OB、 OC、AC、AB的中点.
求证:四边形DEFG是平行四边形.现在你还能找到其他中位线吗? 新知运用
