22.6 三角形、梯形的中位线(2) 课件(17张PPT)
文档属性
| 名称 | 22.6 三角形、梯形的中位线(2) 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 586.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 09:37:42 | ||
图片预览


文档简介
课件17张PPT。§22.6 三角形、梯形的中位线(2) 复习引入1、什么叫三角形的中位线?三角形的中位线是三角形中的特殊线段,那么在四边形中有这样特殊的线段吗?这节课我们将进行探究. ∵DE是△ ABC的中位线(已知)2、三角形的中位线有什么性质?答:联结三角形两边中点的线段叫做三角形的中位线. 答:三角形的中位线平行于第三边,并且等于第三边的一半.符号语言: (三角形的中位线平行于第三边,
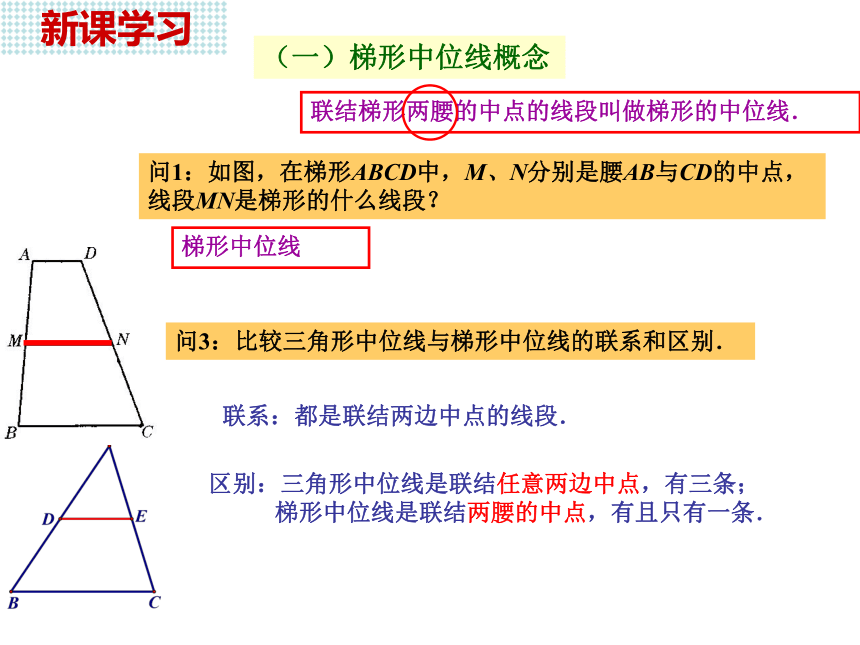
并且等于第三边的一半.)问1:如图,在梯形ABCD中,M、N分别是腰AB与CD的中点,线段MN是梯形的什么线段? 新课学习(一)梯形中位线概念区别:三角形中位线是联结任意两边中点,有三条;
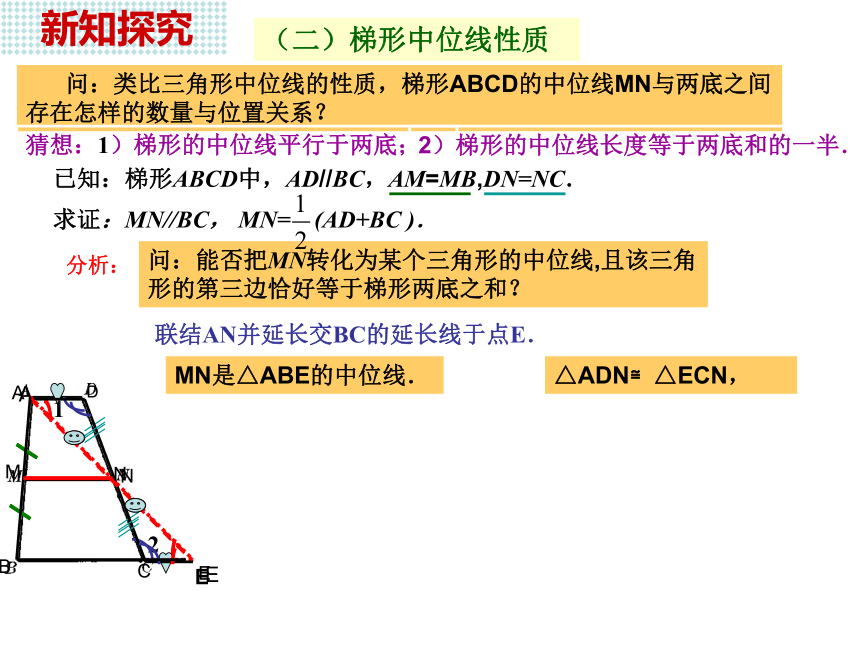
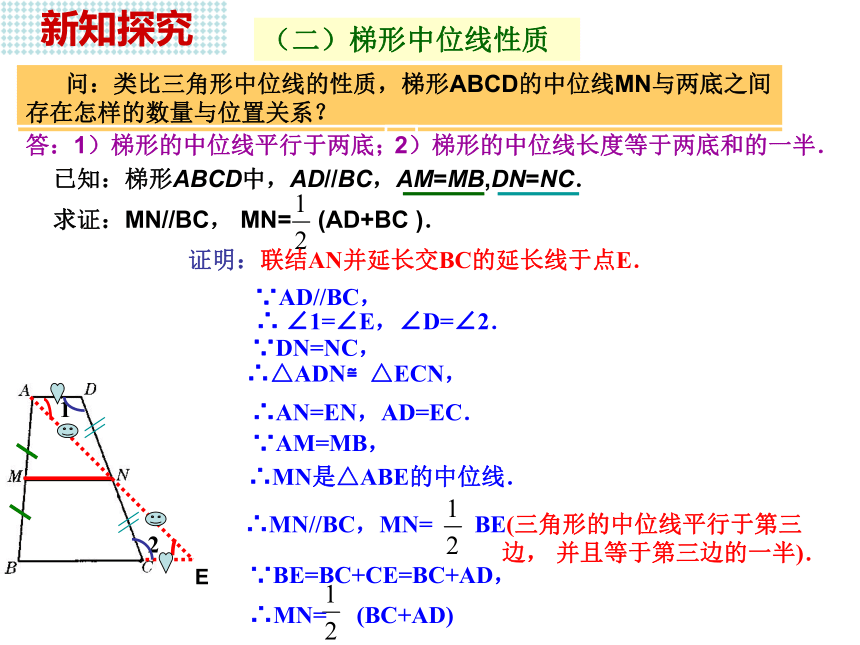
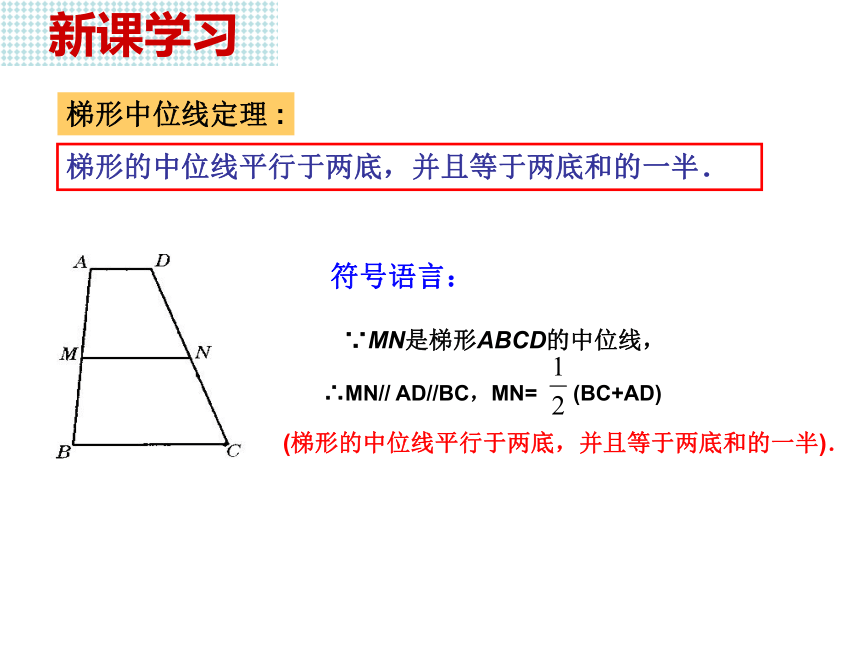
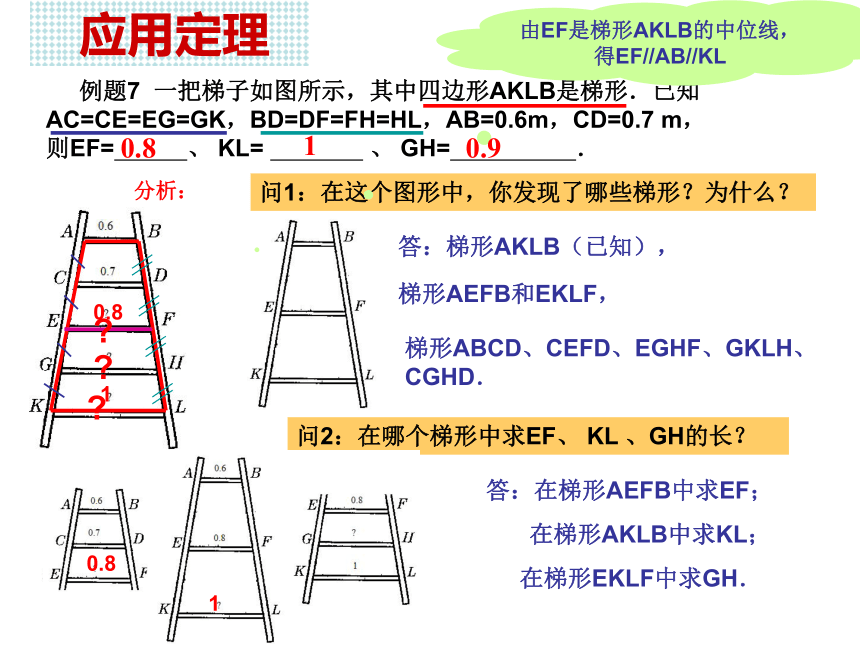
梯形中位线是联结两腰的中点,有且只有一条. 问3:比较三角形中位线与梯形中位线的联系和区别.联系:都是联结两边中点的线段.梯形中位线联结梯形两腰的中点的线段叫做梯形的中位线. 新知探究(二)梯形中位线性质 问:类比三角形中位线的性质,梯形ABCD的中位线MN与两底之间存在怎样的数量与位置关系?已知:梯形ABCD中,AD//BC,AM=MB,DN=NC.问:能否把MN转化为某个三角形的中位线,且该三角形的第三边恰好等于梯形两底之和?猜想:1)梯形的中位线平行于两底;2)梯形的中位线长度等于两底和的一半.E21联结AN并延长交BC的延长线于点E.分析:△ADN≌△ECN, MN是△ABE的中位线.(二)梯形中位线性质 问:类比三角形中位线的性质,梯形ABCD的中位线MN与两底之间存在怎样的数量与位置关系?已知:梯形ABCD中,AD//BC,AM=MB,DN=NC.答:1)梯形的中位线平行于两底;2)梯形的中位线长度等于两底和的一半.E21证明:联结AN并延长交BC的延长线于点E.∵AD//BC,∴ ∠1=∠E,∠D=∠2.∵DN=NC,∴△ADN≌△ECN, ∴AN=EN,AD=EC.∵AM=MB, ∴MN是△ABE的中位线.∵BE=BC+CE=BC+AD, 新知探究 新课学习梯形的中位线平行于两底,并且等于两底和的一半. 符号语言:∵MN是梯形ABCD的中位线, (梯形的中位线平行于两底,并且等于两底和的一半).梯形中位线定理 : 应用定理 例题7 一把梯子如图所示,其中四边形AKLB是梯形.已知AC=CE=EG=GK,BD=DF=FH=HL,AB=0.6m,CD=0.7 m,
则EF= 、 KL= 、 GH= .问1:在这个图形中,你发现了哪些梯形?为什么?问2:在哪个梯形中求EF、 KL 、GH的长?分析:梯形ABCD、CEFD、EGHF、GKLH、CGHD.在梯形EKLF中求GH.梯形AEFB和EKLF,答:梯形AKLB(已知),答:在梯形AEFB中求EF;在梯形AKLB中求KL;由EF是梯形AKLB的中位线,得EF//AB//KL0.80.811???0.810.9 应用定理例题8 已知:梯形ABCD中,AD//BC,E为AB中点,AD+BC=DC.
求证:DE⊥EC,DE平分∠ADC,CE平分∠BCD.问1:已知条件中有AD+BC,那么如何把它们加在一起?延长DE交CB的延长线于点F.F可证△ADE≌△BFE, ????分析: 应用定理例题8 已知:梯形ABCD中,AD//BC,E为AB中点AD+BC=DC.
求证:DE⊥EC,DE平分∠ADC,CE平分∠BCD.问2:学习了梯形中位线定理后,还有其他方法吗?答:添梯形的中位线. F取DC中点F,联结EF.123456分析: 应用定理例题8 已知:梯形ABCD中,AD//BC,E为AB中点,AD+BC=DC.
求证:DE⊥EC,DE平分∠ADC,CE平分∠BCD.【适时小结】
梯形添加辅助线的方法:
添梯形的中位线.F123456证明:取DC中点F,联结EF.∵E为AB中点,∴EF为梯形的中位线,(梯形的中位线平行于两底,并且等于两底和的一半).∴∠l=∠5.∵DC=AD+BC,∴EF=DC=DF.∴∠1=∠2.∴∠2=∠5,即DE平分∠ADC.同理,CE平分∠BCD.∴DE⊥CE. 课堂练习课本P100 第1题(口答)1.如图,梯形ABCD中,AD//BC,MN是它的中位线,
(1)如果AD=3,BC=5,那么MN= ;
(2)如果AD=5,MN=7,那么BC= ;
(3)如果BC=a,MN=3,那么AD= .“知二求一”:在梯形的上底、下底、中位线的三条线段中,已知其中两条线段的长度,就可求第三条线段的长度.4;9;6?a.【适时小结】课本P100 第2、3题2.已知梯形的中位线长为m米,高为h米,那么梯形的面积是多少平方米? 课堂练习3.如图是一个形如直角梯形的鱼塘,已知AB=200m,BC=400m,CD=250m,E、F分别是AD、BC的中点.现要在E、F处建一道隔离栏,把鱼塘分给两家渔民进行承包,并且约定承包费用按照水面面积分摊,那么应按什么比例来分摊总承包金额?BF=FC∴EF为梯形ABCD的中位线,解∵ E、F分别是AD、BC的中点,2. 梯形中位线定理:梯形的中位线平行于两底,并且等于两底和的一半. 课堂小结符号语言:∵MN是梯形ABCD的中位线, (梯形的中位线平行于两底,并且等于两底和的一半).通过这节课的学习,你有什么收获和体会?1.梯形中位线的概念:联结梯形两腰的中点的线段叫做梯形的中位线. 3. 梯形添加辅助线的方法: 课堂小结(2)添梯形的中位线. 4.类比、化归、图形的分解组合的数学思想.(1)关于腰中点构造中心对称的全等三角形; 布置作业《练习册》 习题22.6(2) 应用定理例题8 已知:梯形ABCD中,AD//BC,E为AB中点,AD+BC=DC.
求证:DE⊥EC,DE平分∠ADC,CE平分∠BCD.问1:已知条件中有AD+BC,那么如何把它们加在一起?延长DE交CB的延长线于点F.F可证△ADE≌△BFE, ????分析: 应用定理例题8 已知:梯形ABCD中,AD//BC,E为AB中点AD+BC=DC.
求证:DE⊥EC,DE平分∠ADC,CE平分∠BCD.问2:学习了梯形中位线定理后,还有其他方法吗?答:添梯形的中位线. F取DC中点F,联结EF.123456分析:
并且等于第三边的一半.)问1:如图,在梯形ABCD中,M、N分别是腰AB与CD的中点,线段MN是梯形的什么线段? 新课学习(一)梯形中位线概念区别:三角形中位线是联结任意两边中点,有三条;
梯形中位线是联结两腰的中点,有且只有一条. 问3:比较三角形中位线与梯形中位线的联系和区别.联系:都是联结两边中点的线段.梯形中位线联结梯形两腰的中点的线段叫做梯形的中位线. 新知探究(二)梯形中位线性质 问:类比三角形中位线的性质,梯形ABCD的中位线MN与两底之间存在怎样的数量与位置关系?已知:梯形ABCD中,AD//BC,AM=MB,DN=NC.问:能否把MN转化为某个三角形的中位线,且该三角形的第三边恰好等于梯形两底之和?猜想:1)梯形的中位线平行于两底;2)梯形的中位线长度等于两底和的一半.E21联结AN并延长交BC的延长线于点E.分析:△ADN≌△ECN, MN是△ABE的中位线.(二)梯形中位线性质 问:类比三角形中位线的性质,梯形ABCD的中位线MN与两底之间存在怎样的数量与位置关系?已知:梯形ABCD中,AD//BC,AM=MB,DN=NC.答:1)梯形的中位线平行于两底;2)梯形的中位线长度等于两底和的一半.E21证明:联结AN并延长交BC的延长线于点E.∵AD//BC,∴ ∠1=∠E,∠D=∠2.∵DN=NC,∴△ADN≌△ECN, ∴AN=EN,AD=EC.∵AM=MB, ∴MN是△ABE的中位线.∵BE=BC+CE=BC+AD, 新知探究 新课学习梯形的中位线平行于两底,并且等于两底和的一半. 符号语言:∵MN是梯形ABCD的中位线, (梯形的中位线平行于两底,并且等于两底和的一半).梯形中位线定理 : 应用定理 例题7 一把梯子如图所示,其中四边形AKLB是梯形.已知AC=CE=EG=GK,BD=DF=FH=HL,AB=0.6m,CD=0.7 m,
则EF= 、 KL= 、 GH= .问1:在这个图形中,你发现了哪些梯形?为什么?问2:在哪个梯形中求EF、 KL 、GH的长?分析:梯形ABCD、CEFD、EGHF、GKLH、CGHD.在梯形EKLF中求GH.梯形AEFB和EKLF,答:梯形AKLB(已知),答:在梯形AEFB中求EF;在梯形AKLB中求KL;由EF是梯形AKLB的中位线,得EF//AB//KL0.80.811???0.810.9 应用定理例题8 已知:梯形ABCD中,AD//BC,E为AB中点,AD+BC=DC.
求证:DE⊥EC,DE平分∠ADC,CE平分∠BCD.问1:已知条件中有AD+BC,那么如何把它们加在一起?延长DE交CB的延长线于点F.F可证△ADE≌△BFE, ????分析: 应用定理例题8 已知:梯形ABCD中,AD//BC,E为AB中点AD+BC=DC.
求证:DE⊥EC,DE平分∠ADC,CE平分∠BCD.问2:学习了梯形中位线定理后,还有其他方法吗?答:添梯形的中位线. F取DC中点F,联结EF.123456分析: 应用定理例题8 已知:梯形ABCD中,AD//BC,E为AB中点,AD+BC=DC.
求证:DE⊥EC,DE平分∠ADC,CE平分∠BCD.【适时小结】
梯形添加辅助线的方法:
添梯形的中位线.F123456证明:取DC中点F,联结EF.∵E为AB中点,∴EF为梯形的中位线,(梯形的中位线平行于两底,并且等于两底和的一半).∴∠l=∠5.∵DC=AD+BC,∴EF=DC=DF.∴∠1=∠2.∴∠2=∠5,即DE平分∠ADC.同理,CE平分∠BCD.∴DE⊥CE. 课堂练习课本P100 第1题(口答)1.如图,梯形ABCD中,AD//BC,MN是它的中位线,
(1)如果AD=3,BC=5,那么MN= ;
(2)如果AD=5,MN=7,那么BC= ;
(3)如果BC=a,MN=3,那么AD= .“知二求一”:在梯形的上底、下底、中位线的三条线段中,已知其中两条线段的长度,就可求第三条线段的长度.4;9;6?a.【适时小结】课本P100 第2、3题2.已知梯形的中位线长为m米,高为h米,那么梯形的面积是多少平方米? 课堂练习3.如图是一个形如直角梯形的鱼塘,已知AB=200m,BC=400m,CD=250m,E、F分别是AD、BC的中点.现要在E、F处建一道隔离栏,把鱼塘分给两家渔民进行承包,并且约定承包费用按照水面面积分摊,那么应按什么比例来分摊总承包金额?BF=FC∴EF为梯形ABCD的中位线,解∵ E、F分别是AD、BC的中点,2. 梯形中位线定理:梯形的中位线平行于两底,并且等于两底和的一半. 课堂小结符号语言:∵MN是梯形ABCD的中位线, (梯形的中位线平行于两底,并且等于两底和的一半).通过这节课的学习,你有什么收获和体会?1.梯形中位线的概念:联结梯形两腰的中点的线段叫做梯形的中位线. 3. 梯形添加辅助线的方法: 课堂小结(2)添梯形的中位线. 4.类比、化归、图形的分解组合的数学思想.(1)关于腰中点构造中心对称的全等三角形; 布置作业《练习册》 习题22.6(2) 应用定理例题8 已知:梯形ABCD中,AD//BC,E为AB中点,AD+BC=DC.
求证:DE⊥EC,DE平分∠ADC,CE平分∠BCD.问1:已知条件中有AD+BC,那么如何把它们加在一起?延长DE交CB的延长线于点F.F可证△ADE≌△BFE, ????分析: 应用定理例题8 已知:梯形ABCD中,AD//BC,E为AB中点AD+BC=DC.
求证:DE⊥EC,DE平分∠ADC,CE平分∠BCD.问2:学习了梯形中位线定理后,还有其他方法吗?答:添梯形的中位线. F取DC中点F,联结EF.123456分析:
