22.6(1) 三角形的中位线 课件(20张)
文档属性
| 名称 | 22.6(1) 三角形的中位线 课件(20张) |  | |
| 格式 | zip | ||
| 文件大小 | 963.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 09:40:06 | ||
图片预览


文档简介
课件20张PPT。三角形的中位线CBADE 若A、B两点被一池塘隔开,想要测出AB的
距离,只要在池塘外取一点C,连接CA、CB,
取CA的中点E,CB的中点D,测出ED的距离乘以
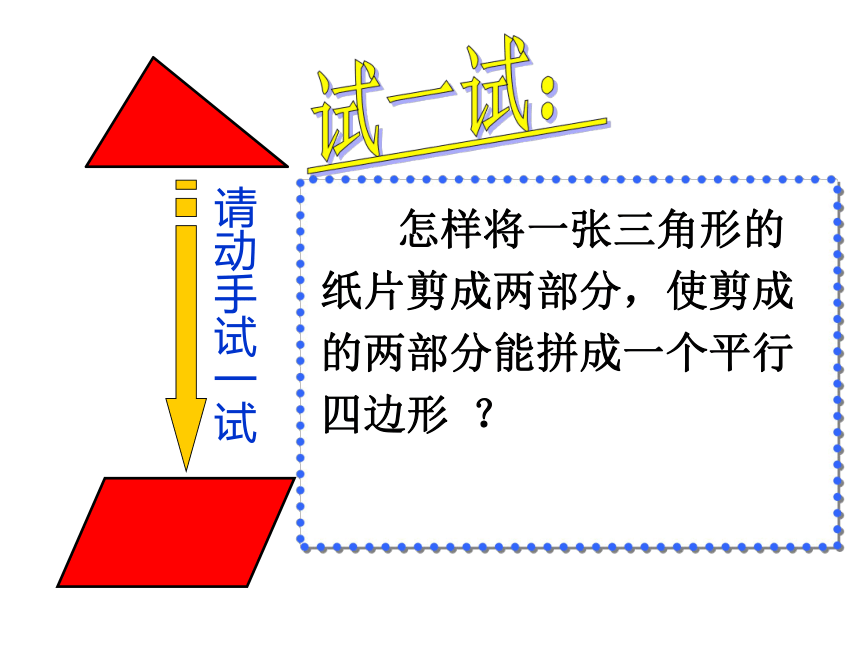
2就是AB的距离。你知道为什么吗?请动手试一试试一试: 怎样将一张三角形的纸片剪成两部分,使剪成的两部分能拼成一个平行四边形 ?
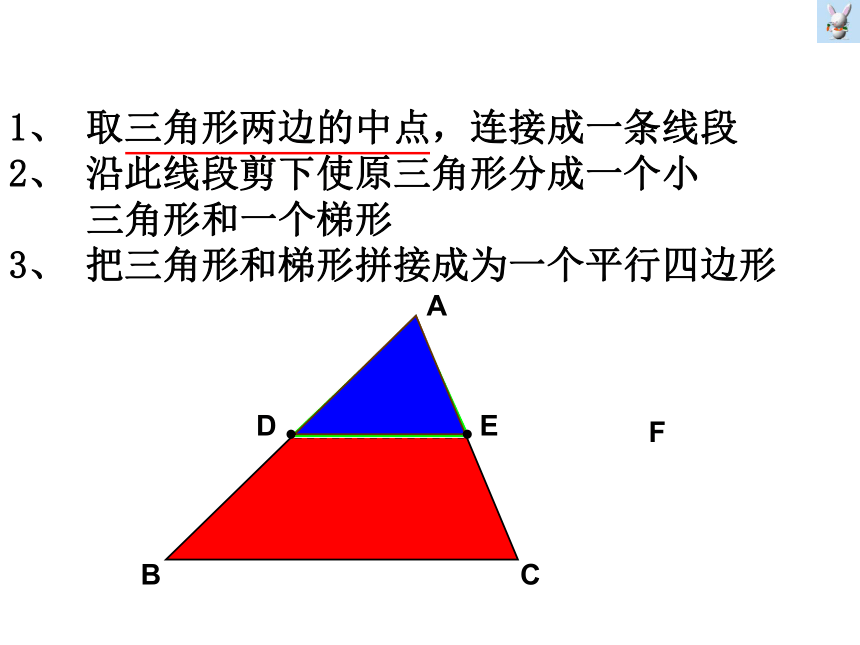
1、 取三角形两边的中点,连接成一条线段
2、 沿此线段剪下使原三角形分成一个小
三角形和一个梯形
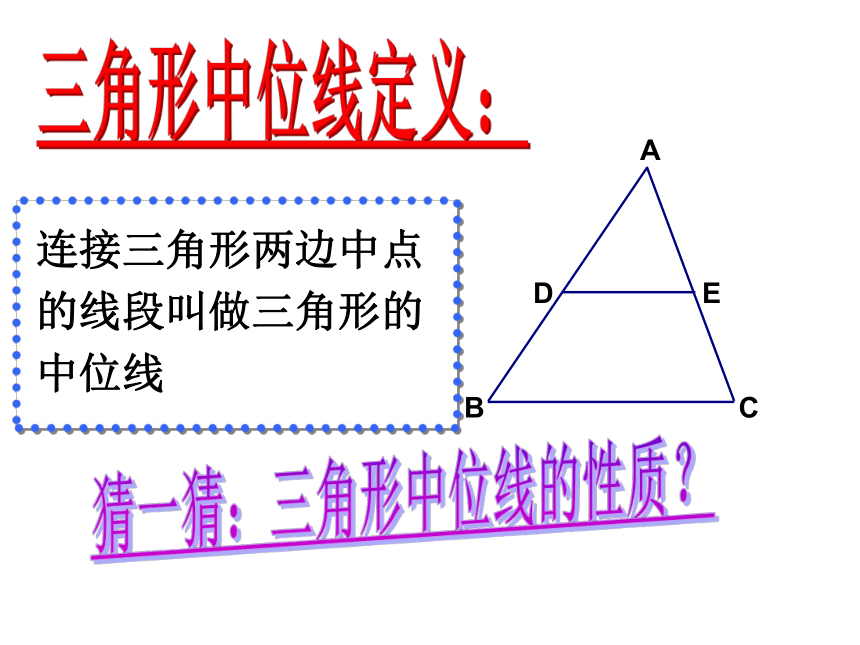
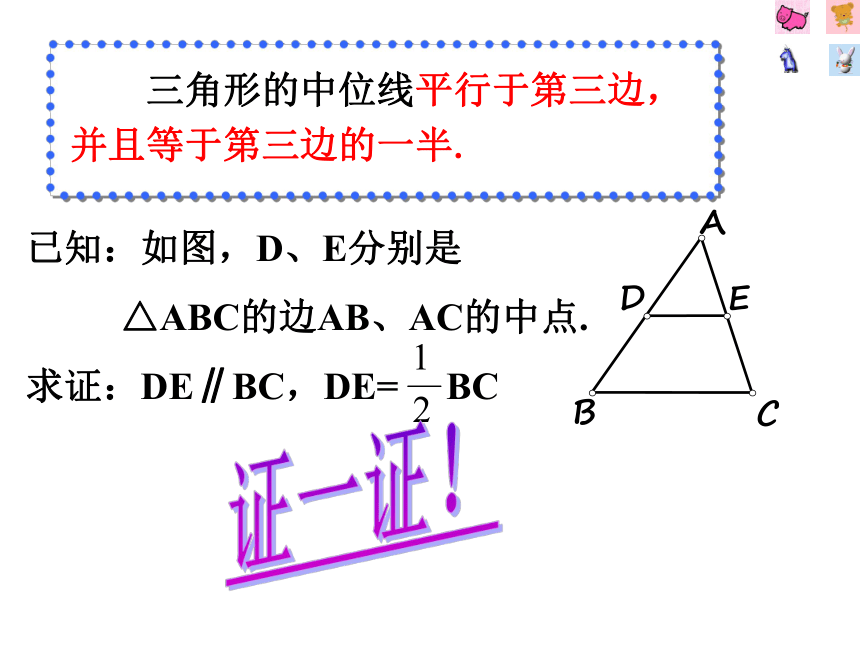
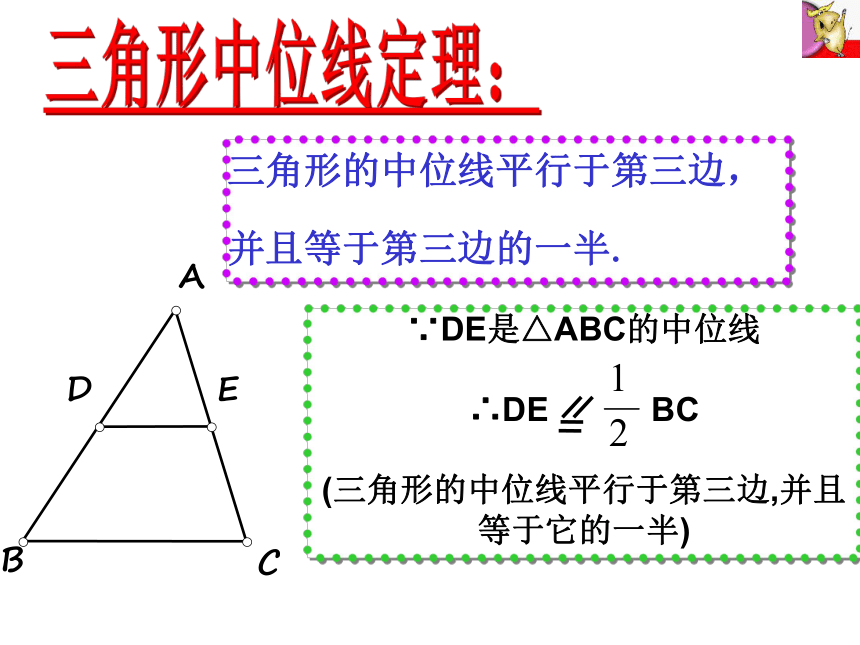
3、 把三角形和梯形拼接成为一个平行四边形ABCDEF连接三角形两边中点的线段叫做三角形的中位线三角形中位线定义:猜一猜:三角形中位线的性质? 三角形的中位线平行于第三边,并且等于第三边的一半.已知:如图,D、E分别是
△ABC的边AB、AC的中点.
求证:DE∥BC,DE= BC 证一证!∵DE是△ABC的中位线
∴DE BC
(三角形的中位线平行于第三边,并且等于它的一半)三角形的中位线平行于第三边,
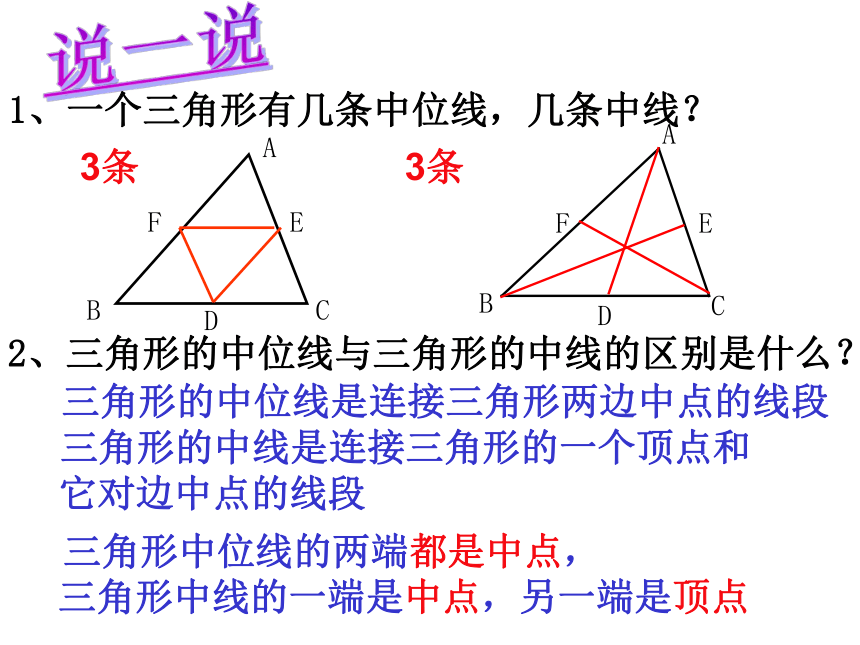
并且等于第三边的一半.三角形中位线定理:1、一个三角形有几条中位线,几条中线?BFAECD2、三角形的中位线与三角形的中线的区别是什么? 三角形中位线的两端都是中点,
三角形中线的一端是中点,另一端是顶点 三角形的中位线是连接三角形两边中点的线段
三角形的中线是连接三角形的一个顶点和
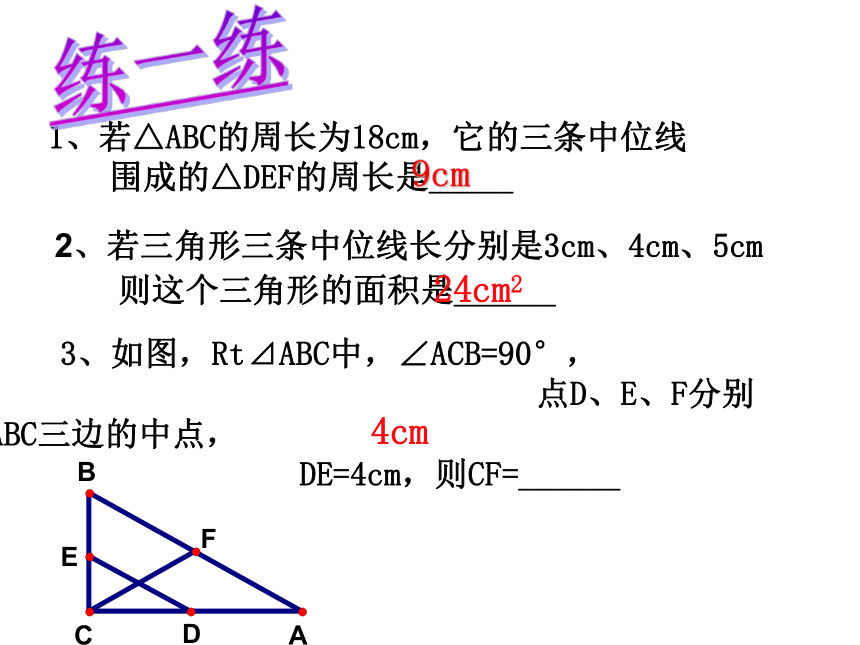
它对边中点的线段3条BCADEF说一说3条 2、若三角形三条中位线长分别是3cm、4cm、5cm
则这个三角形的面积是______ 3、如图,Rt⊿ABC中,∠ACB=90°,
点D、E、F分别是⊿ABC三边的中点,
DE=4cm,则CF=______4cm 1、若△ABC的周长为18cm,它的三条中位线
围成的△DEF的周长是_____9cm练一练24cm21、已知:如图,在⊿ABC中,D、E、F、G
分别是AC、AB、OB、OC的中点
求证:EG与DF互相平分做一做顺次连接四边形的中点所
得的四边形是平行四边形
3、已知:如图,在四边形ABCD中,
∠ABC=90°,AC=AD,点E、F分别
是CD、AC的中点,点G是BE的中点
求证:FG⊥BE 证明:连接FB、FE
∵E、F是CD、AC的中点
∴EF是⊿ACD的中位线
∴EF= AD
∵ ∠ABC=90°
∴BF= AC
∵AC=AD
∴BF=EF
∵ G是BE的中点
∴ FG⊥BE 三角形三条中位线围成一个新的三角形,它与原来的三角形有什么关系?(1) △DEF的周长与△ABC的周长有什么关系?(2) △DEF的面积与△ABC的面积有什么关系?想一想 已知:△ABC的周长为C,面积为S,
连接各边中点得△A1B1C1,再连接
△A1B1C1各边中点得△A2B2C2 ……,
则(1 ) 第2次连接所得
△A2B2C2的周长=_______, 面积=_______
(2) 第3次连接所得
△A3B3C3的周长=_______, 面积=_______
(3) 第n次连接所得
△AnBnCn的周长=_______, 面积=_______
ABCA1B1C1
A2B2C2分析:填表sccccss123ncss………………C C SS谈一谈这节课的收获吧! 连接任意四边形各边中点所成的
四边形是平行四边形.思考:改变四边形ABCD的形状,其它条件不变,
□ EFGH的形状会有什么变化?2、四边形ABCD是矩形3、四边形ABCD是菱形4、四边形ABCD是正方形5、四边形ABCD是梯形6、四边形ABCD是等腰梯形1、四边形ABCD是平行四边形7、四边形ABCD是对角线互相垂直的四边形8、四边形ABCD是对角线相等的四边形9、四边形ABCD是对角线互相垂直且相等的四边形CEDFBA 证明: 延长DE至F,使EF=DE,连结CF
在⊿AED和⊿CEF中
∵ AE=CE(已知)
∠AED=∠CEF(对顶角相等)
DE=EF(已作)
∴ ⊿AED≌⊿CEF(S.A.S)
∴AD=CF(全等三角形的对应边相等)
∠ADE=∠F (全等三角形的对应角相等)
∴AD∥CF(内错角相等,两直线平行)
∵AD=DB(已知)
∴DB=CF(等量代换)
∴四边形BCFD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
∴DF BC(平行四边形的对边平行且相等)∴DE ∥BC
∵DE= DF (已作)
∴DE= BC(等量代换)已知:如图,D、E分别是 △ABC的边AB、AC的中点.
求证:DE∥BC,DE= BC CEDFBA证明:过点C作AB的平行线交DE
的延长于点F
∵CF∥AB,
∴∠A=∠ECF
又AE=EC,∠AED=∠CEF
∴△ADE≌△CFE
∴ AD=FC,DE=EF
又DB=AD,
∴DB = FC,又∵DB ∥FC
∴四边形BCFD是平行四边形
∴DF BC
∴DE BC已知:如图,D、E分别是 △ABC的边AB、AC的中点.
求证:DE∥BC, DE= BC CEDFBA证明:以点E为旋转中心,把⊿ADE
绕点E旋转180゜
得到⊿CFE,则⊿ADE ≌ ⊿CFE
∴∠A=∠ECF ∴AB ∥FC
∴ AD=FC,
又DB=AD,
∴DB = FC,又∵DB ∥FC
∴四边形BCFD是平行四边形
∴DF BC
∵DE=EF
∴DE BC已知:如图,D、E分别是 △ABC的边AB、AC的中点.
求证:DE∥BC, DE= BC
距离,只要在池塘外取一点C,连接CA、CB,
取CA的中点E,CB的中点D,测出ED的距离乘以
2就是AB的距离。你知道为什么吗?请动手试一试试一试: 怎样将一张三角形的纸片剪成两部分,使剪成的两部分能拼成一个平行四边形 ?
1、 取三角形两边的中点,连接成一条线段
2、 沿此线段剪下使原三角形分成一个小
三角形和一个梯形
3、 把三角形和梯形拼接成为一个平行四边形ABCDEF连接三角形两边中点的线段叫做三角形的中位线三角形中位线定义:猜一猜:三角形中位线的性质? 三角形的中位线平行于第三边,并且等于第三边的一半.已知:如图,D、E分别是
△ABC的边AB、AC的中点.
求证:DE∥BC,DE= BC 证一证!∵DE是△ABC的中位线
∴DE BC
(三角形的中位线平行于第三边,并且等于它的一半)三角形的中位线平行于第三边,
并且等于第三边的一半.三角形中位线定理:1、一个三角形有几条中位线,几条中线?BFAECD2、三角形的中位线与三角形的中线的区别是什么? 三角形中位线的两端都是中点,
三角形中线的一端是中点,另一端是顶点 三角形的中位线是连接三角形两边中点的线段
三角形的中线是连接三角形的一个顶点和
它对边中点的线段3条BCADEF说一说3条 2、若三角形三条中位线长分别是3cm、4cm、5cm
则这个三角形的面积是______ 3、如图,Rt⊿ABC中,∠ACB=90°,
点D、E、F分别是⊿ABC三边的中点,
DE=4cm,则CF=______4cm 1、若△ABC的周长为18cm,它的三条中位线
围成的△DEF的周长是_____9cm练一练24cm21、已知:如图,在⊿ABC中,D、E、F、G
分别是AC、AB、OB、OC的中点
求证:EG与DF互相平分做一做顺次连接四边形的中点所
得的四边形是平行四边形
3、已知:如图,在四边形ABCD中,
∠ABC=90°,AC=AD,点E、F分别
是CD、AC的中点,点G是BE的中点
求证:FG⊥BE 证明:连接FB、FE
∵E、F是CD、AC的中点
∴EF是⊿ACD的中位线
∴EF= AD
∵ ∠ABC=90°
∴BF= AC
∵AC=AD
∴BF=EF
∵ G是BE的中点
∴ FG⊥BE 三角形三条中位线围成一个新的三角形,它与原来的三角形有什么关系?(1) △DEF的周长与△ABC的周长有什么关系?(2) △DEF的面积与△ABC的面积有什么关系?想一想 已知:△ABC的周长为C,面积为S,
连接各边中点得△A1B1C1,再连接
△A1B1C1各边中点得△A2B2C2 ……,
则(1 ) 第2次连接所得
△A2B2C2的周长=_______, 面积=_______
(2) 第3次连接所得
△A3B3C3的周长=_______, 面积=_______
(3) 第n次连接所得
△AnBnCn的周长=_______, 面积=_______
ABCA1B1C1
A2B2C2分析:填表sccccss123ncss………………C C SS谈一谈这节课的收获吧! 连接任意四边形各边中点所成的
四边形是平行四边形.思考:改变四边形ABCD的形状,其它条件不变,
□ EFGH的形状会有什么变化?2、四边形ABCD是矩形3、四边形ABCD是菱形4、四边形ABCD是正方形5、四边形ABCD是梯形6、四边形ABCD是等腰梯形1、四边形ABCD是平行四边形7、四边形ABCD是对角线互相垂直的四边形8、四边形ABCD是对角线相等的四边形9、四边形ABCD是对角线互相垂直且相等的四边形CEDFBA 证明: 延长DE至F,使EF=DE,连结CF
在⊿AED和⊿CEF中
∵ AE=CE(已知)
∠AED=∠CEF(对顶角相等)
DE=EF(已作)
∴ ⊿AED≌⊿CEF(S.A.S)
∴AD=CF(全等三角形的对应边相等)
∠ADE=∠F (全等三角形的对应角相等)
∴AD∥CF(内错角相等,两直线平行)
∵AD=DB(已知)
∴DB=CF(等量代换)
∴四边形BCFD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
∴DF BC(平行四边形的对边平行且相等)∴DE ∥BC
∵DE= DF (已作)
∴DE= BC(等量代换)已知:如图,D、E分别是 △ABC的边AB、AC的中点.
求证:DE∥BC,DE= BC CEDFBA证明:过点C作AB的平行线交DE
的延长于点F
∵CF∥AB,
∴∠A=∠ECF
又AE=EC,∠AED=∠CEF
∴△ADE≌△CFE
∴ AD=FC,DE=EF
又DB=AD,
∴DB = FC,又∵DB ∥FC
∴四边形BCFD是平行四边形
∴DF BC
∴DE BC已知:如图,D、E分别是 △ABC的边AB、AC的中点.
求证:DE∥BC, DE= BC CEDFBA证明:以点E为旋转中心,把⊿ADE
绕点E旋转180゜
得到⊿CFE,则⊿ADE ≌ ⊿CFE
∴∠A=∠ECF ∴AB ∥FC
∴ AD=FC,
又DB=AD,
∴DB = FC,又∵DB ∥FC
∴四边形BCFD是平行四边形
∴DF BC
∵DE=EF
∴DE BC已知:如图,D、E分别是 △ABC的边AB、AC的中点.
求证:DE∥BC, DE= BC
