22.6(1) 三角形的中位线 课件(20张PPT)
文档属性
| 名称 | 22.6(1) 三角形的中位线 课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 00:00:00 | ||
图片预览


文档简介
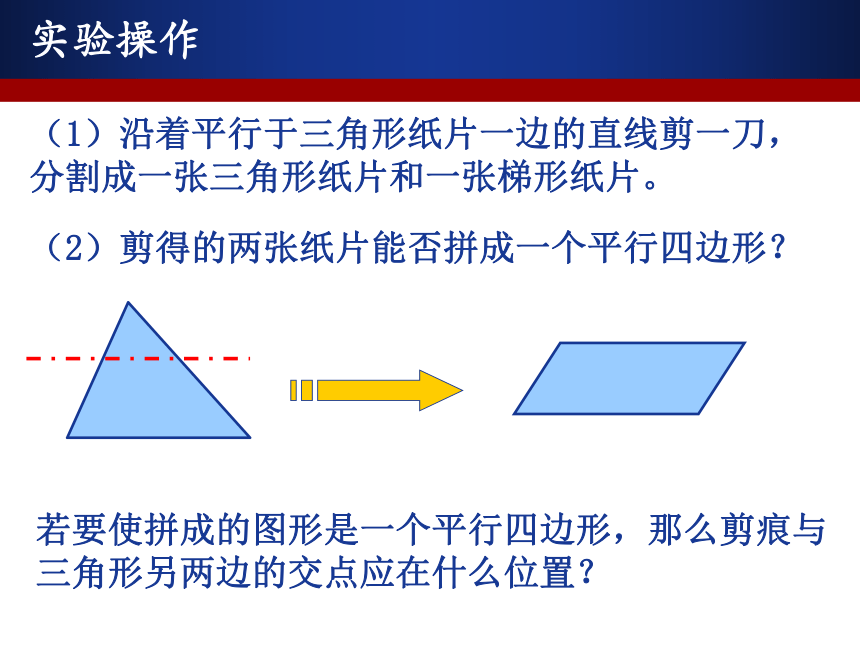
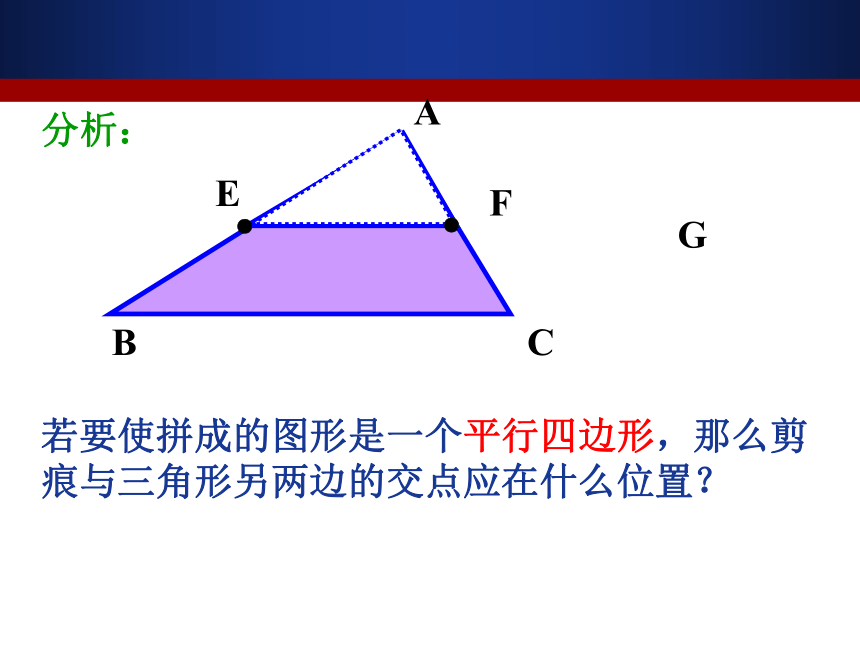
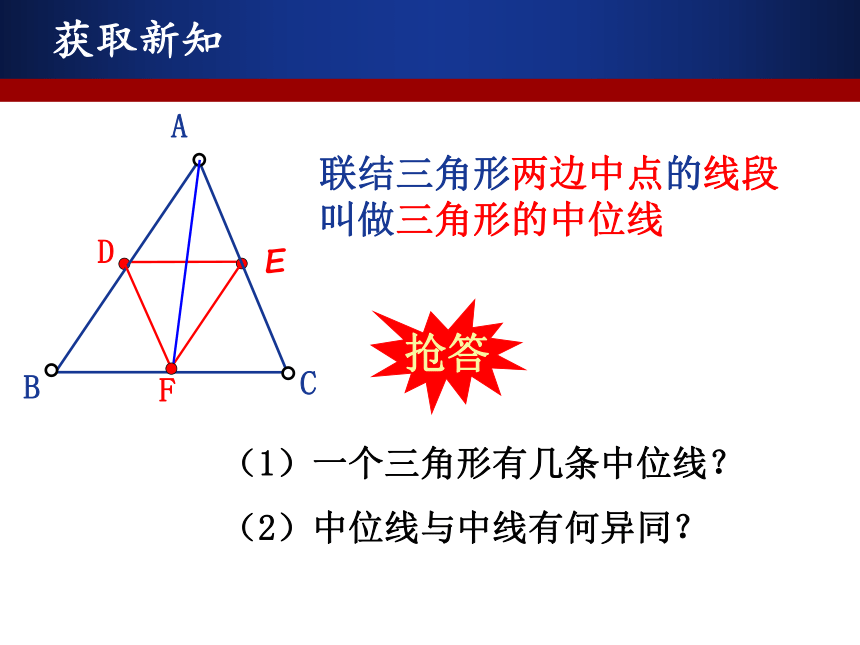
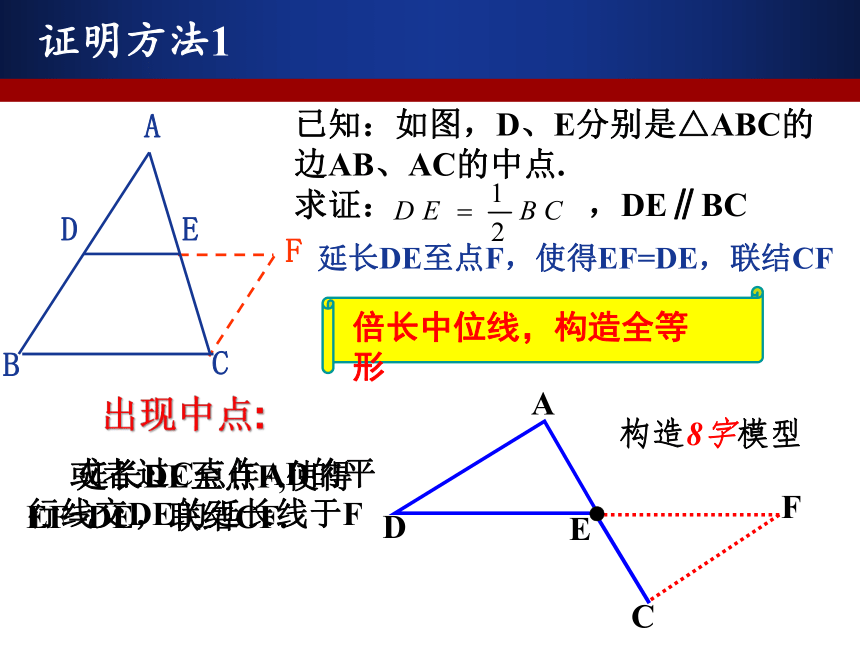
课件20张PPT。22.6 三角形的中位线问题引入(1)沿着平行于三角形纸片一边的直线剪一刀,分割成一张三角形纸片和一张梯形纸片。(2)剪得的两张纸片能否拼成一个平行四边形?若要使拼成的图形是一个平行四边形,那么剪痕与三角形另两边的交点应在什么位置?实验操作分析:●●若要使拼成的图形是一个平行四边形,那么剪痕与三角形另两边的交点应在什么位置?获取新知联结三角形两边中点的线段叫做三角形的中位线(1)一个三角形有几条中位线?
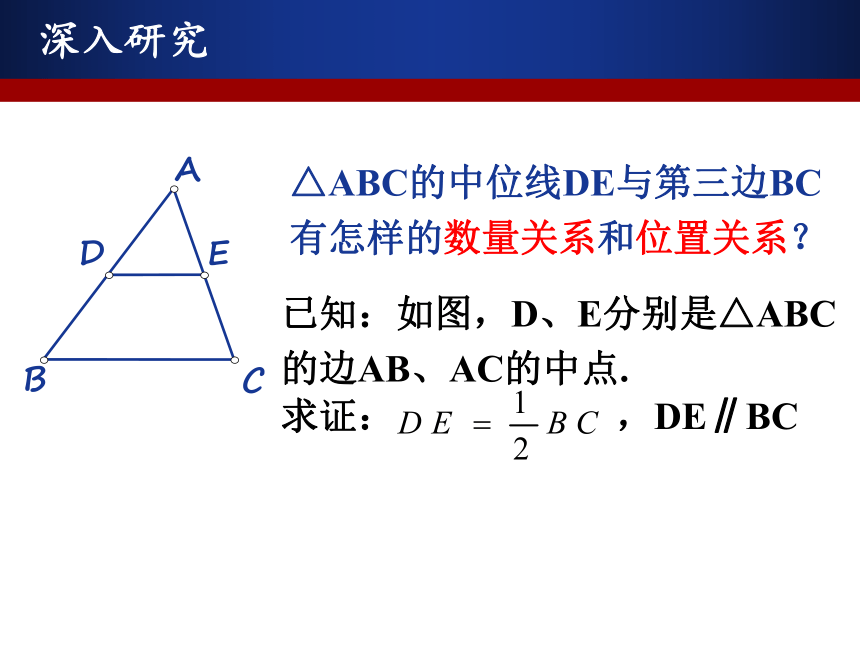
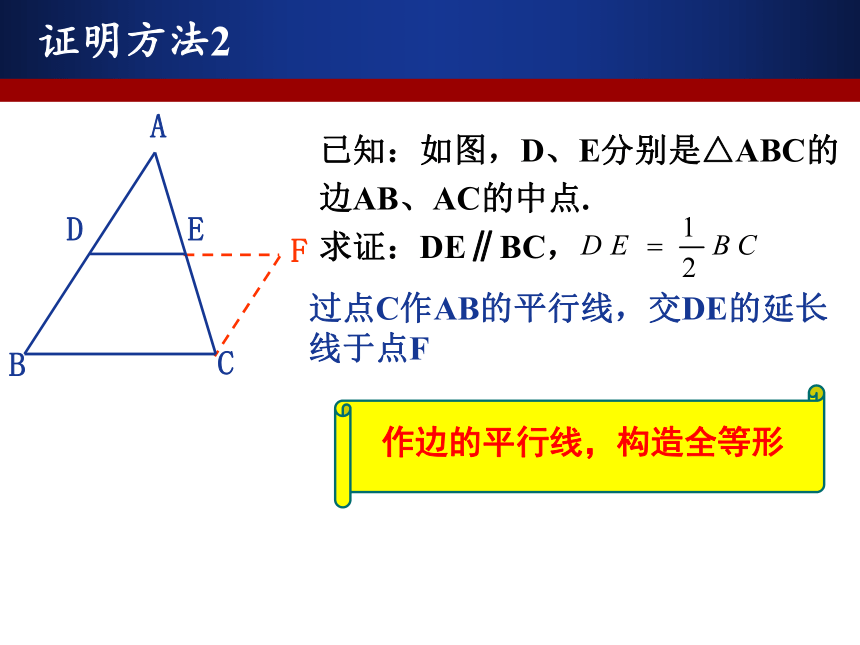
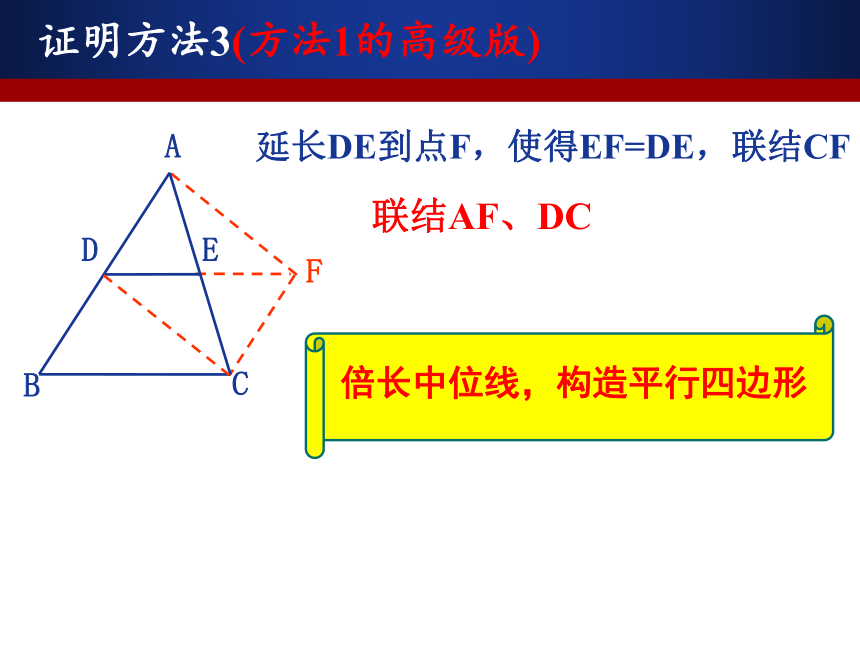
(2)中位线与中线有何异同?抢答EDF深入研究△ABC的中位线DE与第三边BC有怎样的数量关系和位置关系?证明方法1延长DE至点F,使得EF=DE,联结CFFBCEDA 或者过C点作AD的平行线交DE的延长线于F出现中点:F构造8字模型● 延长DE至点F,使得EF=DE,联结CF.证明方法2过点C作AB的平行线,交DE的延长线于点FFBCEDA证明方法3(方法1的高级版)FBCED延长DE到点F,使得EF=DE,联结CFA联结AF、DC证明方法4(欧式面积法)BCEDA∵AD=BD,AE=EC证明方法4(欧式面积法)BCEDAMN∵AD=BD,AE=EC∴S△ADE=S△BDE, S△ADE=S△CDE∴S△BDE=S△CDE过点B、C分别作BM⊥DE,CN⊥DE21∴BM∥CN,BM=CN∴四边形BCNM是平行四边形∴DE∥BC∴∠1=∠2=90°,总结提炼三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半. 在△ABC中,
∵点D、E分别是AB与AC的中点,∴符号语言:三角形的中位线与第三边的关系:初显身手如图,已知△ABC,D、E、F分别是BC、AB、AC边上的中点。(1)若∠AEF=60°,则∠B= 度(2)若BC=8cm,则EF= cm(4)若△ABC的面积为S,则△DEF的面积_____;(3)若△ABC的周长为18cm,则△DEF的周长是______;图中有_____个平行四边形;
6049cm3DA●●B● CE●●●●初步运用例题讲解例1 如图,点O是△ABC内任意一点,D、E、F、G分别是AO、CO、BC、AB的中点,
求证:四边形DEFG是平行四边形。巩固练习如图,顺次联结四边形ABCD四边的中点E、F、G、H,试说明四边形EFGH的形状。
(1) 若AC=BD,
四边形EFGH是什么图形?如图,顺次联结四边形ABCD四边的中点E、F、G、H,变式演练(2) 若AC⊥BD,
四边形EFGH是什么图形?(3) 若AC=BD且 AC⊥BD,
四边形EFGH是什么图形?谈谈收获在这节课上,你学会了什么?3、辅助线的添加方法8字中位线定理A字一个中点两个中点构造几何模型证全等1、三角形的中位线定义2、三角形的中位线定理及用途布置作业1、练习册22.6(1)(2)当∠A=90°时,试说明DE与AF有何关系?如图,已知△ABC中,D、E、F分别是BC、AB、AC边上的中点。拓展延伸(1)试说明DE与AF有何关系?(3)当AB=AC时,试说明DE与AF有何关系?
(2)中位线与中线有何异同?抢答EDF深入研究△ABC的中位线DE与第三边BC有怎样的数量关系和位置关系?证明方法1延长DE至点F,使得EF=DE,联结CFFBCEDA 或者过C点作AD的平行线交DE的延长线于F出现中点:F构造8字模型● 延长DE至点F,使得EF=DE,联结CF.证明方法2过点C作AB的平行线,交DE的延长线于点FFBCEDA证明方法3(方法1的高级版)FBCED延长DE到点F,使得EF=DE,联结CFA联结AF、DC证明方法4(欧式面积法)BCEDA∵AD=BD,AE=EC证明方法4(欧式面积法)BCEDAMN∵AD=BD,AE=EC∴S△ADE=S△BDE, S△ADE=S△CDE∴S△BDE=S△CDE过点B、C分别作BM⊥DE,CN⊥DE21∴BM∥CN,BM=CN∴四边形BCNM是平行四边形∴DE∥BC∴∠1=∠2=90°,总结提炼三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半. 在△ABC中,
∵点D、E分别是AB与AC的中点,∴符号语言:三角形的中位线与第三边的关系:初显身手如图,已知△ABC,D、E、F分别是BC、AB、AC边上的中点。(1)若∠AEF=60°,则∠B= 度(2)若BC=8cm,则EF= cm(4)若△ABC的面积为S,则△DEF的面积_____;(3)若△ABC的周长为18cm,则△DEF的周长是______;图中有_____个平行四边形;
6049cm3DA●●B● CE●●●●初步运用例题讲解例1 如图,点O是△ABC内任意一点,D、E、F、G分别是AO、CO、BC、AB的中点,
求证:四边形DEFG是平行四边形。巩固练习如图,顺次联结四边形ABCD四边的中点E、F、G、H,试说明四边形EFGH的形状。
(1) 若AC=BD,
四边形EFGH是什么图形?如图,顺次联结四边形ABCD四边的中点E、F、G、H,变式演练(2) 若AC⊥BD,
四边形EFGH是什么图形?(3) 若AC=BD且 AC⊥BD,
四边形EFGH是什么图形?谈谈收获在这节课上,你学会了什么?3、辅助线的添加方法8字中位线定理A字一个中点两个中点构造几何模型证全等1、三角形的中位线定义2、三角形的中位线定理及用途布置作业1、练习册22.6(1)(2)当∠A=90°时,试说明DE与AF有何关系?如图,已知△ABC中,D、E、F分别是BC、AB、AC边上的中点。拓展延伸(1)试说明DE与AF有何关系?(3)当AB=AC时,试说明DE与AF有何关系?
