人教版九年级下册数学27.1 图形的相似同步练习(含解析)
文档属性
| 名称 | 人教版九年级下册数学27.1 图形的相似同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 826.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 09:45:44 | ||
图片预览

文档简介
27.1 图形的相似
基础闯关全练
1.观察下列每组图形,相似图形是 ( )
A. B. C. D.
2.对一个图形进行放缩时,下列说法中正确的是( )
A.图形中线段的长度与角的大小都保持不变
B.图形中线段的长度与角的大小都会改变
C.图形中线段的长度保持不变,角的大小改变
D.图形中线段的长度改变,角的大小保持不变
3.下列说法正确的是( )
A.任意两个等腰三角形都相似
B.任意两个菱形都相似
C.任意两个正五边形都相似
D.对应角相等的两个多边形相似
4.已知线段a、b、c、d,如果ab=cd,那么下列式子中一定正确的是 ( )
A. B. C. D.
5.已知四条线段a,b,c,d成比例,并且a=2,b=,c=,则d=________.
6.如果A、B两地的实际距离是20 km.且A、B两点在地图上的距离是4 cm,那么实际距离是500 km的两地在地图上的距离是____cm.
7.若如图所示的两个四边形相似,则∠α的度数是 ( )
A.87? B.60? C.75? D.120?
8.在如图的网格中画出四边形ABCD的相似图形.(提示:不能画成全等图形)
能力提升全练
1.如图,把一个矩形划分为5个全等的小矩形,若要使小矩形与原矩形相似,则原矩形的边a、b应满足的条件是 ( )
A.a=5b B.a=10b C.a=b D.a=2b
2.如图所示,一般书本的纸张是由原纸张多次对开得到的,矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,依次类推,若各种开本的矩形都相似,则等于 ( )
A.0.618 B. C. D.2
3.如图,内外两个四边形相似,且对应边互相平行,则下列结论正确的是( )
A. B. C. D.以上均不正确
4.如图27 -1-6,点E,F分别是矩形ABCD的边AD,BC的三等分点(分别靠近于D、C),若矩形ABFE与矩形ADCB相似,则AD:AB的值为_______.
三年模拟全练
1.下列图形一定是相似图形的是 ( )
A.两个矩形 B.两个等腰三角形
C.两个直角三角形 D.两个正方形
2.如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点处,若四边形EFDC与矩形ABCD相似,则AD= ( )
A. B.+1 C.4 D.2
3.在比例尺是1:15000000的地图上,测得甲乙两地的距离是2 cm,那么甲乙两地的实际距离是______km.
五年中考全练
1.已知(a≠0,b≠0),下列变形错误的是 ( )
A. B.2a=3b C. D.3a=2b
2.把标准纸一次又一次对开,可以得到均相似的“开纸”,现在我们在长为2、宽为1的矩形纸片中,画两个小矩形,使这两个小矩形的每条边都与原矩形纸的边平行,或小矩形的边在原矩形纸的边上,且每个小矩形均与原矩形纸相似,然后将它们剪下,则所剪得的两个小矩形纸片周长之和的最大值是_________.
核心素养全练
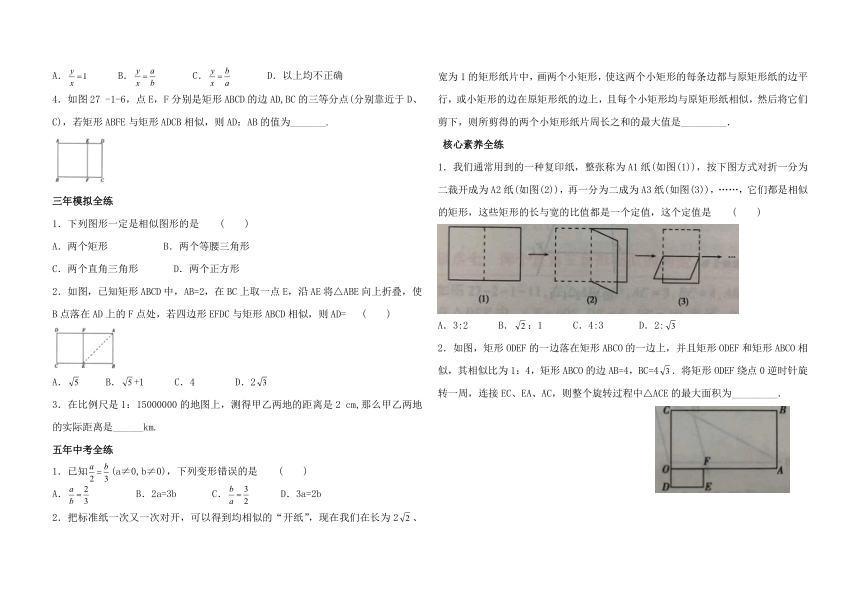
1.我们通常用到的一种复印纸,整张称为A1纸(如图(1)),按下图方式对折一分为二裁开成为A2纸(如图(2)),再一分为二成为A3纸(如图(3)),……,它们都是相似的矩形,这些矩形的长与宽的比值都是一个定值,这个定值是 ( )
A.3:2 B.:1 C.4:3 D.2:
如图,矩形ODEF的一边落在矩形ABCO的一边上,并且矩形ODEF和矩形ABCO相似,其相似比为1:4,矩形ABCO的边AB=4,BC=4.将矩形ODEF绕点0逆时针旋转一周,连接EC、EA、AC,则整个旋转过程中△ACE的最大面积为_________.
第二十七章 相似
27.1 图形的相似
1.D A项,两图形形状不同,故不是相似图形;B项,两图形形状不同,故不是相似图形;C项,两图形形状不同,故不是相似图形:D项,两图形形状相同,故是相似图形.故选D.
2.D根据相似多边形的性质:相似多边形的对应边成比例,对应角相等,∴对一个图形进行放缩时,图形中线段的长度改变,角的大小保持不变,故选D.
3.C选项A,任意两个等腰三角形都相似,错误;选项B,任意两个菱形都相似,错误;选项C,任意两个正五边形都相似,正确:选项D,对应角相等的两个多边形相似,错误.故选C.
4.C ∵ab=cd,∴.故选C.
5.答案
解析由题意得2::d,解得d=.
6.答案100
解析设两地在地图上的距离是xcm,则4:2000000=x:50000000.解得x=100.
7.A如图,∵两个四边形相似,
∴∠1=138?,
∵四边形的内角和等于360?.
∴∠α=360?-60?-75?-138?=87?.故选A.
8.解析如图,四边形A′B′C′D′就是所求.(答案不唯一)
I.C ∵小矩形与原矩形相似,∴,∴a?=5b?,∴a=b,故选C.
2.C 由题意得,且AE=AD,∴AB?=AD?,即()?=2,∴.故选C.
3.B ∵题图内外两个四边形相似∴对应边的比相等,∴,∴a(b-2x)=b(a-2y),即ab-2ax=ab-2by,∴ax=by,
∴,故选B.
4.答案
解析设DE=x(x>0),AE=2x,则AD=3x,∴矩形ABFE与矩形ADCB相似,∴,∴AB?=6x?,∴AB=,∴AD:AB=(3x):()=,
一、选择题
1.D A项,两个矩形,角对应相等,边不一定对应成比例,故不符合题意;B项,两个等腰三角形顶角不一定对应相等,故不符合题意;C项,两个直角三角形,只有一个直角相同,锐角不一定对应相等,故不符合题意;D项,两个正方形,形状相同,角分别相等,边成比例,符合相似多边形定义,故符合题意,故选D.
2.B∵沿AE将△ABE向上折叠,使B点落在AD上的F点,∴四边形ABEF是正方形,设AD=x(x>0),∴AB=2,∴FD=x-2,FE=2,∵四边形EFDC与矩形ABCD相似,∴,即,解得x?=1+,x?=1-(负值舍去),经检验,x=1+是原方程的解.故选B.
二、填空题
3.答案300
解析设甲乙两地的实际距离是x cm,根据题意得,解得结果x=30 000 000,
∵30 000 000 cm=300 km,
∴甲乙两地的实际距离是300 km.
4.答案20
解析∵两个四边形相似,一个四边形的各边之比为1:2:3:4,∴和它相似的另一个四边形的对应边的比为1:2:3:4.∵另一个四边形的最小边长为5 cm,∴最大边长为4×5=20 cm.
一、选择题
1.B由得3a=2b.A项,由可得3a=2b,变形正确;B项,变形错误;C项,由得3a=2b,变形正确;D项,变形正确.故选B.
二、填空题
2.答案
解析要使所剪得的两个小矩形纸片周长之和最大,则这两个小矩形纸片的长与宽的和最大,所以应按如图所示方式剪纸.
设AF=x,CH=y.
∵矩形BEFA和矩形CHGE均与矩形ABCD相似,
∴,
∵AB=1,AD=2,
∴,
∴x=,y=,
∴周长之和的最大值是2.
1.B设原矩形的长为a,宽为b,根据相似多边形的性质可知,
,解得a=b,矩形的长与宽的比值为:1,故选B.
2
2.答案8+8
解析连接OE,∵矩形ODEF和矩形ABCO相似,其相似比为1:4,矩形ABCO的边AB=4,BC=4,
∴OF= ,OD=1,
∴OE==2,
∴点E的轨迹是以点0为圆心,2为半径的圆,
设点O到线段AC的距离为h,易知AC==8,
∴8h=4×4.解得h=2,
∴当点E到AC的距离为2+2时,△ACE的面积最大,
.
基础闯关全练
1.观察下列每组图形,相似图形是 ( )
A. B. C. D.
2.对一个图形进行放缩时,下列说法中正确的是( )
A.图形中线段的长度与角的大小都保持不变
B.图形中线段的长度与角的大小都会改变
C.图形中线段的长度保持不变,角的大小改变
D.图形中线段的长度改变,角的大小保持不变
3.下列说法正确的是( )
A.任意两个等腰三角形都相似
B.任意两个菱形都相似
C.任意两个正五边形都相似
D.对应角相等的两个多边形相似
4.已知线段a、b、c、d,如果ab=cd,那么下列式子中一定正确的是 ( )
A. B. C. D.
5.已知四条线段a,b,c,d成比例,并且a=2,b=,c=,则d=________.
6.如果A、B两地的实际距离是20 km.且A、B两点在地图上的距离是4 cm,那么实际距离是500 km的两地在地图上的距离是____cm.
7.若如图所示的两个四边形相似,则∠α的度数是 ( )
A.87? B.60? C.75? D.120?
8.在如图的网格中画出四边形ABCD的相似图形.(提示:不能画成全等图形)
能力提升全练
1.如图,把一个矩形划分为5个全等的小矩形,若要使小矩形与原矩形相似,则原矩形的边a、b应满足的条件是 ( )
A.a=5b B.a=10b C.a=b D.a=2b
2.如图所示,一般书本的纸张是由原纸张多次对开得到的,矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,依次类推,若各种开本的矩形都相似,则等于 ( )
A.0.618 B. C. D.2
3.如图,内外两个四边形相似,且对应边互相平行,则下列结论正确的是( )
A. B. C. D.以上均不正确
4.如图27 -1-6,点E,F分别是矩形ABCD的边AD,BC的三等分点(分别靠近于D、C),若矩形ABFE与矩形ADCB相似,则AD:AB的值为_______.
三年模拟全练
1.下列图形一定是相似图形的是 ( )
A.两个矩形 B.两个等腰三角形
C.两个直角三角形 D.两个正方形
2.如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点处,若四边形EFDC与矩形ABCD相似,则AD= ( )
A. B.+1 C.4 D.2
3.在比例尺是1:15000000的地图上,测得甲乙两地的距离是2 cm,那么甲乙两地的实际距离是______km.
五年中考全练
1.已知(a≠0,b≠0),下列变形错误的是 ( )
A. B.2a=3b C. D.3a=2b
2.把标准纸一次又一次对开,可以得到均相似的“开纸”,现在我们在长为2、宽为1的矩形纸片中,画两个小矩形,使这两个小矩形的每条边都与原矩形纸的边平行,或小矩形的边在原矩形纸的边上,且每个小矩形均与原矩形纸相似,然后将它们剪下,则所剪得的两个小矩形纸片周长之和的最大值是_________.
核心素养全练
1.我们通常用到的一种复印纸,整张称为A1纸(如图(1)),按下图方式对折一分为二裁开成为A2纸(如图(2)),再一分为二成为A3纸(如图(3)),……,它们都是相似的矩形,这些矩形的长与宽的比值都是一个定值,这个定值是 ( )
A.3:2 B.:1 C.4:3 D.2:
如图,矩形ODEF的一边落在矩形ABCO的一边上,并且矩形ODEF和矩形ABCO相似,其相似比为1:4,矩形ABCO的边AB=4,BC=4.将矩形ODEF绕点0逆时针旋转一周,连接EC、EA、AC,则整个旋转过程中△ACE的最大面积为_________.
第二十七章 相似
27.1 图形的相似
1.D A项,两图形形状不同,故不是相似图形;B项,两图形形状不同,故不是相似图形;C项,两图形形状不同,故不是相似图形:D项,两图形形状相同,故是相似图形.故选D.
2.D根据相似多边形的性质:相似多边形的对应边成比例,对应角相等,∴对一个图形进行放缩时,图形中线段的长度改变,角的大小保持不变,故选D.
3.C选项A,任意两个等腰三角形都相似,错误;选项B,任意两个菱形都相似,错误;选项C,任意两个正五边形都相似,正确:选项D,对应角相等的两个多边形相似,错误.故选C.
4.C ∵ab=cd,∴.故选C.
5.答案
解析由题意得2::d,解得d=.
6.答案100
解析设两地在地图上的距离是xcm,则4:2000000=x:50000000.解得x=100.
7.A如图,∵两个四边形相似,
∴∠1=138?,
∵四边形的内角和等于360?.
∴∠α=360?-60?-75?-138?=87?.故选A.
8.解析如图,四边形A′B′C′D′就是所求.(答案不唯一)
I.C ∵小矩形与原矩形相似,∴,∴a?=5b?,∴a=b,故选C.
2.C 由题意得,且AE=AD,∴AB?=AD?,即()?=2,∴.故选C.
3.B ∵题图内外两个四边形相似∴对应边的比相等,∴,∴a(b-2x)=b(a-2y),即ab-2ax=ab-2by,∴ax=by,
∴,故选B.
4.答案
解析设DE=x(x>0),AE=2x,则AD=3x,∴矩形ABFE与矩形ADCB相似,∴,∴AB?=6x?,∴AB=,∴AD:AB=(3x):()=,
一、选择题
1.D A项,两个矩形,角对应相等,边不一定对应成比例,故不符合题意;B项,两个等腰三角形顶角不一定对应相等,故不符合题意;C项,两个直角三角形,只有一个直角相同,锐角不一定对应相等,故不符合题意;D项,两个正方形,形状相同,角分别相等,边成比例,符合相似多边形定义,故符合题意,故选D.
2.B∵沿AE将△ABE向上折叠,使B点落在AD上的F点,∴四边形ABEF是正方形,设AD=x(x>0),∴AB=2,∴FD=x-2,FE=2,∵四边形EFDC与矩形ABCD相似,∴,即,解得x?=1+,x?=1-(负值舍去),经检验,x=1+是原方程的解.故选B.
二、填空题
3.答案300
解析设甲乙两地的实际距离是x cm,根据题意得,解得结果x=30 000 000,
∵30 000 000 cm=300 km,
∴甲乙两地的实际距离是300 km.
4.答案20
解析∵两个四边形相似,一个四边形的各边之比为1:2:3:4,∴和它相似的另一个四边形的对应边的比为1:2:3:4.∵另一个四边形的最小边长为5 cm,∴最大边长为4×5=20 cm.
一、选择题
1.B由得3a=2b.A项,由可得3a=2b,变形正确;B项,变形错误;C项,由得3a=2b,变形正确;D项,变形正确.故选B.
二、填空题
2.答案
解析要使所剪得的两个小矩形纸片周长之和最大,则这两个小矩形纸片的长与宽的和最大,所以应按如图所示方式剪纸.
设AF=x,CH=y.
∵矩形BEFA和矩形CHGE均与矩形ABCD相似,
∴,
∵AB=1,AD=2,
∴,
∴x=,y=,
∴周长之和的最大值是2.
1.B设原矩形的长为a,宽为b,根据相似多边形的性质可知,
,解得a=b,矩形的长与宽的比值为:1,故选B.
2
2.答案8+8
解析连接OE,∵矩形ODEF和矩形ABCO相似,其相似比为1:4,矩形ABCO的边AB=4,BC=4,
∴OF= ,OD=1,
∴OE==2,
∴点E的轨迹是以点0为圆心,2为半径的圆,
设点O到线段AC的距离为h,易知AC==8,
∴8h=4×4.解得h=2,
∴当点E到AC的距离为2+2时,△ACE的面积最大,
.
