人教版八年级数学下册19.2.1正比例函数(2)课件(27张PPT)
文档属性
| 名称 | 人教版八年级数学下册19.2.1正比例函数(2)课件(27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 10:47:22 | ||
图片预览





文档简介
(共27张PPT)
19.2.1 正比例函数(2)
一导学
学习目标:
1.会画正比例函数的图象;
2.能根据正比例函数的图象和表达式 y =kx(k≠0)
理解k>0和k<0时,函数的图象特征与增减性;
3.通过观察图象、归纳总结概括出正比例函数性质
的活动,发展数学感知、数学表征、数学概括能
力,体会数形结合的思想,发展几何直观.
学习重难点:
重点: 感悟正比例函数的图象及画法
难点: 掌握正比例函数的性质
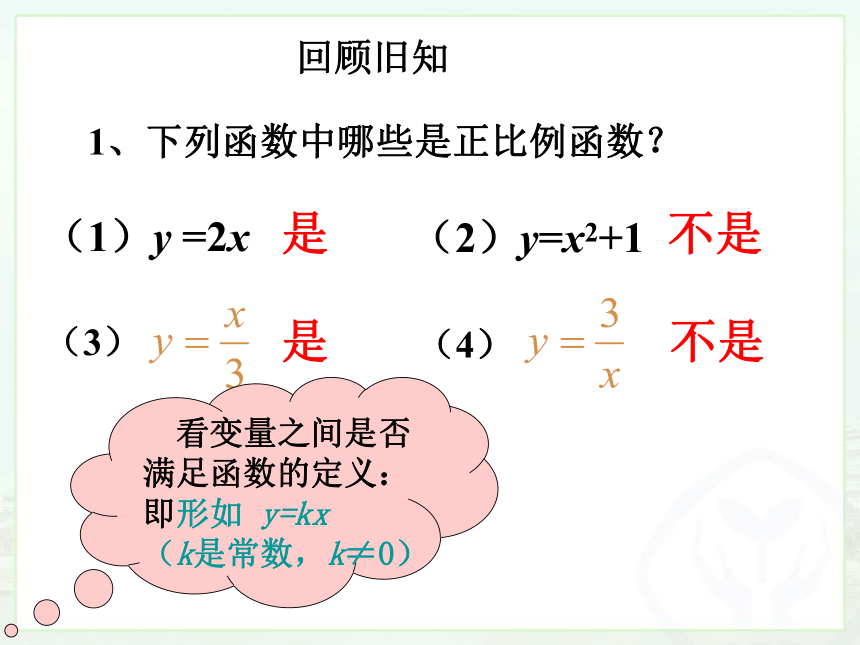
1、下列函数中哪些是正比例函数?
(1)y =2x
(2)y=x2+1
是
是
不是
不是
回顾旧知
2、若 y =5x 3m-2 是正比例函数,则 m = 。
4、
若
是正比例函数,
则 k = ( ),
此时的函数解析式为
( )
1
-2
-2
y=-4x
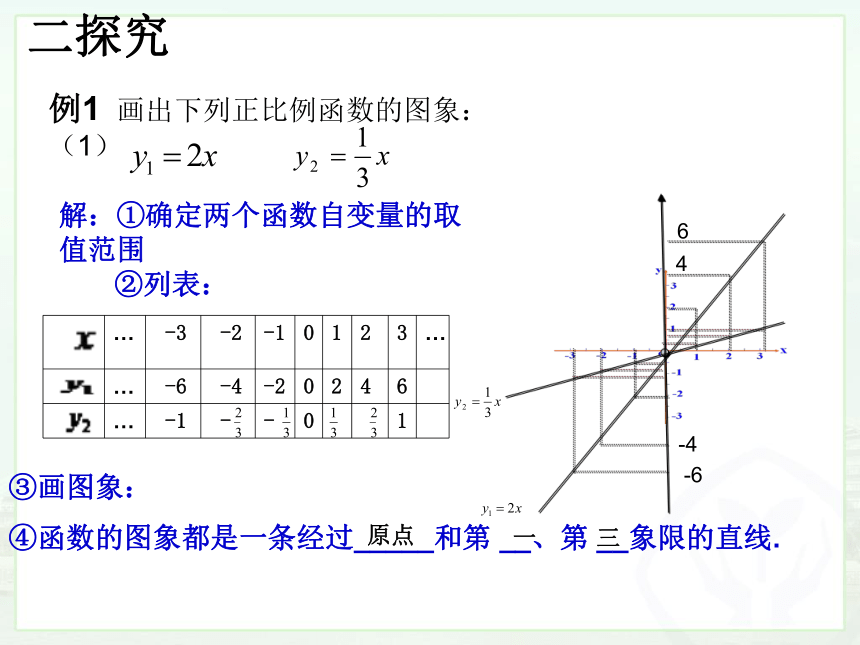
③画图象:
④函数的图象都是一条经过_____和第 __、第 __象限的直线.
原点
一 三
解:①确定两个函数自变量的取值范围
②列表:
二探究
… -3 -2 -1 0 1 2 3 …
… -6 -4 -2 0 2 4 6
… -1 - - 0 1
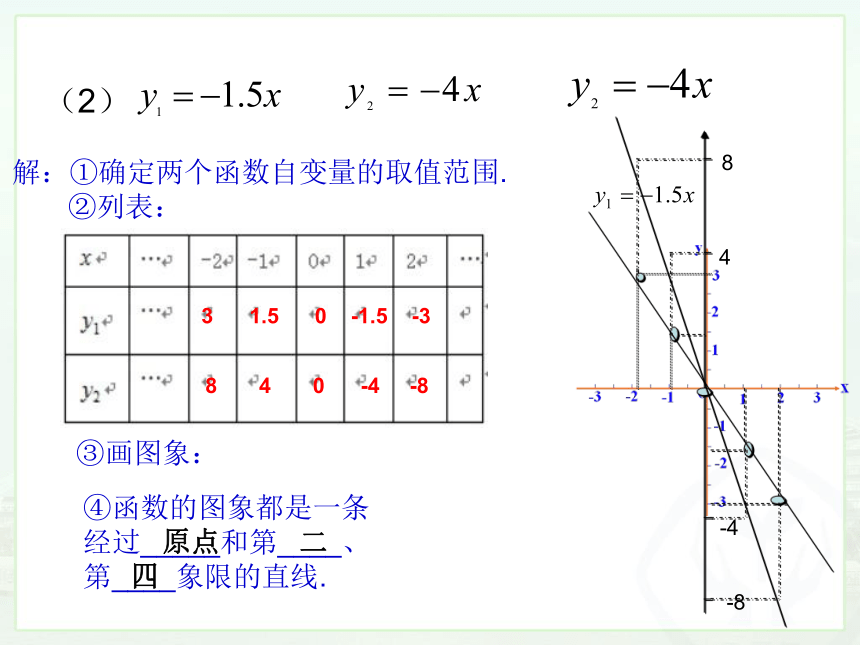
(2)
解:①确定两个函数自变量的取值范围.
②列表:
③画图象:
3 1.5 0 -1.5 -3
8 4 0 -4 -8
④函数的图象都是一条经过_____和第____、第____象限的直线.
原点 二
四
正比例函数y= kx (k≠0)
的图象是经过原点(0,0)和(1,k)的一条直线。
正比例函数性质
正比例函数y= kx (k≠0) 的图象是经过原点的一条直线。
当k>0时,直线y=kx 经过第一、三象限;
当k<0时,直线y=kx 经过第二、四象限。
(我们称它为直线y=kx)
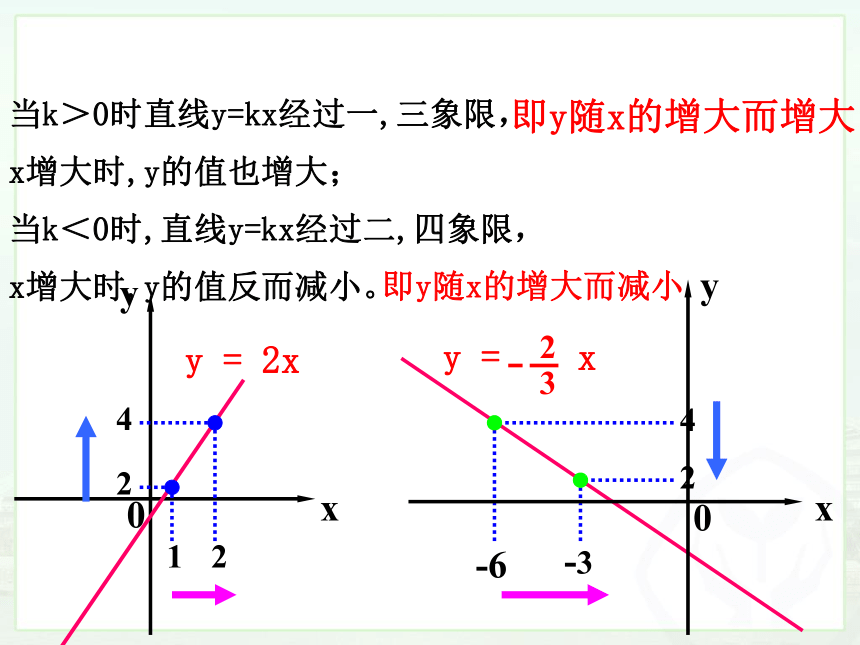
当k>0时直线y=kx经过一,三象限,
x增大时,y的值也增大;
当k<0时,直线y=kx经过二,四象限,
x增大时,y的值反而减小。
2
4
y = 2x
1
2
2
4
即y随x的增大而增大
即y随x的增大而减小
-3
-6
正比例函数y= kx (k≠0) 的图象是
当k>0时,直线y=kx 经过第一,三象限;
当k<0时,直线y=kx 经过第二、四象限。
一条经过原点的直线。
从左向右上升,即随着x的增大y也增大
从左向右下降,即随着x的增大y反而减小
1、函数y=-5x的图象过
第 象限, 经过点(0, )
与点(1, ),y随x的增大而 .
二、四
0
-5
减小
课堂练习
2、正比例函数y=(k+1)x的图象中y随x 的增大而增大,则k的取值范围是 。
k>-1
②, ④,⑤
① , ③
理由是:正比例函数 y= kx(k≠0)
⑴当k>0时,函数y随自变量x的增大而增大.
⑵当k<0时,函数y随自变量x的增大而减少 .
4.已知y与x成正比例,且x=2时,y=-6,则当x=9时,求y的值.
解:由题意设函数的解析式:y=kx(k≠0)
所以,-6 = 2k
解得:k = -3
因此,该函数的解析式为:y=-3x
当x=9时,y=-3×9=-27
1、下列函数中,是正比例函数的是( )
A、 B、
C、 D、y=2x2
B
三检测
2、在下列图像中,表示函数y=-kx
(k<0)的图像是( )
A
B
3、正比例函数y=(m-1)x的图象
经过一、三象限,则m的取值
范围是( )
A、m=1 B、m>1
C、m<1 D、m≥1
4、你能任意举出一个过第二、四
象限的正比例函数的解析式吗?
2
6、直线y=(k2+3)x经过 象限,y随x的增大而 。
一、三
增大
7、已知A(-1,y1 ),B(3, y2)都
在直线y=-5x上,则y1与y2的关系
是( )
A、 y1≤y2 B、 y1=y2
C 、y1<y2 D、 y1>y2
D
8、若正比例函数y=(1-2m)x的图像经过点A(x1,y1)和B(x2,y2),当x1<x2时,y1 >y2,则m的取值范围是 。
m>
(1)本节课,我们研究了什么,得到了哪些成果?
(2)正比例函数的图象及性质怎样?
(3)我们是怎样进行研究的?
(4)正比例函数研究过程中,你感受最深的是什么?
1.课堂小结
四 拓展
1.已知某种小汽车的耗油量是每100km耗油15升.所使用的汽油今日涨价到5元/升.
(1)写出汽车行驶途中所耗油费 y(元)与行程 x(km)之间的函数关系式;
(2)在平面直角坐标系内描出大致的函数关系图;
(3)计算娄底到长沙220 km所需油费是多少?
y/元
x/km
1 2 3 4 5 6 7 8
6
5
4
3
2
1
O
解:(1)y=5× x ,
即 .
(2)
列表
(3)当
时,
娄底到长沙220公里所需油费是165元.
描点
连线
2.知识延伸
x 0 4
y 0 3
2.汽车由A城驶往相距120km的B城,s(km)表示
汽车离开A城的距离,t(h)表示汽车行驶的
时间,如图:
⑴求汽车行驶的速度。
⑵当t=1时,
汽车离开A城有多远?
⑶当s=100时,
汽车行驶了多长时间?
t/h
0
s/km
3.比较大小:
(1)k1 k2;(2)k3 k4;
(3)比较k1, k2, k3, k4大小,并用不等号连接.
<
k1<k2 <k3 <k4
<
教科书第98页习题19.2第2题;
用简便方法画下列函数的图象,并说说当x 增
大时,函数值 y 分别怎样变化:
(1)y =4x;(2)y =-2x.
课后作业
19.2.1 正比例函数(2)
一导学
学习目标:
1.会画正比例函数的图象;
2.能根据正比例函数的图象和表达式 y =kx(k≠0)
理解k>0和k<0时,函数的图象特征与增减性;
3.通过观察图象、归纳总结概括出正比例函数性质
的活动,发展数学感知、数学表征、数学概括能
力,体会数形结合的思想,发展几何直观.
学习重难点:
重点: 感悟正比例函数的图象及画法
难点: 掌握正比例函数的性质
1、下列函数中哪些是正比例函数?
(1)y =2x
(2)y=x2+1
是
是
不是
不是
回顾旧知
2、若 y =5x 3m-2 是正比例函数,则 m = 。
4、
若
是正比例函数,
则 k = ( ),
此时的函数解析式为
( )
1
-2
-2
y=-4x
③画图象:
④函数的图象都是一条经过_____和第 __、第 __象限的直线.
原点
一 三
解:①确定两个函数自变量的取值范围
②列表:
二探究
… -3 -2 -1 0 1 2 3 …
… -6 -4 -2 0 2 4 6
… -1 - - 0 1
(2)
解:①确定两个函数自变量的取值范围.
②列表:
③画图象:
3 1.5 0 -1.5 -3
8 4 0 -4 -8
④函数的图象都是一条经过_____和第____、第____象限的直线.
原点 二
四
正比例函数y= kx (k≠0)
的图象是经过原点(0,0)和(1,k)的一条直线。
正比例函数性质
正比例函数y= kx (k≠0) 的图象是经过原点的一条直线。
当k>0时,直线y=kx 经过第一、三象限;
当k<0时,直线y=kx 经过第二、四象限。
(我们称它为直线y=kx)
当k>0时直线y=kx经过一,三象限,
x增大时,y的值也增大;
当k<0时,直线y=kx经过二,四象限,
x增大时,y的值反而减小。
2
4
y = 2x
1
2
2
4
即y随x的增大而增大
即y随x的增大而减小
-3
-6
正比例函数y= kx (k≠0) 的图象是
当k>0时,直线y=kx 经过第一,三象限;
当k<0时,直线y=kx 经过第二、四象限。
一条经过原点的直线。
从左向右上升,即随着x的增大y也增大
从左向右下降,即随着x的增大y反而减小
1、函数y=-5x的图象过
第 象限, 经过点(0, )
与点(1, ),y随x的增大而 .
二、四
0
-5
减小
课堂练习
2、正比例函数y=(k+1)x的图象中y随x 的增大而增大,则k的取值范围是 。
k>-1
②, ④,⑤
① , ③
理由是:正比例函数 y= kx(k≠0)
⑴当k>0时,函数y随自变量x的增大而增大.
⑵当k<0时,函数y随自变量x的增大而减少 .
4.已知y与x成正比例,且x=2时,y=-6,则当x=9时,求y的值.
解:由题意设函数的解析式:y=kx(k≠0)
所以,-6 = 2k
解得:k = -3
因此,该函数的解析式为:y=-3x
当x=9时,y=-3×9=-27
1、下列函数中,是正比例函数的是( )
A、 B、
C、 D、y=2x2
B
三检测
2、在下列图像中,表示函数y=-kx
(k<0)的图像是( )
A
B
3、正比例函数y=(m-1)x的图象
经过一、三象限,则m的取值
范围是( )
A、m=1 B、m>1
C、m<1 D、m≥1
4、你能任意举出一个过第二、四
象限的正比例函数的解析式吗?
2
6、直线y=(k2+3)x经过 象限,y随x的增大而 。
一、三
增大
7、已知A(-1,y1 ),B(3, y2)都
在直线y=-5x上,则y1与y2的关系
是( )
A、 y1≤y2 B、 y1=y2
C 、y1<y2 D、 y1>y2
D
8、若正比例函数y=(1-2m)x的图像经过点A(x1,y1)和B(x2,y2),当x1<x2时,y1 >y2,则m的取值范围是 。
m>
(1)本节课,我们研究了什么,得到了哪些成果?
(2)正比例函数的图象及性质怎样?
(3)我们是怎样进行研究的?
(4)正比例函数研究过程中,你感受最深的是什么?
1.课堂小结
四 拓展
1.已知某种小汽车的耗油量是每100km耗油15升.所使用的汽油今日涨价到5元/升.
(1)写出汽车行驶途中所耗油费 y(元)与行程 x(km)之间的函数关系式;
(2)在平面直角坐标系内描出大致的函数关系图;
(3)计算娄底到长沙220 km所需油费是多少?
y/元
x/km
1 2 3 4 5 6 7 8
6
5
4
3
2
1
O
解:(1)y=5× x ,
即 .
(2)
列表
(3)当
时,
娄底到长沙220公里所需油费是165元.
描点
连线
2.知识延伸
x 0 4
y 0 3
2.汽车由A城驶往相距120km的B城,s(km)表示
汽车离开A城的距离,t(h)表示汽车行驶的
时间,如图:
⑴求汽车行驶的速度。
⑵当t=1时,
汽车离开A城有多远?
⑶当s=100时,
汽车行驶了多长时间?
t/h
0
s/km
3.比较大小:
(1)k1 k2;(2)k3 k4;
(3)比较k1, k2, k3, k4大小,并用不等号连接.
<
k1<k2 <k3 <k4
<
教科书第98页习题19.2第2题;
用简便方法画下列函数的图象,并说说当x 增
大时,函数值 y 分别怎样变化:
(1)y =4x;(2)y =-2x.
课后作业
