2019年数学同步必修一北师大版:第二章 二次函数性质的再研究 学案
文档属性
| 名称 | 2019年数学同步必修一北师大版:第二章 二次函数性质的再研究 学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 201.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 14:29:55 | ||
图片预览



文档简介
§4 二次函数性质的再研究
学习目标 1.掌握配方法,理解a,b,c(或a,h,k)对二次函数图像的作用.2.理解由y=x2到y=a(x+h)2+k的图像变换方法.3.能根据条件灵活选择二次函数的三种形式求解析式.4.掌握二次函数的性质.
知识点一 二次函数的配方法
思考 y=4x2-4x-1如何配方?你能由此求出方程4x2-4x-1=0的根吗?
答案 y=4(x2-x)-1=4-1
=42-2.
令y=0,即4x2-4x-1=0,
42-2=0,
2=,
x=±=.
梳理 对于一般的二次函数y=ax2+bx+c(a≠0),可类似地配方为y=a2+,由此可得二次函数的值域、顶点等性质,y=x2与y=ax2+bx+c图像间的关系以及二次方程求根公式等.所以配方法是非常重要的数学方法.
知识点二 图像变换
思考 y=x2和y=2(x+1)2+3的图像之间有什么关系?
答案 y=x2的图像各点纵坐标变为原来的2倍,可得y=2x2的图像;再把y=2x2的图像向左平移1个单位长度,再上平移3个单位长度,得y=2(x+1)2+3的图像.
梳理 由y=x2的图像各点纵坐标变为原来的a倍,左移个单位长度,上移个单位长度,可得y=a2+的图像,即y=ax2+bx+c的图像.
知识点三 二次函数的三种形式
思考 我们知道y=x2-2x=(x-1)2-1=(x-2)x,那么点(1,-1),数0,2是y=x2-2x的什么?
答案 点(1,-1)是y=x2-2x的顶点,数0,2是方程x2-2x=0的两根.
梳理 (1)二次函数的一般式y=ax2+bx+c(a≠0).
(2)如果已知二次函数的顶点坐标为(-h,k),则可将二次函数设为y=a(x+h)2+k.
(3)如果已知方程ax2+bx+c=0的两根x1,x2(即抛物线与x轴交点横坐标),可设为y=a(x-x1)(x-x2).
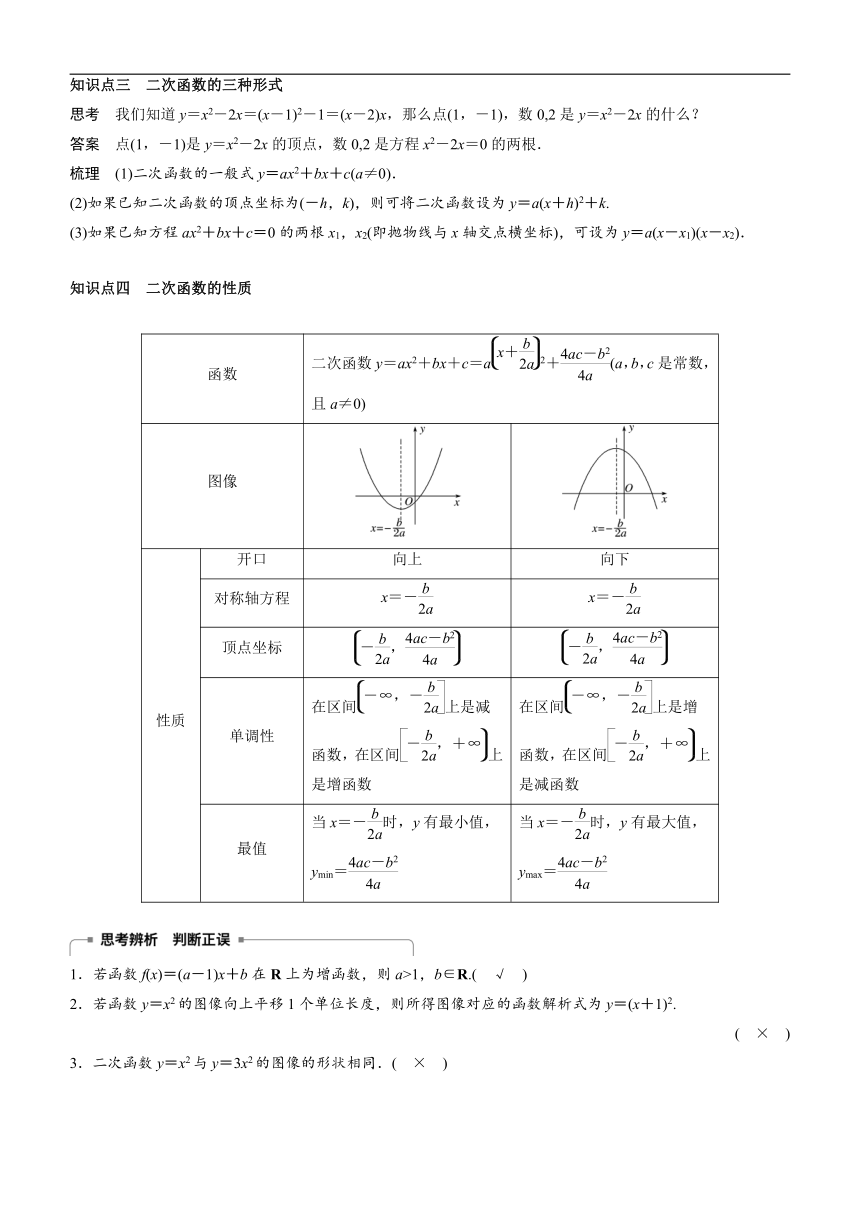
知识点四 二次函数的性质
函数
二次函数y=ax2+bx+c=a2+(a,b,c是常数,且a≠0)
图像
性质
开口
向上
向下
对称轴方程
x=-
x=-
顶点坐标
单调性
在区间上是减函数,在区间上是增函数
在区间上是增函数,在区间上是减函数
最值
当x=-时,y有最小值,ymin=
当x=-时,y有最大值,ymax=
1.若函数f(x)=(a-1)x+b在R上为增函数,则a>1,b∈R.( √ )
2.若函数y=x2的图像向上平移1个单位长度,则所得图像对应的函数解析式为y=(x+1)2.
( × )
3.二次函数y=x2与y=3x2的图像的形状相同.( × )
类型一 二次函数解析式的求解
例1 已知二次函数y=ax2+bx+c(a≠0)的图像与x轴相交于点A(-3,0),对称轴为x=-1,顶点M到x轴的距离为2,求此函数的解析式.
考点 二次函数解析式求法
题点 一般式求法
解 方法一 代入A(-3,0),
有9a-3b+c=0,①
由对称轴为x=-1,得-=-1,②
顶点M到x轴的距离为|a-b+c-0|=2,③
联立①②③解得或
所以此函数的解析式为y=x2+x-或y=-x2-x+.
考点 二次函数解析式求法
题点 顶点式求法
方法二 因为二次函数图像的对称轴是x=-1,
又顶点M到x轴的距离为2,所以顶点的坐标为(-1,2)或(-1,-2),
故可得二次函数的解析式为y=a(x+1)2+2或y=a(x+1)2-2.
因为图像过点A(-3,0),所以0=a(-3+1)2+2或0=a(-3+1)2-2,解得a=-或a=.
故所求二次函数的解析式为y=-(x+1)2+2=-x2-x+或y=(x+1)2-2=x2+x-.
考点 二次函数解析式的求法
题点 两根式求法
方法三 因为二次函数图像的对称轴为x=-1,
又图像过点A(-3,0),所以点A关于对称轴的对称点A′(1,0)也在图像上,
所以可得二次函数的解析式为y=a(x+3)(x-1).
由题意得顶点坐标为(-1,2)或(-1,-2),
分别代入上式,解得a=-或a=.
故所求二次函数的解析式为y=-(x+3)(x-1)=-x2-x+或y=(x+3)(x-1)=x2+x-.
反思与感悟 求二次函数解析式的步骤
跟踪训练1 (1)y=ax2+6x-8与直线y=-3x交于点A(1,m),求a.
考点 二次函数解析式的求法
题点 一般式求法
解 把A(1,m)代入y=-3x,得m=-3,
把(1,-3)代入y=ax2+6x-8,得
a+6-8=-3,即a=-1.
(2)f(x)=x2+bx+c,若f(-4)=f(0),f(-2)=-2,求f(x).
考点 二次函数解析式求法
题点 顶点式求法
解 方法一 由f(-4)=f(0),知f(x)的对称轴为
x==-2,
又f(-2)=-2,∴顶点坐标为(-2,-2),
∴f(x)=(x+2)2-2=x2+4x+2.
考点 二次函数解析式的求法
题点 两根式求法
方法二 由f(-4)=f(0),可设f(x)=x(x+4)+c.
代入x=-2,得-2×(-2+4)+c=-2,∴c=2.
∴f(x)=x2+4x+2.
类型二 二次函数的图像及变换
例2 由函数y=x2的图像如何得到f(x)=-x2+2x+3的图像.
考点 二次函数图像
题点 二次函数图像变换
解 f(x)=-x2+2x+3=-(x2-2x)+3
=-(x2-2x+1-1)+3=-(x-1)2+4,
∴由y=-x2的图象与y=x2的图像关于x轴对称,
可得y=-x2的图像.
由y=-x2的图像向右平移1个单位长度,向上平移4个单位长度,可得y=-(x-1)2+4,即y=-x2+2x+3的图像.
引申探究
利用f(x)=-x2+2x+3的图像比较f(-1),f(2)的大小.
解 f(x)图像如图.
由图知越接近对称轴,函数值越大.
由|-1-1|=2>|2-1|=1,
即f(2)比f(-1)更接近对称轴,∴f(2)>f(-1).
反思与感悟 处理二次函数y=ax2+bx+c(a≠0)的图像问题,主要是考虑其图像特征如开口、顶点、与x轴交点、与y轴交点、对称轴等与系数a,b,c之间的关系.
在图像变换中,记住“h正左移,h负右移,k正上移,k负下移”.
跟踪训练2 将二次函数f(x)=x2+bx+c的图像向左平移2个单位长度,再向上平移3个单位长度,得到二次函数f(x)=x2-2x+1的图像,则b=______,c=______.
考点 二次函数图像
题点 二次函数图像变换
答案 -6 6
解析 f(x)=x2-2x+1=(x-1)2,其图像顶点为(1,0).
将二次函数f(x)=x2-2x+1的图像向下平移3个单位长度,再向右平移2个单位长度后的图像的顶点为(3,-3),得到的抛物线为y=(x-3)2-3,即f(x)=x2+bx+c,
∴(x-3)2-3=x2+bx+c,即x2-6x+6=x2+bx+c,
∴b=-6,c=6.
类型三 二次函数的性质
例3 已知函数f(x)=x2-3x-:
(1)求函数图像的顶点坐标、对称轴方程和最值;
(2)若x∈[1,4],求函数值域.
考点 二次函数性质
题点 由解析式研究二次函数性质
解 (1)对函数右端的表达式配方,得
f(x)=(x-3)2-,
所以函数图像的顶点坐标为,
对称轴方程为x=3,最小值为-,无最大值.
(2)由于3∈[1,4],所以函数在区间[1,3]上是减函数,在区间[3,4]上是增函数,
所以当x=3时,ymin=-,
当x=1时,ymax=×4-=-,
所以函数的值域为.
反思与感悟 解析式、图像、性质三者各有特点又联系紧密,应用时在三者间灵活转化可使问题更易解决.
跟踪训练3 已知函数f(x)=ax2+2ax+1在区间[-1,2]上有最大值4,求实数a的值.
考点 二次函数性质
题点 由性质求参数范围
解 f(x)=a(x+1)2+1-a.
当a=0时,函数f(x)在区间[-1,2]上的值不变,恒为常数1,不符合题意,舍去;
当a>0时,函数f(x)在区间[-1,2]上是增函数,最大值为f(2)=8a+1=4,解得a=;
当a<0时,函数f(x)在区间[-1,2]上是减函数,最大值为f(-1)=1-a=4,解得a=-3.
综上,a的值为-3或.
1.二次函数f(x)=ax2+bx+c(a≠0)与g(x)=bx2+ax+c(b≠0)的图像可能是下图中的( )
考点 二次函数图像
题点 图像与a,b,c的关系
答案 D
解析 由于f(x),g(x)的图像的对称轴方程分别是x=-,x=-,则-与-同号,即f(x),g(x)的图像的对称轴位于y轴的同一侧,由此排除A,B;由C,D中给出的图像,可判定f(x),g(x)的图像的开口方向相反,故ab<0,于是->0,->0,即f(x),g(x)的图像的对称轴都位于y轴右侧,排除C,故选D.
2.设二次函数y=f(x)满足f(4+x)=f(4-x),又f(x)在[4,+∞)上是减函数,且f(a)≥f(0),则实数a的取值范围是( )
A.a≥4
B.0≤a≤8
C.a<0
D.a<0或a≥8
考点 二次函数性质
题点 二次函数性质综合应用
答案 B
解析 由题意知二次函数f(x)的图像关于直线x=4对称,则有f(0)=f(8).因为f(x)在[4,
+∞)上是减函数,所以f(x)在(-∞,4]上是增函数.当a∈(-∞,4]时,由f(a)≥f(0),得0≤a≤4;当a∈[4,+∞)时,由f(a)≥f(0),即f(a)≥f(8),得4≤a≤8.综上可知0≤a≤8.
3.已知f(x)=x2+bx+c,且f(-1)=f(3),则( )
A.f(1)>c>f(-1)
B.f(1)C.c>f(-1)>f(1)
D.c考点 二次函数性质
题点 二次函数的单调性
答案 B
解析 因为f(-1)=f(3),所以f(x)图像的对称轴为x=1,因此函数在区间(-∞,1]上是减函数,又c=f(0),所以f(1)4.根据下列条件,求二次函数y=f(x)的解析式.
(1)图像过点(2,0),(4,0),(0,3);
(2)图像顶点为(1,2)并且过点(0,4);
(3)过点(1,1),(0,2),(3,5).
考点 二次函数解析式求法
题点 (1)两根式求法
(2)顶点式求法
(3)一般式求法
解 (1)由题意可设二次函数解析式为y=a(x-2)(x-4),
将(0,3)代入得a=.
∴所求二次函数解析式为y=(x-2)(x-4).
(2)由题意可设二次函数解析式为y=a(x-1)2+2,
将(0,4)代入得a=2,
∴所求二次函数解析式为y=2(x-1)2+2.
(3)由题意可设二次函数解析式为y=ax2+bx+c,
将(1,1),(0,2),(3,5)代入得
解得
∴所求二次函数解析式为y=x2-2x+2.
1.配方法是重要的数学方法,在处理二次函数图像变换,研究二次函数性质时使用频繁.
2.二次函数图像变换规律可以推广到一般函数,即:
(1)y=f(x)y=f(x+a);
(2)y=f(x)y=f(x)+b;
(3)y=f(x)y=af(x)(a>0);
(4)y=f(x)y=-f(x);
(5)y=f(x)y=f(-x).
2
学习目标 1.掌握配方法,理解a,b,c(或a,h,k)对二次函数图像的作用.2.理解由y=x2到y=a(x+h)2+k的图像变换方法.3.能根据条件灵活选择二次函数的三种形式求解析式.4.掌握二次函数的性质.
知识点一 二次函数的配方法
思考 y=4x2-4x-1如何配方?你能由此求出方程4x2-4x-1=0的根吗?
答案 y=4(x2-x)-1=4-1
=42-2.
令y=0,即4x2-4x-1=0,
42-2=0,
2=,
x=±=.
梳理 对于一般的二次函数y=ax2+bx+c(a≠0),可类似地配方为y=a2+,由此可得二次函数的值域、顶点等性质,y=x2与y=ax2+bx+c图像间的关系以及二次方程求根公式等.所以配方法是非常重要的数学方法.
知识点二 图像变换
思考 y=x2和y=2(x+1)2+3的图像之间有什么关系?
答案 y=x2的图像各点纵坐标变为原来的2倍,可得y=2x2的图像;再把y=2x2的图像向左平移1个单位长度,再上平移3个单位长度,得y=2(x+1)2+3的图像.
梳理 由y=x2的图像各点纵坐标变为原来的a倍,左移个单位长度,上移个单位长度,可得y=a2+的图像,即y=ax2+bx+c的图像.
知识点三 二次函数的三种形式
思考 我们知道y=x2-2x=(x-1)2-1=(x-2)x,那么点(1,-1),数0,2是y=x2-2x的什么?
答案 点(1,-1)是y=x2-2x的顶点,数0,2是方程x2-2x=0的两根.
梳理 (1)二次函数的一般式y=ax2+bx+c(a≠0).
(2)如果已知二次函数的顶点坐标为(-h,k),则可将二次函数设为y=a(x+h)2+k.
(3)如果已知方程ax2+bx+c=0的两根x1,x2(即抛物线与x轴交点横坐标),可设为y=a(x-x1)(x-x2).
知识点四 二次函数的性质
函数
二次函数y=ax2+bx+c=a2+(a,b,c是常数,且a≠0)
图像
性质
开口
向上
向下
对称轴方程
x=-
x=-
顶点坐标
单调性
在区间上是减函数,在区间上是增函数
在区间上是增函数,在区间上是减函数
最值
当x=-时,y有最小值,ymin=
当x=-时,y有最大值,ymax=
1.若函数f(x)=(a-1)x+b在R上为增函数,则a>1,b∈R.( √ )
2.若函数y=x2的图像向上平移1个单位长度,则所得图像对应的函数解析式为y=(x+1)2.
( × )
3.二次函数y=x2与y=3x2的图像的形状相同.( × )
类型一 二次函数解析式的求解
例1 已知二次函数y=ax2+bx+c(a≠0)的图像与x轴相交于点A(-3,0),对称轴为x=-1,顶点M到x轴的距离为2,求此函数的解析式.
考点 二次函数解析式求法
题点 一般式求法
解 方法一 代入A(-3,0),
有9a-3b+c=0,①
由对称轴为x=-1,得-=-1,②
顶点M到x轴的距离为|a-b+c-0|=2,③
联立①②③解得或
所以此函数的解析式为y=x2+x-或y=-x2-x+.
考点 二次函数解析式求法
题点 顶点式求法
方法二 因为二次函数图像的对称轴是x=-1,
又顶点M到x轴的距离为2,所以顶点的坐标为(-1,2)或(-1,-2),
故可得二次函数的解析式为y=a(x+1)2+2或y=a(x+1)2-2.
因为图像过点A(-3,0),所以0=a(-3+1)2+2或0=a(-3+1)2-2,解得a=-或a=.
故所求二次函数的解析式为y=-(x+1)2+2=-x2-x+或y=(x+1)2-2=x2+x-.
考点 二次函数解析式的求法
题点 两根式求法
方法三 因为二次函数图像的对称轴为x=-1,
又图像过点A(-3,0),所以点A关于对称轴的对称点A′(1,0)也在图像上,
所以可得二次函数的解析式为y=a(x+3)(x-1).
由题意得顶点坐标为(-1,2)或(-1,-2),
分别代入上式,解得a=-或a=.
故所求二次函数的解析式为y=-(x+3)(x-1)=-x2-x+或y=(x+3)(x-1)=x2+x-.
反思与感悟 求二次函数解析式的步骤
跟踪训练1 (1)y=ax2+6x-8与直线y=-3x交于点A(1,m),求a.
考点 二次函数解析式的求法
题点 一般式求法
解 把A(1,m)代入y=-3x,得m=-3,
把(1,-3)代入y=ax2+6x-8,得
a+6-8=-3,即a=-1.
(2)f(x)=x2+bx+c,若f(-4)=f(0),f(-2)=-2,求f(x).
考点 二次函数解析式求法
题点 顶点式求法
解 方法一 由f(-4)=f(0),知f(x)的对称轴为
x==-2,
又f(-2)=-2,∴顶点坐标为(-2,-2),
∴f(x)=(x+2)2-2=x2+4x+2.
考点 二次函数解析式的求法
题点 两根式求法
方法二 由f(-4)=f(0),可设f(x)=x(x+4)+c.
代入x=-2,得-2×(-2+4)+c=-2,∴c=2.
∴f(x)=x2+4x+2.
类型二 二次函数的图像及变换
例2 由函数y=x2的图像如何得到f(x)=-x2+2x+3的图像.
考点 二次函数图像
题点 二次函数图像变换
解 f(x)=-x2+2x+3=-(x2-2x)+3
=-(x2-2x+1-1)+3=-(x-1)2+4,
∴由y=-x2的图象与y=x2的图像关于x轴对称,
可得y=-x2的图像.
由y=-x2的图像向右平移1个单位长度,向上平移4个单位长度,可得y=-(x-1)2+4,即y=-x2+2x+3的图像.
引申探究
利用f(x)=-x2+2x+3的图像比较f(-1),f(2)的大小.
解 f(x)图像如图.
由图知越接近对称轴,函数值越大.
由|-1-1|=2>|2-1|=1,
即f(2)比f(-1)更接近对称轴,∴f(2)>f(-1).
反思与感悟 处理二次函数y=ax2+bx+c(a≠0)的图像问题,主要是考虑其图像特征如开口、顶点、与x轴交点、与y轴交点、对称轴等与系数a,b,c之间的关系.
在图像变换中,记住“h正左移,h负右移,k正上移,k负下移”.
跟踪训练2 将二次函数f(x)=x2+bx+c的图像向左平移2个单位长度,再向上平移3个单位长度,得到二次函数f(x)=x2-2x+1的图像,则b=______,c=______.
考点 二次函数图像
题点 二次函数图像变换
答案 -6 6
解析 f(x)=x2-2x+1=(x-1)2,其图像顶点为(1,0).
将二次函数f(x)=x2-2x+1的图像向下平移3个单位长度,再向右平移2个单位长度后的图像的顶点为(3,-3),得到的抛物线为y=(x-3)2-3,即f(x)=x2+bx+c,
∴(x-3)2-3=x2+bx+c,即x2-6x+6=x2+bx+c,
∴b=-6,c=6.
类型三 二次函数的性质
例3 已知函数f(x)=x2-3x-:
(1)求函数图像的顶点坐标、对称轴方程和最值;
(2)若x∈[1,4],求函数值域.
考点 二次函数性质
题点 由解析式研究二次函数性质
解 (1)对函数右端的表达式配方,得
f(x)=(x-3)2-,
所以函数图像的顶点坐标为,
对称轴方程为x=3,最小值为-,无最大值.
(2)由于3∈[1,4],所以函数在区间[1,3]上是减函数,在区间[3,4]上是增函数,
所以当x=3时,ymin=-,
当x=1时,ymax=×4-=-,
所以函数的值域为.
反思与感悟 解析式、图像、性质三者各有特点又联系紧密,应用时在三者间灵活转化可使问题更易解决.
跟踪训练3 已知函数f(x)=ax2+2ax+1在区间[-1,2]上有最大值4,求实数a的值.
考点 二次函数性质
题点 由性质求参数范围
解 f(x)=a(x+1)2+1-a.
当a=0时,函数f(x)在区间[-1,2]上的值不变,恒为常数1,不符合题意,舍去;
当a>0时,函数f(x)在区间[-1,2]上是增函数,最大值为f(2)=8a+1=4,解得a=;
当a<0时,函数f(x)在区间[-1,2]上是减函数,最大值为f(-1)=1-a=4,解得a=-3.
综上,a的值为-3或.
1.二次函数f(x)=ax2+bx+c(a≠0)与g(x)=bx2+ax+c(b≠0)的图像可能是下图中的( )
考点 二次函数图像
题点 图像与a,b,c的关系
答案 D
解析 由于f(x),g(x)的图像的对称轴方程分别是x=-,x=-,则-与-同号,即f(x),g(x)的图像的对称轴位于y轴的同一侧,由此排除A,B;由C,D中给出的图像,可判定f(x),g(x)的图像的开口方向相反,故ab<0,于是->0,->0,即f(x),g(x)的图像的对称轴都位于y轴右侧,排除C,故选D.
2.设二次函数y=f(x)满足f(4+x)=f(4-x),又f(x)在[4,+∞)上是减函数,且f(a)≥f(0),则实数a的取值范围是( )
A.a≥4
B.0≤a≤8
C.a<0
D.a<0或a≥8
考点 二次函数性质
题点 二次函数性质综合应用
答案 B
解析 由题意知二次函数f(x)的图像关于直线x=4对称,则有f(0)=f(8).因为f(x)在[4,
+∞)上是减函数,所以f(x)在(-∞,4]上是增函数.当a∈(-∞,4]时,由f(a)≥f(0),得0≤a≤4;当a∈[4,+∞)时,由f(a)≥f(0),即f(a)≥f(8),得4≤a≤8.综上可知0≤a≤8.
3.已知f(x)=x2+bx+c,且f(-1)=f(3),则( )
A.f(1)>c>f(-1)
B.f(1)
D.c
题点 二次函数的单调性
答案 B
解析 因为f(-1)=f(3),所以f(x)图像的对称轴为x=1,因此函数在区间(-∞,1]上是减函数,又c=f(0),所以f(1)
(1)图像过点(2,0),(4,0),(0,3);
(2)图像顶点为(1,2)并且过点(0,4);
(3)过点(1,1),(0,2),(3,5).
考点 二次函数解析式求法
题点 (1)两根式求法
(2)顶点式求法
(3)一般式求法
解 (1)由题意可设二次函数解析式为y=a(x-2)(x-4),
将(0,3)代入得a=.
∴所求二次函数解析式为y=(x-2)(x-4).
(2)由题意可设二次函数解析式为y=a(x-1)2+2,
将(0,4)代入得a=2,
∴所求二次函数解析式为y=2(x-1)2+2.
(3)由题意可设二次函数解析式为y=ax2+bx+c,
将(1,1),(0,2),(3,5)代入得
解得
∴所求二次函数解析式为y=x2-2x+2.
1.配方法是重要的数学方法,在处理二次函数图像变换,研究二次函数性质时使用频繁.
2.二次函数图像变换规律可以推广到一般函数,即:
(1)y=f(x)y=f(x+a);
(2)y=f(x)y=f(x)+b;
(3)y=f(x)y=af(x)(a>0);
(4)y=f(x)y=-f(x);
(5)y=f(x)y=f(-x).
2
