2019年数学同步必修一北师大版:第二章 简单的幂函数(二) 学案
文档属性
| 名称 | 2019年数学同步必修一北师大版:第二章 简单的幂函数(二) 学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 235.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 00:00:00 | ||
图片预览



文档简介
§5 简单的幂函数(二)
学习目标 1.理解函数奇偶性的定义.2.掌握函数奇偶性的判断和证明方法.3.会应用奇、偶函数图像的对称性解决简单问题.
知识点一 函数奇偶性的几何特征
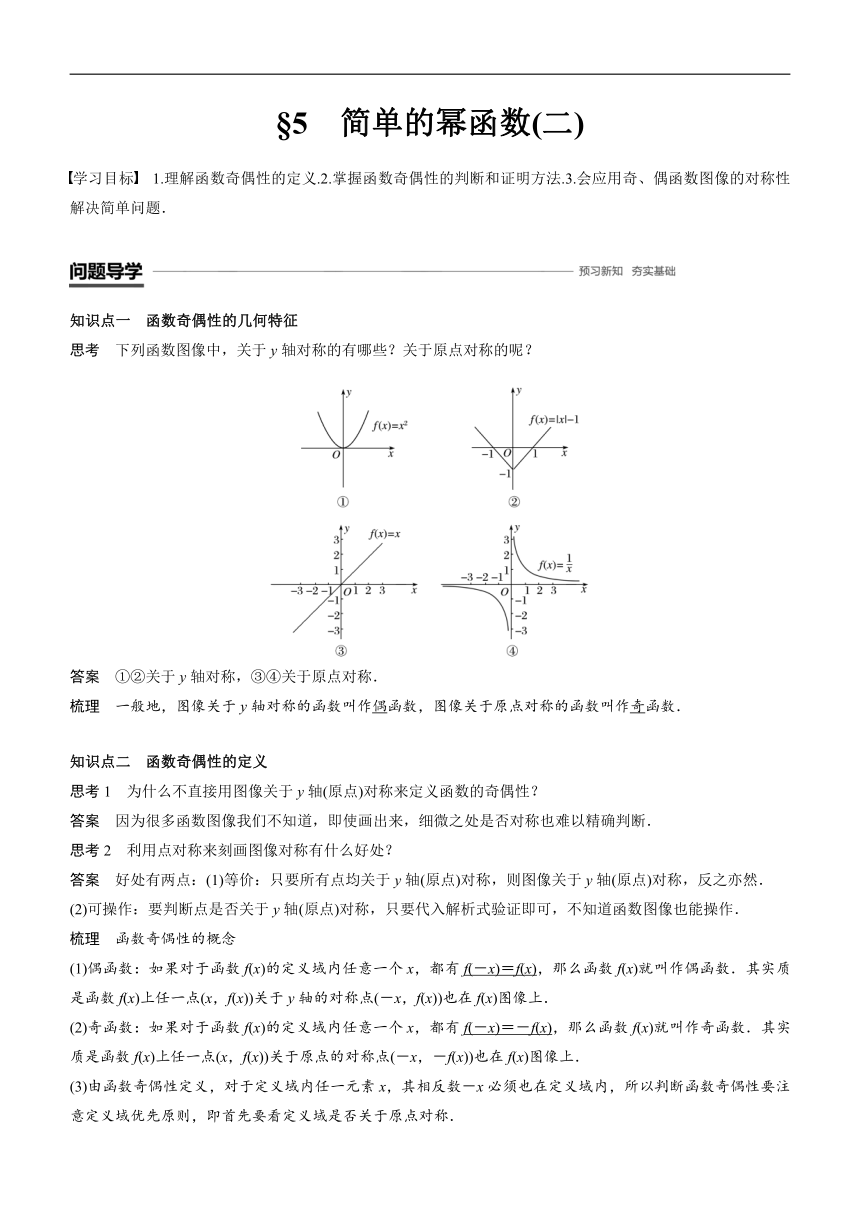
思考 下列函数图像中,关于y轴对称的有哪些?关于原点对称的呢?
答案 ①②关于y轴对称,③④关于原点对称.
梳理 一般地,图像关于y轴对称的函数叫作偶函数,图像关于原点对称的函数叫作奇函数.
知识点二 函数奇偶性的定义
思考1 为什么不直接用图像关于y轴(原点)对称来定义函数的奇偶性?
答案 因为很多函数图像我们不知道,即使画出来,细微之处是否对称也难以精确判断.
思考2 利用点对称来刻画图像对称有什么好处?
答案 好处有两点:(1)等价:只要所有点均关于y轴(原点)对称,则图像关于y轴(原点)对称,反之亦然.
(2)可操作:要判断点是否关于y轴(原点)对称,只要代入解析式验证即可,不知道函数图像也能操作.
梳理 函数奇偶性的概念
(1)偶函数:如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)就叫作偶函数.其实质是函数f(x)上任一点(x,f(x))关于y轴的对称点(-x,f(x))也在f(x)图像上.
(2)奇函数:如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫作奇函数.其实质是函数f(x)上任一点(x,f(x))关于原点的对称点(-x,-f(x))也在f(x)图像上.
(3)由函数奇偶性定义,对于定义域内任一元素x,其相反数-x必须也在定义域内,所以判断函数奇偶性要注意定义域优先原则,即首先要看定义域是否关于原点对称.
知识点三 奇偶性与单调性
思考 观察偶函数y=x2与奇函数y=在(-∞,0)和(0,+∞)上的单调性,你有何猜想?
答案 偶函数y=x2在(-∞,0)和(0,+∞)上的单调性相反;奇函数y=在(-∞,0)和(0,+∞)上的单调性相同.
梳理 (1)若奇函数f(x)在[a,b]上是增函数,且有最大值M,则f(x)在[-b,-a]上是增函数,且有最小值-M.
(2)若偶函数f(x)在(-∞,0)上是减函数,则f(x)在(0,+∞)上是增函数.
(3)知道了函数的奇偶性,我们可以先研究函数的一半,再利用对称性了解其另一半,从而减少工作量.
1.关于y轴对称的图形都是偶函数的图像.( × )
2.若f(x)是奇函数,f(1)=2,则f(-1)=-2.( √ )
3.存在既是奇函数又是偶函数的函数,且不止一个.( √ )
4.有些函数既非奇函数,又非偶函数.( √ )
类型一 判断函数的奇偶性
例1 判断并证明下列函数的奇偶性:
(1)f(x)=;
(2)f(x)=(x+1)(x-1);
(3)f(x)=+.
考点 函数奇偶性的判定与证明
题点 判断简单函数的奇偶性
证明 (1)因为函数的定义域为{x|x∈R且x≠1},∴对于定义域内的-1,其相反数1不在定义域内,故f(x)=既非奇函数又非偶函数.
(2)函数的定义域为R,因为函数f(x)=(x+1)(x-1)=x2-1,又f(-x)=(-x)2-1=x2-1=f(x),所以函数为偶函数.
(3)函数的定义域为{-1,1},因为对定义域内的每一个x,都有f(x)=0,所以f(-x)=f(x),故函数f(x)=+为偶函数.又f(-x)=-f(x),故函数f(x)=+为奇函数.即该函数既是奇函数又是偶函数.
反思与感悟 利用定义法判断函数是否具有奇偶性时,首先应看函数定义域是否关于原点对称,即对于定义域内的任意一个x,则-x也一定属于定义域.
跟踪训练1 判断并证明下列函数的奇偶性:
(1)f(x)=(x-2);
(2)f(x)=x|x|;
(3)f(x),g(x)是定义在R上的奇函数,试判断y=f(x)+g(x),y=f(x)g(x),y=f[g(x)]的奇偶性.
考点 函数奇偶性的判定与证明
题点 判断函数的奇偶性
解 (1)由≥0,得定义域为[-2,2),关于原点不对称,故f(x)为非奇非偶函数.
(2)函数的定义域为R,因为f(-x)=(-x)|-x|=-x|x|=-f(x),所以函数为奇函数.
(3)∵f(x),g(x)是定义在R上的奇函数,
∴f(-x)+g(-x)=-f(x)-g(x)=-[f(x)+g(x)],y=f(x)+g(x)是奇函数.
f(-x)g(-x)=[-f(x)][-g(x)]=f(x)g(x),y=f(x)g(x)是偶函数.
f[g(-x)]=f[-g(x)]=-f[g(x)],y=f[g(x)]是奇函数.
类型二 奇偶性的应用
命题角度1 奇偶函数图像的对称性的应用
例2 定义在R上的奇函数f(x)在[0,+∞)上的图像如图所示.
(1)画出f(x)的图像;
(2)解不等式xf(x)>0.
考点 函数图像的对称性
题点 中心对称问题
解 (1)先描出(1,1),(2,0)关于原点的对称点(-1,-1),(-2,0),连线可得f(x)的图像如图.
(2)xf(x)>0即图像上横坐标、纵坐标同号.结合图像可知,xf(x)>0的解集是(-2,0)∪(0,2).
引申探究
把例2中的“奇函数”改为“偶函数”,重做该题.
解 (1)f(x)的图像如图所示:
(2)xf(x)>0的解集是(-∞,-2)∪(0,2).
反思与感悟 鉴于奇(偶)函数图像关于原点(y轴)对称,可以用这一特性去画图,求值,求解析式,研究单调性.
跟踪训练2 已知奇函数f(x)的定义域为[-5,5],且在区间[0,5]上的图像如图所示.
(1)画出在区间[-5,0]上的图像;
(2)写出使f(x)<0的x的取值集合.
考点 函数图像的对称性
题点 中心对称问题
解 (1)如图,在[0,5]上的图像上选取5个关键点O,A,B,C,D.
分别描出它们关于原点的对称点O′,A′,B′,C′,D′,
再用光滑曲线连接即得.
(2)由(1)图可知,当且仅当x∈(-2,0)∪(2,5)时,f(x)<0.
∴使f(x)<0的x的取值集合为(-2,0)∪(2,5).
命题角度2 应用函数奇偶性求解析式
例3 函数f(x)是定义域为R的奇函数,当x>0时,f(x)=-x+1,求当x<0时,f(x)的解析式.
考点 函数奇偶性的应用
题点 利用奇偶性求函数的解析式
解 设x<0,则-x>0,
∴f(-x)=-(-x)+1=x+1,
又∵函数f(x)是定义域为R的奇函数,
∴f(-x)=-f(x)=x+1,
∴当x<0时,f(x)=-x-1.
反思与感悟 利用函数的奇偶性求函数解析式
已知函数f(x)在区间[a,b]上的解析式,求函数f(x)在区间[-b,-a]上的解析式的一般方法:
(1)设:设-b≤x≤-a,则a≤-x≤b.
(2)求f(-x):根据已知条件f(x)在区间[a,b]上的解析式可求得f(-x)的解析式.
(3)求f(x):根据函数f(x)的奇偶性来实现函数的解析式在f(x)与f(-x)之间的相互转化.
跟踪训练3 已知y=f(x)是定义在R上的奇函数,且当x>0时,f(x)=2x-x2.求y=f(x)的解析式.
考点 函数奇偶性的应用
题点 利用奇偶性求函数的解析式
解 设x<0,则-x>0,因为f(x)是奇函数,
所以f(x)=-f(-x)=-[2(-x)-(-x)2]=2x+x2.
因为y=f(x)是R上的奇函数,所以f(0)=0.
所以f(x)=
命题角度3 奇偶性对单调性的影响
例4 设f(x)是偶函数,在区间[a,b]上是减函数,试证f(x)在区间[-b,-a]上是增函数.
考点 单调性与奇偶性的综合应用
题点 判断或证明奇偶函数在某区间上的单调性
证明 设x1,x2是区间[-b,-a]上任意两个值,
且有x1∵-b≤x1∴a≤-x2<-x1≤b.
∵f(x)在[a,b]上是减函数,
∴f(-x2)>f(-x1).
∵f(x)为偶函数,即f(-x)=f(x),
∴f(-x2)=f(x2),f(-x1)=f(x1).
∴f(x2)>f(x1),即f(x1)∴函数f(x)在区间[-b,-a]上是增函数.
反思与感悟 与求解析式一样,证哪个区间上的单调性,设x1,x2属于哪个区间.同样,求哪个区间上的最值,也设x属于哪个区间.
跟踪训练4 已知偶函数f(x)在[0,+∞)上单调递减,f(2)=0.若f(x-1)>0,则x的取值范围是________.
考点 单调性与奇偶性的综合应用
题点 利用奇偶性、单调性解不等式
答案 (-1,3)
解析 ∵f(x)为偶函数,
∴f(x-1)=f(|x-1|),
又f(2)=0,∴f(x-1)>0,即f(|x-1|)>f(2),
∵|x-1|,2∈[0,+∞),
且f(x)在[0,+∞)上单调递减.
∴|x-1|<2,即-2∴x的取值范围为(-1,3).
1.下列函数为偶函数的是( )
A.f(x)=x-1
B.f(x)=x2+x
C.f(x)=2x-2-x
D.f(x)=2x+2-x
考点 函数的奇偶性概念
题点 判断函数的奇偶性
答案 D
解析 D中,f(-x)=2-x+2x=f(x),
∴f(x)为偶函数.
2.函数f(x)=x(-1A.奇函数
B.偶函数
C.非奇非偶函数
D.既是奇函数又是偶函数
考点 函数奇偶性的判定与证明
题点 判断函数的奇偶性
答案 C
3.已知函数y=f(x)+x是偶函数,且f(2)=1,则f(-2)等于( )
A.-1
B.1
C.-5
D.5
考点 函数图像的对称性
题点 轴对称问题
答案 D
解析 函数y=f(x)+x是偶函数,∴x=±2时函数值相等.
∴f(-2)-2=f(2)+2,∴f(-2)=5,故选D.
4.已知f(x)是奇函数,且当x>0时,f(x)=x-1,则当x<0时f(x)等于( )
A.x+1
B.x-1
C.-x-1
D.-x+1
考点 函数奇偶性的应用
题点 利用奇偶性求函数的解析式
答案 A
5.定义在R上的偶函数f(x)在[0,+∞)上是增函数,若f(a)A.aB.a>b
C.|a|<|b|
D.0≤ab≥0
考点 单调性与奇偶性的综合应用
题点 利用奇偶性、单调性解不等式
答案 C
1.两个定义:对于f(x)定义域内的任意一个x,如果都有f(-x)=-f(x) f(-x)+f(x)=0 f(x)为奇函数;如果都有f(-x)=f(x) f(-x)-f(x)=0 f(x)为偶函数.
2.两个性质:函数为奇函数 它的图像关于原点对称;函数为偶函数 它的图像关于y轴对称.
3.证明一个函数是奇函数,必须对f(x)的定义域内任意一个x,都有f(-x)=-f(x).而证明一个函数不是奇函数,只要能举出一个反例就可以了.
4.(1)根据奇函数的定义,如果一个奇函数在原点处有定义,即f(0)有意义,那么一定有f(0)=0.有时可以用这个结论来否定一个函数为奇函数.
(2)偶函数的一个重要性质:f(|x|)=f(x),它能使自变量化归到[0,+∞)上,避免分类讨论.
5.具有奇偶性的函数的单调性的特点:
(1)奇函数在[a,b]和[-b,-a]上具有相同的单调性.
(2)偶函数在[a,b]和[-b,-a]上具有相反的单调性.
2
学习目标 1.理解函数奇偶性的定义.2.掌握函数奇偶性的判断和证明方法.3.会应用奇、偶函数图像的对称性解决简单问题.
知识点一 函数奇偶性的几何特征
思考 下列函数图像中,关于y轴对称的有哪些?关于原点对称的呢?
答案 ①②关于y轴对称,③④关于原点对称.
梳理 一般地,图像关于y轴对称的函数叫作偶函数,图像关于原点对称的函数叫作奇函数.
知识点二 函数奇偶性的定义
思考1 为什么不直接用图像关于y轴(原点)对称来定义函数的奇偶性?
答案 因为很多函数图像我们不知道,即使画出来,细微之处是否对称也难以精确判断.
思考2 利用点对称来刻画图像对称有什么好处?
答案 好处有两点:(1)等价:只要所有点均关于y轴(原点)对称,则图像关于y轴(原点)对称,反之亦然.
(2)可操作:要判断点是否关于y轴(原点)对称,只要代入解析式验证即可,不知道函数图像也能操作.
梳理 函数奇偶性的概念
(1)偶函数:如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)就叫作偶函数.其实质是函数f(x)上任一点(x,f(x))关于y轴的对称点(-x,f(x))也在f(x)图像上.
(2)奇函数:如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫作奇函数.其实质是函数f(x)上任一点(x,f(x))关于原点的对称点(-x,-f(x))也在f(x)图像上.
(3)由函数奇偶性定义,对于定义域内任一元素x,其相反数-x必须也在定义域内,所以判断函数奇偶性要注意定义域优先原则,即首先要看定义域是否关于原点对称.
知识点三 奇偶性与单调性
思考 观察偶函数y=x2与奇函数y=在(-∞,0)和(0,+∞)上的单调性,你有何猜想?
答案 偶函数y=x2在(-∞,0)和(0,+∞)上的单调性相反;奇函数y=在(-∞,0)和(0,+∞)上的单调性相同.
梳理 (1)若奇函数f(x)在[a,b]上是增函数,且有最大值M,则f(x)在[-b,-a]上是增函数,且有最小值-M.
(2)若偶函数f(x)在(-∞,0)上是减函数,则f(x)在(0,+∞)上是增函数.
(3)知道了函数的奇偶性,我们可以先研究函数的一半,再利用对称性了解其另一半,从而减少工作量.
1.关于y轴对称的图形都是偶函数的图像.( × )
2.若f(x)是奇函数,f(1)=2,则f(-1)=-2.( √ )
3.存在既是奇函数又是偶函数的函数,且不止一个.( √ )
4.有些函数既非奇函数,又非偶函数.( √ )
类型一 判断函数的奇偶性
例1 判断并证明下列函数的奇偶性:
(1)f(x)=;
(2)f(x)=(x+1)(x-1);
(3)f(x)=+.
考点 函数奇偶性的判定与证明
题点 判断简单函数的奇偶性
证明 (1)因为函数的定义域为{x|x∈R且x≠1},∴对于定义域内的-1,其相反数1不在定义域内,故f(x)=既非奇函数又非偶函数.
(2)函数的定义域为R,因为函数f(x)=(x+1)(x-1)=x2-1,又f(-x)=(-x)2-1=x2-1=f(x),所以函数为偶函数.
(3)函数的定义域为{-1,1},因为对定义域内的每一个x,都有f(x)=0,所以f(-x)=f(x),故函数f(x)=+为偶函数.又f(-x)=-f(x),故函数f(x)=+为奇函数.即该函数既是奇函数又是偶函数.
反思与感悟 利用定义法判断函数是否具有奇偶性时,首先应看函数定义域是否关于原点对称,即对于定义域内的任意一个x,则-x也一定属于定义域.
跟踪训练1 判断并证明下列函数的奇偶性:
(1)f(x)=(x-2);
(2)f(x)=x|x|;
(3)f(x),g(x)是定义在R上的奇函数,试判断y=f(x)+g(x),y=f(x)g(x),y=f[g(x)]的奇偶性.
考点 函数奇偶性的判定与证明
题点 判断函数的奇偶性
解 (1)由≥0,得定义域为[-2,2),关于原点不对称,故f(x)为非奇非偶函数.
(2)函数的定义域为R,因为f(-x)=(-x)|-x|=-x|x|=-f(x),所以函数为奇函数.
(3)∵f(x),g(x)是定义在R上的奇函数,
∴f(-x)+g(-x)=-f(x)-g(x)=-[f(x)+g(x)],y=f(x)+g(x)是奇函数.
f(-x)g(-x)=[-f(x)][-g(x)]=f(x)g(x),y=f(x)g(x)是偶函数.
f[g(-x)]=f[-g(x)]=-f[g(x)],y=f[g(x)]是奇函数.
类型二 奇偶性的应用
命题角度1 奇偶函数图像的对称性的应用
例2 定义在R上的奇函数f(x)在[0,+∞)上的图像如图所示.
(1)画出f(x)的图像;
(2)解不等式xf(x)>0.
考点 函数图像的对称性
题点 中心对称问题
解 (1)先描出(1,1),(2,0)关于原点的对称点(-1,-1),(-2,0),连线可得f(x)的图像如图.
(2)xf(x)>0即图像上横坐标、纵坐标同号.结合图像可知,xf(x)>0的解集是(-2,0)∪(0,2).
引申探究
把例2中的“奇函数”改为“偶函数”,重做该题.
解 (1)f(x)的图像如图所示:
(2)xf(x)>0的解集是(-∞,-2)∪(0,2).
反思与感悟 鉴于奇(偶)函数图像关于原点(y轴)对称,可以用这一特性去画图,求值,求解析式,研究单调性.
跟踪训练2 已知奇函数f(x)的定义域为[-5,5],且在区间[0,5]上的图像如图所示.
(1)画出在区间[-5,0]上的图像;
(2)写出使f(x)<0的x的取值集合.
考点 函数图像的对称性
题点 中心对称问题
解 (1)如图,在[0,5]上的图像上选取5个关键点O,A,B,C,D.
分别描出它们关于原点的对称点O′,A′,B′,C′,D′,
再用光滑曲线连接即得.
(2)由(1)图可知,当且仅当x∈(-2,0)∪(2,5)时,f(x)<0.
∴使f(x)<0的x的取值集合为(-2,0)∪(2,5).
命题角度2 应用函数奇偶性求解析式
例3 函数f(x)是定义域为R的奇函数,当x>0时,f(x)=-x+1,求当x<0时,f(x)的解析式.
考点 函数奇偶性的应用
题点 利用奇偶性求函数的解析式
解 设x<0,则-x>0,
∴f(-x)=-(-x)+1=x+1,
又∵函数f(x)是定义域为R的奇函数,
∴f(-x)=-f(x)=x+1,
∴当x<0时,f(x)=-x-1.
反思与感悟 利用函数的奇偶性求函数解析式
已知函数f(x)在区间[a,b]上的解析式,求函数f(x)在区间[-b,-a]上的解析式的一般方法:
(1)设:设-b≤x≤-a,则a≤-x≤b.
(2)求f(-x):根据已知条件f(x)在区间[a,b]上的解析式可求得f(-x)的解析式.
(3)求f(x):根据函数f(x)的奇偶性来实现函数的解析式在f(x)与f(-x)之间的相互转化.
跟踪训练3 已知y=f(x)是定义在R上的奇函数,且当x>0时,f(x)=2x-x2.求y=f(x)的解析式.
考点 函数奇偶性的应用
题点 利用奇偶性求函数的解析式
解 设x<0,则-x>0,因为f(x)是奇函数,
所以f(x)=-f(-x)=-[2(-x)-(-x)2]=2x+x2.
因为y=f(x)是R上的奇函数,所以f(0)=0.
所以f(x)=
命题角度3 奇偶性对单调性的影响
例4 设f(x)是偶函数,在区间[a,b]上是减函数,试证f(x)在区间[-b,-a]上是增函数.
考点 单调性与奇偶性的综合应用
题点 判断或证明奇偶函数在某区间上的单调性
证明 设x1,x2是区间[-b,-a]上任意两个值,
且有x1
∵f(x)在[a,b]上是减函数,
∴f(-x2)>f(-x1).
∵f(x)为偶函数,即f(-x)=f(x),
∴f(-x2)=f(x2),f(-x1)=f(x1).
∴f(x2)>f(x1),即f(x1)
反思与感悟 与求解析式一样,证哪个区间上的单调性,设x1,x2属于哪个区间.同样,求哪个区间上的最值,也设x属于哪个区间.
跟踪训练4 已知偶函数f(x)在[0,+∞)上单调递减,f(2)=0.若f(x-1)>0,则x的取值范围是________.
考点 单调性与奇偶性的综合应用
题点 利用奇偶性、单调性解不等式
答案 (-1,3)
解析 ∵f(x)为偶函数,
∴f(x-1)=f(|x-1|),
又f(2)=0,∴f(x-1)>0,即f(|x-1|)>f(2),
∵|x-1|,2∈[0,+∞),
且f(x)在[0,+∞)上单调递减.
∴|x-1|<2,即-2
1.下列函数为偶函数的是( )
A.f(x)=x-1
B.f(x)=x2+x
C.f(x)=2x-2-x
D.f(x)=2x+2-x
考点 函数的奇偶性概念
题点 判断函数的奇偶性
答案 D
解析 D中,f(-x)=2-x+2x=f(x),
∴f(x)为偶函数.
2.函数f(x)=x(-1
B.偶函数
C.非奇非偶函数
D.既是奇函数又是偶函数
考点 函数奇偶性的判定与证明
题点 判断函数的奇偶性
答案 C
3.已知函数y=f(x)+x是偶函数,且f(2)=1,则f(-2)等于( )
A.-1
B.1
C.-5
D.5
考点 函数图像的对称性
题点 轴对称问题
答案 D
解析 函数y=f(x)+x是偶函数,∴x=±2时函数值相等.
∴f(-2)-2=f(2)+2,∴f(-2)=5,故选D.
4.已知f(x)是奇函数,且当x>0时,f(x)=x-1,则当x<0时f(x)等于( )
A.x+1
B.x-1
C.-x-1
D.-x+1
考点 函数奇偶性的应用
题点 利用奇偶性求函数的解析式
答案 A
5.定义在R上的偶函数f(x)在[0,+∞)上是增函数,若f(a)
C.|a|<|b|
D.0≤a
考点 单调性与奇偶性的综合应用
题点 利用奇偶性、单调性解不等式
答案 C
1.两个定义:对于f(x)定义域内的任意一个x,如果都有f(-x)=-f(x) f(-x)+f(x)=0 f(x)为奇函数;如果都有f(-x)=f(x) f(-x)-f(x)=0 f(x)为偶函数.
2.两个性质:函数为奇函数 它的图像关于原点对称;函数为偶函数 它的图像关于y轴对称.
3.证明一个函数是奇函数,必须对f(x)的定义域内任意一个x,都有f(-x)=-f(x).而证明一个函数不是奇函数,只要能举出一个反例就可以了.
4.(1)根据奇函数的定义,如果一个奇函数在原点处有定义,即f(0)有意义,那么一定有f(0)=0.有时可以用这个结论来否定一个函数为奇函数.
(2)偶函数的一个重要性质:f(|x|)=f(x),它能使自变量化归到[0,+∞)上,避免分类讨论.
5.具有奇偶性的函数的单调性的特点:
(1)奇函数在[a,b]和[-b,-a]上具有相同的单调性.
(2)偶函数在[a,b]和[-b,-a]上具有相反的单调性.
2
