2019年数学同步必修一北师大版:第二章 简单的幂函数(一) 学案
文档属性
| 名称 | 2019年数学同步必修一北师大版:第二章 简单的幂函数(一) 学案 | 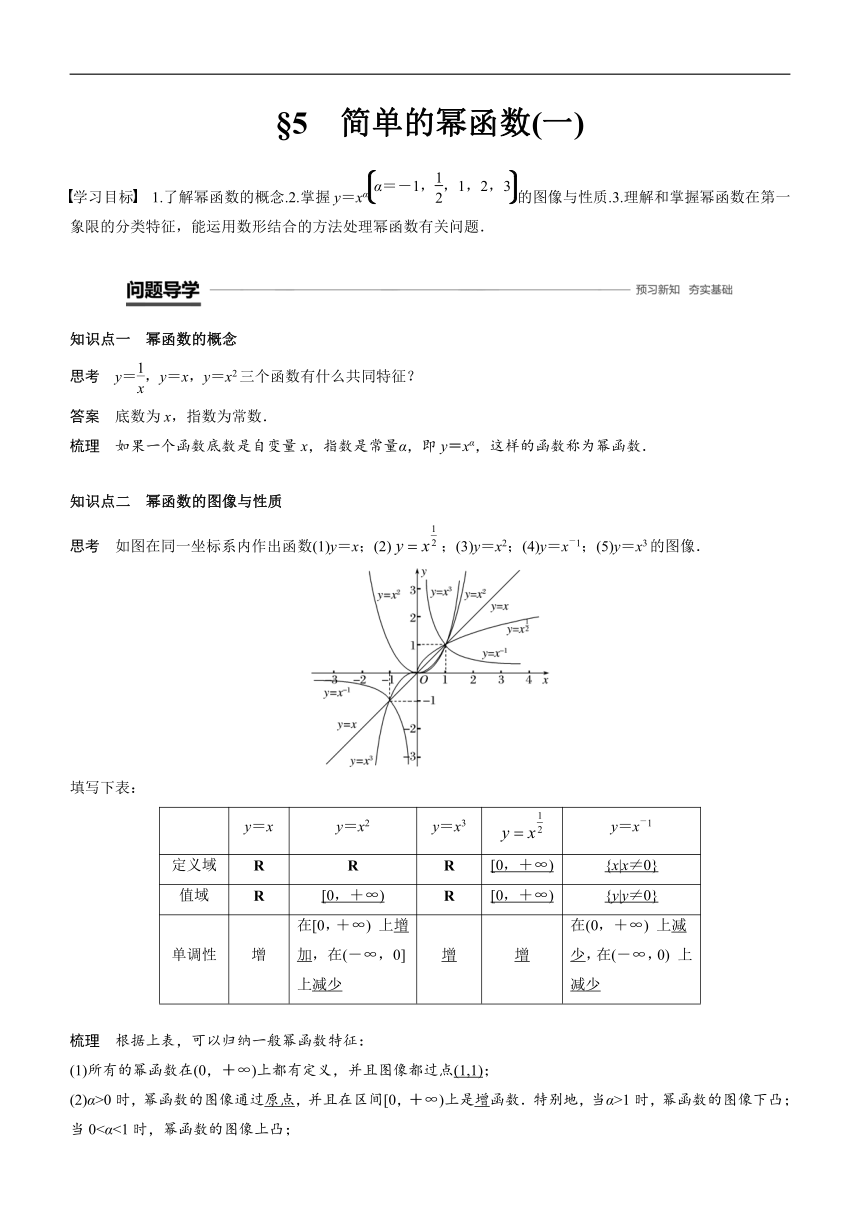 | |
| 格式 | zip | ||
| 文件大小 | 281.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 14:31:09 | ||
图片预览



文档简介
§5 简单的幂函数(一)
学习目标 1.了解幂函数的概念.2.掌握y=xα的图像与性质.3.理解和掌握幂函数在第一象限的分类特征,能运用数形结合的方法处理幂函数有关问题.
知识点一 幂函数的概念
思考 y=,y=x,y=x2三个函数有什么共同特征?
答案 底数为x,指数为常数.
梳理 如果一个函数底数是自变量x,指数是常量α,即y=xα,这样的函数称为幂函数.
知识点二 幂函数的图像与性质
思考 如图在同一坐标系内作出函数(1)y=x;(2);(3)y=x2;(4)y=x-1;(5)y=x3的图像.
填写下表:
y=x
y=x2
y=x3
y=x-1
定义域
R
R
R
[0,+∞)
{x|x≠0}
值域
R
[0,+∞)
R
[0,+∞)
{y|y≠0}
单调性
增
在[0,+∞)
上增加,在(-∞,0]
上减少
增
增
在(0,+∞)
上减少,在(-∞,0)
上减少
梳理 根据上表,可以归纳一般幂函数特征:
(1)所有的幂函数在(0,+∞)上都有定义,并且图像都过点(1,1);
(2)α>0时,幂函数的图像通过原点,并且在区间[0,+∞)上是增函数.特别地,当α>1时,幂函数的图像下凸;当0<α<1时,幂函数的图像上凸;
(3)α<0时,幂函数的图像在区间(0,+∞)上是减函数;
(4)幂指数互为倒数的幂函数在第一象限内的图像关于直线y=x对称;
(5)在第一象限,作直线x=a(a>1),它同各幂函数图像相交,按交点从下到上的顺序,幂指数按从小到大的顺序排列.
1.y=-是幂函数.( × )
2.当x∈(0,1)时,x2>x3.( √ )
3.与定义域相同.( × )
4.若y=xα在(0,+∞)上为增函数,则α>0.( √ )
类型一 幂函数的概念
例1 已知是幂函数,求m,n的值.
考点
题点
解 由题意得解得
所以m=-3或1,n=.
反思与感悟 只有满足函数解析式右边的系数为1,底数为自变量x,指数为常量这三个条件,才是幂函数.如:y=3x2,y=(2x)3,y=4都不是幂函数.
跟踪训练1 在函数y=,y=2x2,y=x2+x,y=1中,幂函数的个数为( )
A.0
B.1
C.2
D.3
考点
题点
答案 B
解析 因为y==x-2,所以是幂函数;
y=2x2由于出现系数2,因此不是幂函数;
y=x2+x是两项和的形式,不是幂函数;y=1=x0(x≠0),可以看出,常函数y=1的图像比幂函数y=x0的图像多了一个点(0,1),
所以常函数y=1不是幂函数.
类型二 幂函数的图像及应用
例2 若点(,2)在幂函数f(x)的图像上,点在幂函数g(x)的图像上,问当x为何值时,(1)f(x)>g(x);(2)f(x)=g(x);(3)f(x)考点
题点
解 设f(x)=xα,因为点(,2)在幂函数f(x)的图像上,所以将点(,2)代入f(x)=xα中,得2=()α,解得α=2,则f(x)=x2.
同理可求得g(x)=x-2.
在同一坐标系内作出函数f(x)=x2和g(x)=x-2的图像(如图所示),观察图像可得:
(1)当x>1或x<-1时,f(x)>g(x);
(2)当x=1或x=-1时,f(x)=g(x);
(3)当-1反思与感悟 幂函数由于指数α的不同,它们的定义域也不同,性质也不同,幂函数的图像主要分0<α<1,α>1和α<0三种情况讨论.
跟踪训练2 幂函数y=xα(α≠0),当α取不同的正数时,在区间[0,1]上它们的图像是一簇美丽的曲线(如图).设点A(1,0),B(0,1),连接AB,线段AB恰好被其中的两个幂函数y=xα,y=xβ的图像三等分,即有BM=MN=NA,则αβ等于( )
A.1
B.2
C.3
D.无法确定
考点
题点
答案 A
解析 由条件知,M,N,
∴=α,=β,
∴αβ=α=α=,∴αβ=1.故选A.
类型三 幂函数性质的应用
命题角度1 比较大小
例3 设则a,b,c的大小关系是( )
A.a>b>c
B.b>a>c
C.b>c>a
D.c>b>a
考点 比较幂值的大小
题点 利用单调性比较大小
答案 B
解析 ∵y=x在R上为减函数,∴即a∴即a>c.∴b>a>c.故选B.
反思与感悟 此类题在构建函数模型时要注意幂函数的特点:指数不变.比较大小的问题主要是利用函数的单调性,特别是要善于应用“搭桥”法进行分组,常数0和1是常用的中间量.
跟踪训练3 比较下列各组数中两个数的大小:
(1)0.3与0.3;
(2)-1与-1;
(3)0.3与
考点 比较幂值的大小
题点 利用中间值比较大小
解 (1)∵0<0.3<1,
∴y=x0.3在(0,+∞)上为增函数.
又>,∴0.3>0.3.
(2)∵y=x-1在(-∞,0)上是减函数,
又-<-,∴-1>-1.
(3)∵y=x0.3在(0,+∞)上为增函数,
∴由>0.3,可得0.3>0.30.3.①
又y=0.3x在(-∞,+∞)上为减函数,
∴0.30.3>②
由①②知0.3>
命题角度2 幂函数性质的综合应用
例4 已知幂函数y=x3m-9
(m∈N+)的图像关于y轴对称且在(0,+∞)上单调递减,求满足的a的取值范围.
考点 幂函数的性质
题点 利用幂函数的性质解不等式
解 因为函数在(0,+∞)上单调递减,所以3m-9<0,
解得m<3.又因为m∈N+,所以m=1,2.
因为函数的图像关于y轴对称,
所以3m-9为偶数,故m=1.
则原不等式可化为
因为在(-∞,0),(0,+∞)上单调递减,
所以a+1>3-2a>0或3-2a解得故a的取值范围是.
反思与感悟 幂函数y=xα中只有一个参数α,幂函数的所有性质都与α的取值有关,故可由α确定幂函数的定义域、值域、单调性、奇偶性,也可由这些性质去限制α的取值.
跟踪训练4 已知幂函数
(m∈N+).
(1)试确定该函数的定义域,并指明该函数在其定义域上的单调性;
(2)若函数还经过(2,),试确定m的值,并求满足f(2-a)>f(a-1)的实数a的取值范围.
考点 幂函数的性质
题点 利用幂函数的性质解不等式
解 (1)∵m∈N+,
∴m2+m=m(m+1)为偶数.
令m2+m=2k,k∈N+,则f(x)=,
∴定义域为[0,+∞),在[0,+∞)上f(x)为增函数.
(2)∵∴m2+m=2,
解得m=1或m=-2(舍去),
∴
由(1)知f(x)在定义域[0,+∞)上为增函数,
∴f(2-a)>f(a-1)等价于2-a>a-1≥0,
解得1≤a<.
1.已知幂函数f(x)=k·xα的图像过点,则k+α等于( )
A.
B.1
C.
D.2
考点 幂函数概念
题点 求幂函数解析式
答案 C
解析 由幂函数的定义知k=1.又f=,
所以α=,解得α=,从而k+α=.
2.已知幂函数f(x)的图像经过点,则f(4)的值等于( )
A.16
B.
C.2
D.
考点 幂函数概念
题点 求幂函数解析式
答案 D
3.设α∈,则使函数y=xα的定义域为R的所有α的值为( )
A.1,3
B.-1,1
C.-1,3
D.-1,1,3
考点 幂函数性质
题点 幂函数定义域
答案 A
4.下列是的图像的是( )
考点 幂函数图像
题点 根据解析式选函数图像
答案 B
5.以下结论正确的是( )
A.当α=0时,函数y=xα的图像是一条直线
B.幂函数的图像都经过(0,0),(1,1)两点
C.若幂函数y=xα的图像关于原点对称,则y=xα在定义域内y随x的增大而增大
D.幂函数的图像不可能在第四象限,但可能在第二象限
考点 幂函数性质
题点 幂函数性质
答案 D
1.幂函数y=xα(α∈R),其中α为常数,其本质特征是以幂的底x为自变量,指数α为常数,这是判断一个函数是不是幂函数的重要依据和唯一标准.
2.幂函数y=xα的图像与性质由于α的值不同而比较复杂,一般从两个方面考查:(1)α>0时,图像过(0,0),(1,1)在第一象限的图像上升;α<0时,图像不过原点,在第一象限的图像下降,反之也成立.(2)曲线在第一象限的凹凸性:α>1时,曲线下凸;0<α<1时,曲线上凸;α<0时,曲线下凸.
3.在具体应用时,不一定是y=xα,α=-1,,1,2,3这五个已研究熟的幂函数,这时可根据需要构造幂函数,并针对性地研究某一方面的性质.
2
学习目标 1.了解幂函数的概念.2.掌握y=xα的图像与性质.3.理解和掌握幂函数在第一象限的分类特征,能运用数形结合的方法处理幂函数有关问题.
知识点一 幂函数的概念
思考 y=,y=x,y=x2三个函数有什么共同特征?
答案 底数为x,指数为常数.
梳理 如果一个函数底数是自变量x,指数是常量α,即y=xα,这样的函数称为幂函数.
知识点二 幂函数的图像与性质
思考 如图在同一坐标系内作出函数(1)y=x;(2);(3)y=x2;(4)y=x-1;(5)y=x3的图像.
填写下表:
y=x
y=x2
y=x3
y=x-1
定义域
R
R
R
[0,+∞)
{x|x≠0}
值域
R
[0,+∞)
R
[0,+∞)
{y|y≠0}
单调性
增
在[0,+∞)
上增加,在(-∞,0]
上减少
增
增
在(0,+∞)
上减少,在(-∞,0)
上减少
梳理 根据上表,可以归纳一般幂函数特征:
(1)所有的幂函数在(0,+∞)上都有定义,并且图像都过点(1,1);
(2)α>0时,幂函数的图像通过原点,并且在区间[0,+∞)上是增函数.特别地,当α>1时,幂函数的图像下凸;当0<α<1时,幂函数的图像上凸;
(3)α<0时,幂函数的图像在区间(0,+∞)上是减函数;
(4)幂指数互为倒数的幂函数在第一象限内的图像关于直线y=x对称;
(5)在第一象限,作直线x=a(a>1),它同各幂函数图像相交,按交点从下到上的顺序,幂指数按从小到大的顺序排列.
1.y=-是幂函数.( × )
2.当x∈(0,1)时,x2>x3.( √ )
3.与定义域相同.( × )
4.若y=xα在(0,+∞)上为增函数,则α>0.( √ )
类型一 幂函数的概念
例1 已知是幂函数,求m,n的值.
考点
题点
解 由题意得解得
所以m=-3或1,n=.
反思与感悟 只有满足函数解析式右边的系数为1,底数为自变量x,指数为常量这三个条件,才是幂函数.如:y=3x2,y=(2x)3,y=4都不是幂函数.
跟踪训练1 在函数y=,y=2x2,y=x2+x,y=1中,幂函数的个数为( )
A.0
B.1
C.2
D.3
考点
题点
答案 B
解析 因为y==x-2,所以是幂函数;
y=2x2由于出现系数2,因此不是幂函数;
y=x2+x是两项和的形式,不是幂函数;y=1=x0(x≠0),可以看出,常函数y=1的图像比幂函数y=x0的图像多了一个点(0,1),
所以常函数y=1不是幂函数.
类型二 幂函数的图像及应用
例2 若点(,2)在幂函数f(x)的图像上,点在幂函数g(x)的图像上,问当x为何值时,(1)f(x)>g(x);(2)f(x)=g(x);(3)f(x)
题点
解 设f(x)=xα,因为点(,2)在幂函数f(x)的图像上,所以将点(,2)代入f(x)=xα中,得2=()α,解得α=2,则f(x)=x2.
同理可求得g(x)=x-2.
在同一坐标系内作出函数f(x)=x2和g(x)=x-2的图像(如图所示),观察图像可得:
(1)当x>1或x<-1时,f(x)>g(x);
(2)当x=1或x=-1时,f(x)=g(x);
(3)当-1
跟踪训练2 幂函数y=xα(α≠0),当α取不同的正数时,在区间[0,1]上它们的图像是一簇美丽的曲线(如图).设点A(1,0),B(0,1),连接AB,线段AB恰好被其中的两个幂函数y=xα,y=xβ的图像三等分,即有BM=MN=NA,则αβ等于( )
A.1
B.2
C.3
D.无法确定
考点
题点
答案 A
解析 由条件知,M,N,
∴=α,=β,
∴αβ=α=α=,∴αβ=1.故选A.
类型三 幂函数性质的应用
命题角度1 比较大小
例3 设则a,b,c的大小关系是( )
A.a>b>c
B.b>a>c
C.b>c>a
D.c>b>a
考点 比较幂值的大小
题点 利用单调性比较大小
答案 B
解析 ∵y=x在R上为减函数,∴即a
反思与感悟 此类题在构建函数模型时要注意幂函数的特点:指数不变.比较大小的问题主要是利用函数的单调性,特别是要善于应用“搭桥”法进行分组,常数0和1是常用的中间量.
跟踪训练3 比较下列各组数中两个数的大小:
(1)0.3与0.3;
(2)-1与-1;
(3)0.3与
考点 比较幂值的大小
题点 利用中间值比较大小
解 (1)∵0<0.3<1,
∴y=x0.3在(0,+∞)上为增函数.
又>,∴0.3>0.3.
(2)∵y=x-1在(-∞,0)上是减函数,
又-<-,∴-1>-1.
(3)∵y=x0.3在(0,+∞)上为增函数,
∴由>0.3,可得0.3>0.30.3.①
又y=0.3x在(-∞,+∞)上为减函数,
∴0.30.3>②
由①②知0.3>
命题角度2 幂函数性质的综合应用
例4 已知幂函数y=x3m-9
(m∈N+)的图像关于y轴对称且在(0,+∞)上单调递减,求满足的a的取值范围.
考点 幂函数的性质
题点 利用幂函数的性质解不等式
解 因为函数在(0,+∞)上单调递减,所以3m-9<0,
解得m<3.又因为m∈N+,所以m=1,2.
因为函数的图像关于y轴对称,
所以3m-9为偶数,故m=1.
则原不等式可化为
因为在(-∞,0),(0,+∞)上单调递减,
所以a+1>3-2a>0或3-2a
反思与感悟 幂函数y=xα中只有一个参数α,幂函数的所有性质都与α的取值有关,故可由α确定幂函数的定义域、值域、单调性、奇偶性,也可由这些性质去限制α的取值.
跟踪训练4 已知幂函数
(m∈N+).
(1)试确定该函数的定义域,并指明该函数在其定义域上的单调性;
(2)若函数还经过(2,),试确定m的值,并求满足f(2-a)>f(a-1)的实数a的取值范围.
考点 幂函数的性质
题点 利用幂函数的性质解不等式
解 (1)∵m∈N+,
∴m2+m=m(m+1)为偶数.
令m2+m=2k,k∈N+,则f(x)=,
∴定义域为[0,+∞),在[0,+∞)上f(x)为增函数.
(2)∵∴m2+m=2,
解得m=1或m=-2(舍去),
∴
由(1)知f(x)在定义域[0,+∞)上为增函数,
∴f(2-a)>f(a-1)等价于2-a>a-1≥0,
解得1≤a<.
1.已知幂函数f(x)=k·xα的图像过点,则k+α等于( )
A.
B.1
C.
D.2
考点 幂函数概念
题点 求幂函数解析式
答案 C
解析 由幂函数的定义知k=1.又f=,
所以α=,解得α=,从而k+α=.
2.已知幂函数f(x)的图像经过点,则f(4)的值等于( )
A.16
B.
C.2
D.
考点 幂函数概念
题点 求幂函数解析式
答案 D
3.设α∈,则使函数y=xα的定义域为R的所有α的值为( )
A.1,3
B.-1,1
C.-1,3
D.-1,1,3
考点 幂函数性质
题点 幂函数定义域
答案 A
4.下列是的图像的是( )
考点 幂函数图像
题点 根据解析式选函数图像
答案 B
5.以下结论正确的是( )
A.当α=0时,函数y=xα的图像是一条直线
B.幂函数的图像都经过(0,0),(1,1)两点
C.若幂函数y=xα的图像关于原点对称,则y=xα在定义域内y随x的增大而增大
D.幂函数的图像不可能在第四象限,但可能在第二象限
考点 幂函数性质
题点 幂函数性质
答案 D
1.幂函数y=xα(α∈R),其中α为常数,其本质特征是以幂的底x为自变量,指数α为常数,这是判断一个函数是不是幂函数的重要依据和唯一标准.
2.幂函数y=xα的图像与性质由于α的值不同而比较复杂,一般从两个方面考查:(1)α>0时,图像过(0,0),(1,1)在第一象限的图像上升;α<0时,图像不过原点,在第一象限的图像下降,反之也成立.(2)曲线在第一象限的凹凸性:α>1时,曲线下凸;0<α<1时,曲线上凸;α<0时,曲线下凸.
3.在具体应用时,不一定是y=xα,α=-1,,1,2,3这五个已研究熟的幂函数,这时可根据需要构造幂函数,并针对性地研究某一方面的性质.
2
