2019年数学同步必修一北师大版:第二章 映射 课时对点练(解析版)
文档属性
| 名称 | 2019年数学同步必修一北师大版:第二章 映射 课时对点练(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 99.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 14:33:18 | ||
图片预览


文档简介
2.2 函数的表示法(二)
2.3 映 射
一、选择题
1.设函数f(x)=若f(α)=4,则实数α等于( )
A.-4或-2
B.-4或2
C.-2或4
D.-2或2
2.已知函数f(n)=则f(5)的值是( )
A.4
B.48
C.240
D.1
440
3.已知f(x)=则f(f(f(-2)))等于( )
A.π
B.0
C.2
D.π+1
4.已知函数f(x)=若f(f(x))=2,则x的取值范围是( )
A.
B.[-1,1]
C.(-∞,-1)∪(1,+∞)
D.{2}∪[-1,1]
5.某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水不超过10立方米的,按每立方米m元收费;用水超过10立方米的,超过部分按每立方米2m元收费.某职工某月缴水费16m元,则该职工这个月实际用水为( )
A.13立方米
B.14立方米
C.18立方米
D.26立方米
6.著名的Dirichlet函数D(x)=则D(D(x))等于( )
A.0
B.1
C.
D.
7.若集合A={a,b,c},B={d,e},则从A到B可以建立不同的映射个数为( )
A.5
B.6
C.8
D.9
二、填空题
8.函数f(x)=的定义域是________.
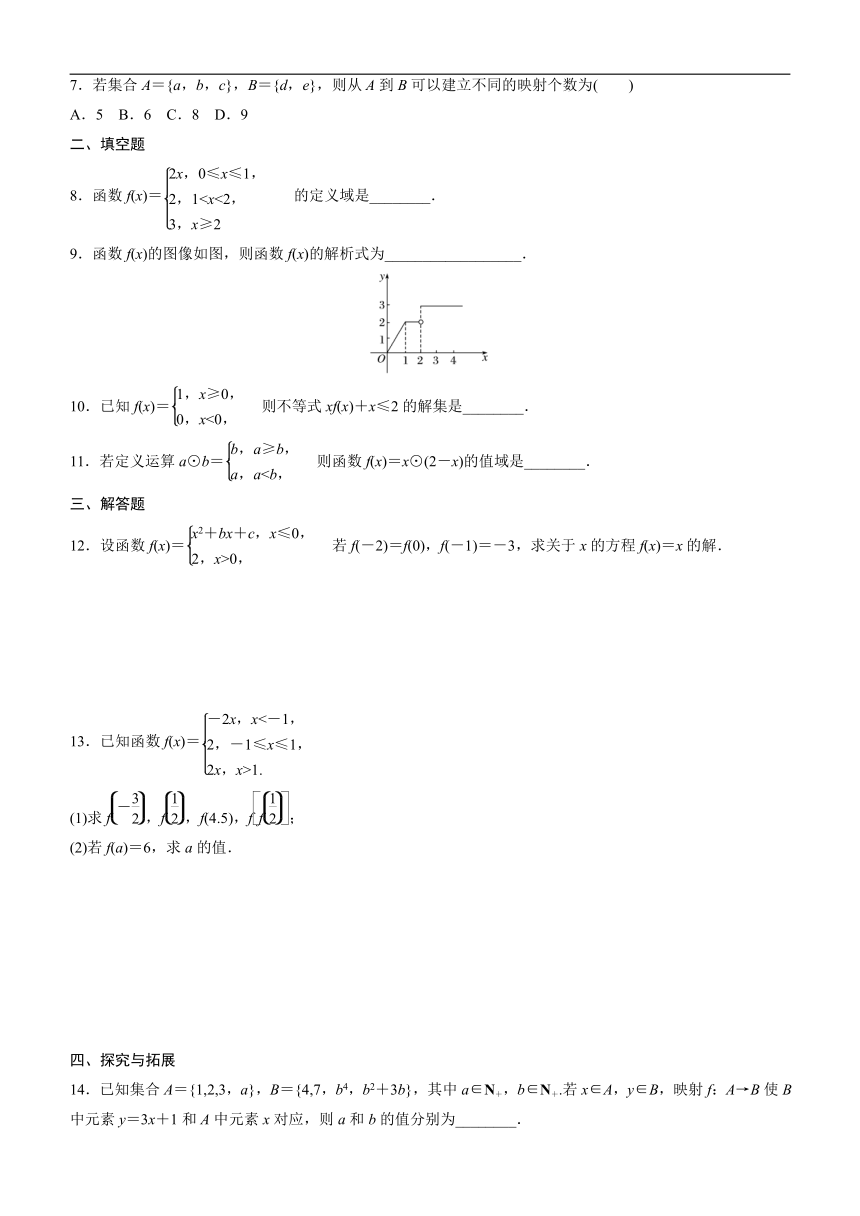
9.函数f(x)的图像如图,则函数f(x)的解析式为__________________.
10.已知f(x)=则不等式xf(x)+x≤2的解集是________.
11.若定义运算a⊙b=则函数f(x)=x⊙(2-x)的值域是________.
三、解答题
12.设函数f(x)=若f(-2)=f(0),f(-1)=-3,求关于x的方程f(x)=x的解.
13.已知函数f(x)=
(1)求f,f,f(4.5),f;
(2)若f(a)=6,求a的值.
四、探究与拓展
14.已知集合A={1,2,3,a},B={4,7,b4,b2+3b},其中a∈N+,b∈N+.若x∈A,y∈B,映射f:A→B使B中元素y=3x+1和A中元素x对应,则a和b的值分别为________.
15.已知函数f(x)=|x-3|-|x+1|.
(1)求f(x)的值域;
(2)解不等式:f(x)>0;
(3)若直线y=a与f(x)的图像无交点,求实数a的取值范围.
答案
1.
考点 分段函数
题点 分段函数求值
答案 B
解析 当α≤0时,由f(α)=-α=4,得α=-4;
当α>0时,f(α)=α2=4,得α=2.∴α=-4或α=2.
2.
考点 分段函数
题点 分段函数求值
答案 C
解析 因为f(n)=
所以f(5)=5f(4)=5×4f(3)=5×4×3f(2)=5×4×3×2f(1)=5×4×3×2×1×f(0)=5×4×3×2×1×2=240.故选C.
3.
考点 分段函数
题点 分段函数求值
答案 D
解析 f(-2)=0,f(0)=π,f(π)=π+1
4.
考点 分段函数
题点 分段函数求值
答案 D
解析 若x∈[-1,1],则f(x)=2,f(f(x))=f(2)=2,符合题意;若x>1,则f(x)=x,f(f(x))=f(x)=x=2,此时只有x=2符合题意;若x<-1,则f(x)=x,f(f(x))=f(x)=x=2,但因为x<-1,此时没有x符合题意.
5.
考点 分段函数
题点 分段函数应用问题
答案 A
解析 该单位职工每月应缴水费y与实际用水量x满足的关系式为y=
由y=16m,可知x>10.
令2mx-10m=16m,解得x=13(立方米).
6.
考点 分段函数
题点 分段函数求值
答案 B
解析 ∵D(x)∈{0,1},∴D(x)为有理数,
∴D(D(x))=1.
7.
答案 C
解析 用树状图写出所有的映射为:
a→d a→e共8个.
8.
考点 分段函数
题点 分段函数的定义域、值域
答案 [0,+∞)
解析 定义域为[0,1]∪(1,2)∪[2,+∞)=[0,+∞).
9.
考点 分段函数
题点 求分段函数解析式
答案 f(x)=
解析 当0≤x≤1时,设f(x)=kx,代入(1,2),得k=2,
∴f(x)=2x.
当1当x≥2时,f(x)=3,
∴f(x)=
10.
考点 分段函数
题点 分段函数与不等式结合
答案 {x|x≤1}
解析 当x≥0时,f(x)=1,代入xf(x)+x≤2,解得x≤1,∴0≤x≤1;当x<0时,f(x)=0,代入xf(x)+x≤2,解得x≤2,∴x<0.综上可知x≤1.
11.
考点 分段函数
题点 分段函数的定义域、值域
答案 (-∞,1]
解析 由题意知f(x)=
画出图像为
由图易得函数f(x)的值域为(-∞,1].
12.
考点 分段函数
题点 分段函数求值
解 ∵当x≤0时,f(x)=x2+bx+c,
∴f(-2)=(-2)2-2b+c,
f(0)=c,
f(-1)=(-1)2-b+c.
∵f(-2)=f(0),f(-1)=-3,
∴
解得
则f(x)=
当x≤0时,由f(x)=x,得x2+2x-2=x,
得x=-2或x=1.
由于x=1>0,故舍去.
当x>0时,由f(x)=x得x=2,
∴方程f(x)=x的解为-2,2.
13.
考点 分段函数
题点 分段函数求值
解 (1)∵-∈(-∞,-1),
∴f=-2×=3.
∵∈[-1,1],∴f=2.
又2∈(1,+∞),∴f=f(2)=2×2=4.
∵4.5∈(1,+∞),∴f(4.5)=2×4.5=9.
(2)经观察可知a [-1,1],否则f(a)=2.
若a∈(-∞,-1),令-2a=6,得a=-3,符合题意;
若a∈(1,+∞),令2a=6,得a=3,符合题意.
∴a的值为-3或3.
14.
考点 映射的概念
题点 映射中的参数问题
答案 5,2
解析 ∵A中元素x对应B中元素y=3x+1,∴A中元素1的像是4,2的像是7,3的像是10,∴b4=10或b2+3b=10.又b∈N+,∴b2+3b=10,解得b=2.∵a的像b4=16,∴3a+1=16,解得a=5.
15.
考点 分段函数
题点 分段函数的综合应用
解 若x≤-1,则x-3<0,x+1≤0,
f(x)=-(x-3)+(x+1)=4;
若-10,
f(x)=-(x-3)-(x+1)=-2x+2;
若x>3,则x-3>0,x+1>0,
f(x)=(x-3)-(x+1)=-4.
∴f(x)=
(1)当-1∴f(x)的值域为[-4,4)∪{4}∪{-4}=[-4,4].
(2)f(x)>0,即①
或②
或③
解①得x≤-1,解②得-1∴f(x)>0的解集为(-∞,-1]∪(-1,1)∪ =(-∞,1).
(3)f(x)的图像如下:
由图可知,当a∈(-∞,-4)∪(4,+∞)时,直线y=a与f(x)的图像无交点.
2
2.3 映 射
一、选择题
1.设函数f(x)=若f(α)=4,则实数α等于( )
A.-4或-2
B.-4或2
C.-2或4
D.-2或2
2.已知函数f(n)=则f(5)的值是( )
A.4
B.48
C.240
D.1
440
3.已知f(x)=则f(f(f(-2)))等于( )
A.π
B.0
C.2
D.π+1
4.已知函数f(x)=若f(f(x))=2,则x的取值范围是( )
A.
B.[-1,1]
C.(-∞,-1)∪(1,+∞)
D.{2}∪[-1,1]
5.某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水不超过10立方米的,按每立方米m元收费;用水超过10立方米的,超过部分按每立方米2m元收费.某职工某月缴水费16m元,则该职工这个月实际用水为( )
A.13立方米
B.14立方米
C.18立方米
D.26立方米
6.著名的Dirichlet函数D(x)=则D(D(x))等于( )
A.0
B.1
C.
D.
7.若集合A={a,b,c},B={d,e},则从A到B可以建立不同的映射个数为( )
A.5
B.6
C.8
D.9
二、填空题
8.函数f(x)=的定义域是________.
9.函数f(x)的图像如图,则函数f(x)的解析式为__________________.
10.已知f(x)=则不等式xf(x)+x≤2的解集是________.
11.若定义运算a⊙b=则函数f(x)=x⊙(2-x)的值域是________.
三、解答题
12.设函数f(x)=若f(-2)=f(0),f(-1)=-3,求关于x的方程f(x)=x的解.
13.已知函数f(x)=
(1)求f,f,f(4.5),f;
(2)若f(a)=6,求a的值.
四、探究与拓展
14.已知集合A={1,2,3,a},B={4,7,b4,b2+3b},其中a∈N+,b∈N+.若x∈A,y∈B,映射f:A→B使B中元素y=3x+1和A中元素x对应,则a和b的值分别为________.
15.已知函数f(x)=|x-3|-|x+1|.
(1)求f(x)的值域;
(2)解不等式:f(x)>0;
(3)若直线y=a与f(x)的图像无交点,求实数a的取值范围.
答案
1.
考点 分段函数
题点 分段函数求值
答案 B
解析 当α≤0时,由f(α)=-α=4,得α=-4;
当α>0时,f(α)=α2=4,得α=2.∴α=-4或α=2.
2.
考点 分段函数
题点 分段函数求值
答案 C
解析 因为f(n)=
所以f(5)=5f(4)=5×4f(3)=5×4×3f(2)=5×4×3×2f(1)=5×4×3×2×1×f(0)=5×4×3×2×1×2=240.故选C.
3.
考点 分段函数
题点 分段函数求值
答案 D
解析 f(-2)=0,f(0)=π,f(π)=π+1
4.
考点 分段函数
题点 分段函数求值
答案 D
解析 若x∈[-1,1],则f(x)=2,f(f(x))=f(2)=2,符合题意;若x>1,则f(x)=x,f(f(x))=f(x)=x=2,此时只有x=2符合题意;若x<-1,则f(x)=x,f(f(x))=f(x)=x=2,但因为x<-1,此时没有x符合题意.
5.
考点 分段函数
题点 分段函数应用问题
答案 A
解析 该单位职工每月应缴水费y与实际用水量x满足的关系式为y=
由y=16m,可知x>10.
令2mx-10m=16m,解得x=13(立方米).
6.
考点 分段函数
题点 分段函数求值
答案 B
解析 ∵D(x)∈{0,1},∴D(x)为有理数,
∴D(D(x))=1.
7.
答案 C
解析 用树状图写出所有的映射为:
a→d a→e共8个.
8.
考点 分段函数
题点 分段函数的定义域、值域
答案 [0,+∞)
解析 定义域为[0,1]∪(1,2)∪[2,+∞)=[0,+∞).
9.
考点 分段函数
题点 求分段函数解析式
答案 f(x)=
解析 当0≤x≤1时,设f(x)=kx,代入(1,2),得k=2,
∴f(x)=2x.
当1
∴f(x)=
10.
考点 分段函数
题点 分段函数与不等式结合
答案 {x|x≤1}
解析 当x≥0时,f(x)=1,代入xf(x)+x≤2,解得x≤1,∴0≤x≤1;当x<0时,f(x)=0,代入xf(x)+x≤2,解得x≤2,∴x<0.综上可知x≤1.
11.
考点 分段函数
题点 分段函数的定义域、值域
答案 (-∞,1]
解析 由题意知f(x)=
画出图像为
由图易得函数f(x)的值域为(-∞,1].
12.
考点 分段函数
题点 分段函数求值
解 ∵当x≤0时,f(x)=x2+bx+c,
∴f(-2)=(-2)2-2b+c,
f(0)=c,
f(-1)=(-1)2-b+c.
∵f(-2)=f(0),f(-1)=-3,
∴
解得
则f(x)=
当x≤0时,由f(x)=x,得x2+2x-2=x,
得x=-2或x=1.
由于x=1>0,故舍去.
当x>0时,由f(x)=x得x=2,
∴方程f(x)=x的解为-2,2.
13.
考点 分段函数
题点 分段函数求值
解 (1)∵-∈(-∞,-1),
∴f=-2×=3.
∵∈[-1,1],∴f=2.
又2∈(1,+∞),∴f=f(2)=2×2=4.
∵4.5∈(1,+∞),∴f(4.5)=2×4.5=9.
(2)经观察可知a [-1,1],否则f(a)=2.
若a∈(-∞,-1),令-2a=6,得a=-3,符合题意;
若a∈(1,+∞),令2a=6,得a=3,符合题意.
∴a的值为-3或3.
14.
考点 映射的概念
题点 映射中的参数问题
答案 5,2
解析 ∵A中元素x对应B中元素y=3x+1,∴A中元素1的像是4,2的像是7,3的像是10,∴b4=10或b2+3b=10.又b∈N+,∴b2+3b=10,解得b=2.∵a的像b4=16,∴3a+1=16,解得a=5.
15.
考点 分段函数
题点 分段函数的综合应用
解 若x≤-1,则x-3<0,x+1≤0,
f(x)=-(x-3)+(x+1)=4;
若-1
f(x)=-(x-3)-(x+1)=-2x+2;
若x>3,则x-3>0,x+1>0,
f(x)=(x-3)-(x+1)=-4.
∴f(x)=
(1)当-1
(2)f(x)>0,即①
或②
或③
解①得x≤-1,解②得-1
(3)f(x)的图像如下:
由图可知,当a∈(-∞,-4)∪(4,+∞)时,直线y=a与f(x)的图像无交点.
2
