27.3 垂径定理 复习课件(14张PPT)
文档属性
| 名称 | 27.3 垂径定理 复习课件(14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 145.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 10:55:54 | ||
图片预览






文档简介
课件14张PPT。如图,是一木制圆形脸谱工艺品,鼻子是圆心,
A、B两点为脸谱的耳朵,打算在工艺品的反面
两耳连线中点D处打一小孔,现在只有一块无刻度
单位的直角三角板,请同学们帮助确定D的位置。 圆是轴对称图形,任意一条直
径所在的直线都是它的对称轴。垂径定理及其推论
复习课复习回顾 1、垂径定理:垂直于弦的直径平分弦,
并且平分弦所对的两条弧.·OABCDE推论:知二推二① 经过圆心② 垂直于弦 ③ 平分弦④ 平分弦所对的弧 根据垂径定理与推论可知:对于一个圆和一条直线来说,如果具备: 由四个条件中的任何两个条件都可以推出其他二个结论.1、如图,在⊙O中,CD是直径,AB是弦,且CD平分AB,已知CD = 20,AB = 16,则OM=_________
垂径定理基础应用本题知识点:
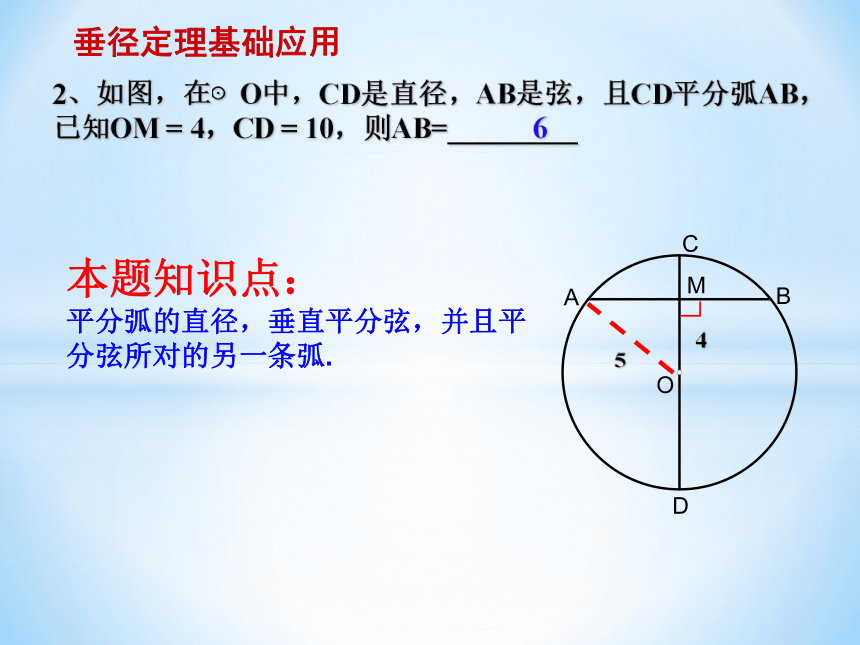
平分弦(这条弦不是直径)的直径垂直于弦,并且平分弦所对的两条弧.10862、如图,在⊙O中,CD是直径,AB是弦,且CD平分弧AB,已知OM = 4,CD = 10,则AB=_________
垂径定理基础应用本题知识点:
平分弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
4563.如图,弓形ACB中,弦AB的长为8厘米,弦的中点到劣弧中点间的长度是2厘米,则弓形所在圆的半径= . x42x-2本题知识点:平分弦及弦所对的一条弧的中点的直线必过圆心且垂直该弦.
垂径定理基础应用54.如图,CD垂直平分AB,若已知AC= ,CD=2,
这个弓形所在圆的半径是 .本题知识点:
垂直平分弦的直线必过圆心.垂径定理基础应用2455.弓形的弦长为16cm,弓形的高4cm,则这弓形所在的圆的半径为 . 本题知识点:
垂直弦且平分弦所对的弧的直线必过圆心且平分弦.垂径定理基础应用涉及圆中半径、弦长、弦心距的计算时,常通过作半径,作垂线构造直角三角形,利用垂径定理和勾股定理解决。48x-4x10cm372小试牛刀如图,在半径为6的⊙ O中,两弦AB ⊥ CD,垂足为E,CE=3,DE=7。
求:AB的长MN26实战演练:如图,在⊙ O中,弦AB、CD延长相交于点P,若AB=CD,
点E、点F分别是AB、CD中点。
求证:PE=PF34在圆的几何证明中,我们应勤观察,有效利用弦的中点或弧的中点去构造直角三角形。变式:如图,在⊙ O中,弦AB、CD延长相交于点P,M、N分别是弧AB、弧CD的中点,PQ平分∠APC
求证:PQ⊥MN
课堂小节谈谈本堂课你有什么收获作业:补充练习1.由于过度地采伐森林和破坏植被,使我国许多地区频频遭受
沙尘暴的侵袭.近日A市气象局测得沙尘暴中心在A市的正西方
向300km的B处,正以 km/h的速度向南偏东60°的BF方向
移动,距沙尘暴中心200km的范围内是受沙尘暴严重影响的区域.
(1)通过计算说明A市必然会受到这次沙尘暴的影响;
(2)计算A市受沙尘暴影响的时间.实际运用
A、B两点为脸谱的耳朵,打算在工艺品的反面
两耳连线中点D处打一小孔,现在只有一块无刻度
单位的直角三角板,请同学们帮助确定D的位置。 圆是轴对称图形,任意一条直
径所在的直线都是它的对称轴。垂径定理及其推论
复习课复习回顾 1、垂径定理:垂直于弦的直径平分弦,
并且平分弦所对的两条弧.·OABCDE推论:知二推二① 经过圆心② 垂直于弦 ③ 平分弦④ 平分弦所对的弧 根据垂径定理与推论可知:对于一个圆和一条直线来说,如果具备: 由四个条件中的任何两个条件都可以推出其他二个结论.1、如图,在⊙O中,CD是直径,AB是弦,且CD平分AB,已知CD = 20,AB = 16,则OM=_________
垂径定理基础应用本题知识点:
平分弦(这条弦不是直径)的直径垂直于弦,并且平分弦所对的两条弧.10862、如图,在⊙O中,CD是直径,AB是弦,且CD平分弧AB,已知OM = 4,CD = 10,则AB=_________
垂径定理基础应用本题知识点:
平分弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
4563.如图,弓形ACB中,弦AB的长为8厘米,弦的中点到劣弧中点间的长度是2厘米,则弓形所在圆的半径= . x42x-2本题知识点:平分弦及弦所对的一条弧的中点的直线必过圆心且垂直该弦.
垂径定理基础应用54.如图,CD垂直平分AB,若已知AC= ,CD=2,
这个弓形所在圆的半径是 .本题知识点:
垂直平分弦的直线必过圆心.垂径定理基础应用2455.弓形的弦长为16cm,弓形的高4cm,则这弓形所在的圆的半径为 . 本题知识点:
垂直弦且平分弦所对的弧的直线必过圆心且平分弦.垂径定理基础应用涉及圆中半径、弦长、弦心距的计算时,常通过作半径,作垂线构造直角三角形,利用垂径定理和勾股定理解决。48x-4x10cm372小试牛刀如图,在半径为6的⊙ O中,两弦AB ⊥ CD,垂足为E,CE=3,DE=7。
求:AB的长MN26实战演练:如图,在⊙ O中,弦AB、CD延长相交于点P,若AB=CD,
点E、点F分别是AB、CD中点。
求证:PE=PF34在圆的几何证明中,我们应勤观察,有效利用弦的中点或弧的中点去构造直角三角形。变式:如图,在⊙ O中,弦AB、CD延长相交于点P,M、N分别是弧AB、弧CD的中点,PQ平分∠APC
求证:PQ⊥MN
课堂小节谈谈本堂课你有什么收获作业:补充练习1.由于过度地采伐森林和破坏植被,使我国许多地区频频遭受
沙尘暴的侵袭.近日A市气象局测得沙尘暴中心在A市的正西方
向300km的B处,正以 km/h的速度向南偏东60°的BF方向
移动,距沙尘暴中心200km的范围内是受沙尘暴严重影响的区域.
(1)通过计算说明A市必然会受到这次沙尘暴的影响;
(2)计算A市受沙尘暴影响的时间.实际运用
