27.2(3) 圆心角、弧、弦、弦心距之间的关系 课件(8张PPT)
文档属性
| 名称 | 27.2(3) 圆心角、弧、弦、弦心距之间的关系 课件(8张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 55.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 00:00:00 | ||
图片预览


文档简介
(共8张PPT)
A
B
C
D
o
E
F
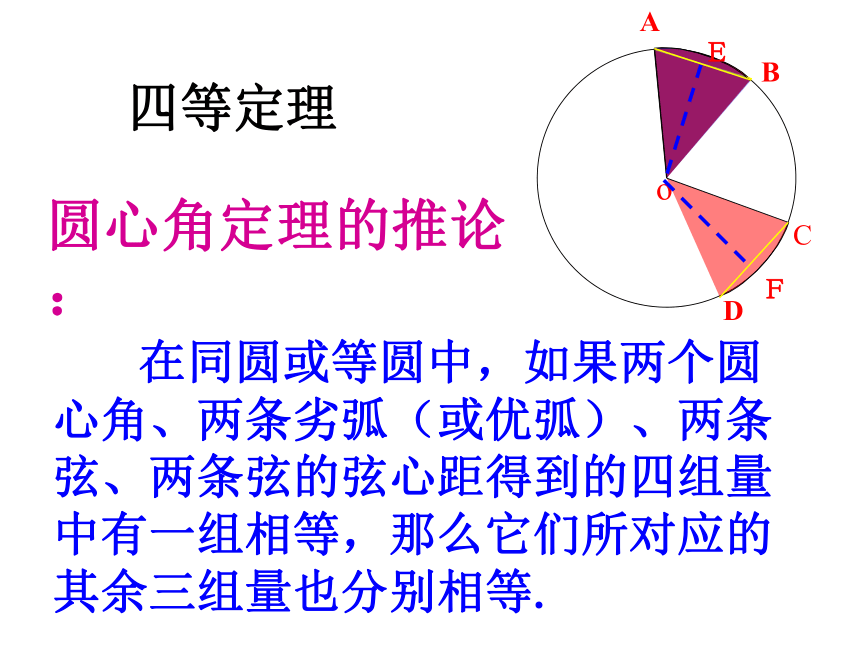
在同圆或等圆中,如果两个圆心角、两条劣弧(或优弧)、两条弦、两条弦的弦心距得到的四组量中有一组相等,那么它们所对应的其余三组量也分别相等.
圆心角定理的推论:
四等定理
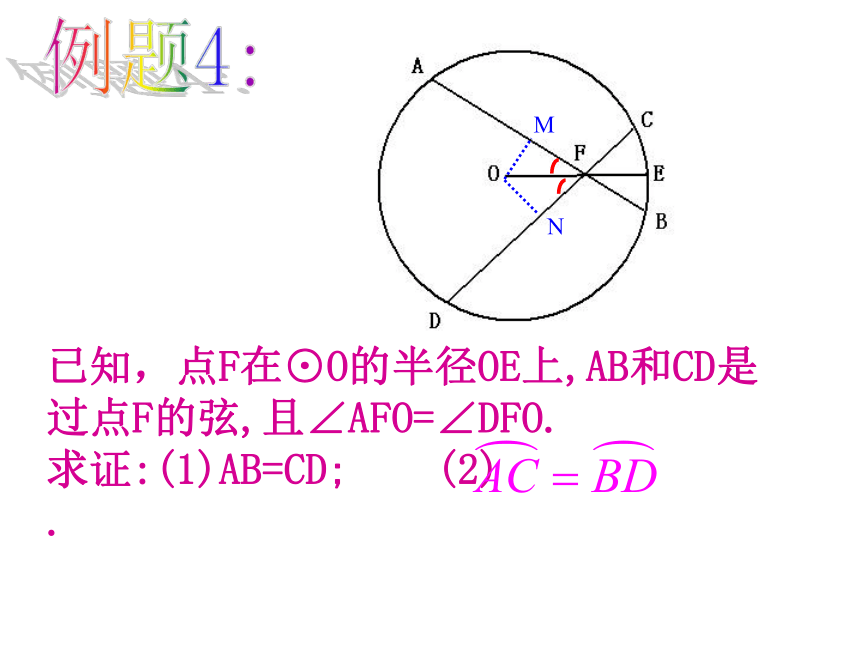
已知,点F在⊙O的半径OE上,AB和CD是过点F的弦,且∠AFO=∠DFO.
求证:(1)AB=CD;
(2)
.
M
N
已知,⊙O是△ABC的外接圆,AE平分△ABC的外角∠DAC,OM⊥AB,ON⊥AC,垂足分别是点M、N,且OM=ON.
求证:
(1)
AE∥BC;
(2)AO⊥AE.
已知,在⊙O中,AB、CD是⊙O的弦,且AB=CD.
求证:△ACB≌△DBC.
已知,AB是
⊙O的直径,AC和AD是分别位于AB两侧的两条相等的弦.
求证:AB平分∠CAD.
E
F
已知,⊙O的弦AB与CD相交于点E,AB=CD.
求证:AE=DE.
可证:△ABD≌△DCA
已知,⊙O的弦AB与CD相交于点P,OM⊥AB,ON
⊥
CD,垂足分别是点M、N,
且
.
求证(1)
∠OMN=
∠ONM
.(2)OP
⊥
MN.
A
B
C
D
o
E
F
在同圆或等圆中,如果两个圆心角、两条劣弧(或优弧)、两条弦、两条弦的弦心距得到的四组量中有一组相等,那么它们所对应的其余三组量也分别相等.
圆心角定理的推论:
四等定理
已知,点F在⊙O的半径OE上,AB和CD是过点F的弦,且∠AFO=∠DFO.
求证:(1)AB=CD;
(2)
.
M
N
已知,⊙O是△ABC的外接圆,AE平分△ABC的外角∠DAC,OM⊥AB,ON⊥AC,垂足分别是点M、N,且OM=ON.
求证:
(1)
AE∥BC;
(2)AO⊥AE.
已知,在⊙O中,AB、CD是⊙O的弦,且AB=CD.
求证:△ACB≌△DBC.
已知,AB是
⊙O的直径,AC和AD是分别位于AB两侧的两条相等的弦.
求证:AB平分∠CAD.
E
F
已知,⊙O的弦AB与CD相交于点E,AB=CD.
求证:AE=DE.
可证:△ABD≌△DCA
已知,⊙O的弦AB与CD相交于点P,OM⊥AB,ON
⊥
CD,垂足分别是点M、N,
且
.
求证(1)
∠OMN=
∠ONM
.(2)OP
⊥
MN.
