27.5 圆和圆的位置关系(1) 课件(18张PPT)
文档属性
| 名称 | 27.5 圆和圆的位置关系(1) 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 128.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 11:13:26 | ||
图片预览



文档简介
(共18张PPT)
27.5
圆和圆的位置关系(1)
操
作
演
示
.
O1
.
O2
.
O1
.
O2
操
作
演
示
.
O1
.
O2
操
作
演
示
.
O1
.
O2
操
作
演
示
.O1
.
O2
操
作
演
示
.
O1
.
O2
操
作
演
示
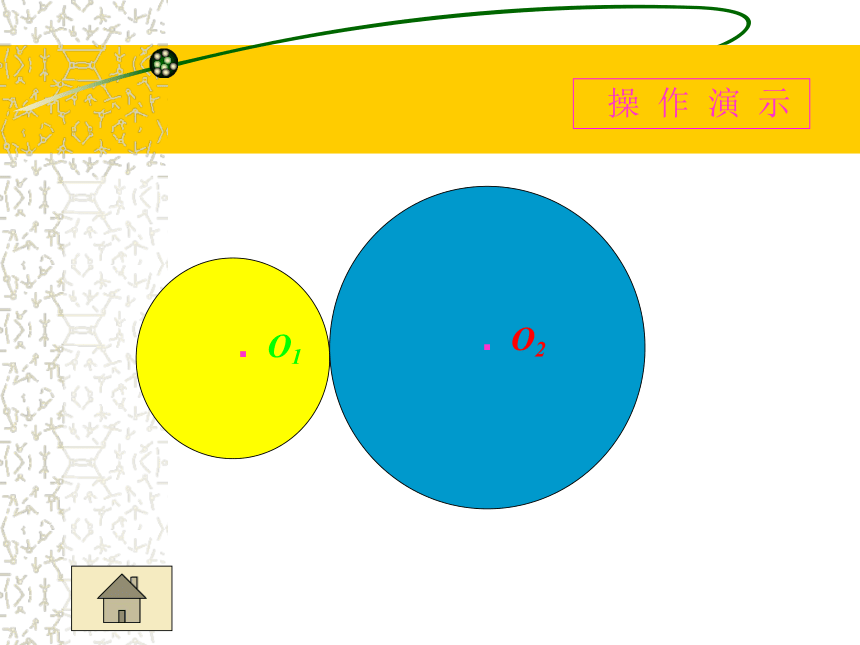
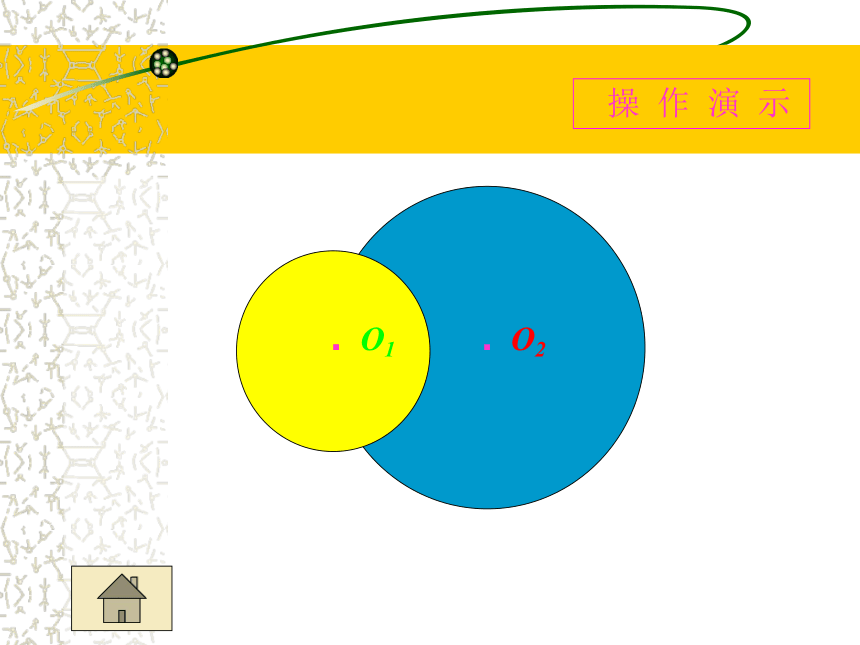
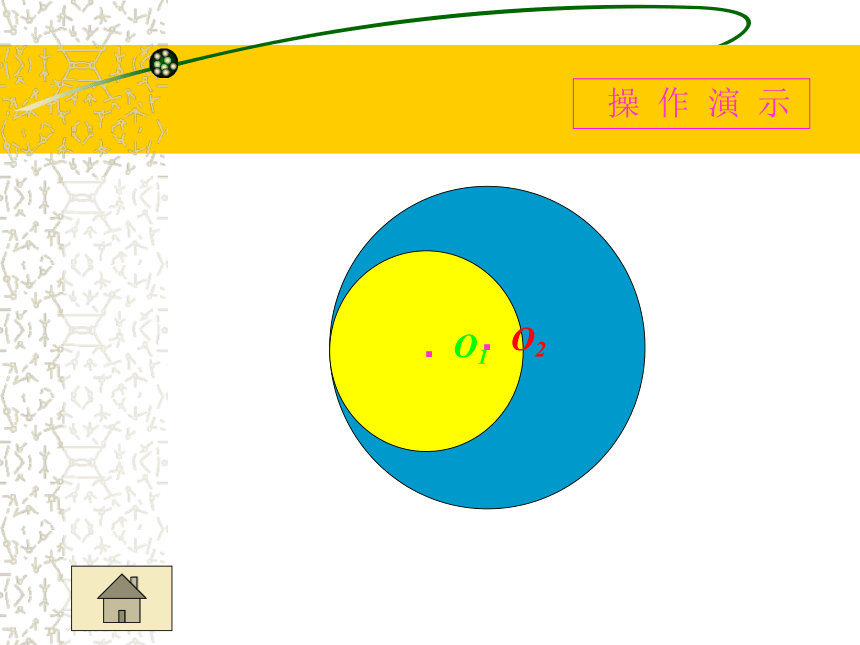
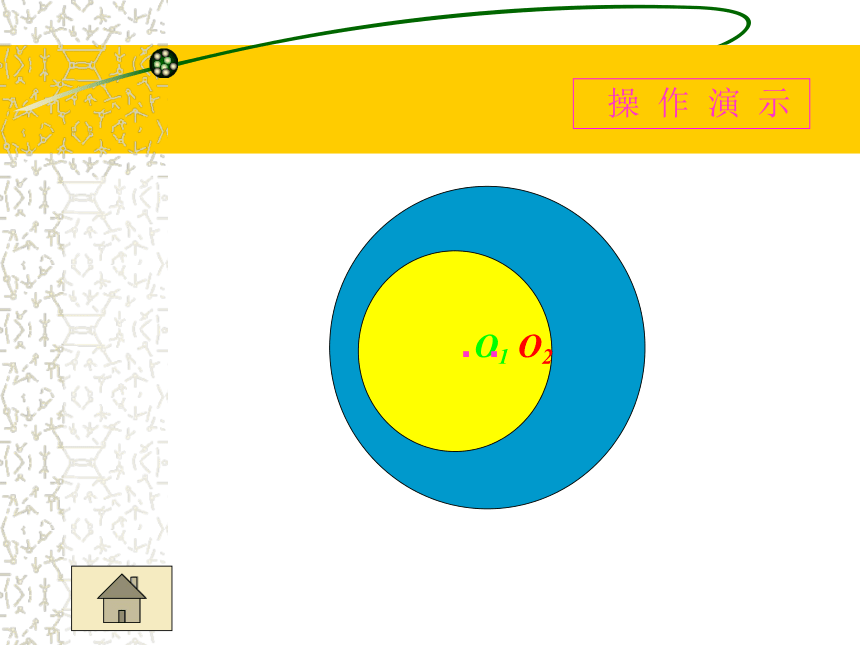
两圆公共点的个数
与
两圆的位置关系:
两圆没有公共点
两圆相离
两圆有唯一公共点
两圆相切
两圆有两个公共点
两圆相交
两圆外离
两圆内含
两圆外切
两圆内切
归
纳
总
结
两圆公共点的个数
与
两圆的位置关系:
两圆没有公共点
两圆相离
两圆有唯一公共点
两圆相切
两圆有两个公共点
两圆相交
两圆外离
两圆内含
两圆外切
两圆内切
归
纳
总
结
小
组
交
流
设⊙O1的半径为r1,
⊙O2的半径为r2
(r1
=
r2),圆心距(
O1
O2的长度)表示为
d
。请观察讨论两圆的五种位置分别与d
、
r1
、
r2三个量之间有什么联系?
外离
外切
相交
内切
内含
同心圆
(一种特殊的内含)
小
组
交
流
r2
r1
O
1
O
2
r2
r1
O
1
O
2
r2
r1
O
1
O
2
r2
r1
O
1
O
2
r2
r1
O
1
O
2
r2
r1
O
1
O
2
观察讨论d
与r1
、r2之间的关系
外离
外切
相交
内切
内含
同心圆
(一种特殊的内含)
小
组
交
流
r2
r1
O
1
O
2
r2
r1
O
1
O
2
r2
r1
O
1
O
2
r2
r1
O
1
O
2
r2
r1
O
1
O
2
r2
r1
O
1
O
2
d
>r1+r2
|r1-r2
|
<
d
<
r1+r2
0≤
d
<
|
r1
-
r2
|
d
=0
d
=r1+r2
0<
d
=
|
r1
-
r2
|
观察讨论d
与r1
、r2之间的关系
圆和圆的位置关系与这两圆的半径及圆心距(即两圆圆心的距离)的大小有关:
如果两圆半径分别为
r1
和
r2
,圆心距为d,那么
两圆外离
两圆外切
两圆相交
两圆内切
两圆内含
思考:当
r1
=
r2
时,两圆可能内含或内切吗?
归
纳
总
结
d
>r1+r2
d
=r1+r2
|r1-r2
|
<
d
<
r1+r2
0<
d
=
|
r1
-
r2
|
0≤
d
<
|
r1
-
r2
|
归
纳
总
结
0
内切
外切
内含
相交
外离
|r1
-
r2|
r1
+
r2
特殊记忆法
例1:已知⊙O1
和⊙O2
的半径长分别为3和4,
根据下列条件判断⊙O1
和⊙O2
的位置关系。
例
题
讲
解
(1)O1
O2
=
7
(2)O1
O2
=
4
(3)O1
O2
=
0.5
例2:已知⊙A
、⊙B
、⊙C
两两外切(如图),AB
=
3cm
,BC
=
5cm
,
AC
=
6cm
,
求这三个圆的
半径
。
A
C
B
例
题
讲
解
分析:
⊙A与⊙C,⊙B与⊙C
,⊙A与
⊙C都外切,称为三个圆两两外切。
根据两圆外切得d
=
r1
+
r2和同圆的半径相等,可以用代数方法列方程组解决。
例
题
讲
解
解:设⊙A
、
⊙B
、
⊙C的半径分别为x厘米、y厘米、z厘米。
因为⊙A
、
⊙B
、
⊙C两两外切,所以
x+
y=3
y+
z=5
z+
x=6
解得
x=2
y=1
z=4
所以⊙A
、⊙B
、⊙C的半径分别为2厘米、1厘米、4厘米。
小
结:
本节课有哪些收获?
交
流
小
结
27.5
圆和圆的位置关系(1)
操
作
演
示
.
O1
.
O2
.
O1
.
O2
操
作
演
示
.
O1
.
O2
操
作
演
示
.
O1
.
O2
操
作
演
示
.O1
.
O2
操
作
演
示
.
O1
.
O2
操
作
演
示
两圆公共点的个数
与
两圆的位置关系:
两圆没有公共点
两圆相离
两圆有唯一公共点
两圆相切
两圆有两个公共点
两圆相交
两圆外离
两圆内含
两圆外切
两圆内切
归
纳
总
结
两圆公共点的个数
与
两圆的位置关系:
两圆没有公共点
两圆相离
两圆有唯一公共点
两圆相切
两圆有两个公共点
两圆相交
两圆外离
两圆内含
两圆外切
两圆内切
归
纳
总
结
小
组
交
流
设⊙O1的半径为r1,
⊙O2的半径为r2
(r1
=
r2),圆心距(
O1
O2的长度)表示为
d
。请观察讨论两圆的五种位置分别与d
、
r1
、
r2三个量之间有什么联系?
外离
外切
相交
内切
内含
同心圆
(一种特殊的内含)
小
组
交
流
r2
r1
O
1
O
2
r2
r1
O
1
O
2
r2
r1
O
1
O
2
r2
r1
O
1
O
2
r2
r1
O
1
O
2
r2
r1
O
1
O
2
观察讨论d
与r1
、r2之间的关系
外离
外切
相交
内切
内含
同心圆
(一种特殊的内含)
小
组
交
流
r2
r1
O
1
O
2
r2
r1
O
1
O
2
r2
r1
O
1
O
2
r2
r1
O
1
O
2
r2
r1
O
1
O
2
r2
r1
O
1
O
2
d
>r1+r2
|r1-r2
|
<
d
<
r1+r2
0≤
d
<
|
r1
-
r2
|
d
=0
d
=r1+r2
0<
d
=
|
r1
-
r2
|
观察讨论d
与r1
、r2之间的关系
圆和圆的位置关系与这两圆的半径及圆心距(即两圆圆心的距离)的大小有关:
如果两圆半径分别为
r1
和
r2
,圆心距为d,那么
两圆外离
两圆外切
两圆相交
两圆内切
两圆内含
思考:当
r1
=
r2
时,两圆可能内含或内切吗?
归
纳
总
结
d
>r1+r2
d
=r1+r2
|r1-r2
|
<
d
<
r1+r2
0<
d
=
|
r1
-
r2
|
0≤
d
<
|
r1
-
r2
|
归
纳
总
结
0
内切
外切
内含
相交
外离
|r1
-
r2|
r1
+
r2
特殊记忆法
例1:已知⊙O1
和⊙O2
的半径长分别为3和4,
根据下列条件判断⊙O1
和⊙O2
的位置关系。
例
题
讲
解
(1)O1
O2
=
7
(2)O1
O2
=
4
(3)O1
O2
=
0.5
例2:已知⊙A
、⊙B
、⊙C
两两外切(如图),AB
=
3cm
,BC
=
5cm
,
AC
=
6cm
,
求这三个圆的
半径
。
A
C
B
例
题
讲
解
分析:
⊙A与⊙C,⊙B与⊙C
,⊙A与
⊙C都外切,称为三个圆两两外切。
根据两圆外切得d
=
r1
+
r2和同圆的半径相等,可以用代数方法列方程组解决。
例
题
讲
解
解:设⊙A
、
⊙B
、
⊙C的半径分别为x厘米、y厘米、z厘米。
因为⊙A
、
⊙B
、
⊙C两两外切,所以
x+
y=3
y+
z=5
z+
x=6
解得
x=2
y=1
z=4
所以⊙A
、⊙B
、⊙C的半径分别为2厘米、1厘米、4厘米。
小
结:
本节课有哪些收获?
交
流
小
结
