28.3(2)表示一组数据平均水平的量 课件(19张)
文档属性
| 名称 | 28.3(2)表示一组数据平均水平的量 课件(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 197.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
§28.3表示一组数据平均水平的量(2)
一.复习引入
提问1:平均数的计算公式是什么
1.一般地,如果一组数据
,
它们的平均数记作
,则
2.若
个数
都在常数
附近波动,那
么
,
,
…
,
记
可得平均数计算公式:
提问2:加权平均数的计算公式是什么?
如果在一组数据
中分别出现次数分别为
,
记
,
,
则
其中
叫做权,
叫做这 个数的加权平均数.
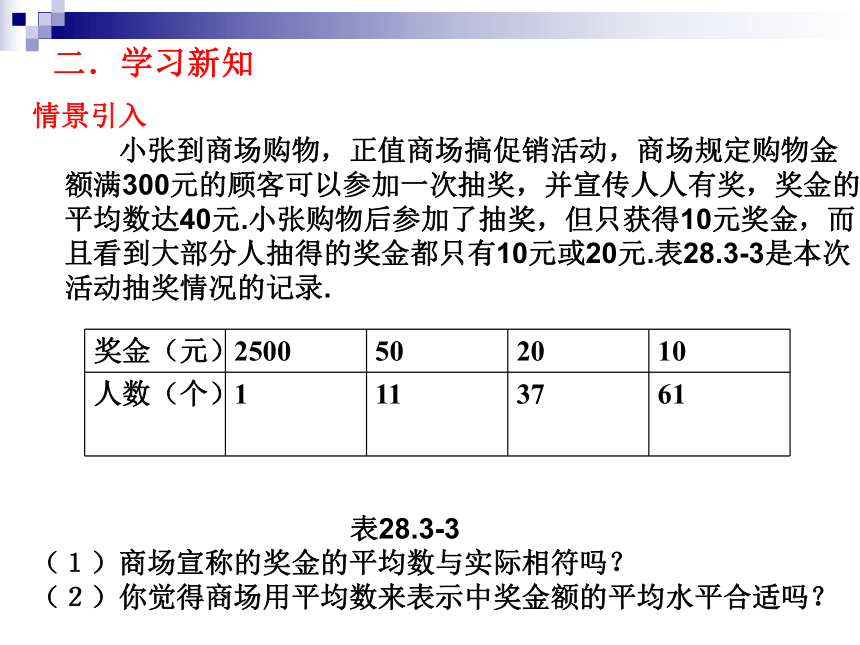
情景引入
小张到商场购物,正值商场搞促销活动,商场规定购物金额满300元的顾客可以参加一次抽奖,并宣传人人有奖,奖金的平均数达40元.小张购物后参加了抽奖,但只获得10元奖金,而且看到大部分人抽得的奖金都只有10元或20元.表28.3-3是本次活动抽奖情况的记录.
表28.3-3
(1)商场宣称的奖金的平均数与实际相符吗?
(2)你觉得商场用平均数来表示中奖金额的平均水平合适吗?
奖金(元)
2500
50
20
10
人数(个)
1
11
37
61
二.学习新知
奖金(元)
2500
50
20
10
人数(个)
1
11
37
61
本例中有98人抽到的奖金只有10元--20元,仅12人抽到的奖金超过40元.平均数失去代表性的原因是2500与其他数据相差太大,对平均数的影响也大,这时用平均数来表示中奖金额的平均水平不合适.
设奖金的平均数为
,用加权平均数的方法
计算,得
可见奖金的平均数的确是40元.
上面的例子表明,当数据中出现极端值时,平均数有时不能很好地反映数据的平均水平.
这种情况用什么反映数据的平均水平呢
概念教学1:
一般地,将 个数据按大小顺序排列,居中的一个数据( 位奇数时),或居中的两个数据( 位偶数时)的平均数,称为这组数据的中位数;出现次数最多的数据称为众数.
即将一组
个数据按大小顺序排列,
当 为奇数时,第
个数据是中位数
当 为偶数时,第
和第
两个数据的平均数是中位数
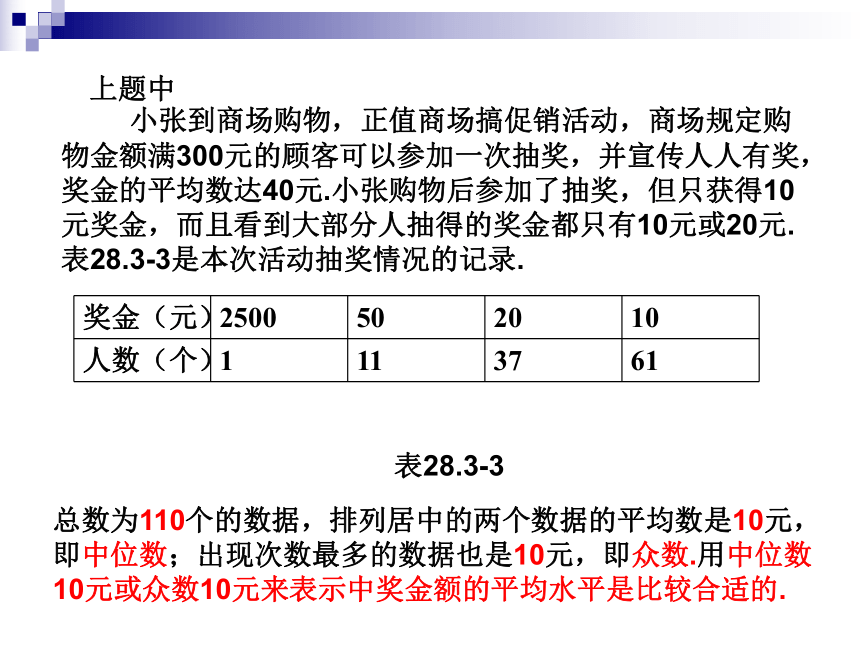
总数为110个的数据,排列居中的两个数据的平均数是10元,即中位数;出现次数最多的数据也是10元,即众数.用中位数10元或众数10元来表示中奖金额的平均水平是比较合适的.
上题中
小张到商场购物,正值商场搞促销活动,商场规定购物金额满300元的顾客可以参加一次抽奖,并宣传人人有奖,奖金的平均数达40元.小张购物后参加了抽奖,但只获得10元奖金,而且看到大部分人抽得的奖金都只有10元或20元.表28.3-3是本次活动抽奖情况的记录.
表28.3-3
奖金(元)
2500
50
20
10
人数(个)
1
11
37
61
三、例题讲解
例题3、某集团公司有9个子公司,各个子公司所创年利润的情况如下表所示.
表28.3--4
根据表中的信息,回答下列问题:
(1)各子公司所创年利润的平均数是多少万元?
(2)各子公司所创年利润的中位数是多少万元?
(3)各子公司所创年利润的众数是多少万元?
(4)你认为应该使用上述哪一个量来表示各子公司所创年利润的平均水平比较合适?
年利润(千万元)
16
4
3
2
子公司个数
1
2
4
2
(2)将9个子公司所创年利润从小到大排列,第5个数据3千万元在中间,所以各子公司所创年利润的中位数是三千万.
(3)看这9个子公司所创年利润数据出现的次数,3千万元出现的次数(4次)最多,所以各子公司所创年利润的众数是3千万元.
(4)由于平均数4.44千万元比8个子公司所创的年利润都高,所以用平均数来表示各子公司所创年利润的平均水平不合适.而中位数及众数都是3千万元,可见用他们来表示各子公司所创年利润的平均水平比较合适.
解:(1)设各子公司所创年利润的平均数
是
,那么
(千万元)
【适时小结】
求一组
个数据的中位数的步骤:
(1)将这组
个数据按大小顺序排列;
(2)确定
是奇数还是偶数;
(3)当
为奇数时,第 个数据是中位数,
当
为偶数时,第 和第 两个数据 的平均数是中位数.
概念教学2:
在实际生活中,还有一种“截尾平均数”.如在一次演唱比赛中,某歌手演唱结束后,七个评委的分数分别是7.5、8.5、8.5、9、9、9.5、9.组委会规定的得分是“去掉一个最高分,去掉一个最低分,取其余5个分数的平均分”.按此规定,去掉7.5和9.5,该歌手的得分是
(分)
这个得分是截尾平均数.
相同点
不同点
都是来描述数据集中趋势的统计量;都可用来反映数据的一般水平.
定义
个数
特点
平均数
一组数据的总和除以这组数据个数所得到的商叫这组数据的平均数
1个
反映了一组数据的平均大小,常用来代表数据的总体
“平均水平”.
中位数
将一组数据按大小顺序排列,处在最中间位置的一个数叫做这组数据的中位数
1个
像一条分界线,将数据分成前半部分和后半部分,因此用来代表一组数据的“中等水平”.
众数
在一组数据中出现次数最多的数叫做这组数据的众数
不确定
反映了出现次数最多的数据,用来代表一组数据的“多数水平”.
【适时小结】
平均数、中位数和众数有哪些共同点和不同点?
例题讲解2:
例题4
某初中中学提倡篮球运动,将投篮命中率作为考察
学生体育成绩的一个项目.为了制定切合本校学生实际的合格标准,
从各年级随机抽取50名学生进行投篮命中次数的测试,
结果如表28.3--5所示.
(1)求测试数据的平均数、中位数和众数;
(2)你认为哪一个表示平均水平的量作为合格标准较为合适?
试简要说明理由.
次数
0
1
2
3
4
5
6
7
8
9
10
人数
1
8
10
7
6
6
5
4
1
2
0
解
(1)设50名学生10次投篮命中次数的平均数为
,则
=
(0
1+1
8+2
10+3
7+4
6+5
6+6
5+7
4+8
1
+9
2+10
0)
=3.74(次).
将50名学生10次投篮命中次数的数据从小到大排列,第
25、26这两个在中间的数据都是3,因此中位数是3次.
众数是2次.
(2)考虑到超过一半以上的学生10次投篮命中次数都在3次以上,因此以中位数3次作为合格标准较为适宜.
四、课堂练习:
1.有人说草地上有六个人在玩,他们的平均年龄为14岁,这时你的脑海里会出现什么情景?
如果告诉你这时一位54岁的大妈领着5个6岁的小朋友在玩,那么与你的想象大致一致吗?应该用平均数、中位数、众数中的那一个数来代表他们的平均年龄更为合适?
2.求下列10数据的平均数、众数和中位数:
0,-1,2,1,0,-2,0,2,-1,0.
3.某商店在一周内卖出某种品牌鞋的尺寸记录如下:
38,42,38,41,40,36,39,40,35,40,43.
商店进货时,应考虑多进的是哪个号码的鞋?这个号 码是平均数、中位数、众数中的哪一个数?
解
1.可能出现的情景是6个青少年在一起玩
;
应该用中位数或众数来代表他们的平均年龄更合适
答:平均数是0.1,中位数和众数都是0.
3.多进40码的鞋,这个号码是众数.
拓展练习:
1.若一组数据6、7、5、6、x、1的平均数是5,则这组数据的
众数是(
)
2.下表是某班20名学生的第一次数学成绩的成绩统计表:
(1)若成绩的平均数为73分,求x和y的值.
(2)设此班20名学生成绩的众数为a,中位数为b,求a-b的值
成绩/分
50
60
70
80
90
人数
1
4
x
y
2
5和6
2.解
(1)由题意得
解得
(2)
五、课堂小结:
本节课你有哪些收获和体会
1.中位数和众数的概念.
2.求一组
个数据的中位数的步骤:
(1)将这组
个数据按大小顺序排列;
(2)确定
是奇数还是偶数;
(3)当
为奇数时,第 个数据是中位数,
当
为偶数时,第 和第 两个数据的平均数是中位数.
六、作业
练习册28.3(2)
§28.3表示一组数据平均水平的量(2)
一.复习引入
提问1:平均数的计算公式是什么
1.一般地,如果一组数据
,
它们的平均数记作
,则
2.若
个数
都在常数
附近波动,那
么
,
,
…
,
记
可得平均数计算公式:
提问2:加权平均数的计算公式是什么?
如果在一组数据
中分别出现次数分别为
,
记
,
,
则
其中
叫做权,
叫做这 个数的加权平均数.
情景引入
小张到商场购物,正值商场搞促销活动,商场规定购物金额满300元的顾客可以参加一次抽奖,并宣传人人有奖,奖金的平均数达40元.小张购物后参加了抽奖,但只获得10元奖金,而且看到大部分人抽得的奖金都只有10元或20元.表28.3-3是本次活动抽奖情况的记录.
表28.3-3
(1)商场宣称的奖金的平均数与实际相符吗?
(2)你觉得商场用平均数来表示中奖金额的平均水平合适吗?
奖金(元)
2500
50
20
10
人数(个)
1
11
37
61
二.学习新知
奖金(元)
2500
50
20
10
人数(个)
1
11
37
61
本例中有98人抽到的奖金只有10元--20元,仅12人抽到的奖金超过40元.平均数失去代表性的原因是2500与其他数据相差太大,对平均数的影响也大,这时用平均数来表示中奖金额的平均水平不合适.
设奖金的平均数为
,用加权平均数的方法
计算,得
可见奖金的平均数的确是40元.
上面的例子表明,当数据中出现极端值时,平均数有时不能很好地反映数据的平均水平.
这种情况用什么反映数据的平均水平呢
概念教学1:
一般地,将 个数据按大小顺序排列,居中的一个数据( 位奇数时),或居中的两个数据( 位偶数时)的平均数,称为这组数据的中位数;出现次数最多的数据称为众数.
即将一组
个数据按大小顺序排列,
当 为奇数时,第
个数据是中位数
当 为偶数时,第
和第
两个数据的平均数是中位数
总数为110个的数据,排列居中的两个数据的平均数是10元,即中位数;出现次数最多的数据也是10元,即众数.用中位数10元或众数10元来表示中奖金额的平均水平是比较合适的.
上题中
小张到商场购物,正值商场搞促销活动,商场规定购物金额满300元的顾客可以参加一次抽奖,并宣传人人有奖,奖金的平均数达40元.小张购物后参加了抽奖,但只获得10元奖金,而且看到大部分人抽得的奖金都只有10元或20元.表28.3-3是本次活动抽奖情况的记录.
表28.3-3
奖金(元)
2500
50
20
10
人数(个)
1
11
37
61
三、例题讲解
例题3、某集团公司有9个子公司,各个子公司所创年利润的情况如下表所示.
表28.3--4
根据表中的信息,回答下列问题:
(1)各子公司所创年利润的平均数是多少万元?
(2)各子公司所创年利润的中位数是多少万元?
(3)各子公司所创年利润的众数是多少万元?
(4)你认为应该使用上述哪一个量来表示各子公司所创年利润的平均水平比较合适?
年利润(千万元)
16
4
3
2
子公司个数
1
2
4
2
(2)将9个子公司所创年利润从小到大排列,第5个数据3千万元在中间,所以各子公司所创年利润的中位数是三千万.
(3)看这9个子公司所创年利润数据出现的次数,3千万元出现的次数(4次)最多,所以各子公司所创年利润的众数是3千万元.
(4)由于平均数4.44千万元比8个子公司所创的年利润都高,所以用平均数来表示各子公司所创年利润的平均水平不合适.而中位数及众数都是3千万元,可见用他们来表示各子公司所创年利润的平均水平比较合适.
解:(1)设各子公司所创年利润的平均数
是
,那么
(千万元)
【适时小结】
求一组
个数据的中位数的步骤:
(1)将这组
个数据按大小顺序排列;
(2)确定
是奇数还是偶数;
(3)当
为奇数时,第 个数据是中位数,
当
为偶数时,第 和第 两个数据 的平均数是中位数.
概念教学2:
在实际生活中,还有一种“截尾平均数”.如在一次演唱比赛中,某歌手演唱结束后,七个评委的分数分别是7.5、8.5、8.5、9、9、9.5、9.组委会规定的得分是“去掉一个最高分,去掉一个最低分,取其余5个分数的平均分”.按此规定,去掉7.5和9.5,该歌手的得分是
(分)
这个得分是截尾平均数.
相同点
不同点
都是来描述数据集中趋势的统计量;都可用来反映数据的一般水平.
定义
个数
特点
平均数
一组数据的总和除以这组数据个数所得到的商叫这组数据的平均数
1个
反映了一组数据的平均大小,常用来代表数据的总体
“平均水平”.
中位数
将一组数据按大小顺序排列,处在最中间位置的一个数叫做这组数据的中位数
1个
像一条分界线,将数据分成前半部分和后半部分,因此用来代表一组数据的“中等水平”.
众数
在一组数据中出现次数最多的数叫做这组数据的众数
不确定
反映了出现次数最多的数据,用来代表一组数据的“多数水平”.
【适时小结】
平均数、中位数和众数有哪些共同点和不同点?
例题讲解2:
例题4
某初中中学提倡篮球运动,将投篮命中率作为考察
学生体育成绩的一个项目.为了制定切合本校学生实际的合格标准,
从各年级随机抽取50名学生进行投篮命中次数的测试,
结果如表28.3--5所示.
(1)求测试数据的平均数、中位数和众数;
(2)你认为哪一个表示平均水平的量作为合格标准较为合适?
试简要说明理由.
次数
0
1
2
3
4
5
6
7
8
9
10
人数
1
8
10
7
6
6
5
4
1
2
0
解
(1)设50名学生10次投篮命中次数的平均数为
,则
=
(0
1+1
8+2
10+3
7+4
6+5
6+6
5+7
4+8
1
+9
2+10
0)
=3.74(次).
将50名学生10次投篮命中次数的数据从小到大排列,第
25、26这两个在中间的数据都是3,因此中位数是3次.
众数是2次.
(2)考虑到超过一半以上的学生10次投篮命中次数都在3次以上,因此以中位数3次作为合格标准较为适宜.
四、课堂练习:
1.有人说草地上有六个人在玩,他们的平均年龄为14岁,这时你的脑海里会出现什么情景?
如果告诉你这时一位54岁的大妈领着5个6岁的小朋友在玩,那么与你的想象大致一致吗?应该用平均数、中位数、众数中的那一个数来代表他们的平均年龄更为合适?
2.求下列10数据的平均数、众数和中位数:
0,-1,2,1,0,-2,0,2,-1,0.
3.某商店在一周内卖出某种品牌鞋的尺寸记录如下:
38,42,38,41,40,36,39,40,35,40,43.
商店进货时,应考虑多进的是哪个号码的鞋?这个号 码是平均数、中位数、众数中的哪一个数?
解
1.可能出现的情景是6个青少年在一起玩
;
应该用中位数或众数来代表他们的平均年龄更合适
答:平均数是0.1,中位数和众数都是0.
3.多进40码的鞋,这个号码是众数.
拓展练习:
1.若一组数据6、7、5、6、x、1的平均数是5,则这组数据的
众数是(
)
2.下表是某班20名学生的第一次数学成绩的成绩统计表:
(1)若成绩的平均数为73分,求x和y的值.
(2)设此班20名学生成绩的众数为a,中位数为b,求a-b的值
成绩/分
50
60
70
80
90
人数
1
4
x
y
2
5和6
2.解
(1)由题意得
解得
(2)
五、课堂小结:
本节课你有哪些收获和体会
1.中位数和众数的概念.
2.求一组
个数据的中位数的步骤:
(1)将这组
个数据按大小顺序排列;
(2)确定
是奇数还是偶数;
(3)当
为奇数时,第 个数据是中位数,
当
为偶数时,第 和第 两个数据的平均数是中位数.
六、作业
练习册28.3(2)
