第一节 圆的基本性质 复习课件(34张PPT)
文档属性
| 名称 | 第一节 圆的基本性质 复习课件(34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 141.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 00:00:00 | ||
图片预览








文档简介
(共34张PPT)
初三数学专题复习
圆的基本性质
基本概念复习
一、定义:
圆是到定点距离等于定长的点的集合。
其中,定点即为此圆的圆心,
定长为此圆的半径。
练习
1
已知:⊙A的半径为3,那么与⊙A相切,且半径为1的圆的圆心O的轨迹是什么?
外切:圆心距d=AO=3+1=4;
内切:圆心距d=AO=3-1=2。
解:当两圆外切时,O的轨迹为以A为圆心,4为半径的圆。
当两圆内切时,O的轨迹为以A为圆心,2为半径的圆。
O
A
.
.
A
O
.
.
示图
二、常用公式
练习2
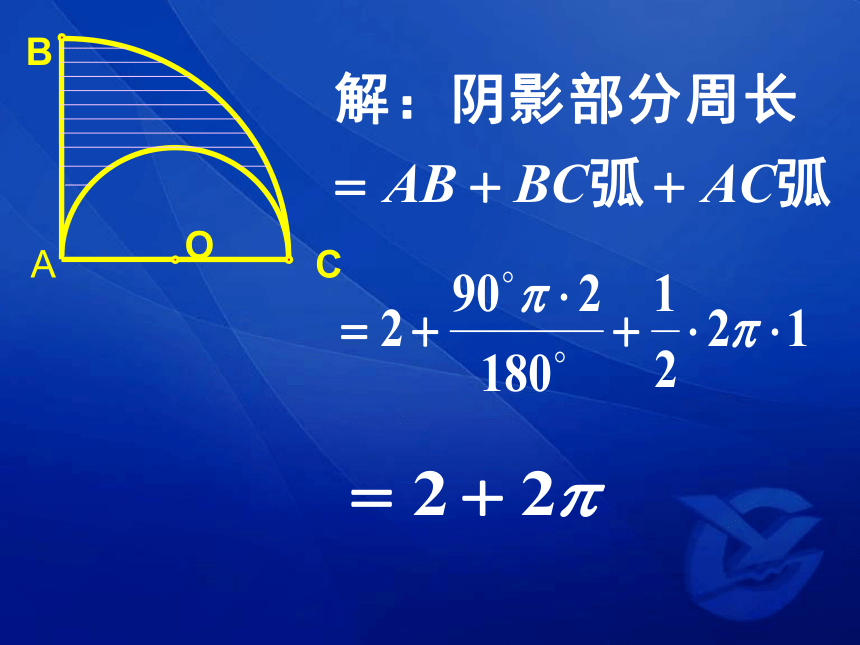
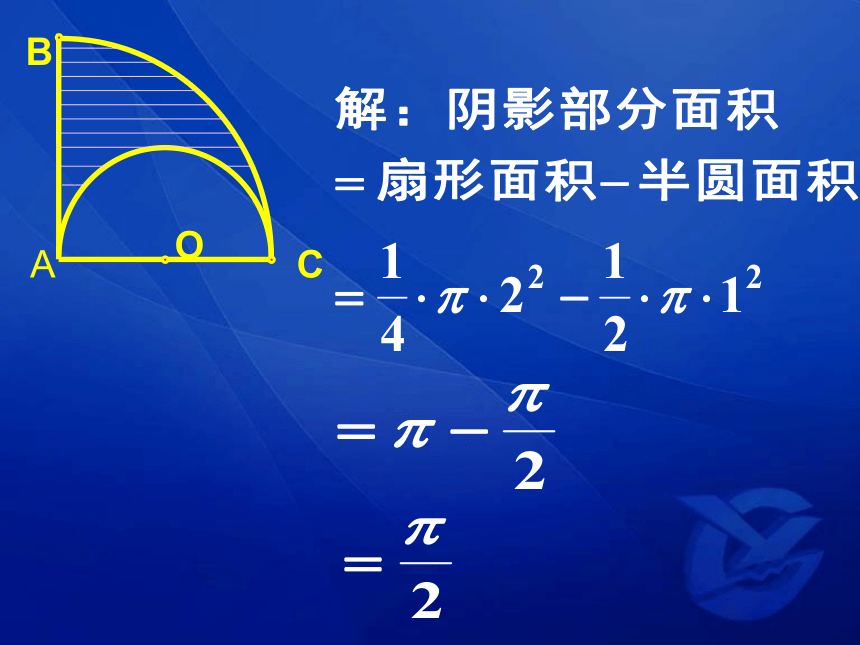
如图,已知,扇形圆心角∠BAC=90。,半径R=2,以AC为直径作半圆O,求阴影部分的周长和面积。
O
A
B
C
O
A
B
C
O
A
B
C
三、常用性质定理
1、同圆或等圆中,各条半径都相等。
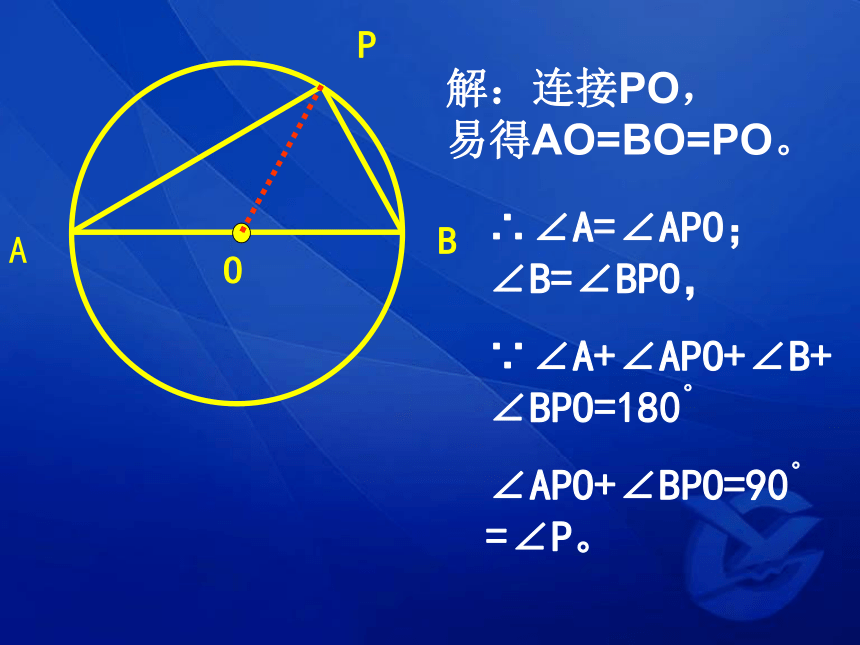
思考:已知点P是以AB为直径的⊙O上一点,则∠P=90。。
A
B
P
O
A
B
P
O
∴∠A=∠APO;∠B=∠BPO,
∵∠A+∠APO+∠B+∠BPO=180。
∠APO+∠BPO=90。=∠P。
解:连接PO,
易得AO=BO=PO。
2、圆是轴对称图形,对称轴为过圆心的直线(直径所在直线),有无数条;圆是中心对称图形,对称中心为圆心。
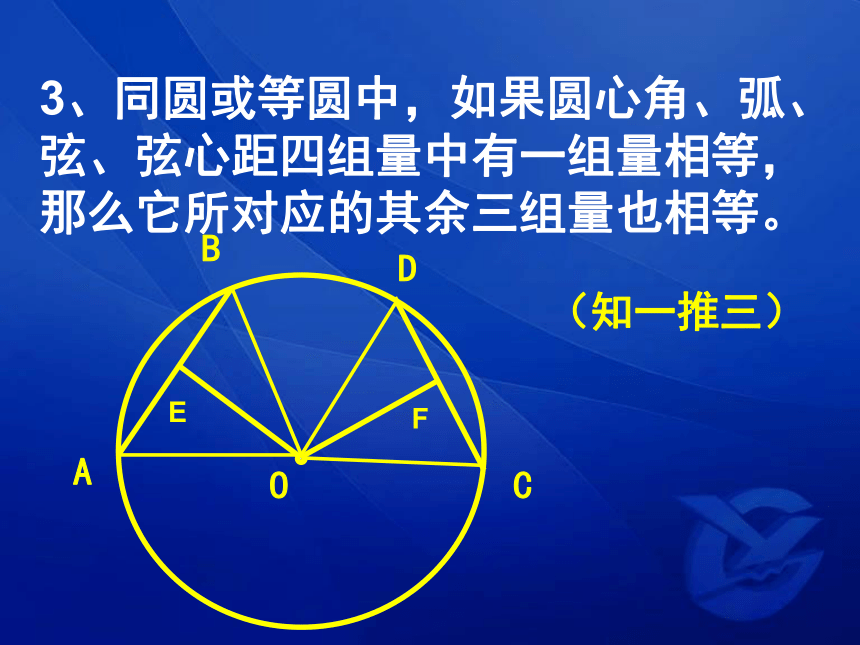
3、同圆或等圆中,如果圆心角、弧、弦、弦心距四组量中有一组量相等,那么它所对应的其余三组量也相等。
O
A
B
C
D
E
F
(知一推三)
4、在一个圆中,垂直于弦的直径平分弦,平分弦所对的弧。
平分弦(此弦非直径)的直径垂直弦且平分弦所对的弧。
弦的垂直平分线过圆心,并且平分弦所对的弧。
练习3
如图,已知⊙O中,直径AB⊥弦CD,垂足为E。请在图中找出相等的线段或角。
O
A
B
C
D
E
O
A
B
C
D
E
或者:
∠COB=∠DOB;
∠OCB=∠OBC=∠OBD=∠ODB;
∠ACO=∠CAO=∠OAD=∠ADO;
∠OCD=∠ODE;
∠ABC=∠ABD等。
由题意可得:
AO=BO=CO=DO;
CE=DE;BC=BD;AC=AD;
辨析:
(1)圆的对称轴是其直径。
(X)
-----直径所在直线
(2)三点确定一个圆。
(X)
-----不共线三点
(3)长度一致的弧是等弧。
(X)
-----所对圆心角的度数也要相同
(4)两弦相等,其所对圆心角也相等。
(X)
-----同圆或等圆中
(5)平分弦的直径垂直此弦。
(X)
-----此弦非直径
(6)三角形的外心一定在三角形外。
(X)
-----只有钝角三角形外心在形外
(8)若一个圆中AB+BC=AC,
则AB+BC=AC。
⌒
⌒
⌒
(X)
-----周长为
A
B
C
(X)
-----AB+BC>AC
巩固练习
已知:⊙O半径OA=1,弦AB、AC分别长
求:∠BAC的大小。
O
A
B
C
E
F
解:作OE⊥AB,OF⊥AC,垂足为E、F。
O
A
B
C
E
F
O
A
B
C
E
F
A
B
O
F
C
E
图1
图2
A
B
O
F
C
E
A
B
C
D
E
O
探索提高:
已知:⊙O中,CD⊥直径AB,CE平分∠DCO交⊙O与E.
求证:AE=BE.
⌒
⌒
A
B
C
D
E
O
证明:连接OE
又∵CE平分∠DCO,
∴∠DCE=OCE=OEC
∴CD∥OE
∵CD⊥AB,∴OE
⊥AB。
即∠AOE=
∠BOE=90。
∴AE=BE。
⌒
⌒
∵CO=EO,∴∠OCE=∠OEC。
A
B
C
D
E
O
思考:若上下平移AB,其余条件不变,原结论是否仍然成立?
A
B
C
D
E
O
证明:连接OE
又∵CE平分∠DCO,
∴∠DCE=OCE=OEC
∴CD∥OE
∵CD⊥AB,∴OE
⊥AB。
∴AE=BE。
即结论不变。
⌒
⌒
∵CO=EO,∴∠OCE=∠OEC。
探索2
如图,已知:⊙0中,AB为直径,直线
L交⊙0于C、D两点。AE、BF分别垂直于L,垂足为E、F。
请找出图中相等的线段,并证明。
A
O
B
C
D
E
F
L
A
O
B
C
D
E
F
L
分析观察得:
1、AO=BO
2、EC=DF
3、ED=FC
H
A
O
B
C
D
E
F
L
证明:
作OH⊥CD,垂足为H。
可得:CH=DH。
又∵AE⊥CD;BF⊥CD,
∴AE∥OH∥BF。
∵AO=BO,
∴EH=FH,
得EH-CH=FH-DH,
即:EC=DF。
A
B
C
D
O
E
F
L
思考:
若旋转AB,使AB与弦CD相交,其余条件不变,上述结论是否有变化?
A
O
B
C
D
E
F
L
A
B
C
D
O
E
F
L
H
证明:
作OH⊥CD,垂足为H。
可得:CH=DH。
又∵AE⊥CD;BF⊥CD,
∴AE∥OH∥BF。
∵AO=BO,
∴EH=FH,
∴
EH-CH
=FH-DH,
即:EC=DF。
A
B
C
D
O
E
F
L
H
A
B
C
D
O
E
F
L
H
课堂小结:
圆作为初中几何学习的一个重要内容,在各个年级数学教学中均有涉及,其重点也在于各知识点的融合。对圆的基本性质的复习可以使同学们加深对圆的理解,并进一步熟悉诸如等腰三角形、直角三角形、垂直平分线、勾股定理、比例线段等一系列基本图形和性质,为圆的深入研究打好基础。
初三数学专题复习
圆的基本性质
基本概念复习
一、定义:
圆是到定点距离等于定长的点的集合。
其中,定点即为此圆的圆心,
定长为此圆的半径。
练习
1
已知:⊙A的半径为3,那么与⊙A相切,且半径为1的圆的圆心O的轨迹是什么?
外切:圆心距d=AO=3+1=4;
内切:圆心距d=AO=3-1=2。
解:当两圆外切时,O的轨迹为以A为圆心,4为半径的圆。
当两圆内切时,O的轨迹为以A为圆心,2为半径的圆。
O
A
.
.
A
O
.
.
示图
二、常用公式
练习2
如图,已知,扇形圆心角∠BAC=90。,半径R=2,以AC为直径作半圆O,求阴影部分的周长和面积。
O
A
B
C
O
A
B
C
O
A
B
C
三、常用性质定理
1、同圆或等圆中,各条半径都相等。
思考:已知点P是以AB为直径的⊙O上一点,则∠P=90。。
A
B
P
O
A
B
P
O
∴∠A=∠APO;∠B=∠BPO,
∵∠A+∠APO+∠B+∠BPO=180。
∠APO+∠BPO=90。=∠P。
解:连接PO,
易得AO=BO=PO。
2、圆是轴对称图形,对称轴为过圆心的直线(直径所在直线),有无数条;圆是中心对称图形,对称中心为圆心。
3、同圆或等圆中,如果圆心角、弧、弦、弦心距四组量中有一组量相等,那么它所对应的其余三组量也相等。
O
A
B
C
D
E
F
(知一推三)
4、在一个圆中,垂直于弦的直径平分弦,平分弦所对的弧。
平分弦(此弦非直径)的直径垂直弦且平分弦所对的弧。
弦的垂直平分线过圆心,并且平分弦所对的弧。
练习3
如图,已知⊙O中,直径AB⊥弦CD,垂足为E。请在图中找出相等的线段或角。
O
A
B
C
D
E
O
A
B
C
D
E
或者:
∠COB=∠DOB;
∠OCB=∠OBC=∠OBD=∠ODB;
∠ACO=∠CAO=∠OAD=∠ADO;
∠OCD=∠ODE;
∠ABC=∠ABD等。
由题意可得:
AO=BO=CO=DO;
CE=DE;BC=BD;AC=AD;
辨析:
(1)圆的对称轴是其直径。
(X)
-----直径所在直线
(2)三点确定一个圆。
(X)
-----不共线三点
(3)长度一致的弧是等弧。
(X)
-----所对圆心角的度数也要相同
(4)两弦相等,其所对圆心角也相等。
(X)
-----同圆或等圆中
(5)平分弦的直径垂直此弦。
(X)
-----此弦非直径
(6)三角形的外心一定在三角形外。
(X)
-----只有钝角三角形外心在形外
(8)若一个圆中AB+BC=AC,
则AB+BC=AC。
⌒
⌒
⌒
(X)
-----周长为
A
B
C
(X)
-----AB+BC>AC
巩固练习
已知:⊙O半径OA=1,弦AB、AC分别长
求:∠BAC的大小。
O
A
B
C
E
F
解:作OE⊥AB,OF⊥AC,垂足为E、F。
O
A
B
C
E
F
O
A
B
C
E
F
A
B
O
F
C
E
图1
图2
A
B
O
F
C
E
A
B
C
D
E
O
探索提高:
已知:⊙O中,CD⊥直径AB,CE平分∠DCO交⊙O与E.
求证:AE=BE.
⌒
⌒
A
B
C
D
E
O
证明:连接OE
又∵CE平分∠DCO,
∴∠DCE=OCE=OEC
∴CD∥OE
∵CD⊥AB,∴OE
⊥AB。
即∠AOE=
∠BOE=90。
∴AE=BE。
⌒
⌒
∵CO=EO,∴∠OCE=∠OEC。
A
B
C
D
E
O
思考:若上下平移AB,其余条件不变,原结论是否仍然成立?
A
B
C
D
E
O
证明:连接OE
又∵CE平分∠DCO,
∴∠DCE=OCE=OEC
∴CD∥OE
∵CD⊥AB,∴OE
⊥AB。
∴AE=BE。
即结论不变。
⌒
⌒
∵CO=EO,∴∠OCE=∠OEC。
探索2
如图,已知:⊙0中,AB为直径,直线
L交⊙0于C、D两点。AE、BF分别垂直于L,垂足为E、F。
请找出图中相等的线段,并证明。
A
O
B
C
D
E
F
L
A
O
B
C
D
E
F
L
分析观察得:
1、AO=BO
2、EC=DF
3、ED=FC
H
A
O
B
C
D
E
F
L
证明:
作OH⊥CD,垂足为H。
可得:CH=DH。
又∵AE⊥CD;BF⊥CD,
∴AE∥OH∥BF。
∵AO=BO,
∴EH=FH,
得EH-CH=FH-DH,
即:EC=DF。
A
B
C
D
O
E
F
L
思考:
若旋转AB,使AB与弦CD相交,其余条件不变,上述结论是否有变化?
A
O
B
C
D
E
F
L
A
B
C
D
O
E
F
L
H
证明:
作OH⊥CD,垂足为H。
可得:CH=DH。
又∵AE⊥CD;BF⊥CD,
∴AE∥OH∥BF。
∵AO=BO,
∴EH=FH,
∴
EH-CH
=FH-DH,
即:EC=DF。
A
B
C
D
O
E
F
L
H
A
B
C
D
O
E
F
L
H
课堂小结:
圆作为初中几何学习的一个重要内容,在各个年级数学教学中均有涉及,其重点也在于各知识点的融合。对圆的基本性质的复习可以使同学们加深对圆的理解,并进一步熟悉诸如等腰三角形、直角三角形、垂直平分线、勾股定理、比例线段等一系列基本图形和性质,为圆的深入研究打好基础。
