27.1 圆的确定 课件(17张PPT)
文档属性
| 名称 | 27.1 圆的确定 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 142.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 11:24:12 | ||
图片预览





文档简介
(共17张PPT)
27.1
圆的确定
复习引入
圆是怎样定义的?
什么是圆心和圆的半径?
确定圆的要素是什么?
圆是平面上到定点的距离等于定长的所有点所成的图形
这个定点是圆心,联结圆心和圆上任意一点的线段是圆的半径
以点O为圆心的圆称为圆O,记作⊙O.
圆心决定圆的位置,半径决定圆的大小
回顾:(1)过平面上一点,能做多少条直线?
(2)几个点可以确定一条直线?
过几个点可以确定一个圆呢?
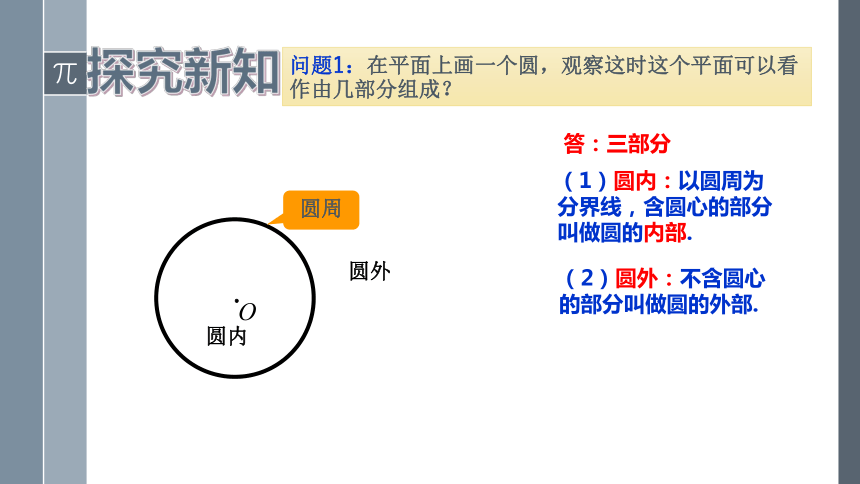
问题1:在平面上画一个圆,观察这时这个平面可以看作由几部分组成?
·
O
圆内
圆外
圆周
答:三部分
(1)圆内:以圆周为
分界线,含圆心的部分
叫做圆的内部.
(2)圆外:不含圆心
的部分叫做圆的外部.
探究新知
M
·
·
·
·
O
A
B
C
问题2:(1)观察图中点A,点B,点C与圆O的位置关系如何?
(2)设⊙O半径为r,说出点A,点B,点C到圆心O的距离与半径的数量关系
r
探究新知
(3)若已知点到圆心的距离和圆的半径
,能否判断点和圆的位置关系
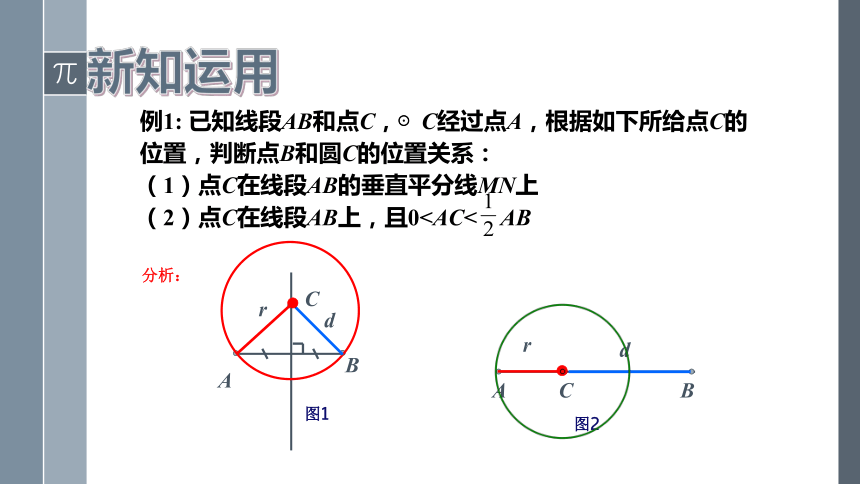
例1:
已知线段AB和点C,⊙C经过点A,根据如下所给点C的
位置,判断点B和圆C的位置关系:
(1)点C在线段AB的垂直平分线MN上
(2)点C在线段AB上,且0AB
A
C
B
C
A
B
图1
图2
r
分析:
d
r
d
新知运用
例题1
已知线段AB和点C,⊙C经过点A,根据如下所给点C的位置,判断点B与⊙C的位置关系。
(1)点C在线段AB的垂直平分线上
解
∵⊙C经过点A,
∴CA是⊙C的半径。
∵点C在线段AB的垂直平分线上
∴CB=CA
∴点B在⊙C上。
(2)点C在线段AB上,且0AB
∵点C在线段AB上,
∴AC+BC=AB,
又∵AC<
AB。
∴BC>
AB。
得BC>AC。
∵AC是⊙C的半径,
∴点B在⊙C外。
A
C
B
图1
r
d
C
A
B
图2
r
d
·
·
·
·
·
·
A
B
A
问题2:如图作经过已知点A、B的圆,这样的圆你能作出多少个?这些圆的圆心分布有什么特点?
问题1:经过一点A作圆,能作多少个?
这些圆的圆心都在线段AB的垂直平分线上.
探究新知
猜想:经过平面上的三点是否能确定一个圆?
探究新知
定理:不在同一条直线上的三个点确定一个圆.
外接圆的圆心叫做这个三角形的外心.
三角形的外心是三边中垂线的交点.
C
O
A
B
经过三角形的三个顶点可以做一个圆,这个圆叫做三角形的外接圆
这个三角形叫做这个圆的内接三角形.
如图,⊙O是△ABC的外接圆,△ABC是⊙O的内接三角形
概念学习
A
B
C
D
如果一个圆经过一个多边形的各顶点,
那么这个圆叫做这个多边形的外接圆.
这个多边形叫做这个圆的内接多边形.
如图,⊙O是四边形ABCD的外接圆,
四边形ABCD是⊙O的内接四边形.
概念学习
小组合作:用直尺和圆规作出下列三角形的外接圆
新知运用
锐角三角形的外心位于三角形内,直角三角形的外心位于直角三角形斜边中点,钝角三角形的外心位于三角形外.
1.多选:选出下列命题中假命题(
)
(1)经过三点一定可以作圆.
(2)三角形的外心就是这个三角形两边垂
直平分线的交点。
(3)三角形的外心到三边的距离相等。
(4)任意一个三角形一定有一个外接圆,并
且只有一个外接圆.
(5)任意一个圆一定有一个内接三角形,并且
只有一个内接三角形.
不共线三点
×
√
×
三个顶点
√
×
无数个
课堂练习
A
B
C
D
2.经过不在同一直线上的任意四点,是否一定
可以作一个圆?举例说明.
不一定
A
B
C
D
A
B
C
D
A
B
C
D
课堂练习
课堂小结
谈谈你的收获
4.已知平面直角坐标系内点A的坐标为(3,0),A为圆心,AO
为半径作圆.
(1)判断点B(4,2),C(1,4)与圆A的位置关系;
(2)已知点D的纵坐标为2,且点D在
上,求点D的坐标.
拓展练习
27.1
圆的确定
复习引入
圆是怎样定义的?
什么是圆心和圆的半径?
确定圆的要素是什么?
圆是平面上到定点的距离等于定长的所有点所成的图形
这个定点是圆心,联结圆心和圆上任意一点的线段是圆的半径
以点O为圆心的圆称为圆O,记作⊙O.
圆心决定圆的位置,半径决定圆的大小
回顾:(1)过平面上一点,能做多少条直线?
(2)几个点可以确定一条直线?
过几个点可以确定一个圆呢?
问题1:在平面上画一个圆,观察这时这个平面可以看作由几部分组成?
·
O
圆内
圆外
圆周
答:三部分
(1)圆内:以圆周为
分界线,含圆心的部分
叫做圆的内部.
(2)圆外:不含圆心
的部分叫做圆的外部.
探究新知
M
·
·
·
·
O
A
B
C
问题2:(1)观察图中点A,点B,点C与圆O的位置关系如何?
(2)设⊙O半径为r,说出点A,点B,点C到圆心O的距离与半径的数量关系
r
探究新知
(3)若已知点到圆心的距离和圆的半径
,能否判断点和圆的位置关系
例1:
已知线段AB和点C,⊙C经过点A,根据如下所给点C的
位置,判断点B和圆C的位置关系:
(1)点C在线段AB的垂直平分线MN上
(2)点C在线段AB上,且0
A
C
B
C
A
B
图1
图2
r
分析:
d
r
d
新知运用
例题1
已知线段AB和点C,⊙C经过点A,根据如下所给点C的位置,判断点B与⊙C的位置关系。
(1)点C在线段AB的垂直平分线上
解
∵⊙C经过点A,
∴CA是⊙C的半径。
∵点C在线段AB的垂直平分线上
∴CB=CA
∴点B在⊙C上。
(2)点C在线段AB上,且0
∵点C在线段AB上,
∴AC+BC=AB,
又∵AC<
AB。
∴BC>
AB。
得BC>AC。
∵AC是⊙C的半径,
∴点B在⊙C外。
A
C
B
图1
r
d
C
A
B
图2
r
d
·
·
·
·
·
·
A
B
A
问题2:如图作经过已知点A、B的圆,这样的圆你能作出多少个?这些圆的圆心分布有什么特点?
问题1:经过一点A作圆,能作多少个?
这些圆的圆心都在线段AB的垂直平分线上.
探究新知
猜想:经过平面上的三点是否能确定一个圆?
探究新知
定理:不在同一条直线上的三个点确定一个圆.
外接圆的圆心叫做这个三角形的外心.
三角形的外心是三边中垂线的交点.
C
O
A
B
经过三角形的三个顶点可以做一个圆,这个圆叫做三角形的外接圆
这个三角形叫做这个圆的内接三角形.
如图,⊙O是△ABC的外接圆,△ABC是⊙O的内接三角形
概念学习
A
B
C
D
如果一个圆经过一个多边形的各顶点,
那么这个圆叫做这个多边形的外接圆.
这个多边形叫做这个圆的内接多边形.
如图,⊙O是四边形ABCD的外接圆,
四边形ABCD是⊙O的内接四边形.
概念学习
小组合作:用直尺和圆规作出下列三角形的外接圆
新知运用
锐角三角形的外心位于三角形内,直角三角形的外心位于直角三角形斜边中点,钝角三角形的外心位于三角形外.
1.多选:选出下列命题中假命题(
)
(1)经过三点一定可以作圆.
(2)三角形的外心就是这个三角形两边垂
直平分线的交点。
(3)三角形的外心到三边的距离相等。
(4)任意一个三角形一定有一个外接圆,并
且只有一个外接圆.
(5)任意一个圆一定有一个内接三角形,并且
只有一个内接三角形.
不共线三点
×
√
×
三个顶点
√
×
无数个
课堂练习
A
B
C
D
2.经过不在同一直线上的任意四点,是否一定
可以作一个圆?举例说明.
不一定
A
B
C
D
A
B
C
D
A
B
C
D
课堂练习
课堂小结
谈谈你的收获
4.已知平面直角坐标系内点A的坐标为(3,0),A为圆心,AO
为半径作圆.
(1)判断点B(4,2),C(1,4)与圆A的位置关系;
(2)已知点D的纵坐标为2,且点D在
上,求点D的坐标.
拓展练习
