27.1 圆的确定 课件(21张PPT)
文档属性
| 名称 | 27.1 圆的确定 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 757.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 11:13:26 | ||
图片预览







文档简介
(共21张PPT)
观察下列生活中常见的物体,它们都给我们以
什么形象?
圆是平面上到一个定点的距离等于定长的所有点所成的图形。
圆的概念:
确定圆的条件:
(1)圆心
:确定圆的位置
(2)半径
:确定圆的大小
以点O为圆心的圆称为圆O,记作⊙O
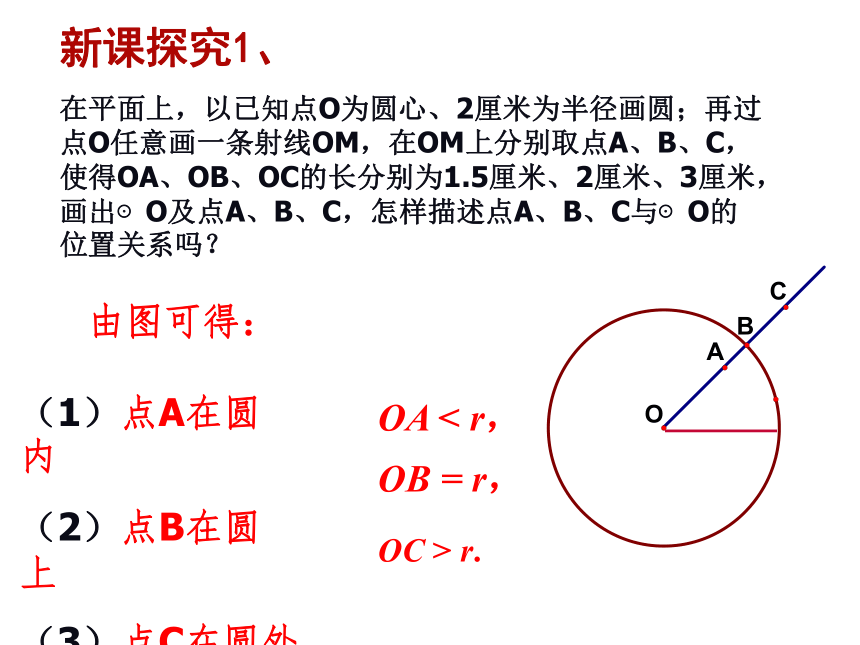
在平面上,以已知点O为圆心、2厘米为半径画圆;再过点O任意画一条射线OM,在OM上分别取点A、B、C,使得OA、OB、OC的长分别为1.5厘米、2厘米、3厘米,画出⊙O及点A、B、C,怎样描述点A、B、C与⊙O的位置关系吗?
新课探究1、
(1)点A在圆内
(2)点B在圆上
(3)点C在圆外
由图可得:
OA
<
r,
OB
=
r,
OC
>
r.
设⊙O的半径为r,点P到圆心的距离OP
=
d,则点P与⊙O的位置与r、
d关系:
r
·
O
A
P
P
P
(1)点在圆外(2)点在圆上
(3)点在圆内
平面上的圆可以将平面分成三部分
(1)圆的内部(2)圆周
(3)圆的外部
圆内
圆外
圆周
圆的内部:
可以看作到圆心的距离小于
半径的点的集合(包含圆心)
圆的外部:
可以看作到圆心的距离大于
半径的点的集合。
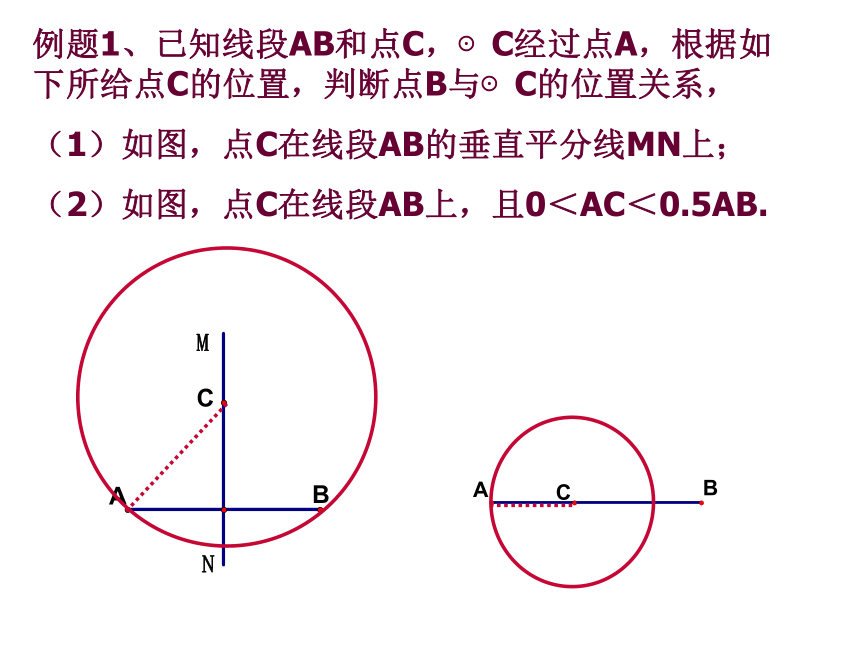
例题1、已知线段AB和点C,⊙C经过点A,根据如下所给点C的位置,判断点B与⊙C的位置关系,
(1)如图,点C在线段AB的垂直平分线MN上;
(2)如图,点C在线段AB上,且0<AC<0.5AB.
由例题1(1)可知,如果圆心C在线段AB的垂直平分线上,那么以CA为半径的圆C一定经过A、B两点。反之,如果圆C经过A、B两点,那么圆心C一定在线段AB的垂直平分线上吗?
这样的圆可以作多少个?
·
·
·
A
B
在平面上,经过给定三点的圆是否
仍然“有无数个”?圆心的位置又如何?
B
C
A
1、当三点不在一直线上时:
O
A
B
C
2、当三点在一直线上时:
定理:
不在一直线上的三个点确定一个圆。
(经过三角形的三个顶点可以确定一个圆)
B
C
A
概念:
1、经过三角形各顶点的圆叫三角形
的外接圆。
这个三角形叫做圆的内接三角形。
2、三角形外接圆的圆心叫做三角形的外心。
它是三角形三边的垂直平分线的交点。
画一画
试一试、已知三角形ABC,用直尺与圆规作出下面三角形的外接圆,并观察圆心的位置有怎样的特点。
B
C
A
三角形外接圆的作图步骤:
三角形的外心位置:
1、锐角三角形的外心在三角形的内部。
2、直角三角形的外心在斜边的中点。
3、钝角三角形的外心在三角形的外部。
四边形有外接圆吗?
3:如图如果一个圆经过多边形的各个顶点,那么
这个圆叫做多边形的外接圆。这个多边形叫做圆
的内接多边形。
1、已知一个圆的圆心在坐标原点,半径为5,试判断点A(3,6)、B(-3,4)
、
C(-1,2)
与圆O的位置关系。
三、练习反馈
2、有一圆盘,不慎打碎了,仅留下如图较为完整得一块,你能确定这个碎圆盘所在得圆得圆心吗?用今天学得知识说明理由。
∴点O就是所求得圆心
3、已知△DEF的外心在△DEF的一边上,
若DE=3,EF=4,能否求出△DEF的
外接圆半径?
小结:
回忆一下
交流一下
反思一下
观察下列生活中常见的物体,它们都给我们以
什么形象?
圆是平面上到一个定点的距离等于定长的所有点所成的图形。
圆的概念:
确定圆的条件:
(1)圆心
:确定圆的位置
(2)半径
:确定圆的大小
以点O为圆心的圆称为圆O,记作⊙O
在平面上,以已知点O为圆心、2厘米为半径画圆;再过点O任意画一条射线OM,在OM上分别取点A、B、C,使得OA、OB、OC的长分别为1.5厘米、2厘米、3厘米,画出⊙O及点A、B、C,怎样描述点A、B、C与⊙O的位置关系吗?
新课探究1、
(1)点A在圆内
(2)点B在圆上
(3)点C在圆外
由图可得:
OA
<
r,
OB
=
r,
OC
>
r.
设⊙O的半径为r,点P到圆心的距离OP
=
d,则点P与⊙O的位置与r、
d关系:
r
·
O
A
P
P
P
(1)点在圆外(2)点在圆上
(3)点在圆内
平面上的圆可以将平面分成三部分
(1)圆的内部(2)圆周
(3)圆的外部
圆内
圆外
圆周
圆的内部:
可以看作到圆心的距离小于
半径的点的集合(包含圆心)
圆的外部:
可以看作到圆心的距离大于
半径的点的集合。
例题1、已知线段AB和点C,⊙C经过点A,根据如下所给点C的位置,判断点B与⊙C的位置关系,
(1)如图,点C在线段AB的垂直平分线MN上;
(2)如图,点C在线段AB上,且0<AC<0.5AB.
由例题1(1)可知,如果圆心C在线段AB的垂直平分线上,那么以CA为半径的圆C一定经过A、B两点。反之,如果圆C经过A、B两点,那么圆心C一定在线段AB的垂直平分线上吗?
这样的圆可以作多少个?
·
·
·
A
B
在平面上,经过给定三点的圆是否
仍然“有无数个”?圆心的位置又如何?
B
C
A
1、当三点不在一直线上时:
O
A
B
C
2、当三点在一直线上时:
定理:
不在一直线上的三个点确定一个圆。
(经过三角形的三个顶点可以确定一个圆)
B
C
A
概念:
1、经过三角形各顶点的圆叫三角形
的外接圆。
这个三角形叫做圆的内接三角形。
2、三角形外接圆的圆心叫做三角形的外心。
它是三角形三边的垂直平分线的交点。
画一画
试一试、已知三角形ABC,用直尺与圆规作出下面三角形的外接圆,并观察圆心的位置有怎样的特点。
B
C
A
三角形外接圆的作图步骤:
三角形的外心位置:
1、锐角三角形的外心在三角形的内部。
2、直角三角形的外心在斜边的中点。
3、钝角三角形的外心在三角形的外部。
四边形有外接圆吗?
3:如图如果一个圆经过多边形的各个顶点,那么
这个圆叫做多边形的外接圆。这个多边形叫做圆
的内接多边形。
1、已知一个圆的圆心在坐标原点,半径为5,试判断点A(3,6)、B(-3,4)
、
C(-1,2)
与圆O的位置关系。
三、练习反馈
2、有一圆盘,不慎打碎了,仅留下如图较为完整得一块,你能确定这个碎圆盘所在得圆得圆心吗?用今天学得知识说明理由。
∴点O就是所求得圆心
3、已知△DEF的外心在△DEF的一边上,
若DE=3,EF=4,能否求出△DEF的
外接圆半径?
小结:
回忆一下
交流一下
反思一下
