28.3(2) 中位数、众数、截尾平均数 课件(18张PPT)
文档属性
| 名称 | 28.3(2) 中位数、众数、截尾平均数 课件(18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 11:24:12 | ||
图片预览






文档简介
(共18张PPT)
招工启事
本单位需要招聘研究员一人,
有意者请来单位面试。
体育科研室人事部
2018年5月5日
这个单位员工收入到底怎样?
我这里报酬不错,
月平均工资是4000元,你在这里好好干!
人事主任
应聘者小王
第二天,小王上班了。
研究员F
我的工资是3500元,在单位算中等收入
研究员D
我们好几个人工资都是3200元
人事主任
应聘者小王
小王在单位工作了一周后
你欺骗了我,我已问过其他研究员,没有一个研究员的工资超过4000元.
平均工资是每月4000元,你看看单位的工资报表.
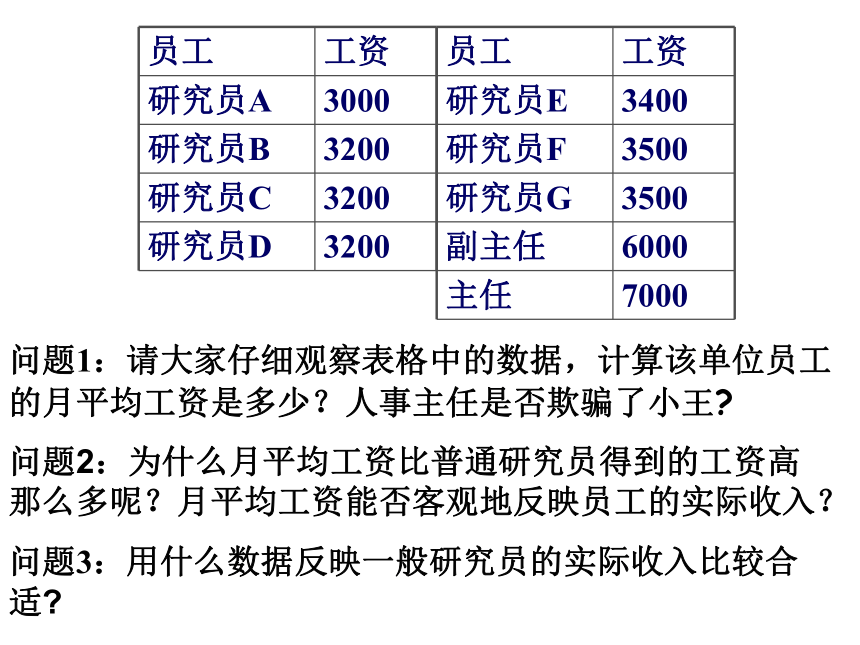
问题1:请大家仔细观察表格中的数据,计算该单位员工的月平均工资是多少?人事主任是否欺骗了小王
问题3:用什么数据反映一般研究员的实际收入比较合适
问题2:为什么月平均工资比普通研究员得到的工资高那么多呢?月平均工资能否客观地反映员工的实际收入?
员工
工资
研究员A
3000
研究员B
3200
研究员C
3200
研究员D
3200
员工
工资
研究员E
3400
研究员F
3500
研究员G
3500
副主任
6000
主任
7000
中位数:将n个数据按大小依次排列,居中的一个数据叫做这组数据的中位数。
众数:在一组数据中,出现次数最多的数据叫做这组数据的众数。
众数
实习生
研究员A
研究员B
研究员C
研究员D
研究员E
研究员F
研究员G
副主任
主任
2000
3000
3200
3200
3200
3400
3500
3500
6000
7000
中位数
中位数:将n个数据按大小依次排列,当n为奇数时,居中的一个数据,称为这组数据的中位数;当n为偶数时,居中两个数据的平均数,称为这组数据的中位数。
当n为奇数时,中位数是第
个数据
当n为偶数时,中位数是第
个和第
个数据的平均数.
1、如何确定一组数据的中位数
第1步:排序,由小到大或由大到小.
第2步:看数据的个数是奇数还是偶数.
注意:中位数是一个数据而非这个数据的序数
4
5
6
7
8
4
5
6
7
8
9
10
4
5
6
7
8
9
10
11
12
4
5
6
3
4
5
6
7
8
3
4
5
6
7
8
9
10
5个数据→第3个中位数
7个数据→第4个中位数
9个数据→第5个中位数
4个数据→第2、3个平均数
6个数据→第3、4个平均数
8个数据→第4、5个平均数
2、众数:
如果有两个或两个以上个数出现次数都是最多的,那么这几个数都是这组数据的众数.例如:1,2,2,3,3,4的众数是
。
2和3
注意:众数是数据而非这个数据出现的次数。
1、数据10,4,
5,
2,4的中位数是(
)
A.4
B.10
C.2
D.5
2、数据10,8,4,6,2,7的中位数是
(
)
A.6
B.10
C.6.5
D.7
4、数据10,20,30,20,30,40的众数是(
)
A.2
B.
20和30
C.30
D.20
A
C
C
3、数据1、2、2、2、3、5的众数是(
)
A.4
B.3
C.2
D.5
B
2
4
4
5
10
2
4
6
7
8
10
在实际生活中,还有一种“截尾平均数”
如在跳水比赛中,某跳水运动员动作完成后,七个裁判评定的分数分别为7.5、8.5、8.5、9、9、9.5、9。
按组委会规定
“去掉一个最高分,去掉一个最低分,取剩下5个分数的平均分”。
按此规定,该运动员得分是:
这个平均数是叫做截尾平均数。
去掉7.5和9.5,
例1:某班9位同学参加一分钟跳短绳测试项目,成绩分别为(个/每分钟)
98,91,100,93,103,167,105,91,115
(1)这组数据的平均数是一分钟多少个?
(2)这组数据的中位数是一分钟多少个?
(3)这组数据的众数是一分钟多少个?
(4)你认为应该使用上述哪一个量来表示班级跳绳的平均水平比较合适?
上海国际半程马拉松赛于4月22日在上海东方明珠塔下开跑。15000名跑者踏上充满活力与美丽的赛道,经南浦大桥、世博大道、前滩公园,奔向终点东方体育中心。
半程马拉松:二分之一马拉松,目前国际上从众增长最快的赛跑项目。路程长度是21.0975公里,或13.1英里。因为半程马拉松的程长很有挑战性,但对跑步者的要求又不像全程马拉松那么严苛。
马拉松:国际上非常普及的长跑比赛项目,全程距离26英里385码,折合为42.195公里。分全程马拉松、半程马拉松和四分马拉松三种。
半程马拉松的最好成绩:
男子:厄立特里亚选手Zersenay
Tadese于2010年3月21日在葡萄牙里斯本创造的58:23。
女子:肯尼亚选手乔塞琳·杰普科西盖于2017年4月1日在布拉格创造的1:04:52。
练习1:在半程马拉松比赛中,获得其中12名选手的成绩如下(单位:分)
85 90 79 130
74
104
95
96
108
126 115 98
(1)样本数据(12名选手的成绩)的平均数是多少?
(2)样本数据(12名选手的成绩)的中位数是多少?
(3)一名选手的成绩是92分,他的成绩如何?
由(1)中样本数据的结论可以估计,在这次马拉松比赛的总体成绩中,约有一半的选手的成绩慢于97分,约有一半的选手的成绩快于97分,故成绩为92分钟的选手比一半以上选手的成绩要好。
(1)平均数:100
(2)中位数:97
不同点:
计算平均数时,所有数据都参加运算,它能充分利用所有数据提供的信息,但容易受极端值的影响。它应用最为广泛。
中位数的优点是计算简单,不受极端值的影响,只与其在数据中的位置有关。但不能充分利用所有的数据信息。一组数据的中位数是唯一的。
众数不受极端值的影响,只与其在数据中重复的次数有关,而且往往不是唯一的。
但不能充分利用所有的数据信息,而且当各个数据的重复次数大致相等时,众数往往没有特别的意义。
平均数、中位数和众数有哪些共同点和不同点?
共同点:都反映一组数据的平均水平,它们是表示一组数据平均水平的量。
例2:
某中学对40名男同学所穿运动鞋的尺码进行调查,
调查结果如下表:
尺码
37
38
39
40
41
42
人数
2
8
8
19
2
1
学校商店进货时,应该考虑多进哪种尺码的男式运动鞋?这个号码是平均数、中位数、众数中的哪一个数?
练习2:某初级中学提倡篮球运动,将投篮命中率作为考查学生体育成绩的一个项目,为了制定切合本校学生实际合格的标准,从各年级随机抽取50名学生进行10次投篮命中次数的测验,结果如图所示:
次数
0
1
2
3
4
5
6
7
8
9
10
人数
1
8
10
7
6
6
5
4
1
2
0
(1)求测试数据的平均数、中位数和众数。
(2)你认为哪一个表示平均水平的量作为标准较为合适?试简要说明理由。
(1)平均数:3.74
中位数:3
众数:2
中位数:将n个数据按大小依次排列,当n为奇数时,居中的一个数据,称为这组数据的中位数;当n为偶数时,居中两个数据的平均数,称为这组数据的中位数。
众数:在一组数据中,出现次数最多的数据叫做这组数据的众数。
招工启事
本单位需要招聘研究员一人,
有意者请来单位面试。
体育科研室人事部
2018年5月5日
这个单位员工收入到底怎样?
我这里报酬不错,
月平均工资是4000元,你在这里好好干!
人事主任
应聘者小王
第二天,小王上班了。
研究员F
我的工资是3500元,在单位算中等收入
研究员D
我们好几个人工资都是3200元
人事主任
应聘者小王
小王在单位工作了一周后
你欺骗了我,我已问过其他研究员,没有一个研究员的工资超过4000元.
平均工资是每月4000元,你看看单位的工资报表.
问题1:请大家仔细观察表格中的数据,计算该单位员工的月平均工资是多少?人事主任是否欺骗了小王
问题3:用什么数据反映一般研究员的实际收入比较合适
问题2:为什么月平均工资比普通研究员得到的工资高那么多呢?月平均工资能否客观地反映员工的实际收入?
员工
工资
研究员A
3000
研究员B
3200
研究员C
3200
研究员D
3200
员工
工资
研究员E
3400
研究员F
3500
研究员G
3500
副主任
6000
主任
7000
中位数:将n个数据按大小依次排列,居中的一个数据叫做这组数据的中位数。
众数:在一组数据中,出现次数最多的数据叫做这组数据的众数。
众数
实习生
研究员A
研究员B
研究员C
研究员D
研究员E
研究员F
研究员G
副主任
主任
2000
3000
3200
3200
3200
3400
3500
3500
6000
7000
中位数
中位数:将n个数据按大小依次排列,当n为奇数时,居中的一个数据,称为这组数据的中位数;当n为偶数时,居中两个数据的平均数,称为这组数据的中位数。
当n为奇数时,中位数是第
个数据
当n为偶数时,中位数是第
个和第
个数据的平均数.
1、如何确定一组数据的中位数
第1步:排序,由小到大或由大到小.
第2步:看数据的个数是奇数还是偶数.
注意:中位数是一个数据而非这个数据的序数
4
5
6
7
8
4
5
6
7
8
9
10
4
5
6
7
8
9
10
11
12
4
5
6
3
4
5
6
7
8
3
4
5
6
7
8
9
10
5个数据→第3个中位数
7个数据→第4个中位数
9个数据→第5个中位数
4个数据→第2、3个平均数
6个数据→第3、4个平均数
8个数据→第4、5个平均数
2、众数:
如果有两个或两个以上个数出现次数都是最多的,那么这几个数都是这组数据的众数.例如:1,2,2,3,3,4的众数是
。
2和3
注意:众数是数据而非这个数据出现的次数。
1、数据10,4,
5,
2,4的中位数是(
)
A.4
B.10
C.2
D.5
2、数据10,8,4,6,2,7的中位数是
(
)
A.6
B.10
C.6.5
D.7
4、数据10,20,30,20,30,40的众数是(
)
A.2
B.
20和30
C.30
D.20
A
C
C
3、数据1、2、2、2、3、5的众数是(
)
A.4
B.3
C.2
D.5
B
2
4
4
5
10
2
4
6
7
8
10
在实际生活中,还有一种“截尾平均数”
如在跳水比赛中,某跳水运动员动作完成后,七个裁判评定的分数分别为7.5、8.5、8.5、9、9、9.5、9。
按组委会规定
“去掉一个最高分,去掉一个最低分,取剩下5个分数的平均分”。
按此规定,该运动员得分是:
这个平均数是叫做截尾平均数。
去掉7.5和9.5,
例1:某班9位同学参加一分钟跳短绳测试项目,成绩分别为(个/每分钟)
98,91,100,93,103,167,105,91,115
(1)这组数据的平均数是一分钟多少个?
(2)这组数据的中位数是一分钟多少个?
(3)这组数据的众数是一分钟多少个?
(4)你认为应该使用上述哪一个量来表示班级跳绳的平均水平比较合适?
上海国际半程马拉松赛于4月22日在上海东方明珠塔下开跑。15000名跑者踏上充满活力与美丽的赛道,经南浦大桥、世博大道、前滩公园,奔向终点东方体育中心。
半程马拉松:二分之一马拉松,目前国际上从众增长最快的赛跑项目。路程长度是21.0975公里,或13.1英里。因为半程马拉松的程长很有挑战性,但对跑步者的要求又不像全程马拉松那么严苛。
马拉松:国际上非常普及的长跑比赛项目,全程距离26英里385码,折合为42.195公里。分全程马拉松、半程马拉松和四分马拉松三种。
半程马拉松的最好成绩:
男子:厄立特里亚选手Zersenay
Tadese于2010年3月21日在葡萄牙里斯本创造的58:23。
女子:肯尼亚选手乔塞琳·杰普科西盖于2017年4月1日在布拉格创造的1:04:52。
练习1:在半程马拉松比赛中,获得其中12名选手的成绩如下(单位:分)
85 90 79 130
74
104
95
96
108
126 115 98
(1)样本数据(12名选手的成绩)的平均数是多少?
(2)样本数据(12名选手的成绩)的中位数是多少?
(3)一名选手的成绩是92分,他的成绩如何?
由(1)中样本数据的结论可以估计,在这次马拉松比赛的总体成绩中,约有一半的选手的成绩慢于97分,约有一半的选手的成绩快于97分,故成绩为92分钟的选手比一半以上选手的成绩要好。
(1)平均数:100
(2)中位数:97
不同点:
计算平均数时,所有数据都参加运算,它能充分利用所有数据提供的信息,但容易受极端值的影响。它应用最为广泛。
中位数的优点是计算简单,不受极端值的影响,只与其在数据中的位置有关。但不能充分利用所有的数据信息。一组数据的中位数是唯一的。
众数不受极端值的影响,只与其在数据中重复的次数有关,而且往往不是唯一的。
但不能充分利用所有的数据信息,而且当各个数据的重复次数大致相等时,众数往往没有特别的意义。
平均数、中位数和众数有哪些共同点和不同点?
共同点:都反映一组数据的平均水平,它们是表示一组数据平均水平的量。
例2:
某中学对40名男同学所穿运动鞋的尺码进行调查,
调查结果如下表:
尺码
37
38
39
40
41
42
人数
2
8
8
19
2
1
学校商店进货时,应该考虑多进哪种尺码的男式运动鞋?这个号码是平均数、中位数、众数中的哪一个数?
练习2:某初级中学提倡篮球运动,将投篮命中率作为考查学生体育成绩的一个项目,为了制定切合本校学生实际合格的标准,从各年级随机抽取50名学生进行10次投篮命中次数的测验,结果如图所示:
次数
0
1
2
3
4
5
6
7
8
9
10
人数
1
8
10
7
6
6
5
4
1
2
0
(1)求测试数据的平均数、中位数和众数。
(2)你认为哪一个表示平均水平的量作为标准较为合适?试简要说明理由。
(1)平均数:3.74
中位数:3
众数:2
中位数:将n个数据按大小依次排列,当n为奇数时,居中的一个数据,称为这组数据的中位数;当n为偶数时,居中两个数据的平均数,称为这组数据的中位数。
众数:在一组数据中,出现次数最多的数据叫做这组数据的众数。
