27.1 圆的确定 课件(30张PPT)
文档属性
| 名称 | 27.1 圆的确定 课件(30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 839.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 11:24:12 | ||
图片预览








文档简介
(共30张PPT)
27.1
圆的确定
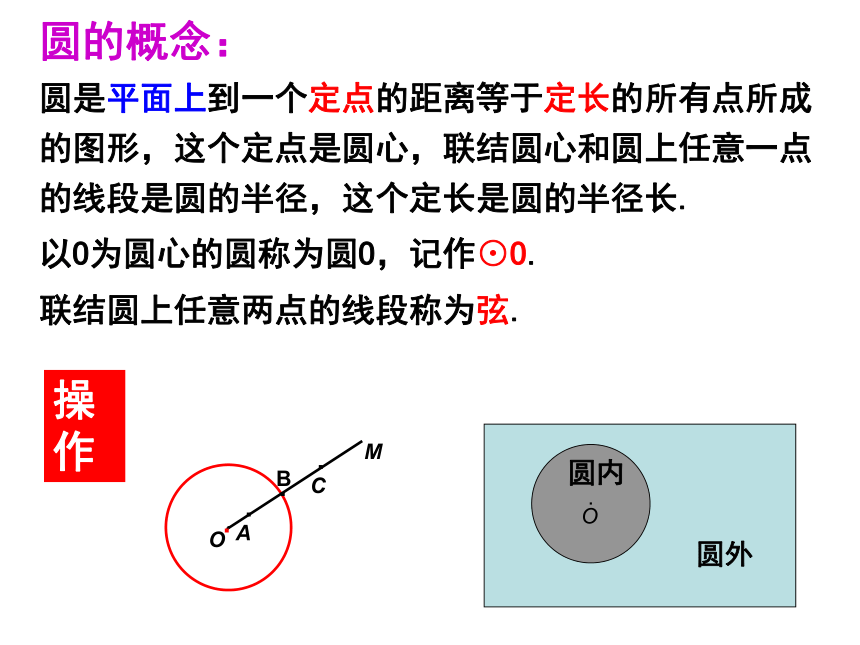
圆的概念:
圆是平面上到一个定点的距离等于定长的所有点所成的图形,这个定点是圆心,联结圆心和圆上任意一点的线段是圆的半径,这个定长是圆的半径长.
·
以O为圆心的圆称为圆O,记作⊙O.
操作
O
·
·
·
·
A
B
C
M
·
O
圆内
圆外
联结圆上任意两点的线段称为弦.
点和圆的位置关系:
对于给定的一个圆,平面上的点与这个圆的位置关系有三种:
点在圆内,点在圆上,点在圆外.
设圆的半径长为R,点P
到圆心的距离为d,则
点P
在圆外
d
>R;
点P
在圆上
d
=R;
点P
在圆内
d
例题1
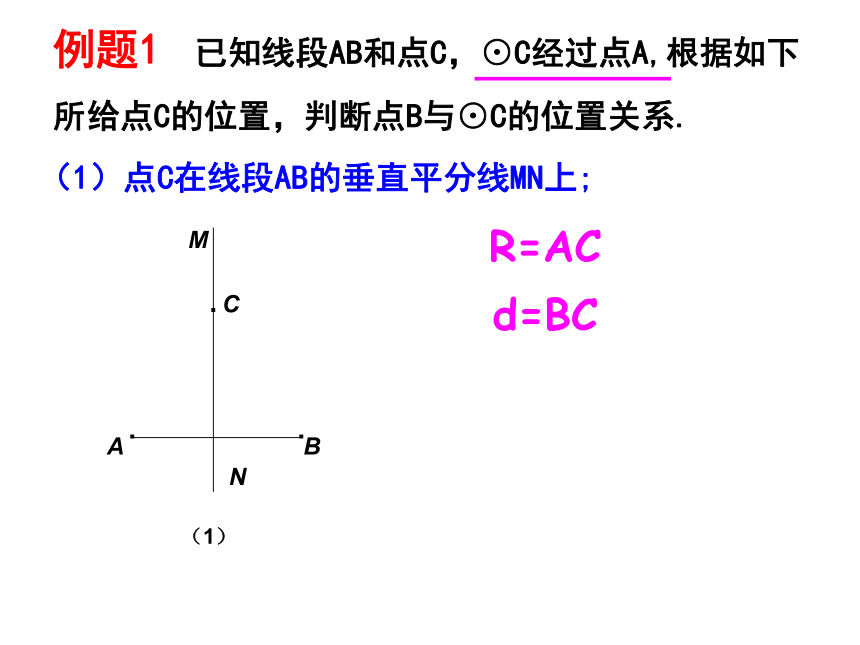
已知线段AB和点C,⊙C经过点A,根据如下所给点C的位置,判断点B与⊙C的位置关系.
(1)点C在线段AB的垂直平分线MN上;
M
N
·
·
·
(1)
A
B
C
R=AC
d=BC
(2)点C在线段AB上且0
<
AC
<
AB.
·
·
·
A
B
C
(2)
例题1
已知线段AB和点C,⊙C经过点A,根据如下所给点C的位置,判断点B与⊙C的位置关系.
一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
要确定一个圆
必须满足几个条件
1、过一点可以作几条直线?
2、过几点可确定一条直线?
过几点可以确定一个圆呢?
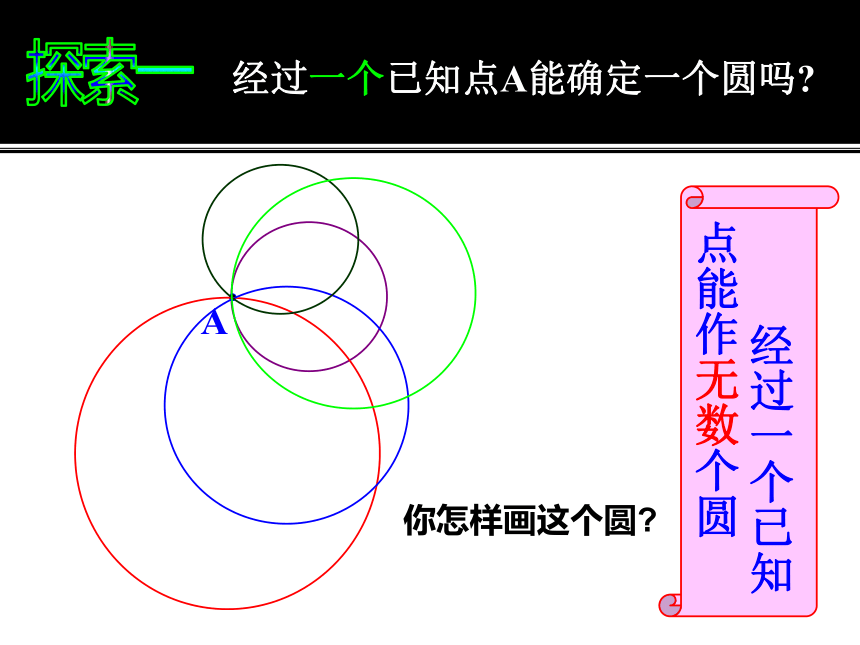
经过一个已知点A能确定一个圆吗
A
经过一个已知点能作无数个圆
你怎样画这个圆
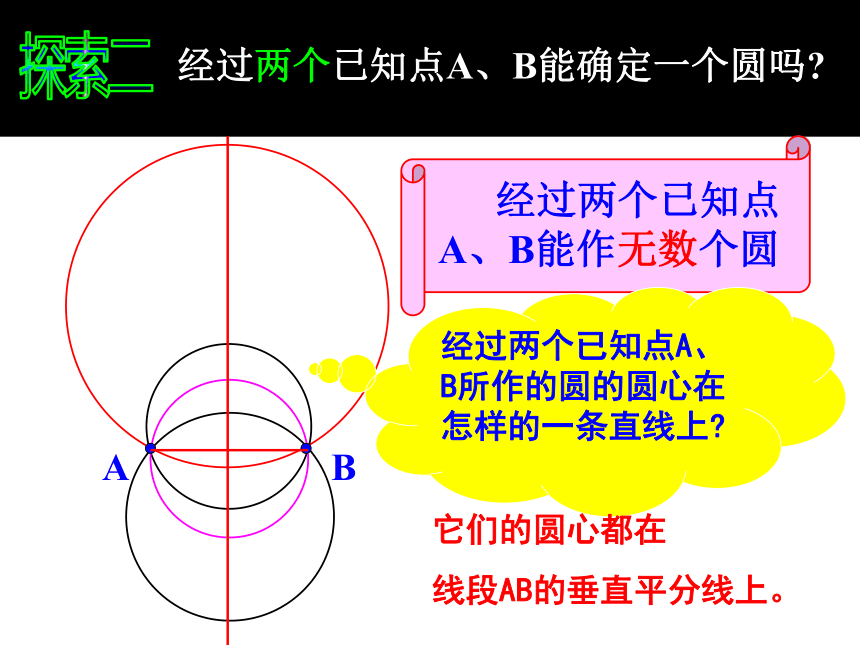
经过两个已知点A、B能确定一个圆吗
A
B
经过两个已知点A、B能作无数个圆
经过两个已知点A、B所作的圆的圆心在怎样的一条直线上
它们的圆心都在
线段AB的垂直平分线上。
A、B、C三点的⊙O有且只有一个。
(2)AB、AC的垂直平分线
MN、EF的交点为点O。
N
M
F
E
O
A
B
C
经过三个已知点A、B、C能确定一个圆吗?
所以,经过
(1)联结AB、AC,
作AB的垂直平分线MN,
作AC的垂直平分线EF,
不共线
定理
不在同一直线上的三个点确定一个圆.
A
B
C
过如下三点能不能做圆
为什么
N
M
F
E
三角形与圆的位置关系
三角形的三个顶点确定一个圆,经过三角形各顶点的圆叫做三角形的外接圆.外接圆的圆心叫做三角形的外心.
这个三角形叫做圆的内接三角形.
外接圆的圆心是
●O
A
B
C
如果一个圆经过一个多边形的各顶点,
那么这个圆叫做这个多边形的外接圆,
这个多边形叫做这个圆的内接多边形.
三角形三边垂直平分线的的交点.
例题2
已知钝角三角形ABC,
用直尺和圆规作出这个三角形的外接圆.
A
B
C
·
O
D
E
作法:
1.作线段AB的垂直平分线l1.
2.作线段AC的垂直平分线l2.
3.以点O为圆心,OA为半径作⊙O
⊙O
就是所求作的圆.
即求作过点A、B、C三点的圆.
现在你知道了怎样要将一个如图所示的破损的圆盘复原了吗?
方法:
1、在圆弧上任取三点A、B、C。
2、作线段AB、BC的垂直平分线,其交点O即为圆心。
3、以点O为圆心,OC长为半径作圆。
⊙O即为所求。
A
B
C
O
画出过以下三角形的顶点的圆
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
1、比较这三个三角形外心的位置,你有何发现?
(图一)
(图二)
(图三)
2、图二中,若AB=3,BC=4,则它的外接圆半径是多少?
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
延伸拓展:
经过不在同一直线上的四点
是否一定能作一个圆?
D
A
B
C
试一试
如图,在△ABC中,∠A为锐角,
BD⊥AC,CE⊥AB,D、E是垂足。
求证:B、C、D、E四个点在同一个圆上
∠A是钝角,
其他条件不变,
结论还成立吗?
A
B
C
E
D
O
A
B
C
D
E
某市要建一个圆形公园,要求公园刚好把动物园A,植物园B和人工湖C包括在内,又要使这个圆形的面积最小,请你给出这个公园的施工图。
(A、B、C不在同一直线上)
植物园
动物园
人工湖
练一练
1.下列命题不正确的是(
)
A.过一点有无数个圆.
B.过两点有无数个圆.
C.弦是圆的一部分.
D.过同一直线上三点不能画圆.
2.三角形的外心具有的性质是(
)
A.到三边的距离相等.
B.到三个顶点的距离相等.
C.外心在三角形的外.
D.外心在三角形内.
3.下列说法正确的是(
)
A.三点确定一个圆
B.三角形有且只有一个外接圆
C.四边形都有一个外接圆
D.圆有且只有一个内接三角形
4.下列命题中的假命题是(
)
A.三角形的外心到三角形各顶点的距离相等
B.三角形的外心到三角形三边的距离相等
C.三角形的外心一定在三角形一边的中垂线上
D.三角形任意两边的中垂线的交点,
是这个三角形的外心
练一练
4.下列图形一定有外接圆的是(
)
A.三角形
B.平行四边形
C.梯形
D.菱形
练一练
5.经过平面上一点可以画
个圆;经过平面上
两点A、B可以作
个圆,这些圆的圆心在
.
6.过平面上不在同一直线上的三点可以作
个圆.
7.锐角三角形的外心在
;
直角三角形的外心在
;
钝角三角形的外心在
.
8.等边三角形的外接圆的半径等于边长的
倍.
无数
无数
线段AB的中垂线上
一
三角形内
斜边中点
三角形外
9.判断题.
(1)经过三个点一定可以作圆.
(
)
(2)任意一个三角形一定有一个外接圆,
并且只有一个外接圆.
(
)
(3)任意一个圆一定有一个内接三角形,
并且只有一个内接三角形.
(
)
(4)三角形的外心到三角形各顶点的距离相等.(
)
练一练
(5)三角形的外心就是这个三角形两边垂直平分线
的交点.
(
)
(6)三角形的外心到三边的距离相等.
(
)
(7)等腰三角形的外心一定在这个三角形内.
(
)
×
√
×
√
√
×
×
10.
在△ABC中,BC=24cm,
外心O到BC的距离为6cm,
求△ABC的外接圆半径
练一练
12
6
11.
已知Rt△ABC的两直角边为a和b,
且a,b是方程x2-3x+1=0的两根,
求Rt△ABC的外接圆面积.
练一练
(1)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定。
(2)经过一个已知点能作无数个圆!
(3)经过两个已知点A、B能作无数个圆!这些圆的圆心在线段AB的垂直平分线上。
(4)不在同一直线上的三个点确定一个圆。
(5)外接圆,外心的概念。
开放性综合题
如图,在平面直角坐标系xOy中,有点A(4,0),
B(
,0),C(0,3),以C为圆心、5为半径作⊙C。
(1)分别判断点A、B和⊙C的位置关系;
(2)设P是x轴上的一个动点,
当点P的横坐标xP在什么范围内时,
点P一定在⊙C的内部?
27.1
圆的确定
圆的概念:
圆是平面上到一个定点的距离等于定长的所有点所成的图形,这个定点是圆心,联结圆心和圆上任意一点的线段是圆的半径,这个定长是圆的半径长.
·
以O为圆心的圆称为圆O,记作⊙O.
操作
O
·
·
·
·
A
B
C
M
·
O
圆内
圆外
联结圆上任意两点的线段称为弦.
点和圆的位置关系:
对于给定的一个圆,平面上的点与这个圆的位置关系有三种:
点在圆内,点在圆上,点在圆外.
设圆的半径长为R,点P
到圆心的距离为d,则
点P
在圆外
d
>R;
点P
在圆上
d
=R;
点P
在圆内
d
已知线段AB和点C,⊙C经过点A,根据如下所给点C的位置,判断点B与⊙C的位置关系.
(1)点C在线段AB的垂直平分线MN上;
M
N
·
·
·
(1)
A
B
C
R=AC
d=BC
(2)点C在线段AB上且0
<
AC
<
AB.
·
·
·
A
B
C
(2)
例题1
已知线段AB和点C,⊙C经过点A,根据如下所给点C的位置,判断点B与⊙C的位置关系.
一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
要确定一个圆
必须满足几个条件
1、过一点可以作几条直线?
2、过几点可确定一条直线?
过几点可以确定一个圆呢?
经过一个已知点A能确定一个圆吗
A
经过一个已知点能作无数个圆
你怎样画这个圆
经过两个已知点A、B能确定一个圆吗
A
B
经过两个已知点A、B能作无数个圆
经过两个已知点A、B所作的圆的圆心在怎样的一条直线上
它们的圆心都在
线段AB的垂直平分线上。
A、B、C三点的⊙O有且只有一个。
(2)AB、AC的垂直平分线
MN、EF的交点为点O。
N
M
F
E
O
A
B
C
经过三个已知点A、B、C能确定一个圆吗?
所以,经过
(1)联结AB、AC,
作AB的垂直平分线MN,
作AC的垂直平分线EF,
不共线
定理
不在同一直线上的三个点确定一个圆.
A
B
C
过如下三点能不能做圆
为什么
N
M
F
E
三角形与圆的位置关系
三角形的三个顶点确定一个圆,经过三角形各顶点的圆叫做三角形的外接圆.外接圆的圆心叫做三角形的外心.
这个三角形叫做圆的内接三角形.
外接圆的圆心是
●O
A
B
C
如果一个圆经过一个多边形的各顶点,
那么这个圆叫做这个多边形的外接圆,
这个多边形叫做这个圆的内接多边形.
三角形三边垂直平分线的的交点.
例题2
已知钝角三角形ABC,
用直尺和圆规作出这个三角形的外接圆.
A
B
C
·
O
D
E
作法:
1.作线段AB的垂直平分线l1.
2.作线段AC的垂直平分线l2.
3.以点O为圆心,OA为半径作⊙O
⊙O
就是所求作的圆.
即求作过点A、B、C三点的圆.
现在你知道了怎样要将一个如图所示的破损的圆盘复原了吗?
方法:
1、在圆弧上任取三点A、B、C。
2、作线段AB、BC的垂直平分线,其交点O即为圆心。
3、以点O为圆心,OC长为半径作圆。
⊙O即为所求。
A
B
C
O
画出过以下三角形的顶点的圆
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
1、比较这三个三角形外心的位置,你有何发现?
(图一)
(图二)
(图三)
2、图二中,若AB=3,BC=4,则它的外接圆半径是多少?
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
延伸拓展:
经过不在同一直线上的四点
是否一定能作一个圆?
D
A
B
C
试一试
如图,在△ABC中,∠A为锐角,
BD⊥AC,CE⊥AB,D、E是垂足。
求证:B、C、D、E四个点在同一个圆上
∠A是钝角,
其他条件不变,
结论还成立吗?
A
B
C
E
D
O
A
B
C
D
E
某市要建一个圆形公园,要求公园刚好把动物园A,植物园B和人工湖C包括在内,又要使这个圆形的面积最小,请你给出这个公园的施工图。
(A、B、C不在同一直线上)
植物园
动物园
人工湖
练一练
1.下列命题不正确的是(
)
A.过一点有无数个圆.
B.过两点有无数个圆.
C.弦是圆的一部分.
D.过同一直线上三点不能画圆.
2.三角形的外心具有的性质是(
)
A.到三边的距离相等.
B.到三个顶点的距离相等.
C.外心在三角形的外.
D.外心在三角形内.
3.下列说法正确的是(
)
A.三点确定一个圆
B.三角形有且只有一个外接圆
C.四边形都有一个外接圆
D.圆有且只有一个内接三角形
4.下列命题中的假命题是(
)
A.三角形的外心到三角形各顶点的距离相等
B.三角形的外心到三角形三边的距离相等
C.三角形的外心一定在三角形一边的中垂线上
D.三角形任意两边的中垂线的交点,
是这个三角形的外心
练一练
4.下列图形一定有外接圆的是(
)
A.三角形
B.平行四边形
C.梯形
D.菱形
练一练
5.经过平面上一点可以画
个圆;经过平面上
两点A、B可以作
个圆,这些圆的圆心在
.
6.过平面上不在同一直线上的三点可以作
个圆.
7.锐角三角形的外心在
;
直角三角形的外心在
;
钝角三角形的外心在
.
8.等边三角形的外接圆的半径等于边长的
倍.
无数
无数
线段AB的中垂线上
一
三角形内
斜边中点
三角形外
9.判断题.
(1)经过三个点一定可以作圆.
(
)
(2)任意一个三角形一定有一个外接圆,
并且只有一个外接圆.
(
)
(3)任意一个圆一定有一个内接三角形,
并且只有一个内接三角形.
(
)
(4)三角形的外心到三角形各顶点的距离相等.(
)
练一练
(5)三角形的外心就是这个三角形两边垂直平分线
的交点.
(
)
(6)三角形的外心到三边的距离相等.
(
)
(7)等腰三角形的外心一定在这个三角形内.
(
)
×
√
×
√
√
×
×
10.
在△ABC中,BC=24cm,
外心O到BC的距离为6cm,
求△ABC的外接圆半径
练一练
12
6
11.
已知Rt△ABC的两直角边为a和b,
且a,b是方程x2-3x+1=0的两根,
求Rt△ABC的外接圆面积.
练一练
(1)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定。
(2)经过一个已知点能作无数个圆!
(3)经过两个已知点A、B能作无数个圆!这些圆的圆心在线段AB的垂直平分线上。
(4)不在同一直线上的三个点确定一个圆。
(5)外接圆,外心的概念。
开放性综合题
如图,在平面直角坐标系xOy中,有点A(4,0),
B(
,0),C(0,3),以C为圆心、5为半径作⊙C。
(1)分别判断点A、B和⊙C的位置关系;
(2)设P是x轴上的一个动点,
当点P的横坐标xP在什么范围内时,
点P一定在⊙C的内部?
