27.5 圆与圆的位置关系(1) 课件(29张PPT)
文档属性
| 名称 | 27.5 圆与圆的位置关系(1) 课件(29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 319.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
27.5(1)圆与圆的位置关系
一、复习引入
问:直线与圆有几种位置关系 各是怎样定义的
直线与圆没有公共点叫做直线与圆相离.
直线与圆有唯一公共点时,叫做直线与圆相切.
直线与圆有两个公共点时,叫做直线与圆相交.
答:直线与圆有三种位置关系:
相离、相切、相交.
各种位置关系是通过直线与圆的公共点的个数来定义的.
问:直线与圆的位置关系中,可以用怎样的数量关系来描述
答:若r表示圆的半径,d表示圆心到直线的距离.
则
直线与圆相交
0≤d
<r
直线与圆相切
d=r
直线与圆相离
d>r
一、复习引入
二、小组合作探究
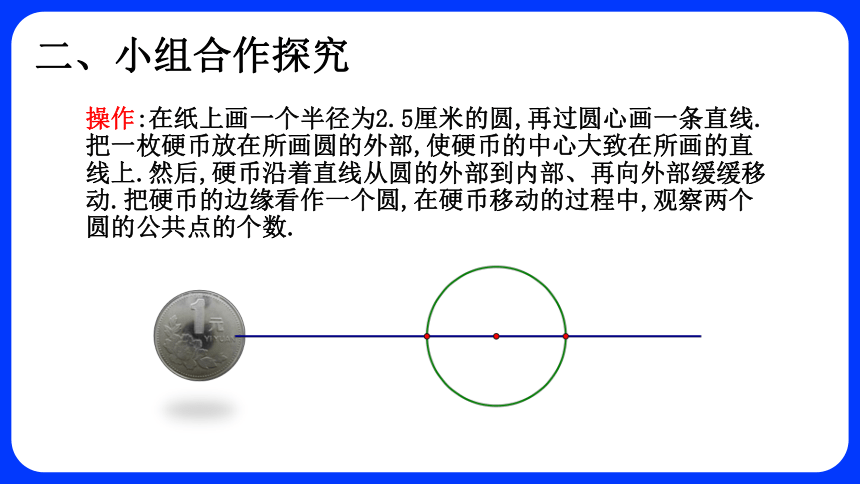
操作:在纸上画一个半径为2.5厘米的圆,再过圆心画一条直线.把一枚硬币放在所画圆的外部,使硬币的中心大致在所画的直线上.然后,硬币沿着直线从圆的外部到内部、再向外部缓缓移动.把硬币的边缘看作一个圆,在硬币移动的过程中,观察两个圆的公共点的个数.
二.新知探究
问1:通过操作可以看到,两个圆的公共点的个数有几种情况
答:三种.
问2:有哪三种
没有公共点.
有唯一公共点
有两个公共点
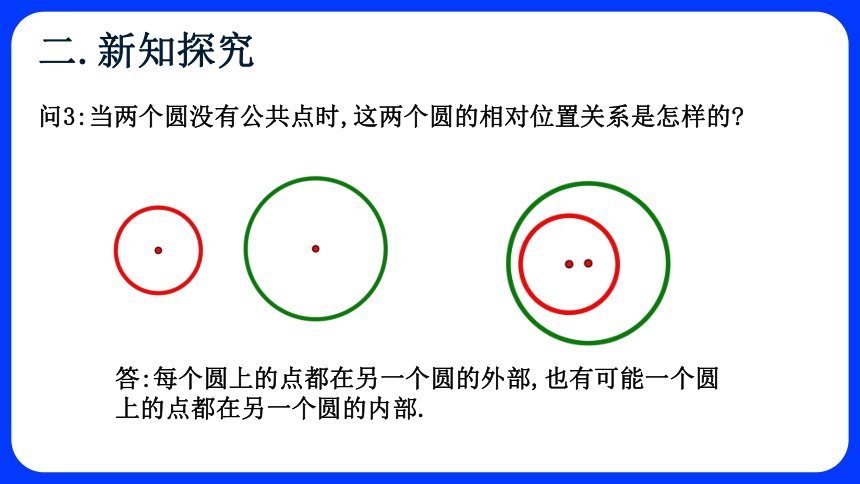
问3:当两个圆没有公共点时,这两个圆的相对位置关系是怎样的
答:每个圆上的点都在另一个圆的外部,也有可能一个圆上的点都在另一个圆的内部.
二.新知探究
问4:当两个圆有唯一公共点时,这两个圆的相对位置关系又是怎样的
答:除公共点以外,每个圆上的点都在另一个圆的外部,也有可能一个圆上的点都在另一个圆的内部.
二.新知探究
1、归纳两圆位置关系:
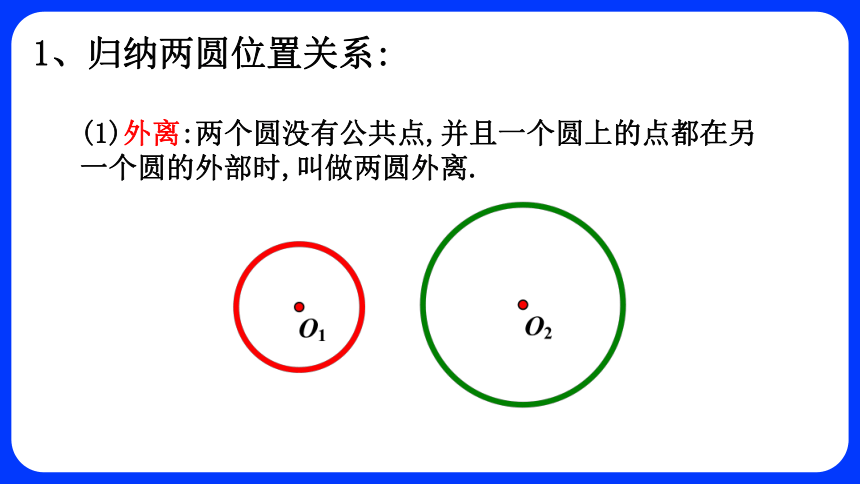
(1)外离:两个圆没有公共点,并且一个圆上的点都在另一个圆的外部时,叫做两圆外离.
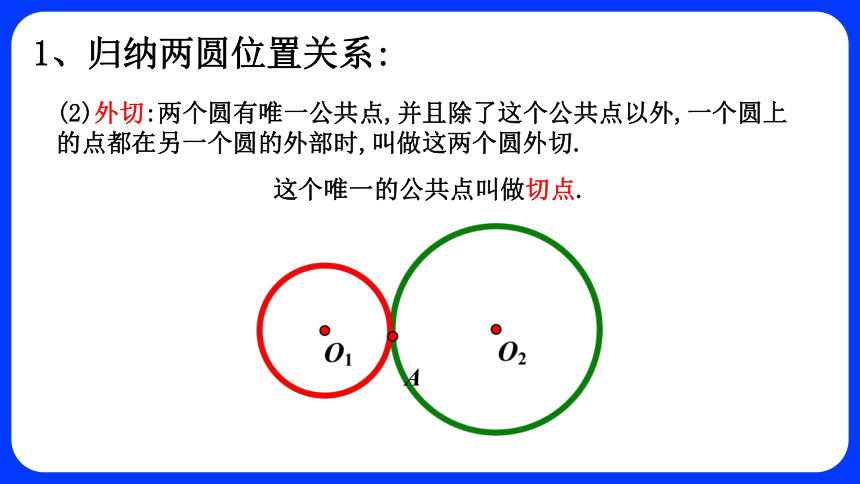
(2)外切:两个圆有唯一公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的外部时,叫做这两个圆外切.
A
这个唯一的公共点叫做切点.
1、归纳两圆位置关系:
(3)相交:两个圆有两个公共点,此时叫做两圆相交.
A
B
1、归纳两圆位置关系:
(4)内切:两个圆有唯一公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切.
这个唯一的公共点叫做切点.
A
半径相等的两个圆会内切吗?
1、归纳两圆位置关系:
(5)内含:两个圆没有公共点,并且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含.
两圆同心是两圆内含的一个特例.
半径相等的两个圆会内含吗?
1、归纳两圆位置关系:
问5:能否从两圆公共点的个数来归纳两圆的位置关系?
答:无交点:
相离
外离
内含
有一个交点:
相切
外切
内切
有两个交点:
相交
结论:在同一平面内任意两圆只存在以上三类五种位置关系.
2.两圆位置关系的数量特征
概念:
(1)两个圆的圆心之间的距离叫做圆心距.
(2)经过两个圆的圆心的直线叫做连心线.
设两圆的半径分别为R1和R2,圆心距为d
.
问:类比直线与圆的位置关系,你能用数量关系来描述圆与圆之间的位置关系吗
这些数量关系可以借助于图形的直观性来推导.
2.两圆位置关系的数量特征
三.例题讲解
例1
已知⊙O1和⊙O2的半径长分别为3和4,根据下列条件判断⊙O1和⊙O2的位置关系:
(1)
O1
O2=7;(2)
O1
O2=4;
(3)
O1
O2=0.5;
解:分别用R1、R2、d
表示⊙O1和⊙O2的半径和圆心距
.
由R1=3和R2=4得
R1+R2=7,∣R1-R2∣=1
(1)∵d=7
∴d=R1+R2
所以⊙O1和⊙O2的位置关系是外切.
解:分别用R1、R2、d
表示⊙O1和⊙O2的半径和圆心距
.
由R1=3和R2=4得
R1+R2=7,∣R1-R2∣=1
(2)∵d=4
∴
∣R1-R2∣<
d
<R1+R2
所以⊙O1和⊙O2的位置关系是相交.
三.例题讲解
例1
已知⊙O1和⊙O2的半径长分别为3和4,根据下列条件判断⊙O1和⊙O2的位置关系:
(1)
O1
O2=7;(2)
O1
O2=4;
(3)
O1
O2=0.5;
解:分别用R1、R2、d
表示⊙O1和⊙O2的半径和圆心距
.
由R1=3和R2=4得
R1+R2=7,∣R1-R2∣=1
(3)∵d=0.5
∴0≤d
<∣R1-R2∣
所以⊙O1和⊙O2的位置关系是内含.
三.例题讲解
例1
已知⊙O1和⊙O2的半径长分别为3和4,根据下列条件判断⊙O1和⊙O2的位置关系:
(1)
O1
O2=7;(2)
O1
O2=4;
(3)
O1
O2=0.5;
适时小结
例1
已知⊙O1和⊙O2的半径长分别为3和4,根据下列条件
判断⊙O1和⊙O2的位置关系:
(1)
O1
O2=7;(2)
O1
O2=4;
(3)
O1
O2=0.5;
解:分别用R1、R2、d
表示⊙O1和⊙O2的半径和圆心距
.
由R1=3和R2=4得
R1+R2=7,∣R1-R2∣=1
(1)∵d=7
∴d=R1+R2
所以⊙O1和⊙O2的位置关系是外切.
(2)∵d=4
∴
∣R1-R2∣<
d
<R1+R2
所以⊙O1和⊙O2的位置关系是相交.
(3)∵d=0.5
∴0≤d
<∣R1-R2∣
所以⊙O1和⊙O2的位置关系是内含.
如何判断两圆的位置关系?
先求出R1+R2和∣R1-R2∣的值
然后比较得出圆心距满足的关系式
最后得出两圆的位置关系
四、巩固练习
1.判断题
(1)⊙O1和⊙O2的半径长为R1、R2,圆心距为d,如果R1=1,R2=2,
d=0.5,那么⊙O1和⊙O2相交.
(
)
(2)
⊙O1和⊙O2的半径长为R1、R2,如果R1=5,R2=3,
且⊙O1和⊙O2相切,圆心距d=8.
(
)
(3)如果两圆相离,那么圆心距一定大于0.
(
)
0≤d<∣R1-R2∣
两圆内含
错
圆与圆相切包括外切和内切两种
d=8或2
错
两圆相离包括外离和内含两种
d>3或0≤d<1
错
2.
已知⊙O1和⊙O2的半径长分别为1和3,根据下列条件判断⊙O1和⊙O2的位置关系
(1)O1
O2=5;
(2)O1
O2=4;
(3)
O1
O2=3;
(4)O1
O2=2;
(5)O1
O2=1;
∵O1O2>R1+R2,∴两圆外离
∵O1O2=
R1+R2,∴两圆外切
∵∣R1-R2∣<O1O2<R1+R2,
∴两圆相交
∵O1O2=
∣R1-R2∣,∴两圆内切
∵0≤O1O2=
∣R1-R2∣,∴两圆内含
R1+R2=4,
∣R1-R2∣=2
四、巩固练习
三、例题讲解
例2
如图,已知⊙A、
⊙B、
⊙C两两外切,且AB=3厘米,BC=5厘米,AC=6厘米,
求:这三个圆的半径长.
问1:
⊙A、
⊙B、
⊙C两两外切
表示什么意思
RA+RB=AB,
RA+RC=AC,
RB+RC=BC
问2:用怎样的方法求这三个圆的半径?
设元,列出三元一次方程组.
解:
设⊙A、
⊙B、
⊙C的半径长分
别为x厘米、y厘米、z厘米
∴AB=x+y,
BC=y+z,
AC=z+x,
∵
⊙A、
⊙B、
⊙C两两外切
根据题意得关于x、y、z的方程组
∴⊙A、
⊙B、
⊙C的半径长分别为2厘米、1厘米、4厘米.
x+y=3
y+z=5
z+x=6
x=2
解得
y=1
z=4
三、例题讲解
例2
如图,已知⊙A、
⊙B、
⊙C两两外切,且AB=3厘米,BC=5厘米,AC=6厘米,
求:这三个圆的半径长.
五、独立完成后测单
3.已知两圆的直径长分别为6厘米和8厘米,圆心距为14厘米,试说明这两个圆的位置关系.
解:∵两圆的直径长分别为6厘米和8厘米
∴R1=3厘米,R2=4厘米
∵d=14厘米
∴
R1+R2=7厘米,
∣R1-R2∣=1厘米
∴d>R1+R2
∴两圆外离
4.
已知两圆内切,圆心距为2厘米,其中一个圆的半径长为3厘米,求另一个圆的半径长.
解:设另一个圆的半径长为R.
根据题意,得∣R-3∣=2,
R-3=±2,
∴R1=5厘米,R2=1厘米.
答:另一个圆的半径为5厘米或1厘米.
五、独立完成后测单
已知两圆的半径长R、r和它们的圆心距d满足关系式
,判定两个圆的位置关系.
六、拓展应用
解:
因此两圆位置关系为相切.
七、课堂小结
两圆的三类五种位置关系下圆心距和两圆半径的数量关系:
两圆外离
d>R1+R2
两圆外切
d=
R1+R2
两圆相交
∣R1-R2∣<d<R1+R2
两圆内切
0<d=
∣R1-R2∣
两圆内含
0≤d<∣R1-R2∣
无交点:
两圆相离
有一个交点:
两圆相切
有两个交点:
两圆相交
八、作业布置
练习册
习题27.5(1)
Thank
you
27.5(1)圆与圆的位置关系
一、复习引入
问:直线与圆有几种位置关系 各是怎样定义的
直线与圆没有公共点叫做直线与圆相离.
直线与圆有唯一公共点时,叫做直线与圆相切.
直线与圆有两个公共点时,叫做直线与圆相交.
答:直线与圆有三种位置关系:
相离、相切、相交.
各种位置关系是通过直线与圆的公共点的个数来定义的.
问:直线与圆的位置关系中,可以用怎样的数量关系来描述
答:若r表示圆的半径,d表示圆心到直线的距离.
则
直线与圆相交
0≤d
<r
直线与圆相切
d=r
直线与圆相离
d>r
一、复习引入
二、小组合作探究
操作:在纸上画一个半径为2.5厘米的圆,再过圆心画一条直线.把一枚硬币放在所画圆的外部,使硬币的中心大致在所画的直线上.然后,硬币沿着直线从圆的外部到内部、再向外部缓缓移动.把硬币的边缘看作一个圆,在硬币移动的过程中,观察两个圆的公共点的个数.
二.新知探究
问1:通过操作可以看到,两个圆的公共点的个数有几种情况
答:三种.
问2:有哪三种
没有公共点.
有唯一公共点
有两个公共点
问3:当两个圆没有公共点时,这两个圆的相对位置关系是怎样的
答:每个圆上的点都在另一个圆的外部,也有可能一个圆上的点都在另一个圆的内部.
二.新知探究
问4:当两个圆有唯一公共点时,这两个圆的相对位置关系又是怎样的
答:除公共点以外,每个圆上的点都在另一个圆的外部,也有可能一个圆上的点都在另一个圆的内部.
二.新知探究
1、归纳两圆位置关系:
(1)外离:两个圆没有公共点,并且一个圆上的点都在另一个圆的外部时,叫做两圆外离.
(2)外切:两个圆有唯一公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的外部时,叫做这两个圆外切.
A
这个唯一的公共点叫做切点.
1、归纳两圆位置关系:
(3)相交:两个圆有两个公共点,此时叫做两圆相交.
A
B
1、归纳两圆位置关系:
(4)内切:两个圆有唯一公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切.
这个唯一的公共点叫做切点.
A
半径相等的两个圆会内切吗?
1、归纳两圆位置关系:
(5)内含:两个圆没有公共点,并且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含.
两圆同心是两圆内含的一个特例.
半径相等的两个圆会内含吗?
1、归纳两圆位置关系:
问5:能否从两圆公共点的个数来归纳两圆的位置关系?
答:无交点:
相离
外离
内含
有一个交点:
相切
外切
内切
有两个交点:
相交
结论:在同一平面内任意两圆只存在以上三类五种位置关系.
2.两圆位置关系的数量特征
概念:
(1)两个圆的圆心之间的距离叫做圆心距.
(2)经过两个圆的圆心的直线叫做连心线.
设两圆的半径分别为R1和R2,圆心距为d
.
问:类比直线与圆的位置关系,你能用数量关系来描述圆与圆之间的位置关系吗
这些数量关系可以借助于图形的直观性来推导.
2.两圆位置关系的数量特征
三.例题讲解
例1
已知⊙O1和⊙O2的半径长分别为3和4,根据下列条件判断⊙O1和⊙O2的位置关系:
(1)
O1
O2=7;(2)
O1
O2=4;
(3)
O1
O2=0.5;
解:分别用R1、R2、d
表示⊙O1和⊙O2的半径和圆心距
.
由R1=3和R2=4得
R1+R2=7,∣R1-R2∣=1
(1)∵d=7
∴d=R1+R2
所以⊙O1和⊙O2的位置关系是外切.
解:分别用R1、R2、d
表示⊙O1和⊙O2的半径和圆心距
.
由R1=3和R2=4得
R1+R2=7,∣R1-R2∣=1
(2)∵d=4
∴
∣R1-R2∣<
d
<R1+R2
所以⊙O1和⊙O2的位置关系是相交.
三.例题讲解
例1
已知⊙O1和⊙O2的半径长分别为3和4,根据下列条件判断⊙O1和⊙O2的位置关系:
(1)
O1
O2=7;(2)
O1
O2=4;
(3)
O1
O2=0.5;
解:分别用R1、R2、d
表示⊙O1和⊙O2的半径和圆心距
.
由R1=3和R2=4得
R1+R2=7,∣R1-R2∣=1
(3)∵d=0.5
∴0≤d
<∣R1-R2∣
所以⊙O1和⊙O2的位置关系是内含.
三.例题讲解
例1
已知⊙O1和⊙O2的半径长分别为3和4,根据下列条件判断⊙O1和⊙O2的位置关系:
(1)
O1
O2=7;(2)
O1
O2=4;
(3)
O1
O2=0.5;
适时小结
例1
已知⊙O1和⊙O2的半径长分别为3和4,根据下列条件
判断⊙O1和⊙O2的位置关系:
(1)
O1
O2=7;(2)
O1
O2=4;
(3)
O1
O2=0.5;
解:分别用R1、R2、d
表示⊙O1和⊙O2的半径和圆心距
.
由R1=3和R2=4得
R1+R2=7,∣R1-R2∣=1
(1)∵d=7
∴d=R1+R2
所以⊙O1和⊙O2的位置关系是外切.
(2)∵d=4
∴
∣R1-R2∣<
d
<R1+R2
所以⊙O1和⊙O2的位置关系是相交.
(3)∵d=0.5
∴0≤d
<∣R1-R2∣
所以⊙O1和⊙O2的位置关系是内含.
如何判断两圆的位置关系?
先求出R1+R2和∣R1-R2∣的值
然后比较得出圆心距满足的关系式
最后得出两圆的位置关系
四、巩固练习
1.判断题
(1)⊙O1和⊙O2的半径长为R1、R2,圆心距为d,如果R1=1,R2=2,
d=0.5,那么⊙O1和⊙O2相交.
(
)
(2)
⊙O1和⊙O2的半径长为R1、R2,如果R1=5,R2=3,
且⊙O1和⊙O2相切,圆心距d=8.
(
)
(3)如果两圆相离,那么圆心距一定大于0.
(
)
0≤d<∣R1-R2∣
两圆内含
错
圆与圆相切包括外切和内切两种
d=8或2
错
两圆相离包括外离和内含两种
d>3或0≤d<1
错
2.
已知⊙O1和⊙O2的半径长分别为1和3,根据下列条件判断⊙O1和⊙O2的位置关系
(1)O1
O2=5;
(2)O1
O2=4;
(3)
O1
O2=3;
(4)O1
O2=2;
(5)O1
O2=1;
∵O1O2>R1+R2,∴两圆外离
∵O1O2=
R1+R2,∴两圆外切
∵∣R1-R2∣<O1O2<R1+R2,
∴两圆相交
∵O1O2=
∣R1-R2∣,∴两圆内切
∵0≤O1O2=
∣R1-R2∣,∴两圆内含
R1+R2=4,
∣R1-R2∣=2
四、巩固练习
三、例题讲解
例2
如图,已知⊙A、
⊙B、
⊙C两两外切,且AB=3厘米,BC=5厘米,AC=6厘米,
求:这三个圆的半径长.
问1:
⊙A、
⊙B、
⊙C两两外切
表示什么意思
RA+RB=AB,
RA+RC=AC,
RB+RC=BC
问2:用怎样的方法求这三个圆的半径?
设元,列出三元一次方程组.
解:
设⊙A、
⊙B、
⊙C的半径长分
别为x厘米、y厘米、z厘米
∴AB=x+y,
BC=y+z,
AC=z+x,
∵
⊙A、
⊙B、
⊙C两两外切
根据题意得关于x、y、z的方程组
∴⊙A、
⊙B、
⊙C的半径长分别为2厘米、1厘米、4厘米.
x+y=3
y+z=5
z+x=6
x=2
解得
y=1
z=4
三、例题讲解
例2
如图,已知⊙A、
⊙B、
⊙C两两外切,且AB=3厘米,BC=5厘米,AC=6厘米,
求:这三个圆的半径长.
五、独立完成后测单
3.已知两圆的直径长分别为6厘米和8厘米,圆心距为14厘米,试说明这两个圆的位置关系.
解:∵两圆的直径长分别为6厘米和8厘米
∴R1=3厘米,R2=4厘米
∵d=14厘米
∴
R1+R2=7厘米,
∣R1-R2∣=1厘米
∴d>R1+R2
∴两圆外离
4.
已知两圆内切,圆心距为2厘米,其中一个圆的半径长为3厘米,求另一个圆的半径长.
解:设另一个圆的半径长为R.
根据题意,得∣R-3∣=2,
R-3=±2,
∴R1=5厘米,R2=1厘米.
答:另一个圆的半径为5厘米或1厘米.
五、独立完成后测单
已知两圆的半径长R、r和它们的圆心距d满足关系式
,判定两个圆的位置关系.
六、拓展应用
解:
因此两圆位置关系为相切.
七、课堂小结
两圆的三类五种位置关系下圆心距和两圆半径的数量关系:
两圆外离
d>R1+R2
两圆外切
d=
R1+R2
两圆相交
∣R1-R2∣<d<R1+R2
两圆内切
0<d=
∣R1-R2∣
两圆内含
0≤d<∣R1-R2∣
无交点:
两圆相离
有一个交点:
两圆相切
有两个交点:
两圆相交
八、作业布置
练习册
习题27.5(1)
Thank
you
