江西省南昌市第八中学、第二十三中学、第十三中学2018-2019学年第一学期高二期末联考理科数学(解析版)
文档属性
| 名称 | 江西省南昌市第八中学、第二十三中学、第十三中学2018-2019学年第一学期高二期末联考理科数学(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 269.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 13:25:57 | ||
图片预览




文档简介
2018-2019学年高二(上)期末数学试卷(理科)
一、选择题(共12小题)
1.设z=+i,则|z|=( )
A. B. C. D.2
2.用反证法证明命题“若自然数a,b,c的和为偶数,则a,b,c中至少有一个偶数”时,对结论正确的反设为( )
A.a,b,c中至多有一个偶数
B.a,b,c中一个偶数都没有
C.a,b,c至多有一个奇数
D.a,b,c都是偶数
3.设,是向量,则“||=||”是“|+|=|﹣|”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
4.命题p:?x>0,x2﹣2x+1>0;命题q:?x0>0,﹣2x0+1≤0,下列选项真命题的是( )
A.¬p∧q B.p∧q C.p∨¬q D.¬p∧¬q
5.设函数y=f(x)可导,则等于( )
A.f'(1) B.3f'(1) C. D.以上都不对
6.椭圆中,以点M(1,2)为中点的弦所在直线斜率为( )
A. B. C. D.
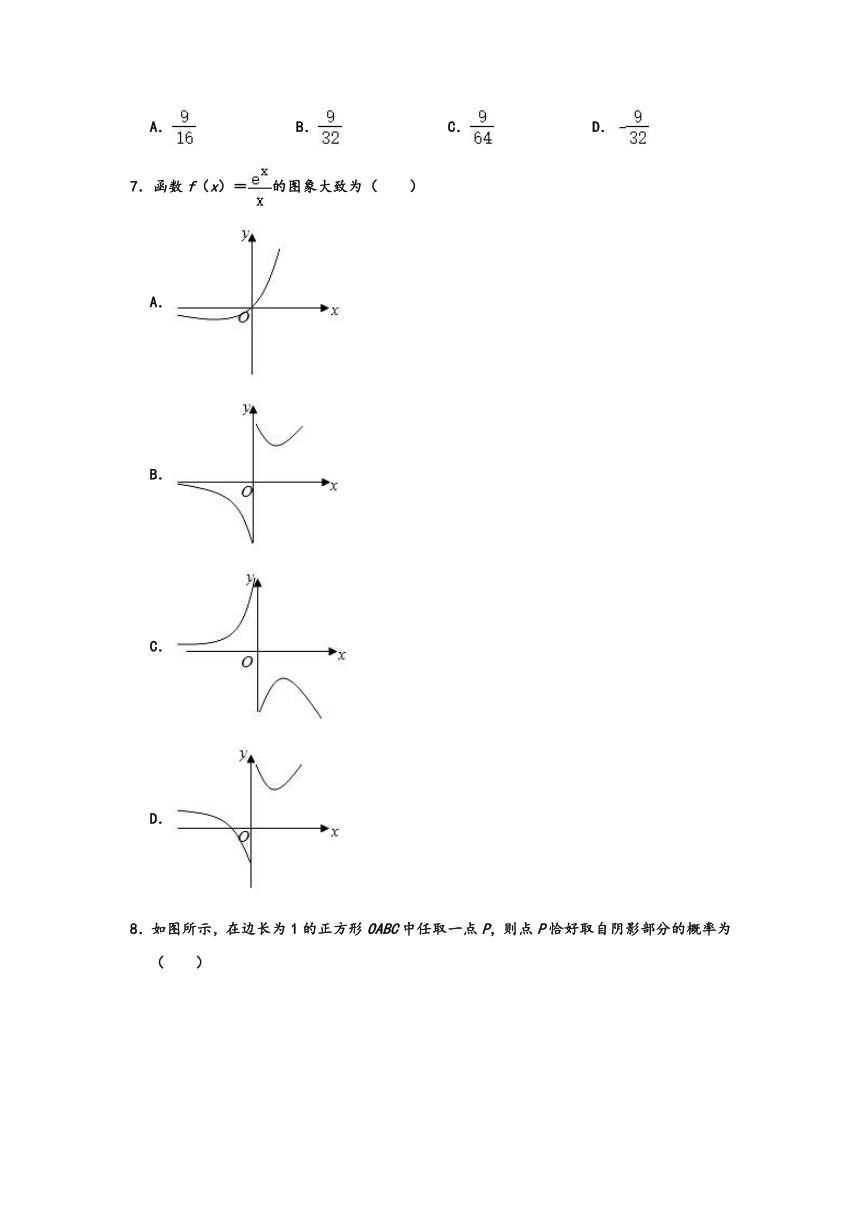
7.函数f(x)=的图象大致为( )
A.
B.
C.
D.
8.如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
A. B. C. D.
9.函数,则( )
A.x=e为函数f(x)的极大值点
B.x=e为函数f(x)的极小值点
C.为函数f(x)的极大值点
D.为函数f(x)的极小值点
10.已知f(x)=x2+2xf'(2016)﹣2016lnx,则f′(2016)=( )
A.2015 B.﹣2015 C.2016 D.﹣2016
11.已知点P在抛物线x2=4y上,则当点P到点Q(1,2)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
A.(2,1) B.(﹣2,1) C. D.
12.定义在R上的函数f(x)满足:f(x)+f′(x)>1,f(0)=4,则不等式exf(x)>ex+3(其中e为自然对数的底数)的解集为( )
A.(0,+∞) B.(﹣∞,0)∪(3,+∞)
C.(﹣∞,0)∪(0,+∞) D.(3,+∞)
二、填空题(共4小题)
13.定积分(x+ex)dx= .
14.已知复数z=m2(1+i)﹣m(3+6i)为纯虚数,则实数m= .
15.已知直线y=x﹣1与椭圆交于A、B两点,则线段AB的长为 .
16.给出下列命题:
①?x∈R,x3>x2;
②?x0∈R,使sin3x0=3sinx0;
③若a<b,则;
④设等差数列{an}前n项和为Sn,若S2016﹣S1=1,则S2017>1.
其中正确命题的序号是 .
三、解答題(本大题共6小题,共70分)
17.求出下列函数的导数.
(1)y=extanx
(2)y=ln(4x+5)3
(3)y=x
(4)y=
(5)y=e﹣x+2(2x+1)5
18.已知命题p:?x∈R,x2+1≥m;命题q:方程表示双曲线.
(1)若命题p为真命题,求实数m的取值范围;
(2)若命题“p∨q”为真命题,“p∧q”为假命题,求实数m的取值范围.
19.已知函数f(x)=x3﹣3x.
(Ⅰ)求函数f(x)在[﹣2,1]上的最大值和最小值.
(Ⅱ)过点P(2,﹣6)作曲线y=f(x)的切线,求此切线的方程.
20.已知函数f(x)=ex﹣x﹣1(e是自然对数的底数).
(1)求证:ex≥x+1;
(2)若不等式f(x)>ax﹣1在x∈[,2]上恒成立,求正数a的取值范围.
21.点是抛物上三点,其中0<a<2,并且A、B、C三点到焦点的距离成等差数列.
(Ⅰ)求抛物线方程;
(Ⅱ)证明:.
22.已知函数f(x)=ln﹣ax2+x,
(1)讨论函数f(x)的极值点的个数;
(2)若f(x)有两个极值点x1,x2,证明:f(x1)+f(x2)>3﹣4ln2.
参考答案
一、选择题(本大题共12小题,共60.0分)
1.设z=+i,则|z|=( )
A. B. C. D.2
解:z=+i=+i=.
故|z|==.
故选:B.
2.用反证法证明命题“若自然数a,b,c的和为偶数,则a,b,c中至少有一个偶数”时,对结论正确的反设为( )
A.a,b,c中至多有一个偶数
B.a,b,c中一个偶数都没有
C.a,b,c至多有一个奇数
D.a,b,c都是偶数
解:用反证法法证明数学命题时,应先假设要证的命题的反面成立,即要证的命题的否定成立,
而命题:“自然数a,b,c中至少有一个是偶数”的否定为:“a,b,c中一个偶数都没有”,
故选:B.
3.设,是向量,则“||=||”是“|+|=|﹣|”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
解:若“||=||”,则以,为邻边的平行四边形是菱形;
若“|+|=|﹣|”,则以,为邻边的平行四边形是矩形;
故“||=||”是“|+|=|﹣|”的既不充分也不必要条件;
故选:D.
4.命题p:?x>0,x2﹣2x+1>0;命题q:?x0>0,﹣2x0+1≤0,下列选项真命题的是( )
A.¬p∧q B.p∧q C.p∨¬q D.¬p∧¬q
解:命题p:?x>0,x2﹣2x+1>0;是假命题,因为x=1时不成立;
命题q:?x0>0,﹣2x0+1≤0,当x0=1时,命题成立,所以是真命题.
¬p∧q,是真命题;
p∧q是假命题;
p∨¬q是假命题;
¬p∧¬q是假命题;
故选:A.
5.设函数y=f(x)可导,则等于( )
A.f'(1) B.3f'(1) C. D.以上都不对
解:∵函数y=f(x)可导,
根据导数的定义式f′(x)=可得
∴=f'(1),
故选:A.
6.椭圆中,以点M(1,2)为中点的弦所在直线斜率为( )
A. B. C. D.
解:设弦的两端点为A(x1,y1),B(x2,y2),
代入椭圆得,
两式相减得+=0,
即=﹣,
即﹣=,
即﹣=,
即=,
∴弦所在的直线的斜率为,
故选:D.
7.函数f(x)=的图象大致为( )
A.
B.
C.
D.
解:函数f(x)=的定义域为:x≠0,x∈R,当x>0时,函数f′(x)=,可得函数的极值点为:x=1,当x∈(0,1)时,函数是减函数,x>1时,函数是增函数,并且f(x)>0,选项B、D满足题意.
当x<0时,函数f(x)=<0,选项D不正确,选项B正确.
故选:B.
8.如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
A. B. C. D.
解:根据题意,正方形OABC的面积为1×1=1,
而阴影部分由函数y=x与y=围成,其面积为∫01(﹣x)dx=(﹣)|01=,
则正方形OABC中任取一点P,点P取自阴影部分的概率为=;
故选:C.
9.函数,则( )
A.x=e为函数f(x)的极大值点
B.x=e为函数f(x)的极小值点
C.为函数f(x)的极大值点
D.为函数f(x)的极小值点
解:的定义域(0,+∞),求导f′(x)=,
令f′(x)=>0,解得:0<x<e,令f′(x)=<0,解得:x>e,
∴函数在(0,e)上递增,在(e,+∞)上递减,
∴当x=e时,函数有极大值,
故选:A.
10.已知f(x)=x2+2xf'(2016)﹣2016lnx,则f′(2016)=( )
A.2015 B.﹣2015 C.2016 D.﹣2016
解:f(x)=x2+2xf'(2016)﹣2016lnx,
则f′(x)=x+2f'(2016)﹣,
则f′(2016)=2016+2f'(2016)﹣,
则f′(2016)=﹣2015,
故选:B.
11.已知点P在抛物线x2=4y上,则当点P到点Q(1,2)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
A.(2,1) B.(﹣2,1) C. D.
解:抛物线x2=4y的焦点F的坐标为F(0,1),准线方程为y=﹣1,
过点P作PN⊥l,垂足为N,连接FP,则|PN|=|FP|.
故当PQ∥y轴时,|PQ|+|PF|取得最小值|QN|=2﹣(﹣1)=3.
设点P(1,y),代入抛物线方程12=4y,解得y=,
∴P(1,).
故选:D.
12.定义在R上的函数f(x)满足:f(x)+f′(x)>1,f(0)=4,则不等式exf(x)>ex+3(其中e为自然对数的底数)的解集为( )
A.(0,+∞) B.(﹣∞,0)∪(3,+∞)
C.(﹣∞,0)∪(0,+∞) D.(3,+∞)
解:设g(x)=exf(x)﹣ex,(x∈R),
则g′(x)=exf(x)+exf′(x)﹣ex=ex[f(x)+f′(x)﹣1],
∵f(x)+f′(x)>1,
∴f(x)+f′(x)﹣1>0,
∴g′(x)>0,
∴y=g(x)在定义域上单调递增,
∵exf(x)>ex+3,
∴g(x)>3,
又∵g(0)═e0f(0)﹣e0=4﹣1=3,
∴g(x)>g(0),
∴x>0
故选:A.
二、填空题(本大题共4小题,共20.0分)
13.定积分(x+ex)dx= .
解:根据题意,= xd(x)+exd(x)=+ex=e﹣;
故答案为:e﹣.
14.已知复数z=m2(1+i)﹣m(3+6i)为纯虚数,则实数m= 3 .
解:复数z=m2(1+i)﹣m(3+6i)=(m2﹣3m)+(m2﹣6m)i为纯虚数,
∴,解得m=3.
故答案为:3.
15.已知直线y=x﹣1与椭圆交于A、B两点,则线段AB的长为 .
解:联立,得7x2﹣8x﹣8=0,
△=64+4×7×8=288>0,
设A(x1,y),B(x2,y2),则,
∴|AB|==.
故答案为:.
16.给出下列命题:
①?x∈R,x3>x2;
②?x0∈R,使sin3x0=3sinx0;
③若a<b,则;
④设等差数列{an}前n项和为Sn,若S2016﹣S1=1,则S2017>1.
其中正确命题的序号是 ②④ .
解:对于选项:①?x∈R,x3>x2;根据函数的图象,当0<x<1时,x3<x2;故错误.
②?x0∈R,当x0=0时,sin3x0=3sinx0;故正确.
③若a<b,则;当时,则;故错误.
④设等差数列{an}前n项和为Sn,若S2016﹣S1=1,整理得,
化简得2015(a1+1008d)=2015a1009=1,则,
所以=,故正确.
故答案为:②④
三、解答題(本大题共6小题,共70分)
17.求出下列函数的导数.
(1)y=extanx
(2)y=ln(4x+5)3
(3)y=x
(4)y=
(5)y=e﹣x+2(2x+1)5
解:根据题意,依次计算所给函数的导数:
(1)y=extanx,其导数y′=(ex)′tanx+ex(tanx)′=extanx+,
(2)y=ln(4x+5)3,其导数y′=
(3)y=x=x3+1+x﹣2,其导数y′=3x2﹣,
(4)y=,其导数y′=,
(5)y=e﹣x+2(2x+1)5,其导数y′=(9﹣2x)(2x+1)4e﹣x+2.
18.已知命题p:?x∈R,x2+1≥m;命题q:方程表示双曲线.
(1)若命题p为真命题,求实数m的取值范围;
(2)若命题“p∨q”为真命题,“p∧q”为假命题,求实数m的取值范围.
解:(1)对于任意x∈R,x2+1≥1,
若命题p为真命题,则(x2+1)min≥m,所以m≤1;…
(2)若命题q为真命题,则(m﹣2)(m+2)<0,所以﹣2<m<2,…
因为命题“p∨q”为真命题,“p∧q”为假命题,
则p,q至少有一个假命题,所以p,q一个为真命题,一个为假命题.…
当命题p为真命题,命题q为假命题时,,则m≤﹣2,
当命题p为假命题,命题q为真命题时,,则1<m<2,
综上,m≤﹣2或1<m<2.…
19.已知函数f(x)=x3﹣3x.
(Ⅰ)求函数f(x)在[﹣2,1]上的最大值和最小值.
(Ⅱ)过点P(2,﹣6)作曲线y=f(x)的切线,求此切线的方程.
解:(Ⅰ)f(x)=x3﹣3x,
f′(x)=3x2﹣3=3(x+1)(x﹣1),
令f′(x)>0,解得:x>1或x<﹣1,
令f′(x)<0,解得:﹣1<x<1,
故f(x)在[﹣2,﹣1)递增,在(﹣1,1]递减,
而f(﹣2)=﹣2,f(﹣1)=2,f(1)=﹣2,
∴f(x)的最小值是﹣2,
f(x)的最大值是2;
(Ⅱ)∵f′(x)=3x2﹣3,
设切点坐标为(t,t3﹣3t),
则切线方程为y﹣(t3﹣3t)=3(t2﹣1)(x﹣t),
∵切线过点P(2,﹣6),∴﹣6﹣(t3﹣3t)=3(t2﹣1)(2﹣t),
化简得t3﹣3t2=0,∴t=0或t=3.
∴切线的方程:3x+y=0或24x﹣y﹣54=0.
20.已知函数f(x)=ex﹣x﹣1(e是自然对数的底数).
(1)求证:ex≥x+1;
(2)若不等式f(x)>ax﹣1在x∈[,2]上恒成立,求正数a的取值范围.
【解答】(本小题满分12分)
证明:(1)由题意知,要证ex≥x+1,只需证f(x)=ex﹣x﹣1≥0,
求导得f′(x)=ex﹣1,当x∈(0,+∞)时,f′(x)=ex﹣1>0,
当x∈(﹣∞,0)时,f′(x)=ex﹣1<0,
∴f(x)在x∈(0,+∞)是增函数,在x∈(﹣∞,0)时是减函数,
即f(x)在x=0时取最小值f(0)=0,
∴f(x)≥f(0)=0,即f(x)=ex﹣x﹣1≥0,
∴ex≥x+1.…
(2)不等式f(x)>ax﹣1在x∈[,2]上恒成立,即ex﹣x﹣1>ax﹣1在x∈[]上恒成立,
亦即a<在x∈[]上恒成立,令g(x)=,x∈[],
以下求g(x)=在x∈[]上的最小值,
,当x∈[]时,g′(x)<0,
当x∈[]时,g′(x)>0,
∴当x∈[1,2]时,g(x)单调递减,当x∈[1,2]时,g(x)单调递增,
∴g(x)在x=1处取得最小值为g(1)=e﹣1,
∴正数a的取值范围是(0,e﹣1).…
21.点是抛物上三点,其中0<a<2,并且A、B、C三点到焦点的距离成等差数列.
(Ⅰ)求抛物线方程;
(Ⅱ)证明:.
【解答】
解:(Ⅰ)由抛物线的定义,A、B、C三点到焦点的距离分别为
依题意得 解得x2=2. 将代入y2=2px,得p=2,
所以抛物线方程为y2=4x.
(Ⅱ)因为0<a<2,所以,
?,
?,
?,
?,
?4﹣a2<4
?a2>0.
而这是显然成立的,所以成立.
22.已知函数f(x)=ln﹣ax2+x,
(1)讨论函数f(x)的极值点的个数;
(2)若f(x)有两个极值点x1,x2,证明:f(x1)+f(x2)>3﹣4ln2.
解:(1)由,
得:,
(ⅰ)a=0时,,
x∈(0,1),f′(x)<0,x∈(1,+∞),f′(x)>0,
所以x=1,f(x)取得极小值,x=1是f(x)的一个极小值点.
(ⅱ)a<0时,△=1﹣8a>0,令f′(x)=0,得
显然,x1>0,x2<0,
∴,
f(x)在x=x1取得极小值,f(x)有一个极小值点.
(ⅲ)a>0时,△=1﹣8a≤0即时,f′(x)≤0,
f(x)在(0,+∞)是减函数,f(x)无极值点.
当时,△=1﹣8a>0,令f′(x)=0,得
当x∈(0,x1)和x∈(x2,+∞)f′(x)<0,x∈(x1,x2)时,f′(x)>0,
∴f(x)在x1取得极小值,在x2取得极大值,所以f(x)有两个极值点.
综上可知:(ⅰ)a≤0时,f(x)仅有一个极值点;
(ⅱ) 当时,f(x)无极值点;
(ⅲ)当时,f(x)有两个极值点.
(2)证明:由(1)知,当且仅当a∈(0,)时,f(x)有极小值点x1和极大值点x2,
且x1,x2是方程2ax2﹣x+1=0的两根,
∴,,
=
=
=,
设,
,
∴时,g(a)是减函数,,
∴,
∴f(x1)+f(x2)>3﹣4ln2.
