人教版九年级下册数学28.2.2 应用举例 同步练习(含解析)
文档属性
| 名称 | 人教版九年级下册数学28.2.2 应用举例 同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 14:26:20 | ||
图片预览



文档简介
28.2.2 应用举例
基础闯关全练
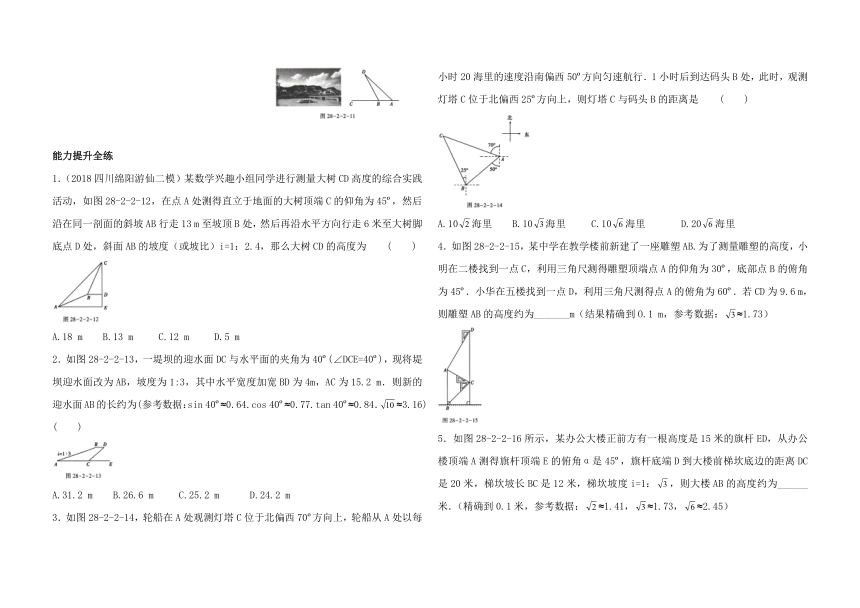
1.如图28-2-2-1,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域,为了测量受污染的圆形区域的直径,在⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30?,∠ACD=60?,则直径AD=_______米.(结果精确到1米)(参考数据:≈1.414,≈1.732)
2.如图28-2-2-2,点A、B为地球仪的南、北极点,直线AB与放置地球仪的平面交于点D,所成的角度约为67?,半径OC所在的直线与放置平面垂直,垂足为点E.DE=15 cm,AD=14 cm.求半径OA的长.(精确到0.1 cm)(参考数据:sin 67?≈0.92,cos 67?≈0.39,tan 67?≈2.36)
3.如图28-2-2-3,在小山的东侧A点有一个热气球,由于受风的影响,以30米/分钟的速度沿与地面成75?角的方向飞行.25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30?,则小山东西两侧A,B两点间的距离为 ( )
A.750m B.375m C.375m D.750m
4.如图28-2-2-4所示,某高速公路建设中需要确定隧道AB的长度.已知在离地面1500 m高度C处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60?和45?,则隧道AB的长为______.(参考数据:=1.73)
5.如图28-2-2-5,一枚运载火箭从距雷达站C处5 km的地面O处发射,当火箭到达点A,B时,在雷达站C处测得点A,B的仰角分别为34?,45?,其中点O,A,B在同一条直线上,求A,B两点间的距离.(结果精确到0.1 km)(参考数据:sin 34?=0.56,cos 34?=0.83,tan 34?=0.67)
6.如图28-2-2-6,一艘海轮位于灯塔P的南偏东45?方向,距离灯塔60 n mile的A处,它沿正北方向航行一段时间后,到达位于灯塔p的北偏东30?方向上的B处,这时,B处与灯塔P的距离为 ( )
A.60n mile B.60n mile C.30n mile D.30n mile
7.如图28-2-2-7,C地在A地的正东方向上,因有大山阻隔,由A地到C地需绕行B地.已知B地位于A地北偏东67?方向,距离A地520km,C地位于B地南偏东30?方向.若打通穿山隧道,建成两地直达高铁,求A地到C地高铁线路的长.(结果保留整数)参考数据:sin 67?≈,cos 67?≈,tan 67?≈,≈1.73)
8.如图28-2-2-8,修建抽水站时,沿着坡度为i=1:的斜坡铺设水管,若测得水管A处铅直高度为8 m.则所铺设水管AC的长度为 ( )
A.8 m B.12 m C.14 m D.16 m
9.为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE的坡度i=1:1(即DB:EB=1:1),如图28-2-2-9所示.已知AE=4米,∠EAC=130?,求水坝原来的高度BC.(参考数据:sin 50?≈0.77 ,cos 50?≈0.64,tan 50?≈1.2)
10.如图28-2-2-10,钓鱼竿AC长6m,露在水面上的鱼线BC长3m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到AC′的位置,此时露在水面上的鱼线B′C′为3m.则鱼竿转过的角度是 ( )
A.60? B.45? C.15? D.90?
11.美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一,数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图28-2-2-11,测得∠DAC=45?,∠DBC=65?.若AB=132米,求观景亭D到南滨河路AC的距离约为多少米.(结果精确到1米,参考数据:sin 65?≈0.91,cos 65?≈0.42,tan 65?≈2.14)
能力提升全练
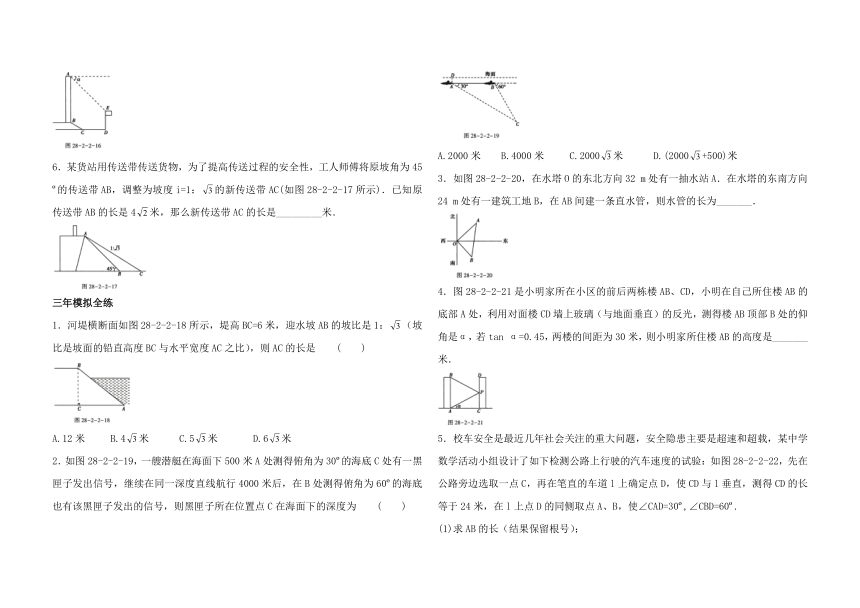
1.(2018四川绵阳游仙二模)某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图28-2-2-12,在点A处测得直立于地面的大树顶端C的仰角为45?,然后沿在同一剖面的斜坡AB行走13 m至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度为 ( )
A.18 m B.13 m C.12 m D.5 m
2.如图28-2-2-13,一堤坝的迎水面DC与水平面的夹角为40?(∠DCE=40?),现将堤坝迎水面改为AB,坡度为1:3,其中水平宽度加宽BD为4m,AC为15.2 m.则新的迎水面AB的长约为(参考数据:sin 40?≈0.64.cos 40?≈0.77.tan 40?≈0.84.≈3.16) ( )
A.31.2 m B.26.6 m C.25.2 m D.24.2 m
3.如图28-2-2-14,轮船在A处观测灯塔C位于北偏西70?方向上,轮船从A处以每小时20海里的速度沿南偏西50?方向匀速航行.1小时后到达码头B处,此时,观测灯塔C位于北偏西25?方向上,则灯塔C与码头B的距离是 ( )
A.10海里 B.10海里 C.10海里 D.20海里
4.如图28-2-2-15,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30?,底部点B的俯角为45?.小华在五楼找到一点D,利用三角尺测得点A的俯角为60?.若CD为9.6 m,则雕塑AB的高度约为_______m(结果精确到O.1 m,参考数据:≈1.73)
5.如图28-2-2-16所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45?,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:,则大楼AB的高度约为______米.(精确到0.1米,参考数据:≈1.41,≈1.73,≈2.45)
6.某货站用传送带传送货物,为了提高传送过程的安全性,工人师傅将原坡角为45?的传送带AB,调整为坡度i=1:的新传送带AC(如图28-2-2-17所示).已知原传送带AB的长是4米,那么新传送带AC的长是_________米.
三年模拟全练
1.河堤横断面如图28-2-2-18所示,堤高BC=6米,迎水坡AB的坡比是1:(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是 ( )
A.12米 B.4米 C.5米 D.6米
2.如图28-2-2-19,一艘潜艇在海面下500米A处测得俯角为30?的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60?的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为 ( )
A.2000米 B.4000米 C.2000米 D.(2000+500)米
3.如图28-2-2-20,在水塔O的东北方向32 m处有一抽水站A.在水塔的东南方向24 m处有一建筑工地B,在AB间建一条直水管,则水管的长为_______.
4.图28-2-2-21是小明家所在小区的前后两栋楼AB、CD,小明在自己所住楼AB的底部A处,利用对面楼CD墙上玻璃(与地面垂直)的反光,测得楼AB顶部B处的仰角是α,若tan α=0.45,两楼的间距为30米,则小明家所住楼AB的高度是_______米.
5.校车安全是最近几年社会关注的重大问题,安全隐患主要是超速和超载,某中学数学活动小组设计了如下检测公路上行驶的汽车速度的试验:如图28-2-2-22,先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于24米,在l上点D的同侧取点A、B,使∠CAD=30?,∠CBD=60?.
(1)求AB的长(结果保留根号);
(2)已知本路段对校车限速为45千米/时,若测得某辆校车从A到B用时2秒,则这辆校车是否超速?说明理由.(参考数据:≈1.73,≈1.41)
五年中考全练
1.如图28-2-2-23,某地修建高速公路,要从A地向B地修一条隧道(点A、B在同一水平面上).为了测量A、B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A、B两地之间的距离为 ( )
A.800sin α米 B.800tan α米 C.米 D.米
2.如图28-2-2-24,要测量小河两岸相对的两点P,A的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=100米,∠PCA=35?,则小河宽PA等于 ( )
A.100sin 35?米 B.100sin 55?米
C.100tan 35?米 D.100tan 55?米
3.如图28-2-2-25,某商店营业大厅自动扶梯AB的倾斜角为31?,AB的长约为12米,则大厅两层之间的距离BC为_______米.(结果精确到0.1米)(参考数据:sin 31?=0.515,cos 31?=0.857,tan 31?=0.601)
4.如图28-2-2-26,在一笔直的海岸线l上有相距2 km的A,B两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东60?的方向上,从B站测得船C在北偏东30?的方向上,则船C到海岸线l的距离是_______km.
5.随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起,高铁大大缩短了时空距离,改变了人们的出行方式.如图28-2-2-27,A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道,建成A,B两地的直达高铁,可以缩短从A地到B地的路程,已知:∠CAB=30?,∠CBA=45?,AC=640千米,求隧道打通后与打通前相比,从A地到B地的路程将约缩短多少千米.(参考数据:≈1.7,≈1.4)
6.某校兴趣小组借助无人飞机航拍校园,如图28-2-2-28,无人飞机从A处沿水平方向飞行至B处需8秒,在地面C处同一方向分别测得A处的仰角为750,B处仰角为30?.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
核心素养全练
1.如图28-2-2-29①②,图28-2-2-29①是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图28-2-2-29②,已知铁环的半径为25 cm,设铁环中心为O,铁环钩与铁环相切,切点为M,铁环与地面接触点为A,∠MOA=α,且sin α=,若人站立点C与点A的水平距离AC等于55 cm,则铁环钩MF的长度为 ( )
A.46 cm B.48 cm C.50 cm D.52 cm
2.图28-2-2-30是将一正方体货物沿坡面AB装进汽车货厢的平面示意图,已知长方体货厢的高度BC为2.6 m,斜坡AB的坡度为1:2.4,现把货物继续向前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,则货物的高度BD不能超过_________m.
28.2.2应用举例
1.答案 260
解析 ∠ABD=30?,∠ACD=60?,设CD=x米,则AC=2x米,AD=x米,∴tan B=,∴,解得x=150,∴AD=x=×150≈260米.
2.解析 在Rt△ODE中,DE=15(cm),∠ODE=67?,
∵cos∠ODE=,
∴OD≈≈38.46(cm),
∴OA=OD-AD=38.46-14≈24.5( cm).
答:半径OA的长约为24.5 cm.
3.A如图,过点A作AD⊥BC,垂足为D,在Rt△ACD中,∠ACD=75?-30?=45?,AC=30×25=750(m),∴AD=AC·sin 45?=375(m).在Rt△ABD中,∵∠B=30?,∴AB=2AD=750(m).故选A.
4.答案635
解析 由题意得∠AC0=30?,∠CB0=45?,
∴OA=1500tan 30?=1500×,OB=OC=1500,
∴AB=OB-OA=1500-=635(m).
5.解析 由题意,得∠AOC=90?,OC=5 km.
在Rt△AOC中,∴tan 34?=,
∴OA=OC·tan 34?=5×0.67=3.35(km).
在Rt△BOC中,∠BC0=45?,
∴OB=OC=5 km.∴AB=5-3.35=1.65≈1.7(km).
答:A,B两点间的距离约为1.7 km.
6.B过点P作PC⊥AB交AB于点C.依题意得∠APC=90?-45?=45?, ∠BPC=90?-30?=60?,AP=60 n mile,∴PC=30n mile,∴PB=2PC=60n mile.
7.解析 过点B作BD⊥AC于D.
在Rt△ABD中,AB=520,∠ABD=67?,
∴sin 67?=.
解得AD≈480,
tan 67?=,
解得BD≈200.
在Rt△CBD中,∠CBD=30?,
∴tan30?=,
解得DC≈115.3.
∴AC=AD+DC=480+115.3≈595
答:A地到C地的高铁线路的长约为595 km.
8.D∵坡度为i=1:,∴AB:BC=1:,∴AB=8,∴BC=8,∴AC==16,故所铺设水管AC的长度为16 m.故选D.
9.解析设BC=x米,∵∠CAB=180?-∠EAC=50?.
∴在Rt△ABC中,AB=(米),
∵在Rt△EBD中,i=DB:EB=1:1,∴BD=EB.
∴CD+BC=AE+AB,即2+x=4+,解得x=12.
∴BC=12米.
答:水坝原来的高度BC为12米.
10.C∵sin∠CAB=,∴∠CAB=45?.
∵sin∠C′AB′=,
∴∠C′AB′=60?.
∴∠CAC′=60?-45?=15?,鱼竿转过的角度是15?.故选C.
11.解析如图,过点D作DE⊥AC,垂足为E,
设BE=x(米),
在Rt△DEB中,tan∠DBE=,
∵∠DBC=65?.∴DE=xtan 65?.
又∵∠DAC=45?,
∴AE=DE.
∴132+x=xtan 65?,
∴x≈115.8,
∴DE≈248.
∴观景亭D到南滨河路AC的距离约为248米.
1.B如图,作BF⊥AE于F,则FE=BD=6 m,DE=BF.∵斜坡AB的坡度i=1:2.4,∴AF=2.4BF,设BF=x m,AF=2.4x m,在Rt△ABF中,由勾股定理得x?+(2.4x)?=13?,解得x=5.∴DE=BF=5 m,AF=12 m,∴AE=AF+FE=18 m,在Rt△ACE中,CE=AE·tan 45?=18×1=18 m,∴ CD=CE-DE=18-5=13 m.故选B.
2.B 如图,过B点作BF⊥AE于F,DC⊥AE于G,则BD=FG=4 m,BF=DG.∴tan∠DCE=≈0.84,∴可设CG=xm ,DG=BF=0.84xm.∴CF=CC-FG=(x-4)m,AF=AC+CF=(15.2+x)m.∵堤坝迎水面AB的坡度为1:3.∴0.84x:(15.2+x)=1:3,解得x=10,则BF=8.4 m.AF=25.2 m.∵在Rt△ABF中,∠AFB=90?,∴AB=≈26.6 m,即新的迎水面AB的长约为26.6 m.故选B.
3.C ∠CBA=25?+50?=75?.作BD⊥AC于点D.
∵∠CAB=(90?-70?)+(90?-50?)=20?+40?=60?,
则∠ABD=30?,∴∠CBD=75?-30?=45?.
在直角△ABD中,BD=AB·sin∠DAB=20sin 60?=20×(海里).
在直角△BCD中,∠CBD=45?,则BC=(海里).
4.答案6.6
解析 如图,过点C作CE⊥AB于E,过点D作DF∥CE,∵∠ADC=90?-60?=30?, ∠ACD=90?-30?=60?,∴∠CAD=90?.∵CD=9.6,∴AC=2CD=4.8.在Rt△ACE中,∵∠AEC=90?,∠ACE=30?,∴AE=AC=2.4,CE=AC·cos ∠ACE=4.8·cos 30?=,在Rt△BCE中,∵∠BCE=45?,∴BE=CE=.∴AB=AE+BE=2.4+≈6.6,即雕塑AB的高度约为6.6 m.
5.答案39.4
解析如图,延长AB交DC的延长线于H,作EG⊥AB于G,则GH=DE=15米,EG=DH,∵梯坎坡度i=l:,∴BH:CH=1:,设BH=x米,则CH=x米,在Rt△BCH中,由勾股定理得x?+(x)?=12?,解得x=6,∴BH=6米,CH=6米,∴BG=GH-BH=15-6=9(米),EG=DH=CH+CD=(6+20)米,∴∠α=450,∴AG=EG=(6+20)米,∴AB=AG+BG=6+20+9≈39.4(米).
6.答案8
解析如图,过点A作AD⊥CB,交CB的延长线于点D,∵∠ABD=45?,AB=4,∴AD=AB sin 45?=4=4,∵新传送带的坡度i=l:,∴,则DC=4,故AC==8.所以新传送带AC的长为8米.
一、选择题
1.A Rt△ABC中,BC=6米,,
∴AC=BC=6米,
∴AB==12米,故选A.
2.D如图,由C点向AB作垂线,交AB的延长线于E点,并交海面于F点.由题意知AB=4000(米),∠BAC=30?,∠EBC=60?.∴∠BCA=∠EBC-∠BAC=30?,∴∠BAC=∠BCA.∴BC=BA=4000(米).在Rt△BEC中,EC=BC·sin 60?=4000×(米).∴CF=CE+EF:(2000+500)米.故选D.
二、填空题
3.答案40 m
解析由题意可得∠AOB=90?,又∵OA=32 m,OB=24 m,
∴AB==40 m.
4.答案27
解析如图,作PE⊥AB于点E,在直角△AEP中,∠APE=∠A,则AE=PE·tan∠APE=30×0.45=13.5(米),则AB=2AE=27(米).
三、解答题
CD
5.解析(1)由题意得,在Rt△ADC中,AD=,在Rt△BDC中,BD=,所以AB=AD-BD=16,即AB的长为16米.
(2)超速.理由:因为汽车从A到曰用时2秒,所以速度约为16×1.73÷2=13.84米/秒,因为13.84×3.6=49.824,所以该校车的速度为49.824千米/时,大于45千米/时,所以此校车在AB路段超速.
一、选择题
1.D在Rt△ABC中,∵∠CAB=90?,∠B=α,AC=800米,∴tan α=,
∴AB=米.故选D.
2.C ∵PA⊥PB,PC=100米,∠PCA=35?,
∴小河宽PA=PCtan∠PCA=100tan 35?米.故选C.
二、填空题
3.答案6.2
解析在Rt△ABC中,∵∠ACB=90?, ∠A=31?,AB=12米,
∴BC=AB·sin∠A=12×0.515≈6.2(米).
即大厅两层之间的距离BC约为6.2米.
4.答案
解析过点C作CD⊥l于点D,根据题意得∠CAD=90?-60?
=30?,∠CBD=90?-30?=60?,∴∠ACB=∠CBD-∠CAD=
30?,∴∠CAB=∠ACB,∴BC=AB=2 km,在Rt△CBD中,CD=
BC·sin 60?=2× km.
三、解答题
5.解析过点C作CD⊥AB于点D,
在Rt△ADC和Rt△BCD中.
∵∠CAB=30?.∠CBA=45?,AC=64?,
∴CD=320.AD=320.
BD=CD=320,BC=320,
∴AC+BC=640+320≈1088,
∴AB=AD+BD=320+320≈864,
∴1088-864=224(千米).
答:隧道打通后与打通前相比,从A地到曰地的路程将缩短约224千米.
6.解析如图所示,过A作AD⊥BC于D,过B作BE⊥水平线于E,
∵AB∥CE,∴∠ABC=∠BCE=30?,
∵∠ACE=75?,∠BCE=30?,
∴∠ACD=45?.
在Rt△ABD中,AB=4×8=32,∠ABD=30?,
∴AD=16,BD=16√亨,
在Rt△ACD中,AD=16,∠ACD=45?,
∴CD=AD=16.
在Rt△BCE中,BC=CD+BD=16+16,∠BCE=30?,
∴BE=(16+16)=8+8.
答:这架无人飞机的飞行高度是(8+8)米.
1.C过肘作与AC平行的直线,与OA、FC分别交于H、N在Rt△OHM中,∠OHM=90?,OM=25,HM=OM·sin α=15,所以OH=20,MB=HA=25-20=5.∵铁环钩与铁环相切,∴∠MOH+∠OMH=∠OMH+∠FMN=90?.∠FMN=∠MOH=α,∴,∴FN=FM.在Rt△FMN中,∠FNM=90?,MN=BC=AC-AB=55-15=40.∵FM?=FN?+MN?,即FM?=()?+40?,解得FM=50,∴铁环钩的长度FM为50 cm.故选C.
2.答案2.4
解析如图,点D与点C重合时,B′C=BD,∠B′CB=∠CBD.=∠A.∵tan A=,∴tan∠BCB′=,设B′B=x m,b′C=2.4x m,在Rt△B′CB中,∵∠B′=90?,∴B′B?+B′C?=BC?,即x?+(2.4x)?=2.6?,解得x=1(负值舍去),∴BD=B′C=2.4 m.
基础闯关全练
1.如图28-2-2-1,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域,为了测量受污染的圆形区域的直径,在⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30?,∠ACD=60?,则直径AD=_______米.(结果精确到1米)(参考数据:≈1.414,≈1.732)
2.如图28-2-2-2,点A、B为地球仪的南、北极点,直线AB与放置地球仪的平面交于点D,所成的角度约为67?,半径OC所在的直线与放置平面垂直,垂足为点E.DE=15 cm,AD=14 cm.求半径OA的长.(精确到0.1 cm)(参考数据:sin 67?≈0.92,cos 67?≈0.39,tan 67?≈2.36)
3.如图28-2-2-3,在小山的东侧A点有一个热气球,由于受风的影响,以30米/分钟的速度沿与地面成75?角的方向飞行.25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30?,则小山东西两侧A,B两点间的距离为 ( )
A.750m B.375m C.375m D.750m
4.如图28-2-2-4所示,某高速公路建设中需要确定隧道AB的长度.已知在离地面1500 m高度C处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60?和45?,则隧道AB的长为______.(参考数据:=1.73)
5.如图28-2-2-5,一枚运载火箭从距雷达站C处5 km的地面O处发射,当火箭到达点A,B时,在雷达站C处测得点A,B的仰角分别为34?,45?,其中点O,A,B在同一条直线上,求A,B两点间的距离.(结果精确到0.1 km)(参考数据:sin 34?=0.56,cos 34?=0.83,tan 34?=0.67)
6.如图28-2-2-6,一艘海轮位于灯塔P的南偏东45?方向,距离灯塔60 n mile的A处,它沿正北方向航行一段时间后,到达位于灯塔p的北偏东30?方向上的B处,这时,B处与灯塔P的距离为 ( )
A.60n mile B.60n mile C.30n mile D.30n mile
7.如图28-2-2-7,C地在A地的正东方向上,因有大山阻隔,由A地到C地需绕行B地.已知B地位于A地北偏东67?方向,距离A地520km,C地位于B地南偏东30?方向.若打通穿山隧道,建成两地直达高铁,求A地到C地高铁线路的长.(结果保留整数)参考数据:sin 67?≈,cos 67?≈,tan 67?≈,≈1.73)
8.如图28-2-2-8,修建抽水站时,沿着坡度为i=1:的斜坡铺设水管,若测得水管A处铅直高度为8 m.则所铺设水管AC的长度为 ( )
A.8 m B.12 m C.14 m D.16 m
9.为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE的坡度i=1:1(即DB:EB=1:1),如图28-2-2-9所示.已知AE=4米,∠EAC=130?,求水坝原来的高度BC.(参考数据:sin 50?≈0.77 ,cos 50?≈0.64,tan 50?≈1.2)
10.如图28-2-2-10,钓鱼竿AC长6m,露在水面上的鱼线BC长3m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到AC′的位置,此时露在水面上的鱼线B′C′为3m.则鱼竿转过的角度是 ( )
A.60? B.45? C.15? D.90?
11.美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一,数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图28-2-2-11,测得∠DAC=45?,∠DBC=65?.若AB=132米,求观景亭D到南滨河路AC的距离约为多少米.(结果精确到1米,参考数据:sin 65?≈0.91,cos 65?≈0.42,tan 65?≈2.14)
能力提升全练
1.(2018四川绵阳游仙二模)某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图28-2-2-12,在点A处测得直立于地面的大树顶端C的仰角为45?,然后沿在同一剖面的斜坡AB行走13 m至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度为 ( )
A.18 m B.13 m C.12 m D.5 m
2.如图28-2-2-13,一堤坝的迎水面DC与水平面的夹角为40?(∠DCE=40?),现将堤坝迎水面改为AB,坡度为1:3,其中水平宽度加宽BD为4m,AC为15.2 m.则新的迎水面AB的长约为(参考数据:sin 40?≈0.64.cos 40?≈0.77.tan 40?≈0.84.≈3.16) ( )
A.31.2 m B.26.6 m C.25.2 m D.24.2 m
3.如图28-2-2-14,轮船在A处观测灯塔C位于北偏西70?方向上,轮船从A处以每小时20海里的速度沿南偏西50?方向匀速航行.1小时后到达码头B处,此时,观测灯塔C位于北偏西25?方向上,则灯塔C与码头B的距离是 ( )
A.10海里 B.10海里 C.10海里 D.20海里
4.如图28-2-2-15,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30?,底部点B的俯角为45?.小华在五楼找到一点D,利用三角尺测得点A的俯角为60?.若CD为9.6 m,则雕塑AB的高度约为_______m(结果精确到O.1 m,参考数据:≈1.73)
5.如图28-2-2-16所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45?,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:,则大楼AB的高度约为______米.(精确到0.1米,参考数据:≈1.41,≈1.73,≈2.45)
6.某货站用传送带传送货物,为了提高传送过程的安全性,工人师傅将原坡角为45?的传送带AB,调整为坡度i=1:的新传送带AC(如图28-2-2-17所示).已知原传送带AB的长是4米,那么新传送带AC的长是_________米.
三年模拟全练
1.河堤横断面如图28-2-2-18所示,堤高BC=6米,迎水坡AB的坡比是1:(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是 ( )
A.12米 B.4米 C.5米 D.6米
2.如图28-2-2-19,一艘潜艇在海面下500米A处测得俯角为30?的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60?的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为 ( )
A.2000米 B.4000米 C.2000米 D.(2000+500)米
3.如图28-2-2-20,在水塔O的东北方向32 m处有一抽水站A.在水塔的东南方向24 m处有一建筑工地B,在AB间建一条直水管,则水管的长为_______.
4.图28-2-2-21是小明家所在小区的前后两栋楼AB、CD,小明在自己所住楼AB的底部A处,利用对面楼CD墙上玻璃(与地面垂直)的反光,测得楼AB顶部B处的仰角是α,若tan α=0.45,两楼的间距为30米,则小明家所住楼AB的高度是_______米.
5.校车安全是最近几年社会关注的重大问题,安全隐患主要是超速和超载,某中学数学活动小组设计了如下检测公路上行驶的汽车速度的试验:如图28-2-2-22,先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于24米,在l上点D的同侧取点A、B,使∠CAD=30?,∠CBD=60?.
(1)求AB的长(结果保留根号);
(2)已知本路段对校车限速为45千米/时,若测得某辆校车从A到B用时2秒,则这辆校车是否超速?说明理由.(参考数据:≈1.73,≈1.41)
五年中考全练
1.如图28-2-2-23,某地修建高速公路,要从A地向B地修一条隧道(点A、B在同一水平面上).为了测量A、B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A、B两地之间的距离为 ( )
A.800sin α米 B.800tan α米 C.米 D.米
2.如图28-2-2-24,要测量小河两岸相对的两点P,A的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=100米,∠PCA=35?,则小河宽PA等于 ( )
A.100sin 35?米 B.100sin 55?米
C.100tan 35?米 D.100tan 55?米
3.如图28-2-2-25,某商店营业大厅自动扶梯AB的倾斜角为31?,AB的长约为12米,则大厅两层之间的距离BC为_______米.(结果精确到0.1米)(参考数据:sin 31?=0.515,cos 31?=0.857,tan 31?=0.601)
4.如图28-2-2-26,在一笔直的海岸线l上有相距2 km的A,B两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东60?的方向上,从B站测得船C在北偏东30?的方向上,则船C到海岸线l的距离是_______km.
5.随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起,高铁大大缩短了时空距离,改变了人们的出行方式.如图28-2-2-27,A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道,建成A,B两地的直达高铁,可以缩短从A地到B地的路程,已知:∠CAB=30?,∠CBA=45?,AC=640千米,求隧道打通后与打通前相比,从A地到B地的路程将约缩短多少千米.(参考数据:≈1.7,≈1.4)
6.某校兴趣小组借助无人飞机航拍校园,如图28-2-2-28,无人飞机从A处沿水平方向飞行至B处需8秒,在地面C处同一方向分别测得A处的仰角为750,B处仰角为30?.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
核心素养全练
1.如图28-2-2-29①②,图28-2-2-29①是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图28-2-2-29②,已知铁环的半径为25 cm,设铁环中心为O,铁环钩与铁环相切,切点为M,铁环与地面接触点为A,∠MOA=α,且sin α=,若人站立点C与点A的水平距离AC等于55 cm,则铁环钩MF的长度为 ( )
A.46 cm B.48 cm C.50 cm D.52 cm
2.图28-2-2-30是将一正方体货物沿坡面AB装进汽车货厢的平面示意图,已知长方体货厢的高度BC为2.6 m,斜坡AB的坡度为1:2.4,现把货物继续向前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,则货物的高度BD不能超过_________m.
28.2.2应用举例
1.答案 260
解析 ∠ABD=30?,∠ACD=60?,设CD=x米,则AC=2x米,AD=x米,∴tan B=,∴,解得x=150,∴AD=x=×150≈260米.
2.解析 在Rt△ODE中,DE=15(cm),∠ODE=67?,
∵cos∠ODE=,
∴OD≈≈38.46(cm),
∴OA=OD-AD=38.46-14≈24.5( cm).
答:半径OA的长约为24.5 cm.
3.A如图,过点A作AD⊥BC,垂足为D,在Rt△ACD中,∠ACD=75?-30?=45?,AC=30×25=750(m),∴AD=AC·sin 45?=375(m).在Rt△ABD中,∵∠B=30?,∴AB=2AD=750(m).故选A.
4.答案635
解析 由题意得∠AC0=30?,∠CB0=45?,
∴OA=1500tan 30?=1500×,OB=OC=1500,
∴AB=OB-OA=1500-=635(m).
5.解析 由题意,得∠AOC=90?,OC=5 km.
在Rt△AOC中,∴tan 34?=,
∴OA=OC·tan 34?=5×0.67=3.35(km).
在Rt△BOC中,∠BC0=45?,
∴OB=OC=5 km.∴AB=5-3.35=1.65≈1.7(km).
答:A,B两点间的距离约为1.7 km.
6.B过点P作PC⊥AB交AB于点C.依题意得∠APC=90?-45?=45?, ∠BPC=90?-30?=60?,AP=60 n mile,∴PC=30n mile,∴PB=2PC=60n mile.
7.解析 过点B作BD⊥AC于D.
在Rt△ABD中,AB=520,∠ABD=67?,
∴sin 67?=.
解得AD≈480,
tan 67?=,
解得BD≈200.
在Rt△CBD中,∠CBD=30?,
∴tan30?=,
解得DC≈115.3.
∴AC=AD+DC=480+115.3≈595
答:A地到C地的高铁线路的长约为595 km.
8.D∵坡度为i=1:,∴AB:BC=1:,∴AB=8,∴BC=8,∴AC==16,故所铺设水管AC的长度为16 m.故选D.
9.解析设BC=x米,∵∠CAB=180?-∠EAC=50?.
∴在Rt△ABC中,AB=(米),
∵在Rt△EBD中,i=DB:EB=1:1,∴BD=EB.
∴CD+BC=AE+AB,即2+x=4+,解得x=12.
∴BC=12米.
答:水坝原来的高度BC为12米.
10.C∵sin∠CAB=,∴∠CAB=45?.
∵sin∠C′AB′=,
∴∠C′AB′=60?.
∴∠CAC′=60?-45?=15?,鱼竿转过的角度是15?.故选C.
11.解析如图,过点D作DE⊥AC,垂足为E,
设BE=x(米),
在Rt△DEB中,tan∠DBE=,
∵∠DBC=65?.∴DE=xtan 65?.
又∵∠DAC=45?,
∴AE=DE.
∴132+x=xtan 65?,
∴x≈115.8,
∴DE≈248.
∴观景亭D到南滨河路AC的距离约为248米.
1.B如图,作BF⊥AE于F,则FE=BD=6 m,DE=BF.∵斜坡AB的坡度i=1:2.4,∴AF=2.4BF,设BF=x m,AF=2.4x m,在Rt△ABF中,由勾股定理得x?+(2.4x)?=13?,解得x=5.∴DE=BF=5 m,AF=12 m,∴AE=AF+FE=18 m,在Rt△ACE中,CE=AE·tan 45?=18×1=18 m,∴ CD=CE-DE=18-5=13 m.故选B.
2.B 如图,过B点作BF⊥AE于F,DC⊥AE于G,则BD=FG=4 m,BF=DG.∴tan∠DCE=≈0.84,∴可设CG=xm ,DG=BF=0.84xm.∴CF=CC-FG=(x-4)m,AF=AC+CF=(15.2+x)m.∵堤坝迎水面AB的坡度为1:3.∴0.84x:(15.2+x)=1:3,解得x=10,则BF=8.4 m.AF=25.2 m.∵在Rt△ABF中,∠AFB=90?,∴AB=≈26.6 m,即新的迎水面AB的长约为26.6 m.故选B.
3.C ∠CBA=25?+50?=75?.作BD⊥AC于点D.
∵∠CAB=(90?-70?)+(90?-50?)=20?+40?=60?,
则∠ABD=30?,∴∠CBD=75?-30?=45?.
在直角△ABD中,BD=AB·sin∠DAB=20sin 60?=20×(海里).
在直角△BCD中,∠CBD=45?,则BC=(海里).
4.答案6.6
解析 如图,过点C作CE⊥AB于E,过点D作DF∥CE,∵∠ADC=90?-60?=30?, ∠ACD=90?-30?=60?,∴∠CAD=90?.∵CD=9.6,∴AC=2CD=4.8.在Rt△ACE中,∵∠AEC=90?,∠ACE=30?,∴AE=AC=2.4,CE=AC·cos ∠ACE=4.8·cos 30?=,在Rt△BCE中,∵∠BCE=45?,∴BE=CE=.∴AB=AE+BE=2.4+≈6.6,即雕塑AB的高度约为6.6 m.
5.答案39.4
解析如图,延长AB交DC的延长线于H,作EG⊥AB于G,则GH=DE=15米,EG=DH,∵梯坎坡度i=l:,∴BH:CH=1:,设BH=x米,则CH=x米,在Rt△BCH中,由勾股定理得x?+(x)?=12?,解得x=6,∴BH=6米,CH=6米,∴BG=GH-BH=15-6=9(米),EG=DH=CH+CD=(6+20)米,∴∠α=450,∴AG=EG=(6+20)米,∴AB=AG+BG=6+20+9≈39.4(米).
6.答案8
解析如图,过点A作AD⊥CB,交CB的延长线于点D,∵∠ABD=45?,AB=4,∴AD=AB sin 45?=4=4,∵新传送带的坡度i=l:,∴,则DC=4,故AC==8.所以新传送带AC的长为8米.
一、选择题
1.A Rt△ABC中,BC=6米,,
∴AC=BC=6米,
∴AB==12米,故选A.
2.D如图,由C点向AB作垂线,交AB的延长线于E点,并交海面于F点.由题意知AB=4000(米),∠BAC=30?,∠EBC=60?.∴∠BCA=∠EBC-∠BAC=30?,∴∠BAC=∠BCA.∴BC=BA=4000(米).在Rt△BEC中,EC=BC·sin 60?=4000×(米).∴CF=CE+EF:(2000+500)米.故选D.
二、填空题
3.答案40 m
解析由题意可得∠AOB=90?,又∵OA=32 m,OB=24 m,
∴AB==40 m.
4.答案27
解析如图,作PE⊥AB于点E,在直角△AEP中,∠APE=∠A,则AE=PE·tan∠APE=30×0.45=13.5(米),则AB=2AE=27(米).
三、解答题
CD
5.解析(1)由题意得,在Rt△ADC中,AD=,在Rt△BDC中,BD=,所以AB=AD-BD=16,即AB的长为16米.
(2)超速.理由:因为汽车从A到曰用时2秒,所以速度约为16×1.73÷2=13.84米/秒,因为13.84×3.6=49.824,所以该校车的速度为49.824千米/时,大于45千米/时,所以此校车在AB路段超速.
一、选择题
1.D在Rt△ABC中,∵∠CAB=90?,∠B=α,AC=800米,∴tan α=,
∴AB=米.故选D.
2.C ∵PA⊥PB,PC=100米,∠PCA=35?,
∴小河宽PA=PCtan∠PCA=100tan 35?米.故选C.
二、填空题
3.答案6.2
解析在Rt△ABC中,∵∠ACB=90?, ∠A=31?,AB=12米,
∴BC=AB·sin∠A=12×0.515≈6.2(米).
即大厅两层之间的距离BC约为6.2米.
4.答案
解析过点C作CD⊥l于点D,根据题意得∠CAD=90?-60?
=30?,∠CBD=90?-30?=60?,∴∠ACB=∠CBD-∠CAD=
30?,∴∠CAB=∠ACB,∴BC=AB=2 km,在Rt△CBD中,CD=
BC·sin 60?=2× km.
三、解答题
5.解析过点C作CD⊥AB于点D,
在Rt△ADC和Rt△BCD中.
∵∠CAB=30?.∠CBA=45?,AC=64?,
∴CD=320.AD=320.
BD=CD=320,BC=320,
∴AC+BC=640+320≈1088,
∴AB=AD+BD=320+320≈864,
∴1088-864=224(千米).
答:隧道打通后与打通前相比,从A地到曰地的路程将缩短约224千米.
6.解析如图所示,过A作AD⊥BC于D,过B作BE⊥水平线于E,
∵AB∥CE,∴∠ABC=∠BCE=30?,
∵∠ACE=75?,∠BCE=30?,
∴∠ACD=45?.
在Rt△ABD中,AB=4×8=32,∠ABD=30?,
∴AD=16,BD=16√亨,
在Rt△ACD中,AD=16,∠ACD=45?,
∴CD=AD=16.
在Rt△BCE中,BC=CD+BD=16+16,∠BCE=30?,
∴BE=(16+16)=8+8.
答:这架无人飞机的飞行高度是(8+8)米.
1.C过肘作与AC平行的直线,与OA、FC分别交于H、N在Rt△OHM中,∠OHM=90?,OM=25,HM=OM·sin α=15,所以OH=20,MB=HA=25-20=5.∵铁环钩与铁环相切,∴∠MOH+∠OMH=∠OMH+∠FMN=90?.∠FMN=∠MOH=α,∴,∴FN=FM.在Rt△FMN中,∠FNM=90?,MN=BC=AC-AB=55-15=40.∵FM?=FN?+MN?,即FM?=()?+40?,解得FM=50,∴铁环钩的长度FM为50 cm.故选C.
2.答案2.4
解析如图,点D与点C重合时,B′C=BD,∠B′CB=∠CBD.=∠A.∵tan A=,∴tan∠BCB′=,设B′B=x m,b′C=2.4x m,在Rt△B′CB中,∵∠B′=90?,∴B′B?+B′C?=BC?,即x?+(2.4x)?=2.6?,解得x=1(负值舍去),∴BD=B′C=2.4 m.
