苏教版数学五年级下册 第四单元测试 提优卷(含答案)
文档属性
| 名称 | 苏教版数学五年级下册 第四单元测试 提优卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 608.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 00:00:00 | ||
图片预览

文档简介
第四单元 分数的意义和性质 测试卷
一、填空。
1.3个是( ),里面着( )个,2里面有( )个。
2.如图,白棋子的数量占黑棋子的( ),黑棋子的数量占棋子总数的( )。如果拿掉一枚黑棋子,黑棋子的数量占棋子总数的( )。如果将一枚黑棋子换成白棋子,白棋子的数量占棋子总数的( )。
3.实验小学买来8箱粉笔,每箱15盒,平均分给6个年级。每个年级分得这些粉笔的( ),每个年级分得( )箱。
4.=21÷( )=( )(填最简分数)=( )(填带分数)
5.在括号里填上合适的最简分数。
25分=( )时 85平方厘米=( )平方分米
14时=( )日 280公顷=( )平方千米
6.一本书300页,小明5天看完,平均每天看这本书的( ),第150页是这本书的( )。
7.爸爸给汽车加了30升汽油,可以行驶280千米,平均行驶1千米需要汽油( )升,平均1升汽油可以行驶( )千米。
8.x是一个大于1的自然数,在分母是x的假分数中,最小的是( );在分子是x的真分数中,最大的是( )。
二、判断。
1.分数(a、b都是非0的自然数)的分子加上a,分母加上b,分数的大小不变。 ( )
2.一根1米长的彩带,第一次用去它的,第二次用去米,这根彩带刚好用完。( )
3.分数可以分为真分数、假分数和带分数三类。 ( )
4.一个分数的分子和分母都是偶数,这个分数一定不是最简分数。 ( )
5.大于而小于的分数有无数个。 ( )
三、选择。
1.在分数中,大于的有( )个。
A.1 B.2 C.3 D.4
2.分数的分子加上9,要使分数的大小不变,分母应( )。
A.加上9 B.乘3 C.加上42 D.减去9
3.分数相比,说法正确的是( )。
A.分数大小相等,分数意义也相同
B.分数大小相等,分数意义不同
C.分数大小不等,分数意义相同
D.分数大小不等,分数意义也不同
4. 100米短跑比赛,小丁用了分钟,小惠用了分钟(a是一个大于1的自然数)。谁跑得快?( )
A.小丁 B.小惠 C.同样快 D.无法确定
5.如果是一个最简真分数,那么a有( )种不同的可能。
A.1 B.4 C.7 D.2
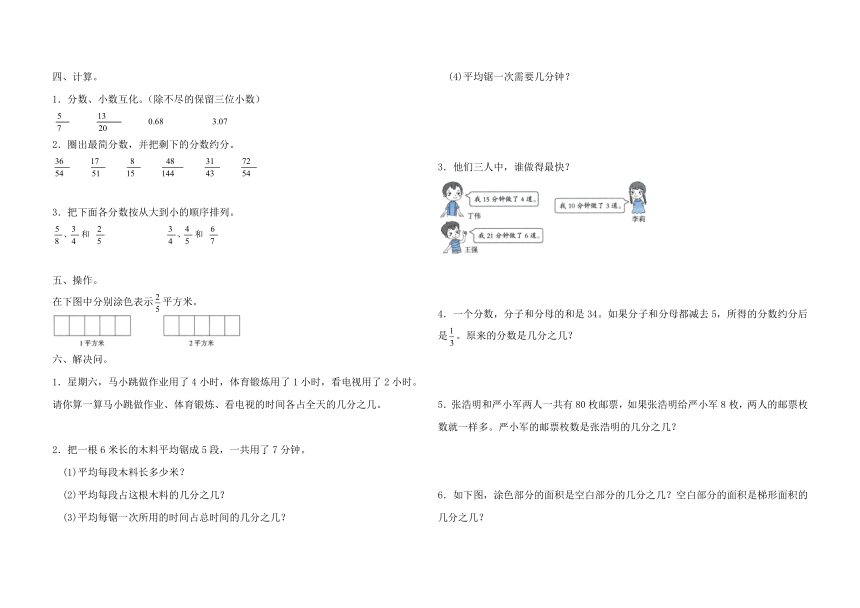
四、计算。
1.分数、小数互化。(除不尽的保留三位小数)
2.圈出最简分数,并把剩下的分数约分。
3.把下面各分数按从大到小的顺序排列。
五、操作。
在下图中分别涂色表示平方米。
六、解决问。
1.星期六,马小跳做作业用了4小时,体育锻炼用了1小时,看电视用了2小时。请你算一算马小跳做作业、体育锻炼、看电视的时间各占全天的几分之几。
2.把一根6米长的木料平均锯成5段,一共用了7分钟。
(1)平均每段木料长多少米?
(2)平均每段占这根木料的几分之几?
(3)平均每锯一次所用的时间占总时间的几分之几?
(4)平均锯一次需要几分钟?
3.他们三人中,谁做得最快?
4.一个分数,分子和分母的和是34。如果分子和分母都减去5,所得的分数约分后是。原来的分数是几分之几?
5.张浩明和严小军两人一共有80枚邮票,如果张浩明给严小军8枚,两人的邮票枚数就一样多。严小军的邮票枚数是张浩明的几分之几?
6.如下图,涂色部分的面积是空白部分的几分之几?空白部分的面积是梯形面积的几分之几?
第四单元测试(提优卷)
一、1. 4 8 2.
3. 4.15 5. 6.
7. 8.
二、1.√ 2.√ 3.× 4.√ 5.√
三、1.D 2.C 3.B 4.A 5.B
四、1.0.714 0.65
2.最简分数:
3.
五、提示:第一个涂两格,第二个涂一格。图略。
六、1.4÷24= 1÷24= 2÷24=
答:马小跳做作业、体育锻炼、看电视的时间各占全天的、、。
2.(1)6÷5=(米)
答:平均每段木料长米。
(2)1÷5=
答:平均每段占这根木料的。
(3)1÷(5-1)=
答:平均每锯一次所用的时间占总时间的。
(4)7÷(5-1)=(分)
答:平均锯一次需要分钟。
3.4÷15=(道) 6÷21=(道)
3÷10=(道) >>
答:李莉做得最快。
4. (34-5-5)÷(1+3)=6 3×6=18
6+5=11 18+5=23
答:原来的分数是。
5. 80÷2=40(枚) 40+8=48(枚)
40-8=32(枚) 32÷48=
答:严小军的邮票枚数是张浩明的。
6.解:设梯形的高为h。
涂色部分的面积:5h÷2=2.5h
空白部分的面积:8h÷2=4h
梯形的面积:(8+5)h÷2=6.5h
2.5h÷4h= 4h÷6.5h=
答:涂色部分的面积是空白部分的,空白部分的面积是梯形面积的。
一、填空。
1.3个是( ),里面着( )个,2里面有( )个。
2.如图,白棋子的数量占黑棋子的( ),黑棋子的数量占棋子总数的( )。如果拿掉一枚黑棋子,黑棋子的数量占棋子总数的( )。如果将一枚黑棋子换成白棋子,白棋子的数量占棋子总数的( )。
3.实验小学买来8箱粉笔,每箱15盒,平均分给6个年级。每个年级分得这些粉笔的( ),每个年级分得( )箱。
4.=21÷( )=( )(填最简分数)=( )(填带分数)
5.在括号里填上合适的最简分数。
25分=( )时 85平方厘米=( )平方分米
14时=( )日 280公顷=( )平方千米
6.一本书300页,小明5天看完,平均每天看这本书的( ),第150页是这本书的( )。
7.爸爸给汽车加了30升汽油,可以行驶280千米,平均行驶1千米需要汽油( )升,平均1升汽油可以行驶( )千米。
8.x是一个大于1的自然数,在分母是x的假分数中,最小的是( );在分子是x的真分数中,最大的是( )。
二、判断。
1.分数(a、b都是非0的自然数)的分子加上a,分母加上b,分数的大小不变。 ( )
2.一根1米长的彩带,第一次用去它的,第二次用去米,这根彩带刚好用完。( )
3.分数可以分为真分数、假分数和带分数三类。 ( )
4.一个分数的分子和分母都是偶数,这个分数一定不是最简分数。 ( )
5.大于而小于的分数有无数个。 ( )
三、选择。
1.在分数中,大于的有( )个。
A.1 B.2 C.3 D.4
2.分数的分子加上9,要使分数的大小不变,分母应( )。
A.加上9 B.乘3 C.加上42 D.减去9
3.分数相比,说法正确的是( )。
A.分数大小相等,分数意义也相同
B.分数大小相等,分数意义不同
C.分数大小不等,分数意义相同
D.分数大小不等,分数意义也不同
4. 100米短跑比赛,小丁用了分钟,小惠用了分钟(a是一个大于1的自然数)。谁跑得快?( )
A.小丁 B.小惠 C.同样快 D.无法确定
5.如果是一个最简真分数,那么a有( )种不同的可能。
A.1 B.4 C.7 D.2
四、计算。
1.分数、小数互化。(除不尽的保留三位小数)
2.圈出最简分数,并把剩下的分数约分。
3.把下面各分数按从大到小的顺序排列。
五、操作。
在下图中分别涂色表示平方米。
六、解决问。
1.星期六,马小跳做作业用了4小时,体育锻炼用了1小时,看电视用了2小时。请你算一算马小跳做作业、体育锻炼、看电视的时间各占全天的几分之几。
2.把一根6米长的木料平均锯成5段,一共用了7分钟。
(1)平均每段木料长多少米?
(2)平均每段占这根木料的几分之几?
(3)平均每锯一次所用的时间占总时间的几分之几?
(4)平均锯一次需要几分钟?
3.他们三人中,谁做得最快?
4.一个分数,分子和分母的和是34。如果分子和分母都减去5,所得的分数约分后是。原来的分数是几分之几?
5.张浩明和严小军两人一共有80枚邮票,如果张浩明给严小军8枚,两人的邮票枚数就一样多。严小军的邮票枚数是张浩明的几分之几?
6.如下图,涂色部分的面积是空白部分的几分之几?空白部分的面积是梯形面积的几分之几?
第四单元测试(提优卷)
一、1. 4 8 2.
3. 4.15 5. 6.
7. 8.
二、1.√ 2.√ 3.× 4.√ 5.√
三、1.D 2.C 3.B 4.A 5.B
四、1.0.714 0.65
2.最简分数:
3.
五、提示:第一个涂两格,第二个涂一格。图略。
六、1.4÷24= 1÷24= 2÷24=
答:马小跳做作业、体育锻炼、看电视的时间各占全天的、、。
2.(1)6÷5=(米)
答:平均每段木料长米。
(2)1÷5=
答:平均每段占这根木料的。
(3)1÷(5-1)=
答:平均每锯一次所用的时间占总时间的。
(4)7÷(5-1)=(分)
答:平均锯一次需要分钟。
3.4÷15=(道) 6÷21=(道)
3÷10=(道) >>
答:李莉做得最快。
4. (34-5-5)÷(1+3)=6 3×6=18
6+5=11 18+5=23
答:原来的分数是。
5. 80÷2=40(枚) 40+8=48(枚)
40-8=32(枚) 32÷48=
答:严小军的邮票枚数是张浩明的。
6.解:设梯形的高为h。
涂色部分的面积:5h÷2=2.5h
空白部分的面积:8h÷2=4h
梯形的面积:(8+5)h÷2=6.5h
2.5h÷4h= 4h÷6.5h=
答:涂色部分的面积是空白部分的,空白部分的面积是梯形面积的。
