人教版数学八年级上册:14.1.4 多项式与多项式相乘(教案)
文档属性
| 名称 | 人教版数学八年级上册:14.1.4 多项式与多项式相乘(教案) |

|
|
| 格式 | zip | ||
| 文件大小 | 120.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-17 14:05:40 | ||
图片预览

文档简介
课题名称:多项式与多项式相乘
年级学科 八年级数学 教材版本 人教版
一、教学内容分析
第14章“整式的乘法与因式分解”是继“整式的加减”之后,初中阶段对整式的第二次的研究,是进一步学习因式分解、分式方程等知识的基础,同时它在实际生活中有着广泛的应用。“多项式与多项式相乘”是本章重点内容之一,是单项式的乘法、同底数幂相乘、幂的乘方等运算法则的综合运用。本课学习多项式与多项式相乘的法则,对学生初中阶段学好必备的基础知识与基本技能、解决实际问题起到基础作用,在提高学生的运算能力方面有重要的作用。同时,对后续教学内容起到奠基作用。
二、教学目标
1、知识与技能让学生理解多项式乘以多项式的运算法则,能够按多项式乘法步骤进行简单的乘法运算.2、过程与方法经历探索多项式与多项式相乘的运算法则的推理过程,体会其运算的算理.3、情感、态度与价值观通过推理,培养学生计算能力,发展有条理的思考,逐步形成主动探索的习惯.
三、学习者特征分析
从心理特征来说,初中阶段的学生逻辑思维从经验型逐步向理论型发展,观察能力,记忆能力和想象能力也随着迅速发展。但同时,这一阶段的学生好动,注意力易分散,爱发表见解,希望得到老师的表扬,所以在教学中应抓住这些特点,一方面运用直观生动的形象,引发学生的兴趣,使他们的注意力始终集中在课堂上;另一方面,要创造条件和机会,让学生发表见解,发挥学生学习的主动性。
四、教学过程
教师活动 学生活动 设计意图
(一)复习回顾选择 学生通过平板做选择。 通过复习单项式乘以单项式的运算,为学习多项式乘以多项式法则的学习做准备。
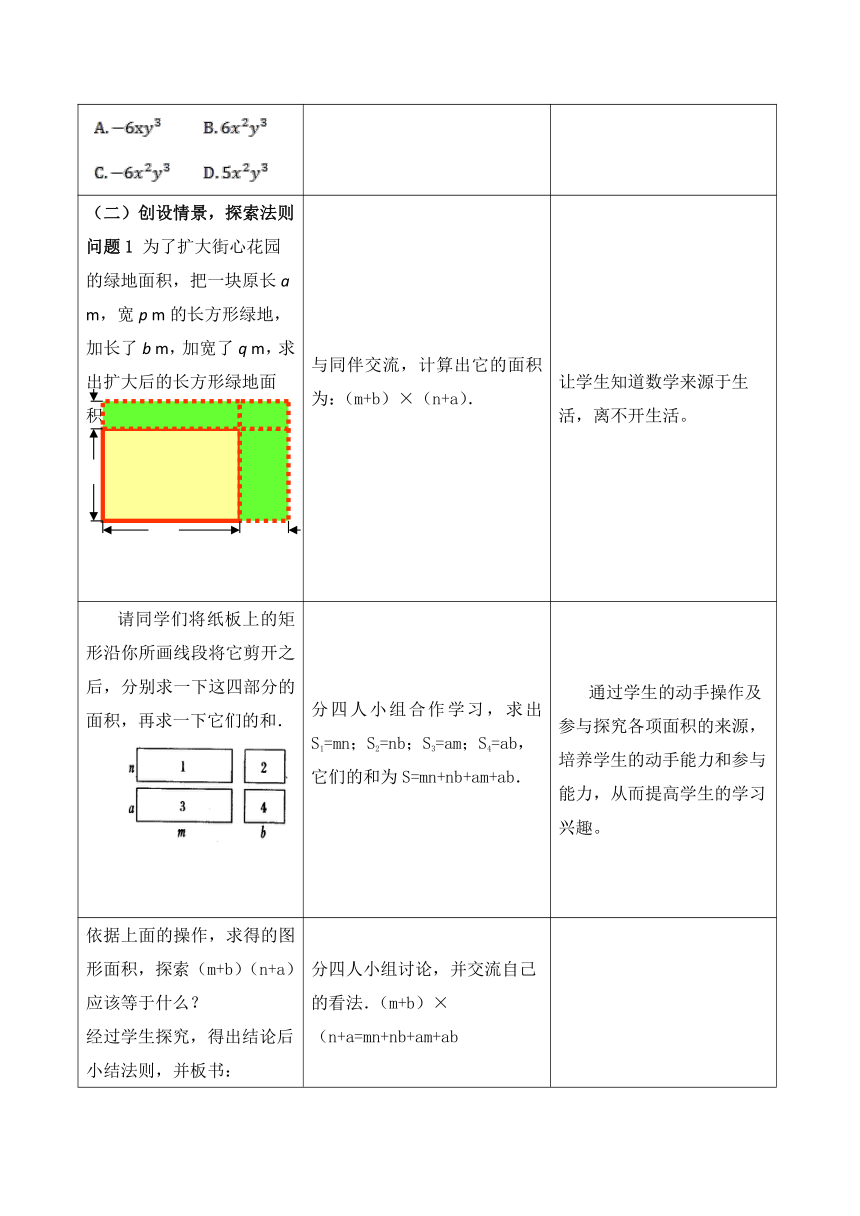
(二)创设情景,探索法则问题1 为了扩大街心花园的绿地面积,把一块原长a m,宽p m的长方形绿地,加长了b m,加宽了q m,求出扩大后的长方形绿地面积? 与同伴交流,计算出它的面积为:(m+b)×(n+a). 让学生知道数学来源于生活,离不开生活。
请同学们将纸板上的矩形沿你所画线段将它剪开之后,分别求一下这四部分的面积,再求一下它们的和. 分四人小组合作学习,求出S1=mn;S2=nb;S3=am;S4=ab,它们的和为S=mn+nb+am+ab. 通过学生的动手操作及参与探究各项面积的来源,培养学生的动手能力和参与能力,从而提高学生的学习兴趣。
依据上面的操作,求得的图形面积,探索(m+b)(n+a)应该等于什么?经过学生探究,得出结论后小结法则,并板书:=ma+mb+na+nb. 分四人小组讨论,并交流自己的看法.(m+b)×(n+a=mn+nb+am+ab
出示例6,启发学生参与到例题所设置的计算问题中去.例6 计算:(1)(3x+1)(x+2)(2)(x-8y)(x-y)(3)(x+y)( x2-xy+y2)出示例7 化简:-3x2·(xy-y2)-10x·(x2y-xy2) 参与其中,领会多项式乘法的运用方法以及注意的问题. 通过师生的讨论解题,巩固所学知识。
练习:教材102页练习1、2 全班齐练,完成后指名学生扮演,师生共同订正。 发展学生思维,巩固所学知识,释疑。
小结:1.多项式与多项式相乘,应充分结合导图中的问题来理解多项式与多项式相乘的结果,利用乘法分配律来理解(m+n)与(a+b)相乘的结果,导出多项式乘法的法则. 2.多项式与多项式相乘,第一步要先进行整理,在用一个多项式的每一项去乘另一个多项式的每一项时,要“依次”进行,不重复,不遗漏,且各个多项式中的项不能自乘,多项式是几个单项式的和,每一项都包括前面的符号,在计算时要正确确定积中各项的符号.
作业:教材103页复习巩固5
七、板书设计
14.1.4.(3)多项式与多项式相乘(a+b)(p+q)= ap+aq+bp+bq多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.注意:1、做到不重不漏(按顺序).2、注意积中每一项的符号.3、结果化为最简(合并同类项+去括号)
年级学科 八年级数学 教材版本 人教版
一、教学内容分析
第14章“整式的乘法与因式分解”是继“整式的加减”之后,初中阶段对整式的第二次的研究,是进一步学习因式分解、分式方程等知识的基础,同时它在实际生活中有着广泛的应用。“多项式与多项式相乘”是本章重点内容之一,是单项式的乘法、同底数幂相乘、幂的乘方等运算法则的综合运用。本课学习多项式与多项式相乘的法则,对学生初中阶段学好必备的基础知识与基本技能、解决实际问题起到基础作用,在提高学生的运算能力方面有重要的作用。同时,对后续教学内容起到奠基作用。
二、教学目标
1、知识与技能让学生理解多项式乘以多项式的运算法则,能够按多项式乘法步骤进行简单的乘法运算.2、过程与方法经历探索多项式与多项式相乘的运算法则的推理过程,体会其运算的算理.3、情感、态度与价值观通过推理,培养学生计算能力,发展有条理的思考,逐步形成主动探索的习惯.
三、学习者特征分析
从心理特征来说,初中阶段的学生逻辑思维从经验型逐步向理论型发展,观察能力,记忆能力和想象能力也随着迅速发展。但同时,这一阶段的学生好动,注意力易分散,爱发表见解,希望得到老师的表扬,所以在教学中应抓住这些特点,一方面运用直观生动的形象,引发学生的兴趣,使他们的注意力始终集中在课堂上;另一方面,要创造条件和机会,让学生发表见解,发挥学生学习的主动性。
四、教学过程
教师活动 学生活动 设计意图
(一)复习回顾选择 学生通过平板做选择。 通过复习单项式乘以单项式的运算,为学习多项式乘以多项式法则的学习做准备。
(二)创设情景,探索法则问题1 为了扩大街心花园的绿地面积,把一块原长a m,宽p m的长方形绿地,加长了b m,加宽了q m,求出扩大后的长方形绿地面积? 与同伴交流,计算出它的面积为:(m+b)×(n+a). 让学生知道数学来源于生活,离不开生活。
请同学们将纸板上的矩形沿你所画线段将它剪开之后,分别求一下这四部分的面积,再求一下它们的和. 分四人小组合作学习,求出S1=mn;S2=nb;S3=am;S4=ab,它们的和为S=mn+nb+am+ab. 通过学生的动手操作及参与探究各项面积的来源,培养学生的动手能力和参与能力,从而提高学生的学习兴趣。
依据上面的操作,求得的图形面积,探索(m+b)(n+a)应该等于什么?经过学生探究,得出结论后小结法则,并板书:=ma+mb+na+nb. 分四人小组讨论,并交流自己的看法.(m+b)×(n+a=mn+nb+am+ab
出示例6,启发学生参与到例题所设置的计算问题中去.例6 计算:(1)(3x+1)(x+2)(2)(x-8y)(x-y)(3)(x+y)( x2-xy+y2)出示例7 化简:-3x2·(xy-y2)-10x·(x2y-xy2) 参与其中,领会多项式乘法的运用方法以及注意的问题. 通过师生的讨论解题,巩固所学知识。
练习:教材102页练习1、2 全班齐练,完成后指名学生扮演,师生共同订正。 发展学生思维,巩固所学知识,释疑。
小结:1.多项式与多项式相乘,应充分结合导图中的问题来理解多项式与多项式相乘的结果,利用乘法分配律来理解(m+n)与(a+b)相乘的结果,导出多项式乘法的法则. 2.多项式与多项式相乘,第一步要先进行整理,在用一个多项式的每一项去乘另一个多项式的每一项时,要“依次”进行,不重复,不遗漏,且各个多项式中的项不能自乘,多项式是几个单项式的和,每一项都包括前面的符号,在计算时要正确确定积中各项的符号.
作业:教材103页复习巩固5
七、板书设计
14.1.4.(3)多项式与多项式相乘(a+b)(p+q)= ap+aq+bp+bq多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.注意:1、做到不重不漏(按顺序).2、注意积中每一项的符号.3、结果化为最简(合并同类项+去括号)
