陕西省吴起高级中学2019-2020学年高二上学期期末考试数学(理)试题 word版
文档属性
| 名称 | 陕西省吴起高级中学2019-2020学年高二上学期期末考试数学(理)试题 word版 |  | |
| 格式 | zip | ||
| 文件大小 | 261.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-16 22:10:30 | ||
图片预览
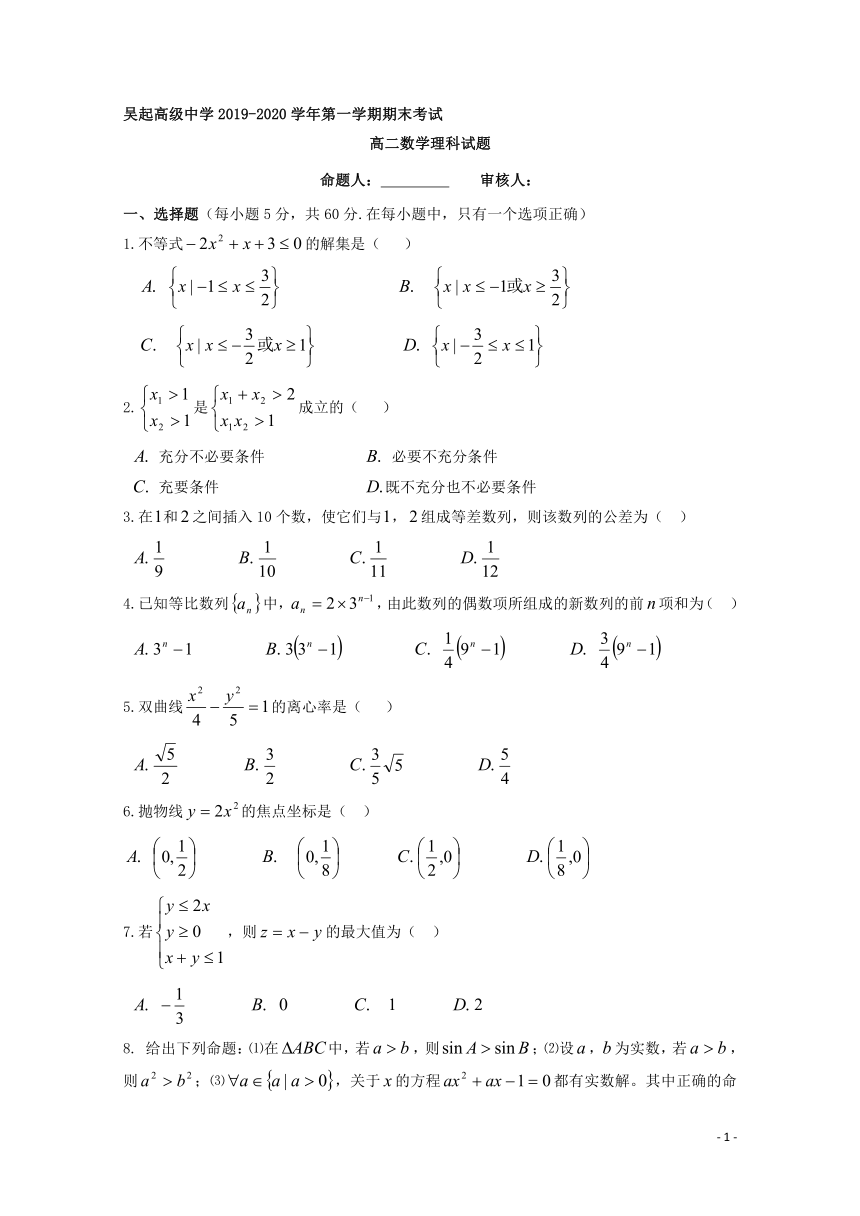



文档简介
吴起高级中学2019-2020学年第一学期期末考试
高二数学理科试题
命题人: 审核人:
一、选择题(每小题5分,共60分.在每小题中,只有一个选项正确)
1.不等式的解集是( )
2.是成立的( )
充分不必要条件 必要不充分条件
充要条件 既不充分也不必要条件
3.在和之间插入10个数,使它们与,组成等差数列,则该数列的公差为( )
4.已知等比数列中,,由此数列的偶数项所组成的新数列的前项和为( )
5.双曲线的离心率是( )
6.抛物线的焦点坐标是( )
7.若,则的最大值为( )
8. 给出下列命题:⑴在中,若,则;⑵设,为实数,若,则;⑶,关于的方程都有实数解。其中正确的命题个数是( )
9.函数的导函数( )
10. 若,,则一定有( )
A. B. C. D.
11.某运动物体的位移(单位:米)关于时间(单位:秒)的函数关系式为,
则该物体在秒时的瞬时速度为( )
A.1米/秒 B.2米/秒 C.3米/秒 D.4米/秒
12.函数的图象如图所示,则下列结论成立的是( )
A.a>0,b<0,c>0,d>0 B.a>0,b<0,c<0,d>0
C.a<0,b<0,c>0,d>0 D.a>0,b>0,c>0,d<0
二、填空题(每小题5分,共20分)
13.在中, ,,,则
14. 给出命题:,使得.写出命题的否定
15.一凸边形,各内角的度数成等差数列,公差是,最小内角是,则边数
16.椭圆上的点到点的最小距离为
三、解答题
17.(本题10分)⑴解不等式:;
⑵已知,,,求的最小值.
18.(本题12分)已知为等差数列,其前项和为,为等比数列,满足:,,.
⑴求和;
⑵设,求数列的前项和.
19. (本题12分) 在中,内角,,的对边分别为a,b,c,且满足.
⑴求角的大小;
⑵若三边a,b,c满足a+c=13,b=9,求的面积.
20. (本题12分)设命题:关于的不等式的解集为;命题:函数是上的增函数.若或非是假命题,求实数的取值范围.
21.(本题12分)已知曲线上任意一点到两个定点,的距离之和为4.
(1)求曲线的方程;
(2)设过(0,-2)的直线与曲线交于两点,且(为原点),求直线的方程.
22. (本题12分)设.
⑴当时,求在上的最大值和最小值;
⑵当时,过点作函数图像的切线,求切线方程.
吴起高级中学2019-2020学年第一学期终期考试
高二数学理科试题参考答案
命题人:
满分:150分 时间:120分钟
选择题(每小题5分,共60分.在每小题中,只有一个选项正确)
1.不等式的解集是( B )
2.是成立的( A )
充分不必要条件 必要不充分条件
充要条件 既不充分也不必要条件
3.在和之间插入10个数,使它们与,组成等差数列,则该数列的公差为( C )
4.已知等比数列中,,由此数列的偶数项所组成的新数列的前项和为( D )
5.双曲线的离心率是( B )
6.抛物线的焦点坐标是( B )
7.若,则的最大值为( C )
8. 给出下列命题:⑴在中,若,则;⑵设,为实数,若,则;⑶,关于的方程都有实数解。其中正确的命题个数是( C )
9.函数的导函数( C)
10. 若,,则一定有( D )
A. B. C. D.
11.某运动物体的位移(单位:米)关于时间(单位:秒)的函数关系式为,
则该物体在秒时的瞬时速度为( B )
A.1米/秒 B.2米/秒 C.3米/秒 D.4米/秒
12.函数的图象如图所示,则下列结论成立的是( A )
A.a>0,b<0,c>0,d>0 B.a>0,b<0, c<0,d>0
C.a<0,b<0,c>0,d>0 D.a>0,b>0,c>0,d<0
解析:∵函数f(x)的图象在y轴上的截距为正值,∴d>0.∵f′(x)=3ax2+2bx+c,且函数f(x)=ax3+bx2+cx+d在(-∞,x1)上单调递增,(x1,x2)上单调递减,(x2,+∞)上单调递增,∴f′(x)<0的解集为(x1,x2),∴a>0,又x1,x2均为正数,∴>0,->0,可得c>0,b<0.
答案:A
二、填空题(每小题5分,共20分)
13.在中, ,,,则
14. 给出命题:,使得.写出命题的否定
非:,都有
15.一凸边形,各内角的度数成等差数列,公差是,最小内角是,则边数 8
16.椭圆上的点到点的最小距离为
三、解答题
17.⑴解不等式:
⑵已知,,,求的最小值.
解:⑴∴
∴或∴原不等式的解集为
⑵,时取等号.
18.已知为等差数列,其前项和为,为等比数列,满足:,
,.⑴求和;⑵设,求数列的前项和.
解:⑴,
∴∴,∴,
⑵
∴
19. 在中,内角,,的对边分别为a,b,c,且满足.
⑴求角的大小;⑵若三边a,b,c满足a+c=13,b=9,求的面积.
解:⑴∵∴∴
∵∴∴
⑵∴
∴∴
20.设命题:关于的不等式的解集为;命题:函数是上的增函数.若或非是假命题,求实数的取值范围.
解:∵或非是假命题∴假真
∴∴∴或
∴实数的取值范围是.
21.已知曲线上任意一点到两个定点, 的距离之和为4.
(1)求曲线的方程;(2)设过(0,-2)的直线与曲线交于两点,且
(为原点),求直线的方程.
22.设,⑴当时,求在上的最大值和最小值;
⑵当时,过点作函数图像的切线,求切线方程.
高二数学理科试题
命题人: 审核人:
一、选择题(每小题5分,共60分.在每小题中,只有一个选项正确)
1.不等式的解集是( )
2.是成立的( )
充分不必要条件 必要不充分条件
充要条件 既不充分也不必要条件
3.在和之间插入10个数,使它们与,组成等差数列,则该数列的公差为( )
4.已知等比数列中,,由此数列的偶数项所组成的新数列的前项和为( )
5.双曲线的离心率是( )
6.抛物线的焦点坐标是( )
7.若,则的最大值为( )
8. 给出下列命题:⑴在中,若,则;⑵设,为实数,若,则;⑶,关于的方程都有实数解。其中正确的命题个数是( )
9.函数的导函数( )
10. 若,,则一定有( )
A. B. C. D.
11.某运动物体的位移(单位:米)关于时间(单位:秒)的函数关系式为,
则该物体在秒时的瞬时速度为( )
A.1米/秒 B.2米/秒 C.3米/秒 D.4米/秒
12.函数的图象如图所示,则下列结论成立的是( )
A.a>0,b<0,c>0,d>0 B.a>0,b<0,c<0,d>0
C.a<0,b<0,c>0,d>0 D.a>0,b>0,c>0,d<0
二、填空题(每小题5分,共20分)
13.在中, ,,,则
14. 给出命题:,使得.写出命题的否定
15.一凸边形,各内角的度数成等差数列,公差是,最小内角是,则边数
16.椭圆上的点到点的最小距离为
三、解答题
17.(本题10分)⑴解不等式:;
⑵已知,,,求的最小值.
18.(本题12分)已知为等差数列,其前项和为,为等比数列,满足:,,.
⑴求和;
⑵设,求数列的前项和.
19. (本题12分) 在中,内角,,的对边分别为a,b,c,且满足.
⑴求角的大小;
⑵若三边a,b,c满足a+c=13,b=9,求的面积.
20. (本题12分)设命题:关于的不等式的解集为;命题:函数是上的增函数.若或非是假命题,求实数的取值范围.
21.(本题12分)已知曲线上任意一点到两个定点,的距离之和为4.
(1)求曲线的方程;
(2)设过(0,-2)的直线与曲线交于两点,且(为原点),求直线的方程.
22. (本题12分)设.
⑴当时,求在上的最大值和最小值;
⑵当时,过点作函数图像的切线,求切线方程.
吴起高级中学2019-2020学年第一学期终期考试
高二数学理科试题参考答案
命题人:
满分:150分 时间:120分钟
选择题(每小题5分,共60分.在每小题中,只有一个选项正确)
1.不等式的解集是( B )
2.是成立的( A )
充分不必要条件 必要不充分条件
充要条件 既不充分也不必要条件
3.在和之间插入10个数,使它们与,组成等差数列,则该数列的公差为( C )
4.已知等比数列中,,由此数列的偶数项所组成的新数列的前项和为( D )
5.双曲线的离心率是( B )
6.抛物线的焦点坐标是( B )
7.若,则的最大值为( C )
8. 给出下列命题:⑴在中,若,则;⑵设,为实数,若,则;⑶,关于的方程都有实数解。其中正确的命题个数是( C )
9.函数的导函数( C)
10. 若,,则一定有( D )
A. B. C. D.
11.某运动物体的位移(单位:米)关于时间(单位:秒)的函数关系式为,
则该物体在秒时的瞬时速度为( B )
A.1米/秒 B.2米/秒 C.3米/秒 D.4米/秒
12.函数的图象如图所示,则下列结论成立的是( A )
A.a>0,b<0,c>0,d>0 B.a>0,b<0, c<0,d>0
C.a<0,b<0,c>0,d>0 D.a>0,b>0,c>0,d<0
解析:∵函数f(x)的图象在y轴上的截距为正值,∴d>0.∵f′(x)=3ax2+2bx+c,且函数f(x)=ax3+bx2+cx+d在(-∞,x1)上单调递增,(x1,x2)上单调递减,(x2,+∞)上单调递增,∴f′(x)<0的解集为(x1,x2),∴a>0,又x1,x2均为正数,∴>0,->0,可得c>0,b<0.
答案:A
二、填空题(每小题5分,共20分)
13.在中, ,,,则
14. 给出命题:,使得.写出命题的否定
非:,都有
15.一凸边形,各内角的度数成等差数列,公差是,最小内角是,则边数 8
16.椭圆上的点到点的最小距离为
三、解答题
17.⑴解不等式:
⑵已知,,,求的最小值.
解:⑴∴
∴或∴原不等式的解集为
⑵,时取等号.
18.已知为等差数列,其前项和为,为等比数列,满足:,
,.⑴求和;⑵设,求数列的前项和.
解:⑴,
∴∴,∴,
⑵
∴
19. 在中,内角,,的对边分别为a,b,c,且满足.
⑴求角的大小;⑵若三边a,b,c满足a+c=13,b=9,求的面积.
解:⑴∵∴∴
∵∴∴
⑵∴
∴∴
20.设命题:关于的不等式的解集为;命题:函数是上的增函数.若或非是假命题,求实数的取值范围.
解:∵或非是假命题∴假真
∴∴∴或
∴实数的取值范围是.
21.已知曲线上任意一点到两个定点, 的距离之和为4.
(1)求曲线的方程;(2)设过(0,-2)的直线与曲线交于两点,且
(为原点),求直线的方程.
22.设,⑴当时,求在上的最大值和最小值;
⑵当时,过点作函数图像的切线,求切线方程.
同课章节目录
