1.3算法案例(共50张PPT)
文档属性
| 名称 | 1.3算法案例(共50张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 931.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-17 18:39:40 | ||
图片预览









文档简介
(共50张PPT)
1.3 算法案例
方法:
新课导入
先用两个公有的质因数连续去除,一直除到所得的商是互质数为止,然后把所有的除数连乘起来。
求两个数最大公约数的方法?
除了用这种方法外还有没有其它方法?
求算出8256和6105的最大公约数
解析:
如果按照以上的方法求最大公约数,会很麻烦,而其工作量也很多。
想一想
观察用辗转相除法求8251和6105的最大公约数的过程:
第一步 用两数中较大的数除以较小的数,求得商和余数:8251=6105×1+2146
第二步 对6105和2146重复第一步是6105=2146×2+1813同理6105和2146的最大公约数也是2146和1813的最大公约数。
观察
结论: 8251和6105的公约数就是6105和2146的公约数,求8251和6105的最大公约数,只要求出6105和2146的公约数就可以了。
思考:从上述的过程你体会到了什么?
完整的过程
8251=6105×1+2146
6105=2146×2+1813
2146=1813×1+333
1813=333×5+148
333=148×2+37
148=37×4+0
显然37是148和37的最大公约数,也就是8251和6105的最大公约数
从上面的例子可以看出计算的规律是什么?
S1:用大数除以小数
S2:除数变成被除数,余数变成除数
S3:重复S1,直到余数为0
归纳
算法表示:
算法步骤!
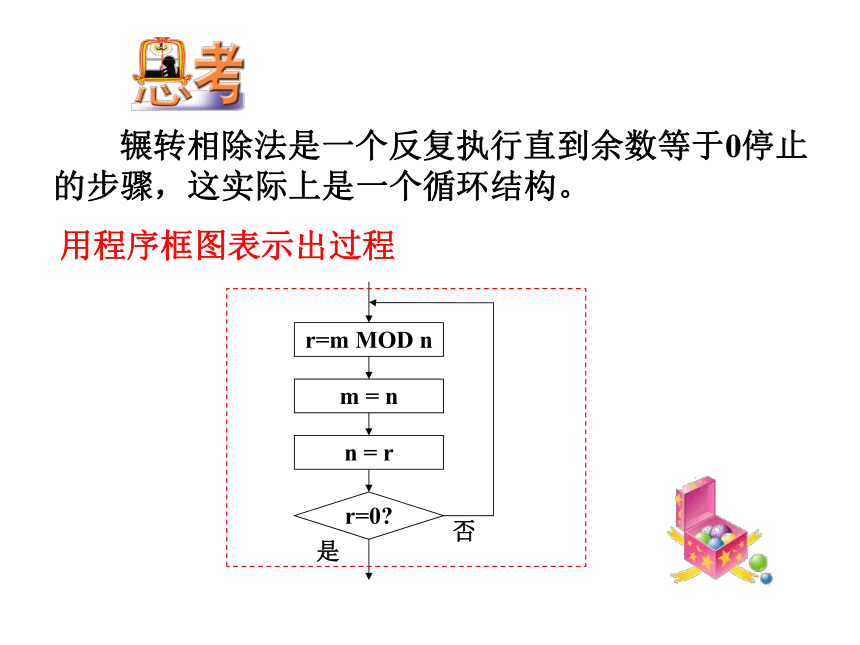
辗转相除法是一个反复执行直到余数等于0停止的步骤,这实际上是一个循环结构。
用程序框图表示出过程
r=m MOD n
m = n
n = r
r=0?
是
否
知识要点
辗转相除法(欧几里得算法) :
所谓辗转相除法,就是对于给定的两个数,用较大的数除以较小的数。若余数不为零,则将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小数除尽,则这时较小的数就是原来两个数的最大公约数。
辗转相除法算法步骤:
第一步:输入两个正整数m,n(m>n);
第二步:计算m除以n所得的余数r;
第三步:m=n,n=r;
第四步:若r=0,则m,n的最大公约数等于m;
否则转到第二步;
第五步:输出最大公约数m。
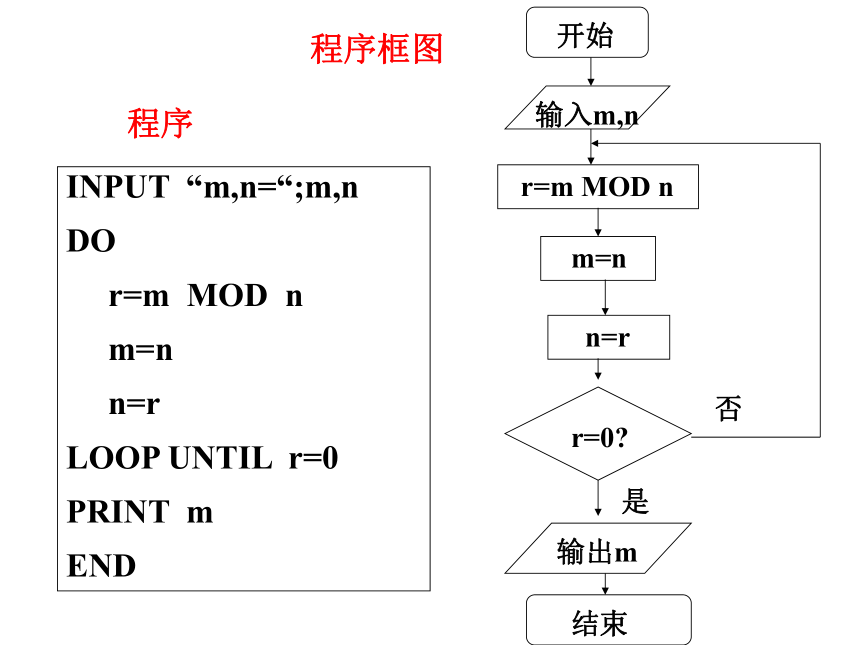
程序框图
开始
输入m,n
r=m MOD n
m=n
r=0?
是
否
n=r
输出m
结束
程序
INPUT “m,n=“;m,n
DO
r=m MOD n
m=n
n=r
LOOP UNTIL r=0
PRINT m
END
求8251和6105的最大公约数。
148=37 ×4
=37
8251=6105×1+2146
(8251,6105)
=(6105,2146)
6105=2146 ×2+1813
=(2146,1813)
2146=1813 ×1+333
=(1813,333)
1813=333 ×5+148
=(333,148)
333=148 ×2+37
=(148,37)
解:
《九章算术》——更相减损术
算理:可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之。
第一步:任意给定两个正整数;判断他们是否都是偶数。若是,则用2约简;若不是则执行第二步。
第二步:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的减数和差相等为止,则这个等数就是所求的最大公约数。
知识要点
更相减损术
所谓更相减损术,就是对于给定的两个数,用较大的数减去较小的数,然后将差和较小的数构成新的一对数,再用较大的数减去较小的数,反复执行此步骤直到差数和较小的数相等,此时相等的两数便为原来两个数的最大公约数。
更相减损术算法描述:
第一步:输入两个正整数a,b(a>b);
第二步:若a不等于b ,则执行第三步;否则转
到第五步;
第三步:把a-b的差赋予r;
第四步:如果b>r, 那么把b赋给a,把r赋给b;否
则把r赋给a,执行第二步;
第五步:输出最大公约数b。
算法步骤!
a=r
开始
输入a,b
a≠b?
是
否
输出b
结束
b=r
a=b
r=a-b
r
否
是
程序框图
程序
INPUT “a,b=“;a,b
WHILE a<>b
r=a-b
IF b>r THEN
a=b
b=r
ELSE
a=r
END IF
WEND
PRINT b
END
用更相减损术求98与63的最大公约数。
解析:由于63不是偶数,把98和63以大数减小数,并辗转相减。
按照算法步骤来求解!
= 7
所以,98和63的最大公约数等于7。
(98,63)
=(63,35)
98-63=35
?? 63-35=28
=(35,28)
35-28=7
=(28,7)
28-7=21
=(21,7)
21-7=14
=(14,7)
14-7=7
=(7,7)
解:
秦九韶简介:秦九韶 (公元1202-1261年)南宋,数学家。他在1247年(淳佑七年)着成『数书九章』十八卷.全书共81道题,分为九大类:大衍类、天时类、田域类、测望类、赋役类、钱谷类、营建类、军旅类、市易类。这是一部划时代的巨著,它总结了前人在开方中所使用的列筹方法,将其整齐而有系统地应用到高次方程的有理或无理根的求解上去,其中对「大衍求一术」(一次同余组解法)和「正负开方术」(高次方程的数值解法)等有十分深入的研究。其中的”大衍求一术”(一次同余组解法),在世界数学史上占有崇高的地位。
我们已经学过了多项式的计算,下面我们计算一下多项式
当 的值。
解析:下面分别用两种算法来求其值。
并计算每个算法所用乘法和加法的次数。
算法1:
因为f(x)=x5+x4+x3+x2+x+1
所以f(5)=55+54+53+52+5+1
=3125+625+125+25+5+1
= 3906
共做了1+2+3+4=10次乘法运算,5次加法运算。
算法2:
f(5)=55+54+53+52+5+1
=5×(54+53+52+5+1 ) +1
=5×(5×(53+52+5 +1 )+1 ) +1
=5×(5×(5×(52+5 +1) +1 ) +1 ) +1
=5×(5×(5×(5 ×(5 +1) +1 )+1)+1) +1
共做了4次乘法运算,5次加法运算。
知识要点
秦九韶算法
所谓秦九韶算法,就是求一个n次多项式的值的方法。
算法步骤:
第一步:输入多项式次数n、最高次项的系数an和x的值。
第二步:将v的值初始化为an,将i的值初始化为1。
第三步:输入i次项的系数an-i。
第四步:v=vx +an-i, i=i+1。
第五步:判断i是否小于或等于n,若是,则返回第三步;否则,输出多项式的值v。
秦九韶计算多项式的方法:
归纳
已知一个5次多项式为
用秦九韶算法求这个多项式当x=5时的值。
解:根据秦九韶算法,把多项式改写成如下形式:
按照从内到外的顺序,一次计算一次多项式,可求得当x=5时的值是17255.2。
给定一组无序数组,将其从小到大排列
{ 49,38,65,76,13,27,49 }
有什么方法吗?
想一想
直接插入排序法:
插入排序的思想就是读一个,排一个。将第1个数放入数组的第1个元素中,以后读入的数与已存入数组的数进行比较,确定它在从大到小的排列中应处的位置.将该位置以及以后的元素向后推移一个位置,将读入的新数填入空出的位置中。
冒泡排序:
依次比较相邻的两个数,把大的放前面,小的放后面。即首先比较第1个数和第2个数,大数放前,小数放后.然后比较第2个数和第3个数......直到比较最后两个数。第一趟结束,最小的一定沉到最后。重复上过程,仍从第1个数开始,到最后第2个数...... 由于在排序过程中总是大数往前,小数往后,相当气泡上升,所以叫冒泡排序。
进位制是人们为了计数和运算方便而约定的计数系统。
比如:
满二进一,就是二进制;
满十进一,就是十进制;
满十二进一,就是十二进制;
满六十进一,就是六十进制
“满几进一”就是几进制,几进制的基数就是几。
基数:
式中1处在百位,第一个3所在十位,第二个3所在个位,5和9分别处在十分位和百分位。十进制数是逢十进一的。
十进制:
例如133.59,它可用一个多项式来表示:
133.59=1*102+3*101+3*100 +5*10-1+9*10-2
我们最常用最熟悉的就是十进制数,它的数值部分是十个不同的数字符号0,1,2,3,4,5,6,7,8,9来表示的。
实际上,十进制数只是计数法中的一种,但它不是唯一记数法。除了十进制数,生产生活中还会遇到非十进制的记数制。如时间:60秒为1分,60分为1小时,它是六十进制的。两根筷子一双,两只手套为一副,它们是二进制的。
其它进制:
二进制、七进制、八进制、十二进制、十六进制……
为了区分不同的进位制,常在数的右下角标明基数,十进制一般不标注基数。
例如十进制的133.59,写成133.59(10)
七进制的13,写成13(7);二进制的10,写成10(2)
实例
一般地,若k是一个大于1的整数,那么以k
为基数的k进制可以表示为一串数字连写在一起
的形式:
总结
七进制的13,写成13(7);二进制的10,写成10(2)
例如:
其它进制数化成十进制数公式
方法
二进制:
二进制数与十进制数的转换:
提示
在电子计算机中,数是以二进制的形式表示的。二进制数每个数位只可能取两个不同的数码,0和1。
把二进制数110011(2)化为十进制数。
=51
(1)二进制数化为十进制数:
上述方法可以推广为把k进制数化为十进制数的算法。
(2)十进制数化为二进制数:
把89化为二进制数。
89
44
22
11
5
2
1
0
2
2
2
2
2
2
2
余数
1
0
1
1
1
0
0
把上式各步所得的余数
从下到上排列,
得到89=1011001(2)
除2取余法
可以推广为把十进制数化为k进制数的算法,称为除k取余法。
解:
1.辗转相除法与更相减损法:
(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0而得到,而更相减损术则以减数与差相等而得到的。
课堂小结
2.秦九韶算法计算多项式的值及程序设计;
3.数字排序法中的常见的两种排序法直接插入排序法与冒泡排序法;
4.冒泡法排序的计算机程序设计;
5.注意循环语句的使用与算法的循环次数,对算法进行改进。
1(2017年广东卷文)某篮球队6名主力队员在最近三场比赛中投进的三分球个数如下表所示:
队员i 1 2 3 4 5 6
三分球个数 a1 a2 a3 a4 a5 a6
下图(右)是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,则图中判断框应填 ,输出的s=_________ 。
(注:框图中的赋值符号“=”也可以写成“←”或“:=”)
高考链接
答案: i≤6, a1+a2+a3+· · ·+a6
解析:
顺为是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,所图中判断框应填i≤6,输出s=a1+a2+a3+· · ·+a6。
2(2019山东卷理)执行右边的程序框图,输出的T=____。
30
开始
S=0,T=0,n=0
T>S
S=S+5
n=n+2
T=T+n
输出T
结束
是
否
按照程序框图依次执行为S=5,n=2,T=2;
S=10,n=4,T=2+4=6;S=15,n=6,T=6+6=12;
S=20,n=8,T=12+8=20;S=25,n=10,T=20+10=30>S,输出T=30。
解析:
1.用更相减损术求下列两数的最大公约数:
(1)(225,135)
(2)(98,196)
(3)(72,168)
(4)(153,119)
45
98
24
17
随堂练习
2.设计利用秦九韶算法计算5次多项式
当
时的值程序和的程序框图。
解:
INPUT “a1,a2,a3,a4,a5=”;a1,a2,a3,a4,a5
INPUT “x0=”;x0
n=1
v=a5
IF n<=5 THEN
n=n+1
v=x0 +a5-n
PRINT “v=”;v
END IF
END
程序框图:
1.3 算法案例
方法:
新课导入
先用两个公有的质因数连续去除,一直除到所得的商是互质数为止,然后把所有的除数连乘起来。
求两个数最大公约数的方法?
除了用这种方法外还有没有其它方法?
求算出8256和6105的最大公约数
解析:
如果按照以上的方法求最大公约数,会很麻烦,而其工作量也很多。
想一想
观察用辗转相除法求8251和6105的最大公约数的过程:
第一步 用两数中较大的数除以较小的数,求得商和余数:8251=6105×1+2146
第二步 对6105和2146重复第一步是6105=2146×2+1813同理6105和2146的最大公约数也是2146和1813的最大公约数。
观察
结论: 8251和6105的公约数就是6105和2146的公约数,求8251和6105的最大公约数,只要求出6105和2146的公约数就可以了。
思考:从上述的过程你体会到了什么?
完整的过程
8251=6105×1+2146
6105=2146×2+1813
2146=1813×1+333
1813=333×5+148
333=148×2+37
148=37×4+0
显然37是148和37的最大公约数,也就是8251和6105的最大公约数
从上面的例子可以看出计算的规律是什么?
S1:用大数除以小数
S2:除数变成被除数,余数变成除数
S3:重复S1,直到余数为0
归纳
算法表示:
算法步骤!
辗转相除法是一个反复执行直到余数等于0停止的步骤,这实际上是一个循环结构。
用程序框图表示出过程
r=m MOD n
m = n
n = r
r=0?
是
否
知识要点
辗转相除法(欧几里得算法) :
所谓辗转相除法,就是对于给定的两个数,用较大的数除以较小的数。若余数不为零,则将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小数除尽,则这时较小的数就是原来两个数的最大公约数。
辗转相除法算法步骤:
第一步:输入两个正整数m,n(m>n);
第二步:计算m除以n所得的余数r;
第三步:m=n,n=r;
第四步:若r=0,则m,n的最大公约数等于m;
否则转到第二步;
第五步:输出最大公约数m。
程序框图
开始
输入m,n
r=m MOD n
m=n
r=0?
是
否
n=r
输出m
结束
程序
INPUT “m,n=“;m,n
DO
r=m MOD n
m=n
n=r
LOOP UNTIL r=0
PRINT m
END
求8251和6105的最大公约数。
148=37 ×4
=37
8251=6105×1+2146
(8251,6105)
=(6105,2146)
6105=2146 ×2+1813
=(2146,1813)
2146=1813 ×1+333
=(1813,333)
1813=333 ×5+148
=(333,148)
333=148 ×2+37
=(148,37)
解:
《九章算术》——更相减损术
算理:可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之。
第一步:任意给定两个正整数;判断他们是否都是偶数。若是,则用2约简;若不是则执行第二步。
第二步:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的减数和差相等为止,则这个等数就是所求的最大公约数。
知识要点
更相减损术
所谓更相减损术,就是对于给定的两个数,用较大的数减去较小的数,然后将差和较小的数构成新的一对数,再用较大的数减去较小的数,反复执行此步骤直到差数和较小的数相等,此时相等的两数便为原来两个数的最大公约数。
更相减损术算法描述:
第一步:输入两个正整数a,b(a>b);
第二步:若a不等于b ,则执行第三步;否则转
到第五步;
第三步:把a-b的差赋予r;
第四步:如果b>r, 那么把b赋给a,把r赋给b;否
则把r赋给a,执行第二步;
第五步:输出最大公约数b。
算法步骤!
a=r
开始
输入a,b
a≠b?
是
否
输出b
结束
b=r
a=b
r=a-b
r
否
是
程序框图
程序
INPUT “a,b=“;a,b
WHILE a<>b
r=a-b
IF b>r THEN
a=b
b=r
ELSE
a=r
END IF
WEND
PRINT b
END
用更相减损术求98与63的最大公约数。
解析:由于63不是偶数,把98和63以大数减小数,并辗转相减。
按照算法步骤来求解!
= 7
所以,98和63的最大公约数等于7。
(98,63)
=(63,35)
98-63=35
?? 63-35=28
=(35,28)
35-28=7
=(28,7)
28-7=21
=(21,7)
21-7=14
=(14,7)
14-7=7
=(7,7)
解:
秦九韶简介:秦九韶 (公元1202-1261年)南宋,数学家。他在1247年(淳佑七年)着成『数书九章』十八卷.全书共81道题,分为九大类:大衍类、天时类、田域类、测望类、赋役类、钱谷类、营建类、军旅类、市易类。这是一部划时代的巨著,它总结了前人在开方中所使用的列筹方法,将其整齐而有系统地应用到高次方程的有理或无理根的求解上去,其中对「大衍求一术」(一次同余组解法)和「正负开方术」(高次方程的数值解法)等有十分深入的研究。其中的”大衍求一术”(一次同余组解法),在世界数学史上占有崇高的地位。
我们已经学过了多项式的计算,下面我们计算一下多项式
当 的值。
解析:下面分别用两种算法来求其值。
并计算每个算法所用乘法和加法的次数。
算法1:
因为f(x)=x5+x4+x3+x2+x+1
所以f(5)=55+54+53+52+5+1
=3125+625+125+25+5+1
= 3906
共做了1+2+3+4=10次乘法运算,5次加法运算。
算法2:
f(5)=55+54+53+52+5+1
=5×(54+53+52+5+1 ) +1
=5×(5×(53+52+5 +1 )+1 ) +1
=5×(5×(5×(52+5 +1) +1 ) +1 ) +1
=5×(5×(5×(5 ×(5 +1) +1 )+1)+1) +1
共做了4次乘法运算,5次加法运算。
知识要点
秦九韶算法
所谓秦九韶算法,就是求一个n次多项式的值的方法。
算法步骤:
第一步:输入多项式次数n、最高次项的系数an和x的值。
第二步:将v的值初始化为an,将i的值初始化为1。
第三步:输入i次项的系数an-i。
第四步:v=vx +an-i, i=i+1。
第五步:判断i是否小于或等于n,若是,则返回第三步;否则,输出多项式的值v。
秦九韶计算多项式的方法:
归纳
已知一个5次多项式为
用秦九韶算法求这个多项式当x=5时的值。
解:根据秦九韶算法,把多项式改写成如下形式:
按照从内到外的顺序,一次计算一次多项式,可求得当x=5时的值是17255.2。
给定一组无序数组,将其从小到大排列
{ 49,38,65,76,13,27,49 }
有什么方法吗?
想一想
直接插入排序法:
插入排序的思想就是读一个,排一个。将第1个数放入数组的第1个元素中,以后读入的数与已存入数组的数进行比较,确定它在从大到小的排列中应处的位置.将该位置以及以后的元素向后推移一个位置,将读入的新数填入空出的位置中。
冒泡排序:
依次比较相邻的两个数,把大的放前面,小的放后面。即首先比较第1个数和第2个数,大数放前,小数放后.然后比较第2个数和第3个数......直到比较最后两个数。第一趟结束,最小的一定沉到最后。重复上过程,仍从第1个数开始,到最后第2个数...... 由于在排序过程中总是大数往前,小数往后,相当气泡上升,所以叫冒泡排序。
进位制是人们为了计数和运算方便而约定的计数系统。
比如:
满二进一,就是二进制;
满十进一,就是十进制;
满十二进一,就是十二进制;
满六十进一,就是六十进制
“满几进一”就是几进制,几进制的基数就是几。
基数:
式中1处在百位,第一个3所在十位,第二个3所在个位,5和9分别处在十分位和百分位。十进制数是逢十进一的。
十进制:
例如133.59,它可用一个多项式来表示:
133.59=1*102+3*101+3*100 +5*10-1+9*10-2
我们最常用最熟悉的就是十进制数,它的数值部分是十个不同的数字符号0,1,2,3,4,5,6,7,8,9来表示的。
实际上,十进制数只是计数法中的一种,但它不是唯一记数法。除了十进制数,生产生活中还会遇到非十进制的记数制。如时间:60秒为1分,60分为1小时,它是六十进制的。两根筷子一双,两只手套为一副,它们是二进制的。
其它进制:
二进制、七进制、八进制、十二进制、十六进制……
为了区分不同的进位制,常在数的右下角标明基数,十进制一般不标注基数。
例如十进制的133.59,写成133.59(10)
七进制的13,写成13(7);二进制的10,写成10(2)
实例
一般地,若k是一个大于1的整数,那么以k
为基数的k进制可以表示为一串数字连写在一起
的形式:
总结
七进制的13,写成13(7);二进制的10,写成10(2)
例如:
其它进制数化成十进制数公式
方法
二进制:
二进制数与十进制数的转换:
提示
在电子计算机中,数是以二进制的形式表示的。二进制数每个数位只可能取两个不同的数码,0和1。
把二进制数110011(2)化为十进制数。
=51
(1)二进制数化为十进制数:
上述方法可以推广为把k进制数化为十进制数的算法。
(2)十进制数化为二进制数:
把89化为二进制数。
89
44
22
11
5
2
1
0
2
2
2
2
2
2
2
余数
1
0
1
1
1
0
0
把上式各步所得的余数
从下到上排列,
得到89=1011001(2)
除2取余法
可以推广为把十进制数化为k进制数的算法,称为除k取余法。
解:
1.辗转相除法与更相减损法:
(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0而得到,而更相减损术则以减数与差相等而得到的。
课堂小结
2.秦九韶算法计算多项式的值及程序设计;
3.数字排序法中的常见的两种排序法直接插入排序法与冒泡排序法;
4.冒泡法排序的计算机程序设计;
5.注意循环语句的使用与算法的循环次数,对算法进行改进。
1(2017年广东卷文)某篮球队6名主力队员在最近三场比赛中投进的三分球个数如下表所示:
队员i 1 2 3 4 5 6
三分球个数 a1 a2 a3 a4 a5 a6
下图(右)是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,则图中判断框应填 ,输出的s=_________ 。
(注:框图中的赋值符号“=”也可以写成“←”或“:=”)
高考链接
答案: i≤6, a1+a2+a3+· · ·+a6
解析:
顺为是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,所图中判断框应填i≤6,输出s=a1+a2+a3+· · ·+a6。
2(2019山东卷理)执行右边的程序框图,输出的T=____。
30
开始
S=0,T=0,n=0
T>S
S=S+5
n=n+2
T=T+n
输出T
结束
是
否
按照程序框图依次执行为S=5,n=2,T=2;
S=10,n=4,T=2+4=6;S=15,n=6,T=6+6=12;
S=20,n=8,T=12+8=20;S=25,n=10,T=20+10=30>S,输出T=30。
解析:
1.用更相减损术求下列两数的最大公约数:
(1)(225,135)
(2)(98,196)
(3)(72,168)
(4)(153,119)
45
98
24
17
随堂练习
2.设计利用秦九韶算法计算5次多项式
当
时的值程序和的程序框图。
解:
INPUT “a1,a2,a3,a4,a5=”;a1,a2,a3,a4,a5
INPUT “x0=”;x0
n=1
v=a5
IF n<=5 THEN
n=n+1
v=x0 +a5-n
PRINT “v=”;v
END IF
END
程序框图:
