北师大版数学八下1.1.3等腰三角形的判定及反证法课件(23张ppt)
文档属性
| 名称 | 北师大版数学八下1.1.3等腰三角形的判定及反证法课件(23张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 630.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-17 16:53:53 | ||
图片预览



文档简介
(共23张PPT)
第3课时 等腰三角形的判定及反证法
北师版八年级数学下册
等腰三角形性质定理的内容是什么?
等腰三角形的两个底角相等.
我们把等腰三角形的性质定理的条件和结论反过来还成立吗?
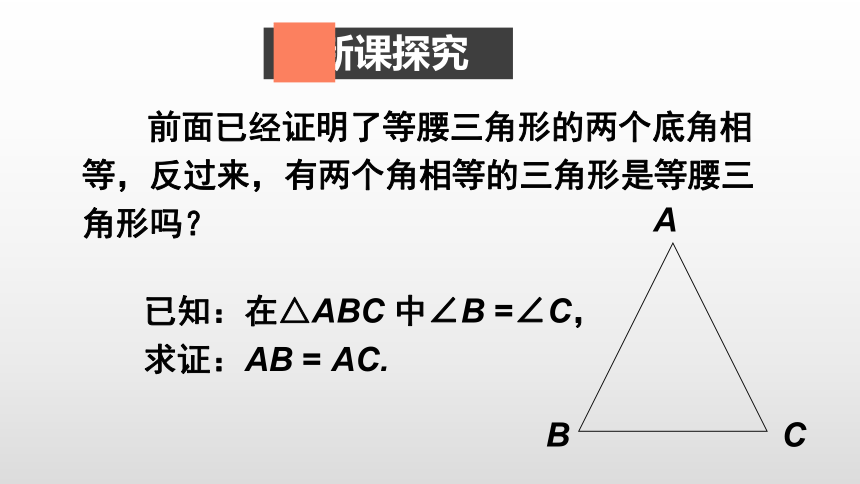
前面已经证明了等腰三角形的两个底角相等,反过来,有两个角相等的三角形是等腰三角形吗?
已知:在△ABC 中∠B =∠C,
求证:AB = AC.
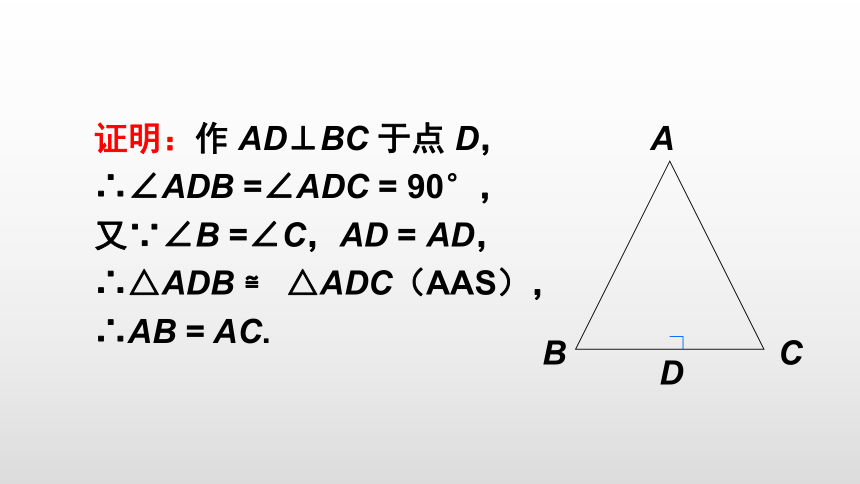
证明:作 AD⊥BC 于点 D,
∴∠ADB =∠ADC = 90°,
又∵∠B =∠C,AD = AD,
∴△ADB ≌ △ADC(AAS),
∴AB = AC.
D
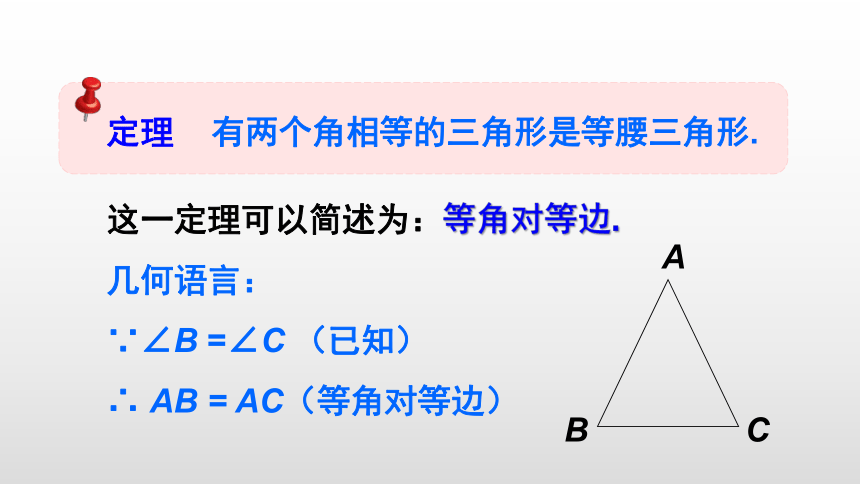
这一定理可以简述为:等角对等边.
几何语言:
∵∠B =∠C (已知)
∴ AB = AC(等角对等边)
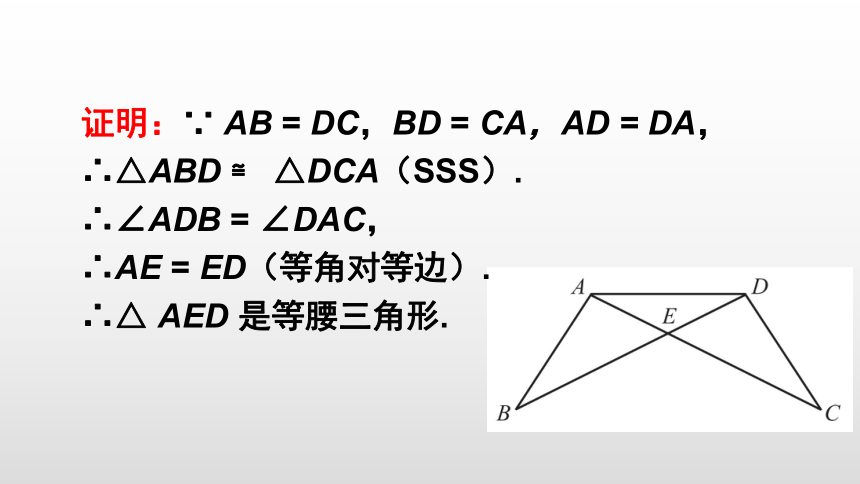
例 2 已知:如图,AB = DC,BD = CA,BD 与 CA 相交于点 E.求证:△AED 是等腰三角形.
证明:∵ AB = DC,BD = CA,AD = DA,
∴△ABD ≌ △DCA(SSS).
∴∠ADB = ∠DAC,
∴AE = ED(等角对等边).
∴△ AED 是等腰三角形.
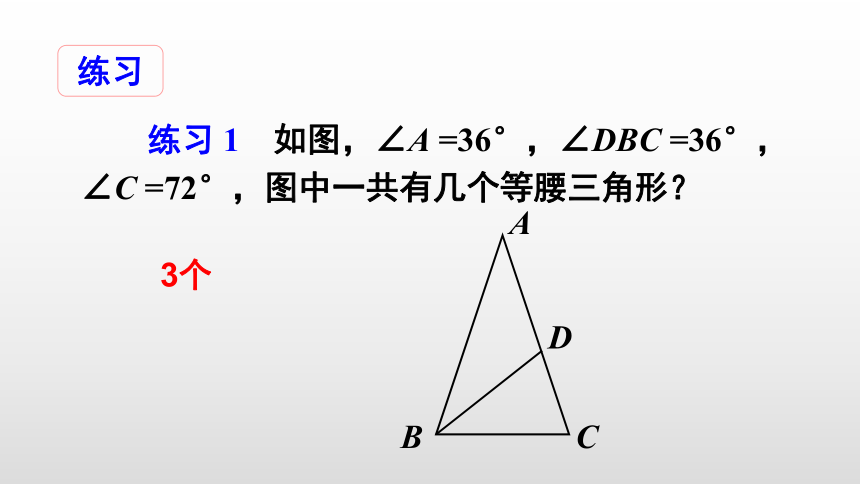
练习 1 如图,∠A =36°,∠DBC =36°,∠C =72°,图中一共有几个等腰三角形?
练习
3个
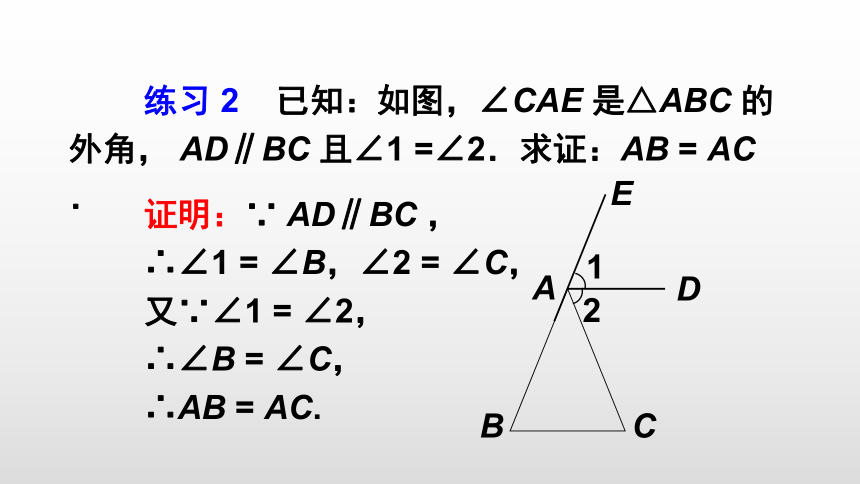
练习 2 已知:如图,∠CAE 是△ABC 的外角, AD∥BC 且∠1 =∠2.求证:AB = AC.
证明:∵ AD∥BC ,
∴∠1 = ∠B,∠2 = ∠C,
又∵∠1 = ∠2,
∴∠B = ∠C,
∴AB = AC.
小明认为,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等. 你认为这个结论成立吗?如果成立,你能证明它吗?
如图,在△ABC 中,已知
∠B ≠∠C,此时 AB 与 AC 要么相等,要么不相等.
假设 AB = AC,那么根据“等边对等角”定理可得∠C =∠B,这与已知条件∠B ≠∠C 相矛盾,因此 AB ≠ AC.
反证法:先假设命题的结论不成立,然后推导出与定义、基本事实或已知条件相矛盾的结果,从而证明命题的结论一定成立.我们把它叫做反证法.
例 3 用反证法证明:一个三角形中不能有两个角是直角.
已知:△ABC.
求证:∠A,∠B,∠C 中不能有两个角是直角.
证明:假设∠A,∠B,∠C 中有两个角是直角,不妨设∠A和∠B 是直角,即∠A = 90°,
∠B = 90°.
于是∠A +∠B +∠C = 180°+∠C >180°.
这与三角形内角和定理相矛盾,因此“∠A和∠B 是直角”的假设不成立.
所以,一个三角形中不能有两个角是直角.
1. 下列两个图形是否是等腰三角形?
是
是
2. 如图,在△ABC 中,BD 平分∠ABC,交AC 于点 D,过点 D 作 BC 的平行线,交 AB 于点E,请判断△BDE 的形状,并说明理由.
解:△BDE 是等腰三角形.
∵ BD 平分∠ABC,
∴∠ABD = ∠DBC,
又∵DE∥BC,
∴∠DBC = ∠EDB,
∴∠ABD =∠EDB,
∴△BDE 是等腰三角形.
3. 如图,上午 10 时,一条船从 A 处出发以 20 海里每小时的速度向正北航行,中午 12 时到达 B 处,从 A、B 望灯塔 C,测∠NAC = 40°,∠NBC = 80°,求从 B 处到灯塔 C 的距离.
解:∠C = ∠CBN – ∠A = 80°– 40°= 40°,
∴∠C = ∠A,∴AB = BC,
AB = 20×(12 – 10)= 40(海里),
∴BC = 40 海里
4. 求证:在一个三角形中,至少有一个内角小于或等于 60°.
证明:假设结论不成立,
即:∠A___60°,∠B ___60°,∠C ___60°,
则∠A +∠B +∠C >180 °.
这与_____________________相矛盾.
所以______不成立,所求证的结论成立.
>
>
>
三角形内角和等于180°
假设
证明:假设这五个数是a1,a2,a3,a4,a5全部小于 ,那么这五个数的和 a1 + a2 + a3 + a4 + a5 就小于 1.这与已知这五个数的和等于 1 相矛盾.因此假设不成立,原命题成立,即这五个数中至少有一个大于或等于 .
今天你学到了什么?
1. 等腰三角形的判定定理:等角对等边.
2. 会运用等腰三角形的性质和判定进行计算和证明.
1.从教材习题中选取;
2.完成练习册本课时的习题.
第3课时 等腰三角形的判定及反证法
北师版八年级数学下册
等腰三角形性质定理的内容是什么?
等腰三角形的两个底角相等.
我们把等腰三角形的性质定理的条件和结论反过来还成立吗?
前面已经证明了等腰三角形的两个底角相等,反过来,有两个角相等的三角形是等腰三角形吗?
已知:在△ABC 中∠B =∠C,
求证:AB = AC.
证明:作 AD⊥BC 于点 D,
∴∠ADB =∠ADC = 90°,
又∵∠B =∠C,AD = AD,
∴△ADB ≌ △ADC(AAS),
∴AB = AC.
D
这一定理可以简述为:等角对等边.
几何语言:
∵∠B =∠C (已知)
∴ AB = AC(等角对等边)
例 2 已知:如图,AB = DC,BD = CA,BD 与 CA 相交于点 E.求证:△AED 是等腰三角形.
证明:∵ AB = DC,BD = CA,AD = DA,
∴△ABD ≌ △DCA(SSS).
∴∠ADB = ∠DAC,
∴AE = ED(等角对等边).
∴△ AED 是等腰三角形.
练习 1 如图,∠A =36°,∠DBC =36°,∠C =72°,图中一共有几个等腰三角形?
练习
3个
练习 2 已知:如图,∠CAE 是△ABC 的外角, AD∥BC 且∠1 =∠2.求证:AB = AC.
证明:∵ AD∥BC ,
∴∠1 = ∠B,∠2 = ∠C,
又∵∠1 = ∠2,
∴∠B = ∠C,
∴AB = AC.
小明认为,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等. 你认为这个结论成立吗?如果成立,你能证明它吗?
如图,在△ABC 中,已知
∠B ≠∠C,此时 AB 与 AC 要么相等,要么不相等.
假设 AB = AC,那么根据“等边对等角”定理可得∠C =∠B,这与已知条件∠B ≠∠C 相矛盾,因此 AB ≠ AC.
反证法:先假设命题的结论不成立,然后推导出与定义、基本事实或已知条件相矛盾的结果,从而证明命题的结论一定成立.我们把它叫做反证法.
例 3 用反证法证明:一个三角形中不能有两个角是直角.
已知:△ABC.
求证:∠A,∠B,∠C 中不能有两个角是直角.
证明:假设∠A,∠B,∠C 中有两个角是直角,不妨设∠A和∠B 是直角,即∠A = 90°,
∠B = 90°.
于是∠A +∠B +∠C = 180°+∠C >180°.
这与三角形内角和定理相矛盾,因此“∠A和∠B 是直角”的假设不成立.
所以,一个三角形中不能有两个角是直角.
1. 下列两个图形是否是等腰三角形?
是
是
2. 如图,在△ABC 中,BD 平分∠ABC,交AC 于点 D,过点 D 作 BC 的平行线,交 AB 于点E,请判断△BDE 的形状,并说明理由.
解:△BDE 是等腰三角形.
∵ BD 平分∠ABC,
∴∠ABD = ∠DBC,
又∵DE∥BC,
∴∠DBC = ∠EDB,
∴∠ABD =∠EDB,
∴△BDE 是等腰三角形.
3. 如图,上午 10 时,一条船从 A 处出发以 20 海里每小时的速度向正北航行,中午 12 时到达 B 处,从 A、B 望灯塔 C,测∠NAC = 40°,∠NBC = 80°,求从 B 处到灯塔 C 的距离.
解:∠C = ∠CBN – ∠A = 80°– 40°= 40°,
∴∠C = ∠A,∴AB = BC,
AB = 20×(12 – 10)= 40(海里),
∴BC = 40 海里
4. 求证:在一个三角形中,至少有一个内角小于或等于 60°.
证明:假设结论不成立,
即:∠A___60°,∠B ___60°,∠C ___60°,
则∠A +∠B +∠C >180 °.
这与_____________________相矛盾.
所以______不成立,所求证的结论成立.
>
>
>
三角形内角和等于180°
假设
证明:假设这五个数是a1,a2,a3,a4,a5全部小于 ,那么这五个数的和 a1 + a2 + a3 + a4 + a5 就小于 1.这与已知这五个数的和等于 1 相矛盾.因此假设不成立,原命题成立,即这五个数中至少有一个大于或等于 .
今天你学到了什么?
1. 等腰三角形的判定定理:等角对等边.
2. 会运用等腰三角形的性质和判定进行计算和证明.
1.从教材习题中选取;
2.完成练习册本课时的习题.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
