人教版数学八年级上册14.2.2-完全平方公式课件(30张PPT)
文档属性
| 名称 | 人教版数学八年级上册14.2.2-完全平方公式课件(30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 222.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-18 10:25:27 | ||
图片预览









文档简介
(共30张PPT)
14.2.2 完全平方公式
第十四章 整式的乘法与因式分解
问题
高菲同学做作业时,把一滴墨水滴在一道数学题上,题目变成了x2■ x+1,看不清x前面的数字是什么,只知道这个二次三项式能写成一个整式的平方,急得她抓耳挠腮,你能帮助她吗?
学 习 新 知
计算(x+a)(x+b).
一、公式的推导
小活动
解:(x+a)(x+b)
=x2+bx+ax+ab
=x2+(a+b)x+ab
思考
1.在(x+a)(x+b)中,若a=b,那么上述式子将会成为怎样的式子?计算结果是什么?
变为(x+a)(x+a),计算结果是
x 2+2ax+a2,即(a+b)2=a2+2ab+b2.
思考
2.这个公式的左边和右边各有什么特点?
3.(a+b)2 =a 2 +b 2对吗?为什么?
两数和的平方,结果应该是三项式.
思考
4.你会用(a+b)2 =a 2 +2ab+b 2
计算(a-b)2吗?
将“-b”看作一个数,将(a-b)2化为[a+(-b)]2=a2+2a×(-b)+(-b)2
=a2-2ab+b2.
(a-b)2=a2 -2ab+b2
乘法公式
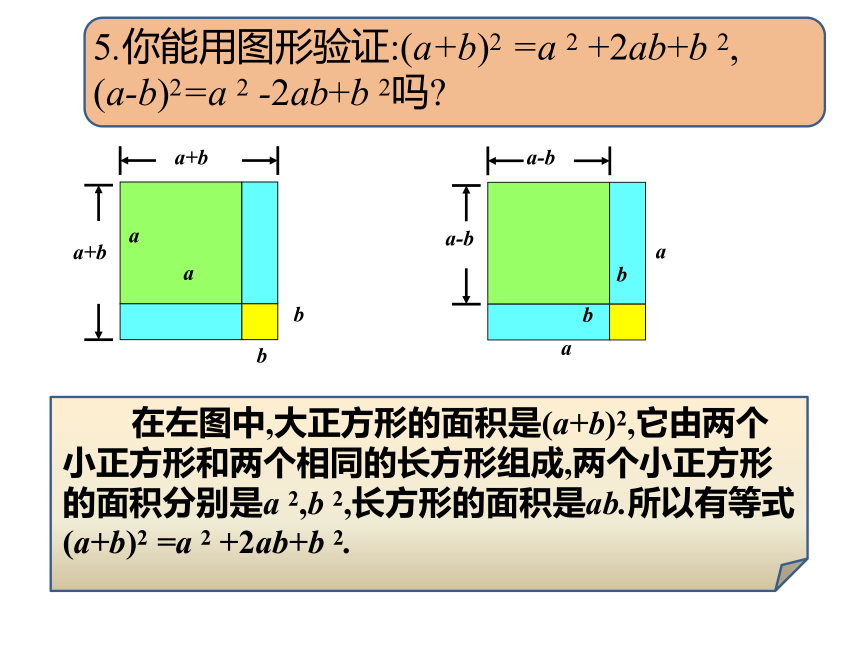
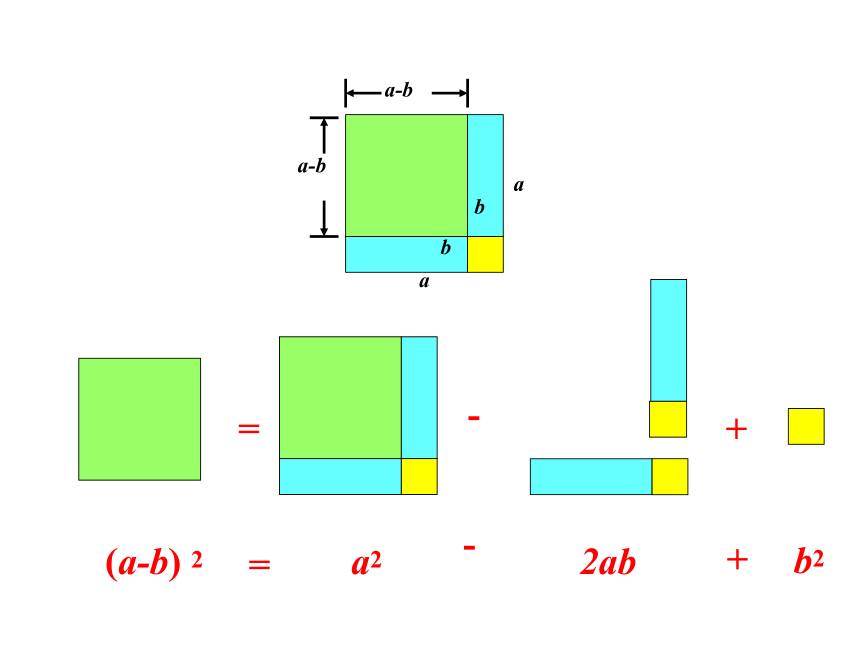
5.你能用图形验证:(a+b)2 =a 2 +2ab+b 2,
(a-b)2=a 2 -2ab+b 2吗?
在左图中,大正方形的面积是(a+b)2,它由两个小正方形和两个相同的长方形组成,两个小正方形的面积分别是a 2,b 2,长方形的面积是ab.所以有等式(a+b)2 =a 2 +2ab+b 2.
a+b
a+b
a
b
a
b
a-b
a-b
a
a
b
b
a+b
a+b
a
b
a
b
=
(a+b) 2
=
a2
+
2ab
+
+
b2
+
a-b
a-b
a
a
b
b
=
(a-b) 2
=
a2
-
2ab
-
+
b2
+
思考
6.比较(a+b)2=a 2+2ab+b 2及(a-b)2
=a 2 -2ab+b 2这两个公式.它们有什么不同?有什么联系?
(a+b)2 =a 2 +2ab+b 2
两数和的平方,等于它们的平方和加上这两数积的2倍.
(1)运用完全平方公式的关
键在于明确公式的特征:公式的
左边是两数和(或差)的平方,公
式的右边是一个三项式,是左
边两数的平方和加上(或减去)
左边两数积的2倍.
注意!
(2)①公式中字母的含义:公式中
字母a和b可以是具体的数,也可以
是整式(单项式或多项式).②利用
完全平方公式计算多项式的乘法,
最容易漏写2ab项,实际运算中要
特别注意.③完全平方公式与平方
差公式联合使用,要严格分清公式
的各自特点,以防混淆.
(3)逆用完全平方公式为:
a2 +2ab+b2=(a+b)2 ,
a2-2ab+b2=(a-b)2,把三项式
写成了积的形式,这是后面要
学习的因式分解.
例1 运用完全平方公式计算.
(1)(4m+n)2;
解:(1)(4m+n)2=(4m)2+2·(4m)·n+n2
=16m2 +8mn+n2.
例2 运用完全平方公式计算.
(1)1022 ; (2)992 .
解答
(2)992=(100-1)2
=1002 -2×100×1+12
=10000-200+1=9801.
(1)1022=(100+2)2
=1002 +2×100×2+22
=10000+400+4=10404.
党员两学一做自查自纠报告范文
“两学一做”自查报告
“两学一做”自查报告
红崖子沟心学校党支部
(20XX年3月28日)
根据互助县教育局《关于在教育系统党员开展“学党章党规、学系列讲话,做合格党员”学习教育活动的通知》互教委[2016]16号文件精神,我校结合实际,积极开展“两学一做”专题教育活动,并从以下几个方面进行了自查,现将我校自查报告结果简要汇报如下,不妥之处,敬请指正。
一、党员教师如何以习近平系列讲话指导教育教学工作 深入学习贯彻讲话精神,是在思想上政治上行动上同以习近平同志为总书记的党央保持高度一致的迫切需要。学习好、贯彻好讲话精神,对于促进党员教师进一步凝聚发展共识、明确改革方向,增强教育改革的活力和发展的动力,推进教育事业科学发展,努力办好人民满意的教育,具有十分重要的意义。为此,在专题学习讨论会上,我校党支部书记靳永录就面向全体学生,如何促进学生全面发展和主动发展
是素质教育的核心理念这一问题做了严格要求。首先,从全面贯彻党的教育方针,全面提高教育教学质量入手,进一步明确教师职责,扎实开展教学工作。其次,学校通过讲座、学习讨论等形式转变教师的思想认识,提高教师实
讨论
现有下图所示三种规格的卡片各若干张,请你根据二次三项式a2 +2ab+b2,选取相应种类和数量的卡片,尝试拼成一个正方形,并讨论该正方形的代数意义.
思考、讨论
(a+b)2与(-a-b)2相等吗?(a-b)2与(b-a)2相等吗?(a-b)2与a 2-b 2相等吗?为什么?
运用乘法公式计算,有时要在式子中添括号,在第二章中,我们学过去括号法则,即a+(b+c)=a+b+c;a-(b+c)=a-b-c.
反过来,就得到添括号法则:a+b+c=a+(b+c);a-b-c=a-(b+c).
添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号.
说明
(1)添括号法则与去括号法则是一致的,添括号正确与否,可用去括号进行检验.
(2)添括号时,如果括号前面是负号,那么括到括号里的各项都改变符号,不能只改变部分项的符号.
知识拓展
解:(1)(x+2y-3)(x-2y+3)=[x+(2y-3)][x-(2y-3)]
=x2 -(2y-3)2=x2-(4y2 -12y+9)=x2-4y2+12y-9.
(2)(a+b+c)2=[(a+b)+c]2=(a+b)2+2(a+b)c+c2
=a2 +2ab+b2 +2ac+2bc+c2
=a2 +b2 +c2 +2ab+2ac+2bc.
例题示范
例3.运用乘法公式计算.
(x+2y-3)(x-2y+3);
(a+b+c)2.
一些本来不是二项式的式子的平方也可以利用完全平方公式来计算,关键是使其转化为二项式的平方,如计算(a+b+c)2,可以把这个代数式转化为[a+(b+c)]2或[(a+b)+c]2,把b+c或a+b看做是一个整体(一个字母),也可以把这个式子转化为[(a+c)+b]2.实际操作时要看怎样做最有利于计算.
完全平方公式是进行整式乘法的重要工具,它的结构形式具有对称性,两个公式都叫做完全平方公式,前面的一个叫做和的完全平方公式,后面的一个叫做差的完全平方公式.判断一个式子能不能用完全平方公式展开,主要看它的结构形式是否符合公式要求,习惯上把(a±b)2 中的a叫做前项,b叫做后项,记忆时巧记为“首平方,末平方,首末两倍中间放”.
知识小结
2.添括号
添括号时,如果括号前面是正号,
括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号.
应用时,主要关注两点:一是关注括号前面的符号是正号还是负号;二是对
照添括号前和后符号该不该改变.
3.运用完全平方公式还应注意以下几点:
①切勿把完全平方公式与公式(ab)2 =a2b2相混淆,或随意写成(a+b)2 =a2 +b2;
②切勿把“乘积项”2ab中的2丢掉;
③计算时,要先观察题目特点,看是否符合公式的条件,若不符合,应先变形为符合公式的形式,再利用公式进行计算,若不能变为符合公式的形式,则应运用乘法法则进
行计算.
1.下列计算正确的是 ( )
A.(x+y)2=x2+y2
B.(x-y)2=x2-2xy-y2
C.(x+2y)(x-2y)=x2-2y2
D.(-x+y)2=x2-2xy+y2
检测反馈
解析:A.(x+y)2=x2+2xy+y2,故本选项错误;
B.(x-y)2=x2-2xy+y2,故本选项错误;
C.(x+2y)(x-2y)=x2- 4y2,故本选项错误;
D.(-x+y)2=(x-y)2=x2-2xy+y2,故本选项正确.故选D.
D
D
2.在下列各式中,与(a-b)2一定相等的是 ( )
A.a2+2ab+b2 B.a2-b2
C.a2+b2 D.a2-2ab+b2
解析:(a-b)2=a2-2ab+b2.故选D.
3.(x+y+z)2=( )2+2y( )+y2,两个括号内应填 ( )
A.x+y B.y+z
C.x+z D.x+y+z
解析:(x+y+z)2=(x+z)2+2y(x+z)
+y2.故选C.
C
4.计算.
(1)(a+6)2;
(2)(b-5)2;
(3)(-2a+5)2;
(4)(ab+1)(ab-1);
(5)(2a-3b)(3b+2a);
(6)(-2b-5)(2b-5);
(7)(2a+5b)2;
(8)(4a-3b)2;
(9)(-2a-1)2.
解析: (1)(7)(9)根据和的完全平方公式可得答案;(2)(3)(8)根据差的平方等于平方和减积的二倍可得答案;(4)(5)(6)根据平方差公式可得答案.
解: (1)原式=a2+12a+36.
(2)原式=b2-10b+25.
(3)原式=4a2-20a+25.
(4)原式=(ab)2-1=a2b2-1.
(5)原式=(2a)2-(3b)2=4a2-9b2.
(6)原式=(-5)2-(2b)2=25-4b2.
(7)原式=(2a)2+2×2a×5b+(5b)2
=4a2+20ab+25b2.
(8)原式=(4a)2-2×(4a)×(3b)+(3b)2
=16a2-24ab+9b2.
(9)原式=(2a)2+2×(2a)×1+12
=4a2+4a+1.
14.2.2 完全平方公式
第十四章 整式的乘法与因式分解
问题
高菲同学做作业时,把一滴墨水滴在一道数学题上,题目变成了x2■ x+1,看不清x前面的数字是什么,只知道这个二次三项式能写成一个整式的平方,急得她抓耳挠腮,你能帮助她吗?
学 习 新 知
计算(x+a)(x+b).
一、公式的推导
小活动
解:(x+a)(x+b)
=x2+bx+ax+ab
=x2+(a+b)x+ab
思考
1.在(x+a)(x+b)中,若a=b,那么上述式子将会成为怎样的式子?计算结果是什么?
变为(x+a)(x+a),计算结果是
x 2+2ax+a2,即(a+b)2=a2+2ab+b2.
思考
2.这个公式的左边和右边各有什么特点?
3.(a+b)2 =a 2 +b 2对吗?为什么?
两数和的平方,结果应该是三项式.
思考
4.你会用(a+b)2 =a 2 +2ab+b 2
计算(a-b)2吗?
将“-b”看作一个数,将(a-b)2化为[a+(-b)]2=a2+2a×(-b)+(-b)2
=a2-2ab+b2.
(a-b)2=a2 -2ab+b2
乘法公式
5.你能用图形验证:(a+b)2 =a 2 +2ab+b 2,
(a-b)2=a 2 -2ab+b 2吗?
在左图中,大正方形的面积是(a+b)2,它由两个小正方形和两个相同的长方形组成,两个小正方形的面积分别是a 2,b 2,长方形的面积是ab.所以有等式(a+b)2 =a 2 +2ab+b 2.
a+b
a+b
a
b
a
b
a-b
a-b
a
a
b
b
a+b
a+b
a
b
a
b
=
(a+b) 2
=
a2
+
2ab
+
+
b2
+
a-b
a-b
a
a
b
b
=
(a-b) 2
=
a2
-
2ab
-
+
b2
+
思考
6.比较(a+b)2=a 2+2ab+b 2及(a-b)2
=a 2 -2ab+b 2这两个公式.它们有什么不同?有什么联系?
(a+b)2 =a 2 +2ab+b 2
两数和的平方,等于它们的平方和加上这两数积的2倍.
(1)运用完全平方公式的关
键在于明确公式的特征:公式的
左边是两数和(或差)的平方,公
式的右边是一个三项式,是左
边两数的平方和加上(或减去)
左边两数积的2倍.
注意!
(2)①公式中字母的含义:公式中
字母a和b可以是具体的数,也可以
是整式(单项式或多项式).②利用
完全平方公式计算多项式的乘法,
最容易漏写2ab项,实际运算中要
特别注意.③完全平方公式与平方
差公式联合使用,要严格分清公式
的各自特点,以防混淆.
(3)逆用完全平方公式为:
a2 +2ab+b2=(a+b)2 ,
a2-2ab+b2=(a-b)2,把三项式
写成了积的形式,这是后面要
学习的因式分解.
例1 运用完全平方公式计算.
(1)(4m+n)2;
解:(1)(4m+n)2=(4m)2+2·(4m)·n+n2
=16m2 +8mn+n2.
例2 运用完全平方公式计算.
(1)1022 ; (2)992 .
解答
(2)992=(100-1)2
=1002 -2×100×1+12
=10000-200+1=9801.
(1)1022=(100+2)2
=1002 +2×100×2+22
=10000+400+4=10404.
党员两学一做自查自纠报告范文
“两学一做”自查报告
“两学一做”自查报告
红崖子沟心学校党支部
(20XX年3月28日)
根据互助县教育局《关于在教育系统党员开展“学党章党规、学系列讲话,做合格党员”学习教育活动的通知》互教委[2016]16号文件精神,我校结合实际,积极开展“两学一做”专题教育活动,并从以下几个方面进行了自查,现将我校自查报告结果简要汇报如下,不妥之处,敬请指正。
一、党员教师如何以习近平系列讲话指导教育教学工作 深入学习贯彻讲话精神,是在思想上政治上行动上同以习近平同志为总书记的党央保持高度一致的迫切需要。学习好、贯彻好讲话精神,对于促进党员教师进一步凝聚发展共识、明确改革方向,增强教育改革的活力和发展的动力,推进教育事业科学发展,努力办好人民满意的教育,具有十分重要的意义。为此,在专题学习讨论会上,我校党支部书记靳永录就面向全体学生,如何促进学生全面发展和主动发展
是素质教育的核心理念这一问题做了严格要求。首先,从全面贯彻党的教育方针,全面提高教育教学质量入手,进一步明确教师职责,扎实开展教学工作。其次,学校通过讲座、学习讨论等形式转变教师的思想认识,提高教师实
讨论
现有下图所示三种规格的卡片各若干张,请你根据二次三项式a2 +2ab+b2,选取相应种类和数量的卡片,尝试拼成一个正方形,并讨论该正方形的代数意义.
思考、讨论
(a+b)2与(-a-b)2相等吗?(a-b)2与(b-a)2相等吗?(a-b)2与a 2-b 2相等吗?为什么?
运用乘法公式计算,有时要在式子中添括号,在第二章中,我们学过去括号法则,即a+(b+c)=a+b+c;a-(b+c)=a-b-c.
反过来,就得到添括号法则:a+b+c=a+(b+c);a-b-c=a-(b+c).
添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号.
说明
(1)添括号法则与去括号法则是一致的,添括号正确与否,可用去括号进行检验.
(2)添括号时,如果括号前面是负号,那么括到括号里的各项都改变符号,不能只改变部分项的符号.
知识拓展
解:(1)(x+2y-3)(x-2y+3)=[x+(2y-3)][x-(2y-3)]
=x2 -(2y-3)2=x2-(4y2 -12y+9)=x2-4y2+12y-9.
(2)(a+b+c)2=[(a+b)+c]2=(a+b)2+2(a+b)c+c2
=a2 +2ab+b2 +2ac+2bc+c2
=a2 +b2 +c2 +2ab+2ac+2bc.
例题示范
例3.运用乘法公式计算.
(x+2y-3)(x-2y+3);
(a+b+c)2.
一些本来不是二项式的式子的平方也可以利用完全平方公式来计算,关键是使其转化为二项式的平方,如计算(a+b+c)2,可以把这个代数式转化为[a+(b+c)]2或[(a+b)+c]2,把b+c或a+b看做是一个整体(一个字母),也可以把这个式子转化为[(a+c)+b]2.实际操作时要看怎样做最有利于计算.
完全平方公式是进行整式乘法的重要工具,它的结构形式具有对称性,两个公式都叫做完全平方公式,前面的一个叫做和的完全平方公式,后面的一个叫做差的完全平方公式.判断一个式子能不能用完全平方公式展开,主要看它的结构形式是否符合公式要求,习惯上把(a±b)2 中的a叫做前项,b叫做后项,记忆时巧记为“首平方,末平方,首末两倍中间放”.
知识小结
2.添括号
添括号时,如果括号前面是正号,
括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号.
应用时,主要关注两点:一是关注括号前面的符号是正号还是负号;二是对
照添括号前和后符号该不该改变.
3.运用完全平方公式还应注意以下几点:
①切勿把完全平方公式与公式(ab)2 =a2b2相混淆,或随意写成(a+b)2 =a2 +b2;
②切勿把“乘积项”2ab中的2丢掉;
③计算时,要先观察题目特点,看是否符合公式的条件,若不符合,应先变形为符合公式的形式,再利用公式进行计算,若不能变为符合公式的形式,则应运用乘法法则进
行计算.
1.下列计算正确的是 ( )
A.(x+y)2=x2+y2
B.(x-y)2=x2-2xy-y2
C.(x+2y)(x-2y)=x2-2y2
D.(-x+y)2=x2-2xy+y2
检测反馈
解析:A.(x+y)2=x2+2xy+y2,故本选项错误;
B.(x-y)2=x2-2xy+y2,故本选项错误;
C.(x+2y)(x-2y)=x2- 4y2,故本选项错误;
D.(-x+y)2=(x-y)2=x2-2xy+y2,故本选项正确.故选D.
D
D
2.在下列各式中,与(a-b)2一定相等的是 ( )
A.a2+2ab+b2 B.a2-b2
C.a2+b2 D.a2-2ab+b2
解析:(a-b)2=a2-2ab+b2.故选D.
3.(x+y+z)2=( )2+2y( )+y2,两个括号内应填 ( )
A.x+y B.y+z
C.x+z D.x+y+z
解析:(x+y+z)2=(x+z)2+2y(x+z)
+y2.故选C.
C
4.计算.
(1)(a+6)2;
(2)(b-5)2;
(3)(-2a+5)2;
(4)(ab+1)(ab-1);
(5)(2a-3b)(3b+2a);
(6)(-2b-5)(2b-5);
(7)(2a+5b)2;
(8)(4a-3b)2;
(9)(-2a-1)2.
解析: (1)(7)(9)根据和的完全平方公式可得答案;(2)(3)(8)根据差的平方等于平方和减积的二倍可得答案;(4)(5)(6)根据平方差公式可得答案.
解: (1)原式=a2+12a+36.
(2)原式=b2-10b+25.
(3)原式=4a2-20a+25.
(4)原式=(ab)2-1=a2b2-1.
(5)原式=(2a)2-(3b)2=4a2-9b2.
(6)原式=(-5)2-(2b)2=25-4b2.
(7)原式=(2a)2+2×2a×5b+(5b)2
=4a2+20ab+25b2.
(8)原式=(4a)2-2×(4a)×(3b)+(3b)2
=16a2-24ab+9b2.
(9)原式=(2a)2+2×(2a)×1+12
=4a2+4a+1.
