人教版七年级数学下册5.3.1 平行线的性质 教学课件(共41张PPT)
文档属性
| 名称 | 人教版七年级数学下册5.3.1 平行线的性质 教学课件(共41张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 796.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-17 22:24:29 | ||
图片预览







文档简介
(共41张PPT)
5.3 平行线的性质
5.3.1 平行线的性质
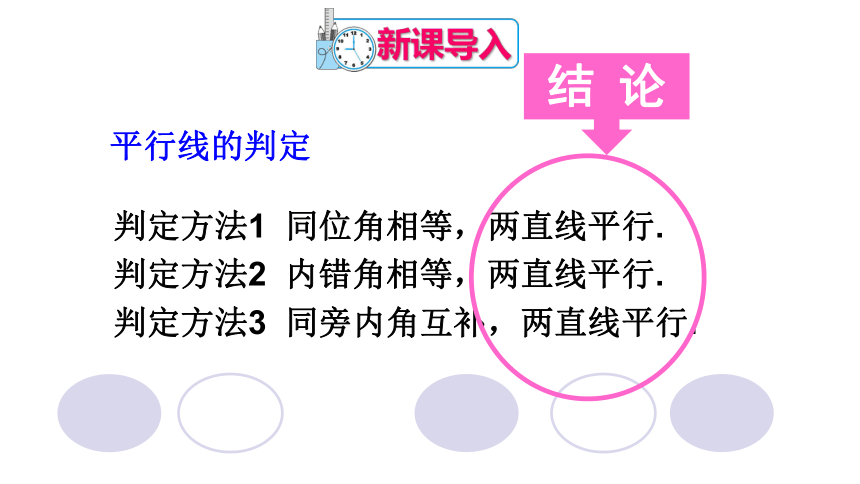
判定方法1 同位角相等,两直线平行.
判定方法2 内错角相等,两直线平行.
判定方法3 同旁内角互补,两直线平行.
结 论
平行线的判定
新课导入
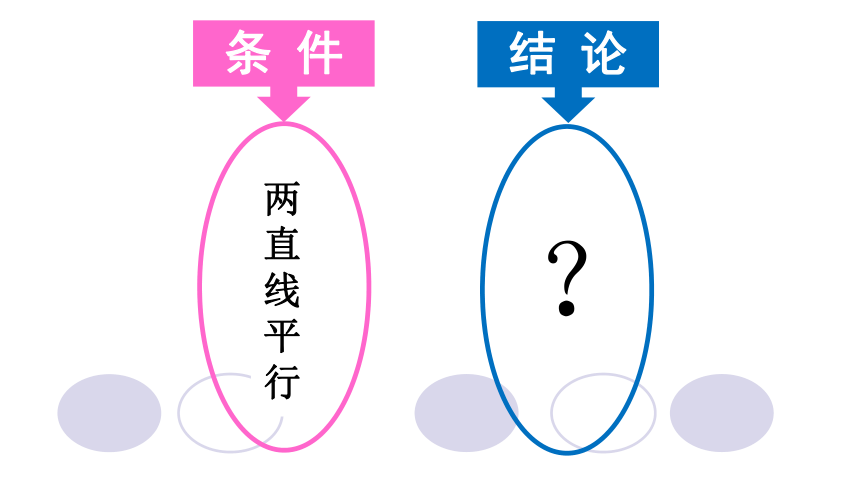
两
直
线
平
行
条 件
结 论
?
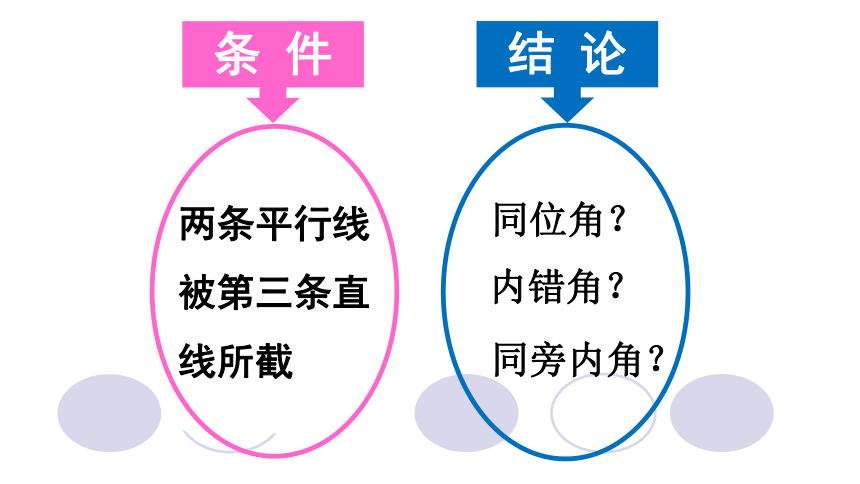
两条平行线
被第三条直
线所截
同位角?
内错角?
同旁内角?
条 件
结 论
学习目标:
1.能叙述平行线的三条性质.
2.能运用平行线的三条性质进行简单的推理和计算.
学习重、难点:
重点:对平行线性质的理解及它们与平行线的判定之间的关系.
难点:性质2和性质3的推理过程的逻辑表述.
探究新知
知识点1
平行线
思考
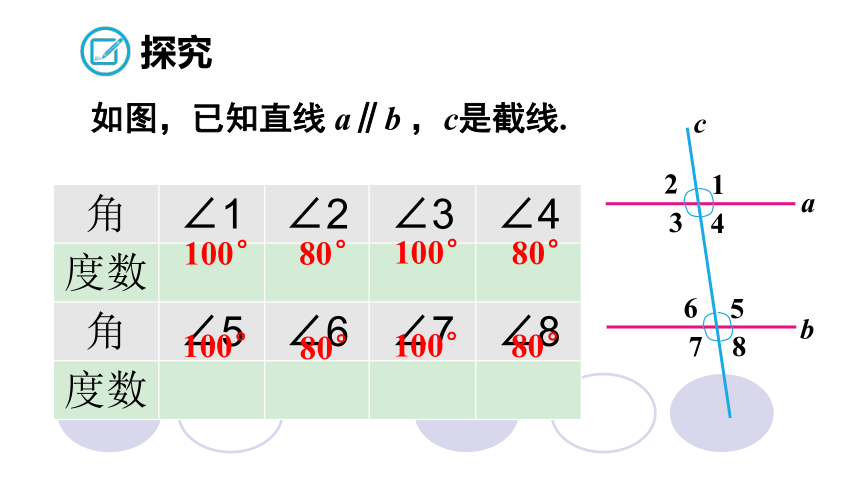
两条平行线被第三条直线截得的同位角会具有怎样的数量关系?
如图,已知直线 a∥b ,c是截线.
b
a
c
1
2
3
4
5
6
7
8
探究
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
100°
80°
100°
80°
100°
80°
100°
80°
∠1,∠2,···,∠8中,哪些是同位角?它们的度数具有什么关系?
由此猜想:
两条平行线被第三条直线截得的同位角具有什么关系?
相等
b
a
c
1
2
3
4
5
6
7
8
再任意画一条截线 d,同样度量并比较各对同位角的度数,你的猜想还成立吗?
b
a
c
1
2
3
4
5
6
7
8
d
成立
性质1 两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
归纳
上一节,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”. 类似地,你能由性质 1 推出两条平行线被第三条直线所截,内错角之间的关系吗?
思考
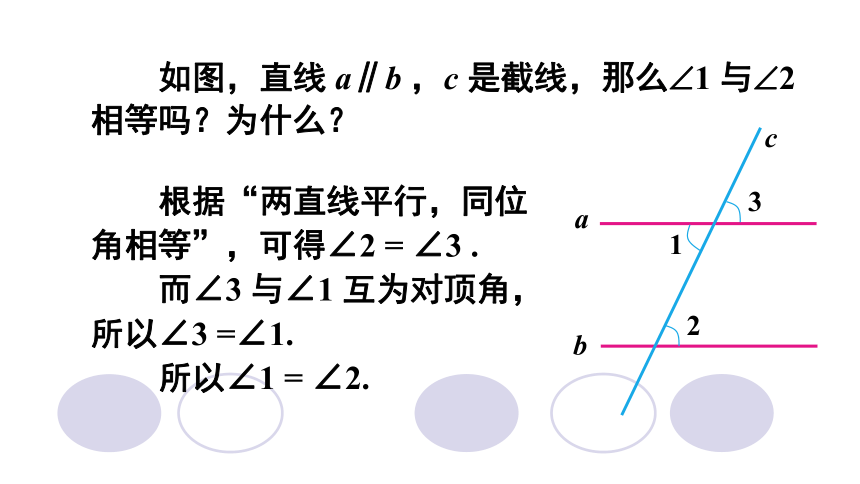
如图,直线 a∥b ,c 是截线,那么?1 与?2 相等吗?为什么?
根据“两直线平行,同位角相等”,可得∠2 = ∠3 .
而∠3 与∠1 互为对顶角,所以∠3 =∠1.
所以∠1 = ∠2.
b
a
c
3
2
1
性质2 两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
归纳
性质3 两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
类似地,
例1 如图,是一块梯形铁片的残余部分,量得∠A = 100 ° ,∠B = 115 ° ,梯形的另外两个角分别是多少度?
解:因为梯形上、下两底 AB∥CD ,根据“两直线平行,同旁内角互补”,可得∠A与∠D 互补,∠B与∠C 互补.
于是∠D = 180 ° -∠A
= 180 ° -100? = 80 ° ,
∠C = 180 ° -∠B
= 180 ° -115 ° = 65 ° .
所以,梯形的另外两个角分别是80 ° ,65°.
答:∠2 = 110 ° .因为AB∥CD,∠1 和 ∠2 是内错角,根据两直线平行,内错角相等,得到∠1 = ∠2.因为∠1 = 110 ° ,所以∠2 = 110 ° .
例2 如图,平行线 AB ,CD 被直线 AE 所截.
(1)从∠1 = 110 ° .可以知道∠2是多少度吗?为什么?
例2 如图,平行线 AB ,CD 被直线 AE 所截.
(2)从∠1 = 110 ° .可以知道∠3是多少度吗?为什么?
答:∠3 = 110 ° .因为AB∥CD ,∠1和∠3是同位角,根据两直线平行,同位角相等,得到∠1 = ∠3.因为∠1 = 110 ° ,所以∠3 = 110 ° .
例2 如图,平行线 AB ,CD 被直线 AE 所截.
(3)从∠1 = 110 ° .可以知道∠4是多少度吗?为什么?
答:∠4 = 70 ° .因为AB∥CD , ∠1和∠4是同旁内角,根据两直线平行,同旁内角互补,得到∠1 +∠4 = 180 ° .因为∠1 = 110 ° ,所以∠4 = 70 ° .
例3 如图,已知 AB∥CD,AE∥CF,∠A = 39°,∠C 是多少度?为什么?
方法一
解:∵AB∥CD,
∴ ∠C =∠1.
∵ AE∥CF,
∴ ∠A =∠1.
∴ ∠C =∠A.
∵∠A = 39 ° ,
∴∠C = 39 ° .
1
2
方法二
解:∵AB∥CD,∴ ∠C =∠2.
∵ AE∥CF,
∴ ∠A =∠2.
∴ ∠C =∠A.
∵∠A = 39 ° ,
∴∠C = 39 ° .
对比平行线的性质和判定方法,你能说出它们的区别吗?
条件 结论
判定 同位角相等 两直线平行
内错角相等
同旁内角互补
性质 两直线平行 同位角相等
内错角相等
同旁内角互补
练习
1. 如图,直线 a∥b,∠1 = 54°,∠2,∠3,∠4各是多少度?
解:∵a∥b,∠1=54°,∴∠4 =∠1 = 54°(两直线平行,同位角相等).
∠3 =180°-∠4
=180° - 54°=126°,
∠2与∠1是对顶角,∴∠2=∠1= 54°.
2. 如图,在△ABC 中,D 是 AB 上一点,E 是 AC 上一点, ∠ADE = 60°,∠B = 60°,∠AED = 40°.
(1)DE 与 BC 平行吗?为什么?
(2)∠C 是多少度?为什么?
解:(1)∵∠ADE = ∠B,∴DE∥BC(同位角相等,两直线平行)
(2)∵DE∥BC,∴∠C = ∠AED = 40°(两直线平行,同位角相等)
1. 如图,已知直线 a,b 被直线 c 所截,以下结论正确的有( )
①∠1 =∠2;②∠1 =∠3;
③∠2 =∠3;④∠3+∠4 = 180°.
A.1个 B.2个 C.3个 D.4个
误区一 利用平行线的性质时易忽视两直线平行的前提条件
错 解
正 解
D
A
错因分析
由于题中未说明 a∥b ,故只能根据对顶角相等得①成立. 在没有给定两条直线平行的条件时,同位角、内错角、同旁内角的数量关系是不确定的.
2. 如图所示,AB∥CD,∠1=∠2. 试说明:BE∥PF .
误区二 不能正确利用平行线的性质解题
错 解
因为AB∥CD,所以∠ABP =∠BPD,又因为∠1 =∠3,∠2 =∠4,∠1 =∠2,所以∠3 = ∠4 .所以 BE∥PF .
因为AB∥CD(已知),
所以∠APB = ∠BPD(两直线平行,内错角相等),
因为∠1 = ∠2,
所以∠ABP -∠1 = ∠BPD-∠2(等式性质),
即∠3 = ∠4,
所以 BE∥PF(内错角相等,两直线平行).
正 解
错因分析
错解中由 AB∥CD 推出∠ABP = ∠BPD 这一步是盲目的,因为后面的证明没有用上这一结论,另外题目中并没有指明 BE,PF 分别是∠ABP , ∠BPD 的平分线,而错解中却想当然地把它作为“需要”的已知条件来使用,说理时应注意仔细分析题设条件.
基础巩固
随堂演练
1. 如图,由AB∥CD可以得到( )
A.∠1=∠2 B.∠2=∠3
C.∠1=∠4 D.∠3=∠4
C
2. 如图,如果 AB∥CD∥EF ,那么∠BAC + ∠ACE + ∠CEF =( )
A.180° B.270° C.360° D.540°
C
3. 如图,要在公路的两侧铺设平行管道,如果公路一侧铺设的管道与纵向联通管道的角度为120°,那么,为了使管道对接,另一侧应以____角度铺设纵向联通管道,根据是______________
_______________ .
两直线平行,同旁内角互补
60°
?
120°
4. 光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,∠1=45°,∠2=122°,求图中其他角的度数.
综合运用
解:由题意得:
∠3 =∠1 = 45°,∠1+∠7 = 180°,∴∠7 = 180°-∠1 = 135°.
∴∠8 =∠7 = 135°.
又∠4 =∠2 = 122°,∠2 +∠5 = 180°,∴∠5 = 180°-∠2 = 58°.
∴∠6=∠5=58°.
图形 已知 结果 理由
a∥b ∠1=∠3
∠2=∠4
a∥b 两直线平行,同旁内角互补
两直线平行,同位角相等
a∥b
两直线平行,内错角相等
∠2+∠3=180°
b
a
c
1
2
3
4
课堂小结
拓展延伸
如图,直线 DE 经过点 A,DE∥BC,∠B=44°,∠C=57°.
(1)∠DAB 等于多少度?为什么?
(2)∠EAC 等于多少度?为什么?
(3)∠BAC 等于多少度?
(4)由(1)、(2)、(3)
的结果,你能说明为什么三角形
的内角和是180°吗?
解:(1)∠DAB = 44°.
∵DE∥BC,
∴∠DAB =∠B = 44°
(两直线平行,内错角相等).
(2)∠EAC = 57°.
∵DE∥BC,∴∠EAC =∠C = 57°(两直线平行,内错角相等).
(3)∠BAC = 180°-∠DAB -∠EAC = 180°- 44°- 57°= 79°.
1. 从课后习题中选取;
2. 完成练习册本课时的习题。
课后作业
教学反思
这节课比较成功的地方是:①对教学的方式进行了一定的尝试,注重学生的分析能力,启发学生用不同方法解决问题.②尽量锻炼学生使用规范性的几何语言.不足的是师生之间的互动配合和默契程度有待加强.
5.3 平行线的性质
5.3.1 平行线的性质
判定方法1 同位角相等,两直线平行.
判定方法2 内错角相等,两直线平行.
判定方法3 同旁内角互补,两直线平行.
结 论
平行线的判定
新课导入
两
直
线
平
行
条 件
结 论
?
两条平行线
被第三条直
线所截
同位角?
内错角?
同旁内角?
条 件
结 论
学习目标:
1.能叙述平行线的三条性质.
2.能运用平行线的三条性质进行简单的推理和计算.
学习重、难点:
重点:对平行线性质的理解及它们与平行线的判定之间的关系.
难点:性质2和性质3的推理过程的逻辑表述.
探究新知
知识点1
平行线
思考
两条平行线被第三条直线截得的同位角会具有怎样的数量关系?
如图,已知直线 a∥b ,c是截线.
b
a
c
1
2
3
4
5
6
7
8
探究
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
100°
80°
100°
80°
100°
80°
100°
80°
∠1,∠2,···,∠8中,哪些是同位角?它们的度数具有什么关系?
由此猜想:
两条平行线被第三条直线截得的同位角具有什么关系?
相等
b
a
c
1
2
3
4
5
6
7
8
再任意画一条截线 d,同样度量并比较各对同位角的度数,你的猜想还成立吗?
b
a
c
1
2
3
4
5
6
7
8
d
成立
性质1 两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
归纳
上一节,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”. 类似地,你能由性质 1 推出两条平行线被第三条直线所截,内错角之间的关系吗?
思考
如图,直线 a∥b ,c 是截线,那么?1 与?2 相等吗?为什么?
根据“两直线平行,同位角相等”,可得∠2 = ∠3 .
而∠3 与∠1 互为对顶角,所以∠3 =∠1.
所以∠1 = ∠2.
b
a
c
3
2
1
性质2 两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
归纳
性质3 两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
类似地,
例1 如图,是一块梯形铁片的残余部分,量得∠A = 100 ° ,∠B = 115 ° ,梯形的另外两个角分别是多少度?
解:因为梯形上、下两底 AB∥CD ,根据“两直线平行,同旁内角互补”,可得∠A与∠D 互补,∠B与∠C 互补.
于是∠D = 180 ° -∠A
= 180 ° -100? = 80 ° ,
∠C = 180 ° -∠B
= 180 ° -115 ° = 65 ° .
所以,梯形的另外两个角分别是80 ° ,65°.
答:∠2 = 110 ° .因为AB∥CD,∠1 和 ∠2 是内错角,根据两直线平行,内错角相等,得到∠1 = ∠2.因为∠1 = 110 ° ,所以∠2 = 110 ° .
例2 如图,平行线 AB ,CD 被直线 AE 所截.
(1)从∠1 = 110 ° .可以知道∠2是多少度吗?为什么?
例2 如图,平行线 AB ,CD 被直线 AE 所截.
(2)从∠1 = 110 ° .可以知道∠3是多少度吗?为什么?
答:∠3 = 110 ° .因为AB∥CD ,∠1和∠3是同位角,根据两直线平行,同位角相等,得到∠1 = ∠3.因为∠1 = 110 ° ,所以∠3 = 110 ° .
例2 如图,平行线 AB ,CD 被直线 AE 所截.
(3)从∠1 = 110 ° .可以知道∠4是多少度吗?为什么?
答:∠4 = 70 ° .因为AB∥CD , ∠1和∠4是同旁内角,根据两直线平行,同旁内角互补,得到∠1 +∠4 = 180 ° .因为∠1 = 110 ° ,所以∠4 = 70 ° .
例3 如图,已知 AB∥CD,AE∥CF,∠A = 39°,∠C 是多少度?为什么?
方法一
解:∵AB∥CD,
∴ ∠C =∠1.
∵ AE∥CF,
∴ ∠A =∠1.
∴ ∠C =∠A.
∵∠A = 39 ° ,
∴∠C = 39 ° .
1
2
方法二
解:∵AB∥CD,∴ ∠C =∠2.
∵ AE∥CF,
∴ ∠A =∠2.
∴ ∠C =∠A.
∵∠A = 39 ° ,
∴∠C = 39 ° .
对比平行线的性质和判定方法,你能说出它们的区别吗?
条件 结论
判定 同位角相等 两直线平行
内错角相等
同旁内角互补
性质 两直线平行 同位角相等
内错角相等
同旁内角互补
练习
1. 如图,直线 a∥b,∠1 = 54°,∠2,∠3,∠4各是多少度?
解:∵a∥b,∠1=54°,∴∠4 =∠1 = 54°(两直线平行,同位角相等).
∠3 =180°-∠4
=180° - 54°=126°,
∠2与∠1是对顶角,∴∠2=∠1= 54°.
2. 如图,在△ABC 中,D 是 AB 上一点,E 是 AC 上一点, ∠ADE = 60°,∠B = 60°,∠AED = 40°.
(1)DE 与 BC 平行吗?为什么?
(2)∠C 是多少度?为什么?
解:(1)∵∠ADE = ∠B,∴DE∥BC(同位角相等,两直线平行)
(2)∵DE∥BC,∴∠C = ∠AED = 40°(两直线平行,同位角相等)
1. 如图,已知直线 a,b 被直线 c 所截,以下结论正确的有( )
①∠1 =∠2;②∠1 =∠3;
③∠2 =∠3;④∠3+∠4 = 180°.
A.1个 B.2个 C.3个 D.4个
误区一 利用平行线的性质时易忽视两直线平行的前提条件
错 解
正 解
D
A
错因分析
由于题中未说明 a∥b ,故只能根据对顶角相等得①成立. 在没有给定两条直线平行的条件时,同位角、内错角、同旁内角的数量关系是不确定的.
2. 如图所示,AB∥CD,∠1=∠2. 试说明:BE∥PF .
误区二 不能正确利用平行线的性质解题
错 解
因为AB∥CD,所以∠ABP =∠BPD,又因为∠1 =∠3,∠2 =∠4,∠1 =∠2,所以∠3 = ∠4 .所以 BE∥PF .
因为AB∥CD(已知),
所以∠APB = ∠BPD(两直线平行,内错角相等),
因为∠1 = ∠2,
所以∠ABP -∠1 = ∠BPD-∠2(等式性质),
即∠3 = ∠4,
所以 BE∥PF(内错角相等,两直线平行).
正 解
错因分析
错解中由 AB∥CD 推出∠ABP = ∠BPD 这一步是盲目的,因为后面的证明没有用上这一结论,另外题目中并没有指明 BE,PF 分别是∠ABP , ∠BPD 的平分线,而错解中却想当然地把它作为“需要”的已知条件来使用,说理时应注意仔细分析题设条件.
基础巩固
随堂演练
1. 如图,由AB∥CD可以得到( )
A.∠1=∠2 B.∠2=∠3
C.∠1=∠4 D.∠3=∠4
C
2. 如图,如果 AB∥CD∥EF ,那么∠BAC + ∠ACE + ∠CEF =( )
A.180° B.270° C.360° D.540°
C
3. 如图,要在公路的两侧铺设平行管道,如果公路一侧铺设的管道与纵向联通管道的角度为120°,那么,为了使管道对接,另一侧应以____角度铺设纵向联通管道,根据是______________
_______________ .
两直线平行,同旁内角互补
60°
?
120°
4. 光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,∠1=45°,∠2=122°,求图中其他角的度数.
综合运用
解:由题意得:
∠3 =∠1 = 45°,∠1+∠7 = 180°,∴∠7 = 180°-∠1 = 135°.
∴∠8 =∠7 = 135°.
又∠4 =∠2 = 122°,∠2 +∠5 = 180°,∴∠5 = 180°-∠2 = 58°.
∴∠6=∠5=58°.
图形 已知 结果 理由
a∥b ∠1=∠3
∠2=∠4
a∥b 两直线平行,同旁内角互补
两直线平行,同位角相等
a∥b
两直线平行,内错角相等
∠2+∠3=180°
b
a
c
1
2
3
4
课堂小结
拓展延伸
如图,直线 DE 经过点 A,DE∥BC,∠B=44°,∠C=57°.
(1)∠DAB 等于多少度?为什么?
(2)∠EAC 等于多少度?为什么?
(3)∠BAC 等于多少度?
(4)由(1)、(2)、(3)
的结果,你能说明为什么三角形
的内角和是180°吗?
解:(1)∠DAB = 44°.
∵DE∥BC,
∴∠DAB =∠B = 44°
(两直线平行,内错角相等).
(2)∠EAC = 57°.
∵DE∥BC,∴∠EAC =∠C = 57°(两直线平行,内错角相等).
(3)∠BAC = 180°-∠DAB -∠EAC = 180°- 44°- 57°= 79°.
1. 从课后习题中选取;
2. 完成练习册本课时的习题。
课后作业
教学反思
这节课比较成功的地方是:①对教学的方式进行了一定的尝试,注重学生的分析能力,启发学生用不同方法解决问题.②尽量锻炼学生使用规范性的几何语言.不足的是师生之间的互动配合和默契程度有待加强.
