苏教版四年级下册数学课件--6 运算律 第6课时 运用运算定律解决实际问题(13张PPT)
文档属性
| 名称 | 苏教版四年级下册数学课件--6 运算律 第6课时 运用运算定律解决实际问题(13张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 15:19:05 | ||
图片预览




文档简介
(共13张PPT)
数学四年级
下册
第六单元
运算律
第6课时
运用运算定律解决实际问题
一、回顾旧知导入新课
回答下面各题并说出数量关系。
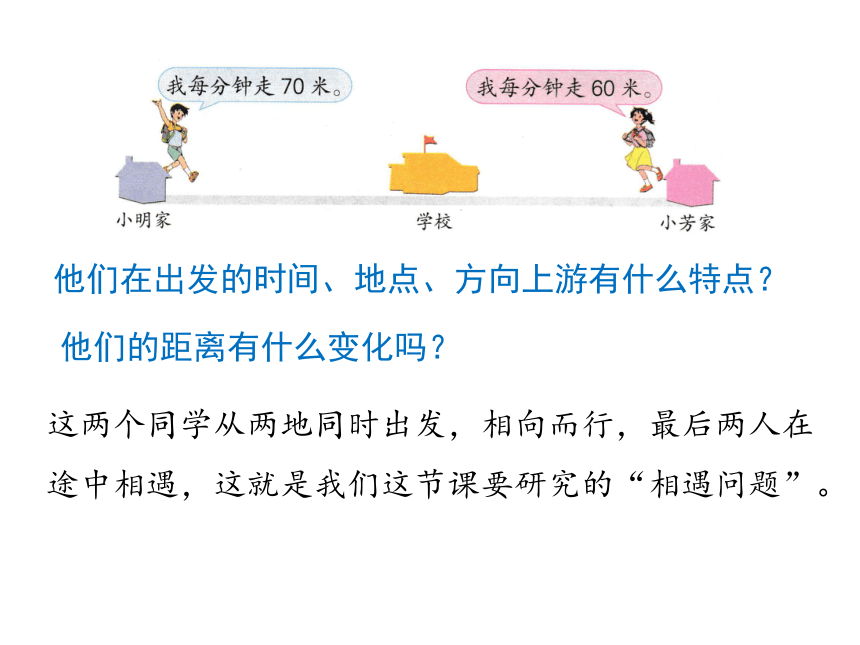
(1)小明每分钟走70米,走了4分钟,一共走了多少米?
(2)小芳每分钟走60米,走了4分钟,一共走了多少米?
速度×时间=路程
他们在出发的时间、地点、方向上游有什么特点?
他们的距离有什么变化吗?
这两个同学从两地同时出发,相向而行,最后两人在途中相遇,这就是我们这节课要研究的“相遇问题”。
二、创设情境探究新知
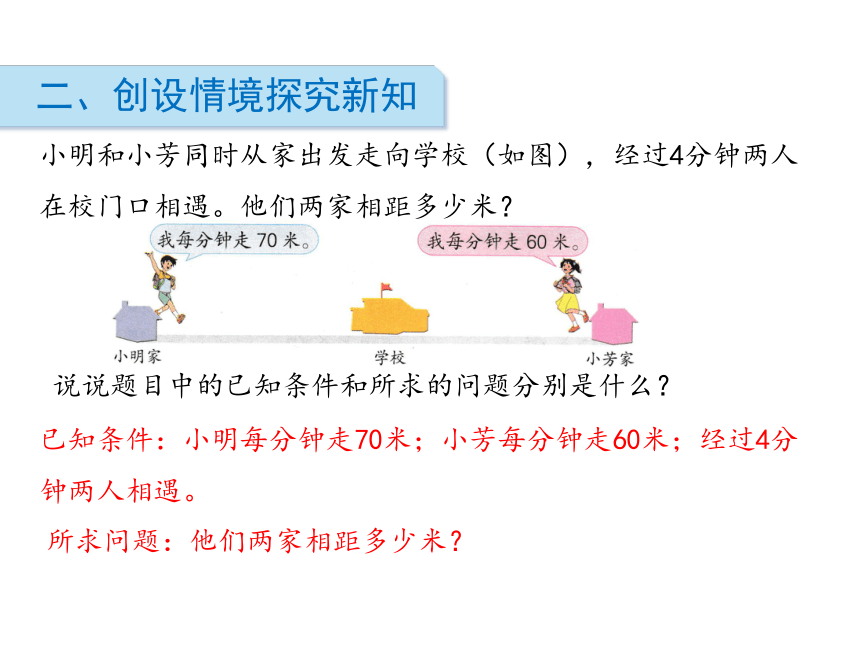
小明和小芳同时从家出发走向学校(如图),经过4分钟两人在校门口相遇。他们两家相距多少米?
说说题目中的已知条件和所求的问题分别是什么?
已知条件:小明每分钟走70米;小芳每分钟走60米;经过4分钟两人相遇。
所求问题:他们两家相距多少米?
我们找到了这么多信息,想一想,我们学过了哪些解决问题的策略呢?
列表、画图。
你打算用什么策略把这些信息整理出来?
画图整理:
列表整理:
你能根据整理的结果,分析数量关系确定先算什么吗?
思路一:小明走的路程加上小芳走的路程就是他们两家相距的路程,可以先分别算出小明和小芳走的路程,再把两个人走的路程相加,就是他们两家相距的路程。
思路二:两人4分钟一共走的路程,就是两家相距的路程,可以先算两人的速度和,再把“速度和×相遇时间”就等于总路程。
根据不同的解题思路,用两种不同的方法进行解答。
解法一:
70×7+60×4
=280+240
=520(米)
解法二:
(70+60)×4
=130×4
=520(米)
这两种方法的得数相同,可以用什么符号将它们连起来?
观察等式,你想到了那个运算律?
乘法分配律
回顾解决问题的过程,你有什么体会?
画图和列表都可以帮助我们理解题意;线段图可以帮助我们找到不同的解题方法;要注意寻找不同解法之间的联系。
张小华和赵丽同时从同一地点出发,张小华向东走,速度是60米/分;赵丽向西走,速度是55米/分。经过3分钟,两人相距多少米?(先画图整理,再解答)
3分钟
3分钟
赵丽68米/分
张小华60米/分
60×3+55×3
=180+165
=345(米)
答:两人相距345米。
三、巩固练习
王超和李明同时从两地沿一条公路面对面走来。王超的速度是68米/分,经过6分钟两人相遇。两地间的路程是多少米?(先画图整理,再解答)
6分钟相遇
王超68米/分
李明65米/分
?米
(68+65)×6
=133×6
=798(米)
答:两地间的路程是798米。
两个工程队合开一条隧道,分别从隧道的一端同时向中间开凿12米,第二队每天开凿15米,经过8天正好凿通。这条隧道长多少米?
(12+15)×8
=27×8
=216(米)
答:这条隧道长216米。
四、课堂小结
计算“相遇问题”中的总路程时,可以先分别计算出每个人行的路程,再求总路程;也可以求出两个人的速度和,再用“速度和×相遇时间”来计算总路程。
数学四年级
下册
第六单元
运算律
第6课时
运用运算定律解决实际问题
一、回顾旧知导入新课
回答下面各题并说出数量关系。
(1)小明每分钟走70米,走了4分钟,一共走了多少米?
(2)小芳每分钟走60米,走了4分钟,一共走了多少米?
速度×时间=路程
他们在出发的时间、地点、方向上游有什么特点?
他们的距离有什么变化吗?
这两个同学从两地同时出发,相向而行,最后两人在途中相遇,这就是我们这节课要研究的“相遇问题”。
二、创设情境探究新知
小明和小芳同时从家出发走向学校(如图),经过4分钟两人在校门口相遇。他们两家相距多少米?
说说题目中的已知条件和所求的问题分别是什么?
已知条件:小明每分钟走70米;小芳每分钟走60米;经过4分钟两人相遇。
所求问题:他们两家相距多少米?
我们找到了这么多信息,想一想,我们学过了哪些解决问题的策略呢?
列表、画图。
你打算用什么策略把这些信息整理出来?
画图整理:
列表整理:
你能根据整理的结果,分析数量关系确定先算什么吗?
思路一:小明走的路程加上小芳走的路程就是他们两家相距的路程,可以先分别算出小明和小芳走的路程,再把两个人走的路程相加,就是他们两家相距的路程。
思路二:两人4分钟一共走的路程,就是两家相距的路程,可以先算两人的速度和,再把“速度和×相遇时间”就等于总路程。
根据不同的解题思路,用两种不同的方法进行解答。
解法一:
70×7+60×4
=280+240
=520(米)
解法二:
(70+60)×4
=130×4
=520(米)
这两种方法的得数相同,可以用什么符号将它们连起来?
观察等式,你想到了那个运算律?
乘法分配律
回顾解决问题的过程,你有什么体会?
画图和列表都可以帮助我们理解题意;线段图可以帮助我们找到不同的解题方法;要注意寻找不同解法之间的联系。
张小华和赵丽同时从同一地点出发,张小华向东走,速度是60米/分;赵丽向西走,速度是55米/分。经过3分钟,两人相距多少米?(先画图整理,再解答)
3分钟
3分钟
赵丽68米/分
张小华60米/分
60×3+55×3
=180+165
=345(米)
答:两人相距345米。
三、巩固练习
王超和李明同时从两地沿一条公路面对面走来。王超的速度是68米/分,经过6分钟两人相遇。两地间的路程是多少米?(先画图整理,再解答)
6分钟相遇
王超68米/分
李明65米/分
?米
(68+65)×6
=133×6
=798(米)
答:两地间的路程是798米。
两个工程队合开一条隧道,分别从隧道的一端同时向中间开凿12米,第二队每天开凿15米,经过8天正好凿通。这条隧道长多少米?
(12+15)×8
=27×8
=216(米)
答:这条隧道长216米。
四、课堂小结
计算“相遇问题”中的总路程时,可以先分别计算出每个人行的路程,再求总路程;也可以求出两个人的速度和,再用“速度和×相遇时间”来计算总路程。
