2.2.1 椭圆的标准方程 课件 22张PPT
文档属性
| 名称 | 2.2.1 椭圆的标准方程 课件 22张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 951.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-18 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
习总书记说:航天梦是强国梦的组成部分,
随着中国航天事业的快速发展,中国人探
索太空的脚步会迈的更大、更远!
2.2.1椭圆及其标准方程
圆的定义:到定点的距离等于定长的点的轨迹
温故而知新
(1)取一条细绳zxxk
(2)把它的两端固定在板上的两点F1、F2
(3)用铅笔尖(M)把细绳拉紧,在板上慢慢移动看看画出的图形
学生实验
思考:1.那些量发生了变化,那些量没有变?
2.有定点,是什么?
3.有定长吗,是什么?
4.动点满足的关系式?
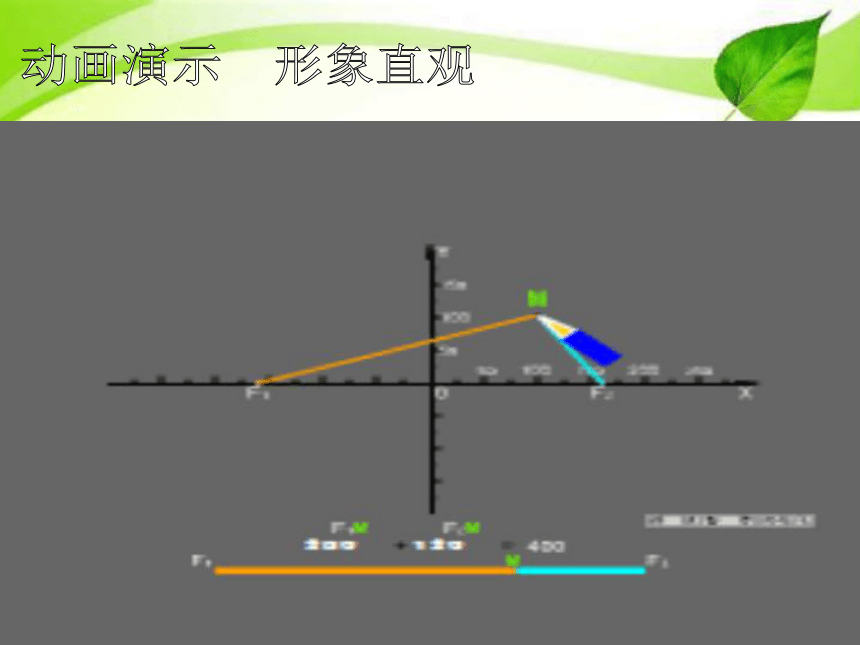
动画演示 形象直观
1、椭圆的定义:
平面内到两个定点F1、F2的距离之和等于常数
的动点M的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距。即|F1F2|
M
2、椭圆定义式:|MF1| + |MF2| = 常数(> |F1F2|)则M点的轨迹是椭圆.
(大于|F1F2|)
总结实验结论
F1
F2
M
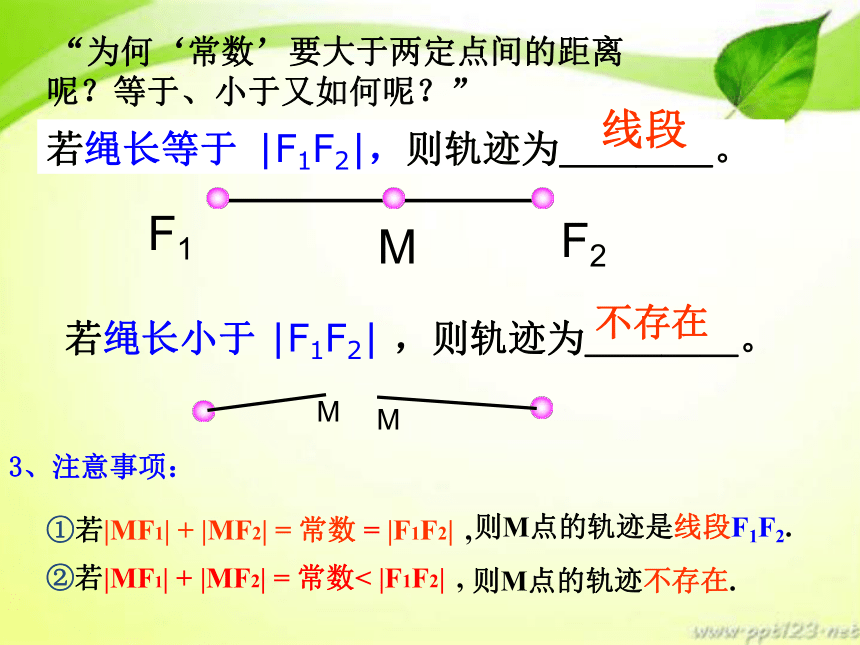
若绳长小于 |F1F2| ,则轨迹为____。
若绳长等于 |F1F2|,则轨迹为____。
线段
不存在
M
M
①若|MF1| + |MF2| = 常数 = |F1F2| ,
则M点的轨迹是线段F1F2.
②若|MF1| + |MF2| = 常数< |F1F2| ,
则M点的轨迹不存在.
3、注意事项:
“为何‘常数’要大于两定点间的距离呢?等于、小于又如何呢?”
1.两点间距离公式:
2.求曲线方程的基本步骤:
1、建系
2、设动点
3、限制条件
4、代方程
5、化简
预备知识回顾:
标准方程的推导
? 探讨建立平面直角坐标系的方案
建立平面直角坐标系通常遵循的原则:“对称”、“简洁”
O
x
y
M
F1
F2
方案一
O
x
y
方案二
F1
F2
M
F1
F2
x
y
M( x , y )
F1
F2
x
y
M( x , y )
椭圆上的点M满足|MF1|+|MF2|为定值,
设定值为2a, ︳F1F2︱=2c ,且2a>2c
即:
O
标准方程的推导
即:
则|MF1|+|MF2|=2a
观察左图, 你能从中找出表示 c 、 a 的线段吗? a2-c2 有什么几何意义?
这是焦点在 x 轴上的椭圆的标准方程。
则方程可化为
思考
?
当椭圆的焦点在y轴上时,它的标准方程是怎样 的呢?
想一想
①
②
标准方程中,分母哪个大,焦点就在哪个轴上!
标 准 方 程
相 同 点
焦点位置的判断
不 同 点
图 形
焦 点 坐 标
a、b、c 的关系
焦点在x轴上
焦点在y轴上
y
x
M
O
F1
F2
例1 (1)椭圆
中a=
____,
b=
___,
C=
___.
10
6
8
变式训练1: 若椭圆的方程为
则a= , b= ,c= .
运用新知,解决问题
椭圆标准方程中 和 对应的分母哪个大,
则焦点在哪个轴上.
解题反思
例2 已知椭圆的两个焦点坐标分别是(-2,0),
(2,0), 并且经过点 .求它的标准方程.
解:因为椭圆的焦点在x轴上,所以设
它的标准方程为
由椭圆的定义知
巩固提高
又因为 ,所以
因此, 所求椭圆的标准方程为
所以
能用其他方法求它的方程吗?
另解:因为椭圆的焦点在x轴上,所以设它
的标准方程为:
①
②
联立①②,
因此, 所求椭圆的标准方程为:
又∵焦点的坐标为
写出适合下列条件的椭圆的标准方程:
(1) a=4,b=1,焦点在x轴上;
(2)两个焦点的坐标分别是(0,-4)、(0,4),椭圆上一点P到两焦点距离的和等于10
解题反思
求椭圆标准方程的解题步骤:
1.定焦点位置
2.设椭圆方程
3.求a、b的值
4.写出椭圆的标准方程.
变式训练2
1、学到了哪些知识?
一个定义;两类方程;三个字母。
2、巩固了哪些数学方法?
用坐标法求椭圆标准方程
3、运用了什么数学思想?
数形结合 化归思想
课堂小结
必做题:课本42页习题 1、2 ,49页A组第2题
选做题 :练习册27页典例1
作业布置
课后思考
宝剑锋从磨砺出
梅花香自苦寒来
习总书记说:航天梦是强国梦的组成部分,
随着中国航天事业的快速发展,中国人探
索太空的脚步会迈的更大、更远!
2.2.1椭圆及其标准方程
圆的定义:到定点的距离等于定长的点的轨迹
温故而知新
(1)取一条细绳zxxk
(2)把它的两端固定在板上的两点F1、F2
(3)用铅笔尖(M)把细绳拉紧,在板上慢慢移动看看画出的图形
学生实验
思考:1.那些量发生了变化,那些量没有变?
2.有定点,是什么?
3.有定长吗,是什么?
4.动点满足的关系式?
动画演示 形象直观
1、椭圆的定义:
平面内到两个定点F1、F2的距离之和等于常数
的动点M的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距。即|F1F2|
M
2、椭圆定义式:|MF1| + |MF2| = 常数(> |F1F2|)则M点的轨迹是椭圆.
(大于|F1F2|)
总结实验结论
F1
F2
M
若绳长小于 |F1F2| ,则轨迹为____。
若绳长等于 |F1F2|,则轨迹为____。
线段
不存在
M
M
①若|MF1| + |MF2| = 常数 = |F1F2| ,
则M点的轨迹是线段F1F2.
②若|MF1| + |MF2| = 常数< |F1F2| ,
则M点的轨迹不存在.
3、注意事项:
“为何‘常数’要大于两定点间的距离呢?等于、小于又如何呢?”
1.两点间距离公式:
2.求曲线方程的基本步骤:
1、建系
2、设动点
3、限制条件
4、代方程
5、化简
预备知识回顾:
标准方程的推导
? 探讨建立平面直角坐标系的方案
建立平面直角坐标系通常遵循的原则:“对称”、“简洁”
O
x
y
M
F1
F2
方案一
O
x
y
方案二
F1
F2
M
F1
F2
x
y
M( x , y )
F1
F2
x
y
M( x , y )
椭圆上的点M满足|MF1|+|MF2|为定值,
设定值为2a, ︳F1F2︱=2c ,且2a>2c
即:
O
标准方程的推导
即:
则|MF1|+|MF2|=2a
观察左图, 你能从中找出表示 c 、 a 的线段吗? a2-c2 有什么几何意义?
这是焦点在 x 轴上的椭圆的标准方程。
则方程可化为
思考
?
当椭圆的焦点在y轴上时,它的标准方程是怎样 的呢?
想一想
①
②
标准方程中,分母哪个大,焦点就在哪个轴上!
标 准 方 程
相 同 点
焦点位置的判断
不 同 点
图 形
焦 点 坐 标
a、b、c 的关系
焦点在x轴上
焦点在y轴上
y
x
M
O
F1
F2
例1 (1)椭圆
中a=
____,
b=
___,
C=
___.
10
6
8
变式训练1: 若椭圆的方程为
则a= , b= ,c= .
运用新知,解决问题
椭圆标准方程中 和 对应的分母哪个大,
则焦点在哪个轴上.
解题反思
例2 已知椭圆的两个焦点坐标分别是(-2,0),
(2,0), 并且经过点 .求它的标准方程.
解:因为椭圆的焦点在x轴上,所以设
它的标准方程为
由椭圆的定义知
巩固提高
又因为 ,所以
因此, 所求椭圆的标准方程为
所以
能用其他方法求它的方程吗?
另解:因为椭圆的焦点在x轴上,所以设它
的标准方程为:
①
②
联立①②,
因此, 所求椭圆的标准方程为:
又∵焦点的坐标为
写出适合下列条件的椭圆的标准方程:
(1) a=4,b=1,焦点在x轴上;
(2)两个焦点的坐标分别是(0,-4)、(0,4),椭圆上一点P到两焦点距离的和等于10
解题反思
求椭圆标准方程的解题步骤:
1.定焦点位置
2.设椭圆方程
3.求a、b的值
4.写出椭圆的标准方程.
变式训练2
1、学到了哪些知识?
一个定义;两类方程;三个字母。
2、巩固了哪些数学方法?
用坐标法求椭圆标准方程
3、运用了什么数学思想?
数形结合 化归思想
课堂小结
必做题:课本42页习题 1、2 ,49页A组第2题
选做题 :练习册27页典例1
作业布置
课后思考
宝剑锋从磨砺出
梅花香自苦寒来
