2018-2019学年安徽省合肥市瑶海区九年级(上)期末数学试卷解析版
文档属性
| 名称 | 2018-2019学年安徽省合肥市瑶海区九年级(上)期末数学试卷解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 297.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-19 12:57:22 | ||
图片预览



文档简介
2018-2019学年安徽省合肥市瑶海区九年级(上)期末数学试卷
一、选择题(本大题共10小题,每小题4分,共40分)
1.(4分)已知2x=3y,则下列比例式成立的是( )
A.= B.= C.= D.=
2.(4分)抛物线y=﹣2(x﹣3)2﹣4的顶点坐标( )
A.(﹣3,4) B.(﹣3,﹣4) C.(3,﹣4) D.(3,4)
3.(4分)如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,则sinA等于( )
A. B. C. D.
4.(4分)如图,已知点C在弧AB上,∠AOB=110°,则∠ACB的度数为( )
A.55° B.110° C.120° D.125°
5.(4分)如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°﹣α B.α C.180°﹣α D.2α
6.(4分)如图,⊙O是△ABC的内切圆,若∠A=70°,则∠BOC=( )
A.125° B.115° C.100° D.130°
7.(4分)如图,在⊙O中,AE是直径,半径OC垂直于弦AB于D,连接BE,若AB=2,CD=1,则BE的长是( )
A.5 B.6 C.7 D.8
8.(4分)已知抛物线C的解析式为y=ax2+bx+c,则下列说法中错误的是( )
A.a确定抛物线的开口方向与大小
B.若将抛物线C沿y轴平移,则a,b的值不变
C.若将抛物线C沿x轴平移,则a的值不变
D.若将抛物线C沿直线l:y=x+2平移,则a、b、c的值全变
9.(4分)如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则的值为( )
A.1 B. C.1 D.
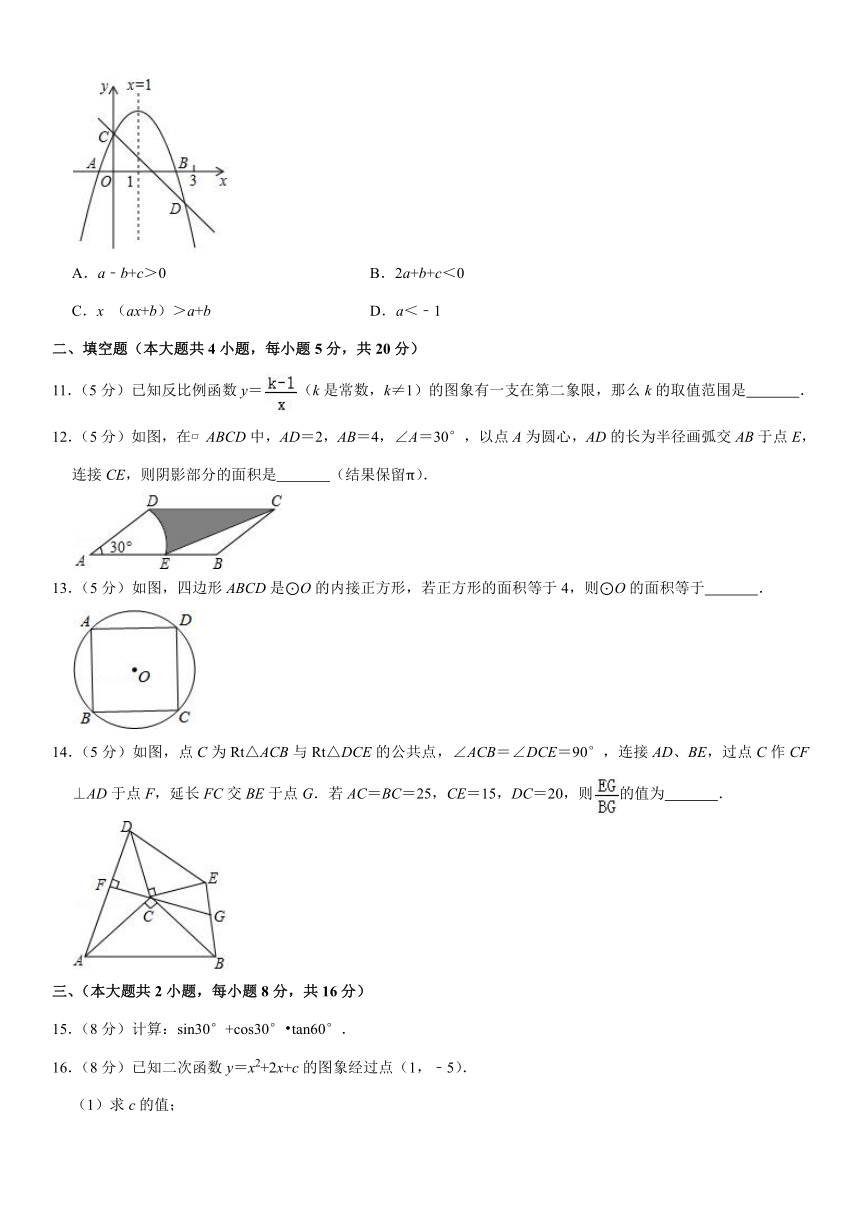
10.(4分)如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A,B两点,与y轴交于点C,对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C,D两点,D点在x轴下方且横坐标小于3,则下列结论中正确的是( )
A.a﹣b+c>0 B.2a+b+c<0
C.x (ax+b)>a+b D.a<﹣1
二、填空题(本大题共4小题,每小题5分,共20分)
11.(5分)已知反比例函数y=(k是常数,k≠1)的图象有一支在第二象限,那么k的取值范围是 .
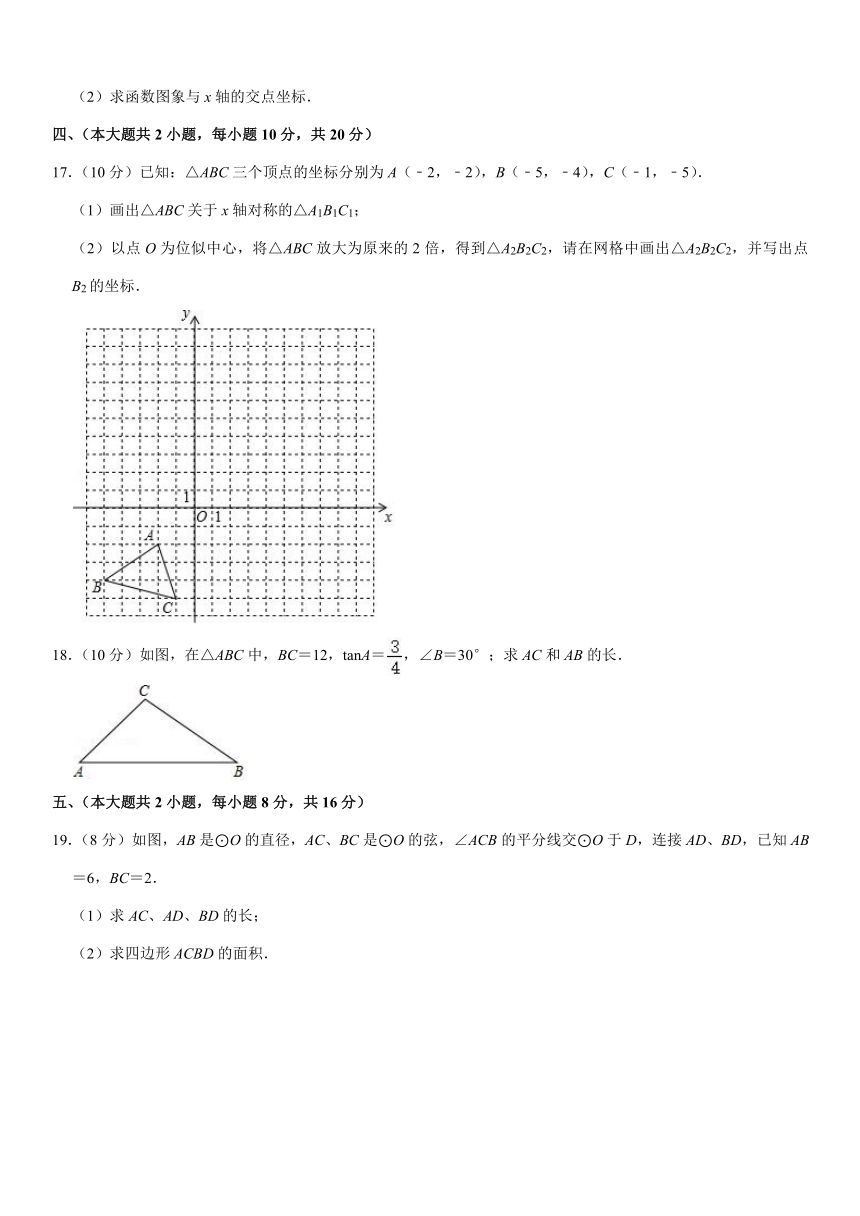
12.(5分)如图,在?ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是 (结果保留π).
13.(5分)如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,则⊙O的面积等于 .
14.(5分)如图,点C为Rt△ACB与Rt△DCE的公共点,∠ACB=∠DCE=90°,连接AD、BE,过点C作CF⊥AD于点F,延长FC交BE于点G.若AC=BC=25,CE=15,DC=20,则的值为 .
三、(本大题共2小题,每小题8分,共16分)
15.(8分)计算:sin30°+cos30°?tan60°.
16.(8分)已知二次函数y=x2+2x+c的图象经过点(1,﹣5).
(1)求c的值;
(2)求函数图象与x轴的交点坐标.
四、(本大题共2小题,每小题10分,共20分)
17.(10分)已知:△ABC三个顶点的坐标分别为A(﹣2,﹣2),B(﹣5,﹣4),C(﹣1,﹣5).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以点O为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2,并写出点B2的坐标.
18.(10分)如图,在△ABC中,BC=12,tanA=,∠B=30°;求AC和AB的长.
五、(本大题共2小题,每小题8分,共16分)
19.(8分)如图,AB是⊙O的直径,AC、BC是⊙O的弦,∠ACB的平分线交⊙O于D,连接AD、BD,已知AB=6,BC=2.
(1)求AC、AD、BD的长;
(2)求四边形ACBD的面积.
20.(8分)某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示)
(I)根据图象,求一次函数y=kx+b的解析式,并写出自变量x的取值范围;
(Ⅱ)该公司要想每天获得最大的利润,应把销售单价定为多少?最大利润值为多少?
六、(本题满分12分)
21.(12分)如图,AB是⊙O的直径,点C为⊙O上一点,CN为⊙O的切线,OM⊥AB于点O,分别交AC、CN于D、M两点.
(1)求证:MD=MC;
(2)若⊙O的半径为5,AC=4,求OD长;
(3)在(2)的基础上求MC长.
七、(本题满分12分)
22.(12分)如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=x刻画.
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.
八、(本题满分14分)
23.(14分)如图①,在锐角△ABC中,D,E分别为AB,BC中点,F为AC上一点,且∠AFE=∠A,DM∥EF交AC于点M.
(1)求证:DM=DA;
(2)点G在BE上,且∠BDG=∠C,如图②,求证:△DEG∽△ECF;
(3)在图②中,(2)的基础上,取CE上一点H,使∠CFH=∠B,若BG=1,求EH的长.
2018-2019学年安徽省合肥市瑶海区九年级(上)期末数学试卷
参考答案与试题解析
一、选择题(本大题共10小题,每小题4分,共40分)
1.【解答】解:A、变成等积式是:xy=6,故错误;
B、变成等积式是:3x=2y,故错误;
C、变成等积式是:2x=3y,故正确;
D、变成等积式是:3x=2y,故错误.
故选:C.
2.【解答】解:∵y=﹣2(x﹣3)2﹣4是抛物线的顶点式,
∴顶点坐标为(3,﹣4).
∴则答案为C
故选:C.
3.【解答】解:在Rt△ABC中,∵AB=10、AC=8,
∴BC===6,
∴sinA===,
故选:A.
4.【解答】解:如图,在优弧上取一点D,连接AD、BD,
∵∠AOB=110°,
∴∠ADB=AOB=55°,
∵A、D、B、C四点共圆,
∴∠ACB+∠ADB=180°,
∴∠ACB=180°﹣55°=125°,
故选:D.
5.【解答】解:由题意可得,
∠CBD=α,∠ACB=∠EDB,
∵∠EDB+∠ADB=180°,
∴∠ADB+∠ACB=180°,
∵∠ADB+∠DBC+∠BCA+∠CAD=360°,∠CBD=α,
∴∠CAD=180°﹣α,
故选:C.
6.【解答】解:∵⊙O是△ABC的内切圆,
∴OB平分∠ABC,OC平分∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣∠A),
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(180°﹣∠A)=90°+∠A=180°+×70°=125°.
故选:A.
7.【解答】解:∵半径OC垂直于弦AB,
∴AD=DB=AB=,
在Rt△AOD中,OA2=(OC﹣CD)2+AD2,即OA2=(OA﹣1)2+()2,
解得,OA=4
∴OD=OC﹣CD=3,
∵AO=OE,AD=DB,
∴BE=2OD=6,
故选:B.
8.【解答】解:A、a确定抛物线的开口方向与大小,所以A选项的说法正确;
B、若将抛物线C沿y轴平移,则抛物线的对称轴不变,开口大小、开口方向不变,所以a,b的值不变,所以B选项的说法正确;
C、若将抛物线C沿x轴平移,抛物线的开口大小、开口方向不变,即a的值不变,所以C选项的说法正确;
D、若将抛物线C沿直线l:y=x+2平移,则a不变,b、c的值改变,所以D选项的说法不正确.
故选:D.
9.【解答】解:∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∴()2=.
∵S△ADE=S四边形BCED,
∴=,
∴===﹣1.
故选:C.
10.【解答】解:∵抛物线与y轴的交点在x轴上方,
∴c>0,
∵抛物线的对称轴为直线x=﹣=1,
∴b=﹣2a,
∴2a+b+c=2a﹣2a+c=c>0,所以B错误;
∵抛物线与x轴的一个交点在点(3,0)左侧,
而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点在点(﹣1,0)右侧,
∴当x=﹣1时,y<0,
∴a﹣b+c<0,所以A错误;
∵x=1时,二次函数有最大值,
∴ax2+bx+c≤a+b+c,
∴ax2+bx≤a+b,所以C错误;
∵直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,
∴x=3时,一次函数值比二次函数值大,
即9a+3b+c<﹣3+c,
而b=﹣2a,
∴9a﹣6a<﹣3,解得a<﹣1,所以D正确.
故选:D.
二、填空题(本大题共4小题,每小题5分,共20分)
11.【解答】解:∵反比例函数y=的图象有一支在第二象限,
∴k﹣1<0,
解得k<1.
故答案为:k<1.
12.【解答】解:过D点作DF⊥AB于点F.
∵AD=2,AB=4,∠A=30°,
∴DF=AD?sin30°=1,EB=AB﹣AE=2,
∴阴影部分的面积:
4×1﹣﹣2×1÷2
=4﹣π﹣1
=3﹣π.
故答案为:3﹣π.
13.【解答】解:正方形的边长AB=2,
则半径是2×=,
则面积是()2π=2π.
故答案是:2π.
14.【解答】解:如图,过E作EH⊥GF于H,过B作BP⊥GF于P,则∠EHG=∠BPG=90°,
又∵∠EGH=∠BGP,
∴△EHG∽△BPG,
∴=,
∵CF⊥AD,
∴∠DFC=∠AFC=90°,
∴∠DFC=∠CHE,∠AFC=∠CPB,
又∵∠ACB=∠DCE=90°,
∴∠CDF=∠ECH,∠FAC=∠PCB,
∴△DCF∽△CEH,△ACF∽△CBP,
∴==,==1,
∴EH=CF,BP=CF,
∴=,
∴=,
故答案为:.
三、(本大题共2小题,每小题8分,共16分)
15.【解答】解:原式=+×
=+
=2.
16.【解答】解:(1)∵点(1,﹣5)在y=x2+2x+c的图象上,
∴﹣5=1+2+c,
∴c=﹣8.
答:c的值为﹣8.
(2)由(1)得函数的解析式为y=x2+2x﹣8,
令y=0,则x2+2x﹣8=0,
解方程得:x1=﹣4,x2=2.
故函数与轴的交点坐标为(﹣4,0),(2,0).
四、(本大题共2小题,每小题10分,共20分)
17.【解答】解:(1)如图所示:△A1B1C1即为所求:
(2)如图所示:△A2B2C2即为所求; B2(10,8)
18.【解答】解:如图作CH⊥AB于H.
在Rt△BCH中,∵BC=12,∠B=30°,
∴CH=BC=6,BH==6,
在Rt△ACH中,tanA==,
∴AH=8,
∴AC==10,
∴AB=AH+BH=8+6.
五、(本大题共2小题,每小题8分,共16分)
19.【解答】解:(1)∵AB是⊙O的直径,
∴∠ACB=∠ACD=90°,
由勾股定理得,AC==4,
∵∠ACB的平分线交⊙O于D,
∴=,
∴AD=BD=×AB=3;
(2)四边形ACBD的面积=×AD×BD+×BC×AC=9+4.
20.【解答】解:(Ⅰ)由函数的图象得:,
解得:,
∴所以y=﹣x+100(50≤x≤80);
(Ⅱ)设每天获得的利润为W元,
由(Ⅰ)得:W=(x﹣50)y=(x﹣50)(﹣x+100)=﹣x2+150x﹣5000=﹣(x﹣75)2+625,
∵﹣1<0,
∴当x=75时,W最大=625即该公司要想第天获得最大利润,应把销售单价为75元/件,最大利润为625元.
六、(本题满分12分)
21.【解答】(1)证明:连接OC,如图所示:
∵CN为⊙O的切线,
∴OC⊥CM,∠OCA+∠ACM=90°,
∵OM⊥AB,
∴∠OAC+∠ODA=90°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠ACM=∠ODA=∠CDM,
∴MD=MC;
(2)解:由题意可知AB=5×2=10,AC=4,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴BC==2,
∵∠AOD=∠ACB,∠A=∠A,
∴△AOD∽△ACB,
∴=,
即=,
可得:OD=2.5,
(3)解:设MC=MD=x,
在Rt△OCM中,由勾股定理得:(x+2.5)2=x2+52,
解得:x=,
即MC=.
七、(本题满分12分)
22.【解答】解:(1)由题意得,y=﹣x2+4x=﹣(x﹣2)2+4,
故二次函数图象的最高点P的坐标为(2,4);
(2)联立两解析式可得:,
解得:,或.
故可得点A的坐标为(,);
(3)如图,作PQ⊥x轴于点Q,AB⊥x轴于点B.
S△POA=S△POQ+S梯形PQBA﹣S△BOA
=×2×4+×(+4)×(﹣2)﹣××
=4+﹣
=;
(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,则△MOA的面积等于△POA的面积.
设直线PM的解析式为y=x+b,
∵P的坐标为(2,4),
∴4=×2+b,解得b=3,
∴直线PM的解析式为y=x+3.
由,解得,,
∴点M的坐标为(,).
八、(本题满分14分)
23.【解答】(1)证明:如图1所示,
∵DM∥EF,
∴∠AMD=∠AFE,
∵∠AFE=∠A,
∴∠AMD=∠A,
∴DM=DA;
(2)证明:如图2所示,
∵D、E分别是AB、BC的中点,
∴DE∥AC,
∴∠BDE=∠A,∠DEG=∠C,
∵∠AFE=∠A,
∴∠BDE=∠AFE,
∴∠BDG+∠GDE=∠C+∠FEC,
∵∠BDG=∠C,
∴∠GDE=∠FEC,
∴△DEG∽△ECF;
(3)解:如图3所示,
∵∠BDG=∠C=∠DEB,∠B=∠B,
∴△BDG∽△BED,
∴,
∴BD2=BG?BE,
∵∠AFE=∠A,∠CFH=∠B,
∴∠C=180°﹣∠A﹣∠B=180°﹣∠AFE﹣∠CFH=∠EFH,
又∵∠FEH=∠CEF,
∴△EFH∽△ECF,
∴,
∴EF2=EH?EC,
∵DE∥AC,DM∥EF,
∴四边形DEFM是平行四边形,
∴EF=DM=DA=BD,
∴BG?BE=EH?EC,
∵BE=EC,
∴EH=BG=1.
一、选择题(本大题共10小题,每小题4分,共40分)
1.(4分)已知2x=3y,则下列比例式成立的是( )
A.= B.= C.= D.=
2.(4分)抛物线y=﹣2(x﹣3)2﹣4的顶点坐标( )
A.(﹣3,4) B.(﹣3,﹣4) C.(3,﹣4) D.(3,4)
3.(4分)如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,则sinA等于( )
A. B. C. D.
4.(4分)如图,已知点C在弧AB上,∠AOB=110°,则∠ACB的度数为( )
A.55° B.110° C.120° D.125°
5.(4分)如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°﹣α B.α C.180°﹣α D.2α
6.(4分)如图,⊙O是△ABC的内切圆,若∠A=70°,则∠BOC=( )
A.125° B.115° C.100° D.130°
7.(4分)如图,在⊙O中,AE是直径,半径OC垂直于弦AB于D,连接BE,若AB=2,CD=1,则BE的长是( )
A.5 B.6 C.7 D.8
8.(4分)已知抛物线C的解析式为y=ax2+bx+c,则下列说法中错误的是( )
A.a确定抛物线的开口方向与大小
B.若将抛物线C沿y轴平移,则a,b的值不变
C.若将抛物线C沿x轴平移,则a的值不变
D.若将抛物线C沿直线l:y=x+2平移,则a、b、c的值全变
9.(4分)如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则的值为( )
A.1 B. C.1 D.
10.(4分)如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A,B两点,与y轴交于点C,对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C,D两点,D点在x轴下方且横坐标小于3,则下列结论中正确的是( )
A.a﹣b+c>0 B.2a+b+c<0
C.x (ax+b)>a+b D.a<﹣1
二、填空题(本大题共4小题,每小题5分,共20分)
11.(5分)已知反比例函数y=(k是常数,k≠1)的图象有一支在第二象限,那么k的取值范围是 .
12.(5分)如图,在?ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是 (结果保留π).
13.(5分)如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,则⊙O的面积等于 .
14.(5分)如图,点C为Rt△ACB与Rt△DCE的公共点,∠ACB=∠DCE=90°,连接AD、BE,过点C作CF⊥AD于点F,延长FC交BE于点G.若AC=BC=25,CE=15,DC=20,则的值为 .
三、(本大题共2小题,每小题8分,共16分)
15.(8分)计算:sin30°+cos30°?tan60°.
16.(8分)已知二次函数y=x2+2x+c的图象经过点(1,﹣5).
(1)求c的值;
(2)求函数图象与x轴的交点坐标.
四、(本大题共2小题,每小题10分,共20分)
17.(10分)已知:△ABC三个顶点的坐标分别为A(﹣2,﹣2),B(﹣5,﹣4),C(﹣1,﹣5).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以点O为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2,并写出点B2的坐标.
18.(10分)如图,在△ABC中,BC=12,tanA=,∠B=30°;求AC和AB的长.
五、(本大题共2小题,每小题8分,共16分)
19.(8分)如图,AB是⊙O的直径,AC、BC是⊙O的弦,∠ACB的平分线交⊙O于D,连接AD、BD,已知AB=6,BC=2.
(1)求AC、AD、BD的长;
(2)求四边形ACBD的面积.
20.(8分)某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示)
(I)根据图象,求一次函数y=kx+b的解析式,并写出自变量x的取值范围;
(Ⅱ)该公司要想每天获得最大的利润,应把销售单价定为多少?最大利润值为多少?
六、(本题满分12分)
21.(12分)如图,AB是⊙O的直径,点C为⊙O上一点,CN为⊙O的切线,OM⊥AB于点O,分别交AC、CN于D、M两点.
(1)求证:MD=MC;
(2)若⊙O的半径为5,AC=4,求OD长;
(3)在(2)的基础上求MC长.
七、(本题满分12分)
22.(12分)如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=x刻画.
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.
八、(本题满分14分)
23.(14分)如图①,在锐角△ABC中,D,E分别为AB,BC中点,F为AC上一点,且∠AFE=∠A,DM∥EF交AC于点M.
(1)求证:DM=DA;
(2)点G在BE上,且∠BDG=∠C,如图②,求证:△DEG∽△ECF;
(3)在图②中,(2)的基础上,取CE上一点H,使∠CFH=∠B,若BG=1,求EH的长.
2018-2019学年安徽省合肥市瑶海区九年级(上)期末数学试卷
参考答案与试题解析
一、选择题(本大题共10小题,每小题4分,共40分)
1.【解答】解:A、变成等积式是:xy=6,故错误;
B、变成等积式是:3x=2y,故错误;
C、变成等积式是:2x=3y,故正确;
D、变成等积式是:3x=2y,故错误.
故选:C.
2.【解答】解:∵y=﹣2(x﹣3)2﹣4是抛物线的顶点式,
∴顶点坐标为(3,﹣4).
∴则答案为C
故选:C.
3.【解答】解:在Rt△ABC中,∵AB=10、AC=8,
∴BC===6,
∴sinA===,
故选:A.
4.【解答】解:如图,在优弧上取一点D,连接AD、BD,
∵∠AOB=110°,
∴∠ADB=AOB=55°,
∵A、D、B、C四点共圆,
∴∠ACB+∠ADB=180°,
∴∠ACB=180°﹣55°=125°,
故选:D.
5.【解答】解:由题意可得,
∠CBD=α,∠ACB=∠EDB,
∵∠EDB+∠ADB=180°,
∴∠ADB+∠ACB=180°,
∵∠ADB+∠DBC+∠BCA+∠CAD=360°,∠CBD=α,
∴∠CAD=180°﹣α,
故选:C.
6.【解答】解:∵⊙O是△ABC的内切圆,
∴OB平分∠ABC,OC平分∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣∠A),
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(180°﹣∠A)=90°+∠A=180°+×70°=125°.
故选:A.
7.【解答】解:∵半径OC垂直于弦AB,
∴AD=DB=AB=,
在Rt△AOD中,OA2=(OC﹣CD)2+AD2,即OA2=(OA﹣1)2+()2,
解得,OA=4
∴OD=OC﹣CD=3,
∵AO=OE,AD=DB,
∴BE=2OD=6,
故选:B.
8.【解答】解:A、a确定抛物线的开口方向与大小,所以A选项的说法正确;
B、若将抛物线C沿y轴平移,则抛物线的对称轴不变,开口大小、开口方向不变,所以a,b的值不变,所以B选项的说法正确;
C、若将抛物线C沿x轴平移,抛物线的开口大小、开口方向不变,即a的值不变,所以C选项的说法正确;
D、若将抛物线C沿直线l:y=x+2平移,则a不变,b、c的值改变,所以D选项的说法不正确.
故选:D.
9.【解答】解:∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∴()2=.
∵S△ADE=S四边形BCED,
∴=,
∴===﹣1.
故选:C.
10.【解答】解:∵抛物线与y轴的交点在x轴上方,
∴c>0,
∵抛物线的对称轴为直线x=﹣=1,
∴b=﹣2a,
∴2a+b+c=2a﹣2a+c=c>0,所以B错误;
∵抛物线与x轴的一个交点在点(3,0)左侧,
而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点在点(﹣1,0)右侧,
∴当x=﹣1时,y<0,
∴a﹣b+c<0,所以A错误;
∵x=1时,二次函数有最大值,
∴ax2+bx+c≤a+b+c,
∴ax2+bx≤a+b,所以C错误;
∵直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,
∴x=3时,一次函数值比二次函数值大,
即9a+3b+c<﹣3+c,
而b=﹣2a,
∴9a﹣6a<﹣3,解得a<﹣1,所以D正确.
故选:D.
二、填空题(本大题共4小题,每小题5分,共20分)
11.【解答】解:∵反比例函数y=的图象有一支在第二象限,
∴k﹣1<0,
解得k<1.
故答案为:k<1.
12.【解答】解:过D点作DF⊥AB于点F.
∵AD=2,AB=4,∠A=30°,
∴DF=AD?sin30°=1,EB=AB﹣AE=2,
∴阴影部分的面积:
4×1﹣﹣2×1÷2
=4﹣π﹣1
=3﹣π.
故答案为:3﹣π.
13.【解答】解:正方形的边长AB=2,
则半径是2×=,
则面积是()2π=2π.
故答案是:2π.
14.【解答】解:如图,过E作EH⊥GF于H,过B作BP⊥GF于P,则∠EHG=∠BPG=90°,
又∵∠EGH=∠BGP,
∴△EHG∽△BPG,
∴=,
∵CF⊥AD,
∴∠DFC=∠AFC=90°,
∴∠DFC=∠CHE,∠AFC=∠CPB,
又∵∠ACB=∠DCE=90°,
∴∠CDF=∠ECH,∠FAC=∠PCB,
∴△DCF∽△CEH,△ACF∽△CBP,
∴==,==1,
∴EH=CF,BP=CF,
∴=,
∴=,
故答案为:.
三、(本大题共2小题,每小题8分,共16分)
15.【解答】解:原式=+×
=+
=2.
16.【解答】解:(1)∵点(1,﹣5)在y=x2+2x+c的图象上,
∴﹣5=1+2+c,
∴c=﹣8.
答:c的值为﹣8.
(2)由(1)得函数的解析式为y=x2+2x﹣8,
令y=0,则x2+2x﹣8=0,
解方程得:x1=﹣4,x2=2.
故函数与轴的交点坐标为(﹣4,0),(2,0).
四、(本大题共2小题,每小题10分,共20分)
17.【解答】解:(1)如图所示:△A1B1C1即为所求:
(2)如图所示:△A2B2C2即为所求; B2(10,8)
18.【解答】解:如图作CH⊥AB于H.
在Rt△BCH中,∵BC=12,∠B=30°,
∴CH=BC=6,BH==6,
在Rt△ACH中,tanA==,
∴AH=8,
∴AC==10,
∴AB=AH+BH=8+6.
五、(本大题共2小题,每小题8分,共16分)
19.【解答】解:(1)∵AB是⊙O的直径,
∴∠ACB=∠ACD=90°,
由勾股定理得,AC==4,
∵∠ACB的平分线交⊙O于D,
∴=,
∴AD=BD=×AB=3;
(2)四边形ACBD的面积=×AD×BD+×BC×AC=9+4.
20.【解答】解:(Ⅰ)由函数的图象得:,
解得:,
∴所以y=﹣x+100(50≤x≤80);
(Ⅱ)设每天获得的利润为W元,
由(Ⅰ)得:W=(x﹣50)y=(x﹣50)(﹣x+100)=﹣x2+150x﹣5000=﹣(x﹣75)2+625,
∵﹣1<0,
∴当x=75时,W最大=625即该公司要想第天获得最大利润,应把销售单价为75元/件,最大利润为625元.
六、(本题满分12分)
21.【解答】(1)证明:连接OC,如图所示:
∵CN为⊙O的切线,
∴OC⊥CM,∠OCA+∠ACM=90°,
∵OM⊥AB,
∴∠OAC+∠ODA=90°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠ACM=∠ODA=∠CDM,
∴MD=MC;
(2)解:由题意可知AB=5×2=10,AC=4,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴BC==2,
∵∠AOD=∠ACB,∠A=∠A,
∴△AOD∽△ACB,
∴=,
即=,
可得:OD=2.5,
(3)解:设MC=MD=x,
在Rt△OCM中,由勾股定理得:(x+2.5)2=x2+52,
解得:x=,
即MC=.
七、(本题满分12分)
22.【解答】解:(1)由题意得,y=﹣x2+4x=﹣(x﹣2)2+4,
故二次函数图象的最高点P的坐标为(2,4);
(2)联立两解析式可得:,
解得:,或.
故可得点A的坐标为(,);
(3)如图,作PQ⊥x轴于点Q,AB⊥x轴于点B.
S△POA=S△POQ+S梯形PQBA﹣S△BOA
=×2×4+×(+4)×(﹣2)﹣××
=4+﹣
=;
(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,则△MOA的面积等于△POA的面积.
设直线PM的解析式为y=x+b,
∵P的坐标为(2,4),
∴4=×2+b,解得b=3,
∴直线PM的解析式为y=x+3.
由,解得,,
∴点M的坐标为(,).
八、(本题满分14分)
23.【解答】(1)证明:如图1所示,
∵DM∥EF,
∴∠AMD=∠AFE,
∵∠AFE=∠A,
∴∠AMD=∠A,
∴DM=DA;
(2)证明:如图2所示,
∵D、E分别是AB、BC的中点,
∴DE∥AC,
∴∠BDE=∠A,∠DEG=∠C,
∵∠AFE=∠A,
∴∠BDE=∠AFE,
∴∠BDG+∠GDE=∠C+∠FEC,
∵∠BDG=∠C,
∴∠GDE=∠FEC,
∴△DEG∽△ECF;
(3)解:如图3所示,
∵∠BDG=∠C=∠DEB,∠B=∠B,
∴△BDG∽△BED,
∴,
∴BD2=BG?BE,
∵∠AFE=∠A,∠CFH=∠B,
∴∠C=180°﹣∠A﹣∠B=180°﹣∠AFE﹣∠CFH=∠EFH,
又∵∠FEH=∠CEF,
∴△EFH∽△ECF,
∴,
∴EF2=EH?EC,
∵DE∥AC,DM∥EF,
∴四边形DEFM是平行四边形,
∴EF=DM=DA=BD,
∴BG?BE=EH?EC,
∵BE=EC,
∴EH=BG=1.
同课章节目录
