六年级数学下册课件 - - 6.2.1 图形的认识与测量-立体图形 -人教新课标 (共21张PPT)
文档属性
| 名称 | 六年级数学下册课件 - - 6.2.1 图形的认识与测量-立体图形 -人教新课标 (共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 915.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-18 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
立体图形总复习练习
教学目标:
知识与技能 认识学过的一些立体图形特征,掌握不 同立体图形之间的异同。
过程与方法 能够灵活应用所学过的立体图形的特征解决简单实际问题。
情感态度与价值观 发展空间观念
预习交流:
小游戏“我说你猜”。(请你根据我的描述?猜测一下?可能是什么立体图形,看谁反映最快。 )
有6个面?其中一个面是长方形。
有6个面?其中一个面是正方形。
我摸到一个曲面?还摸到一个平面圆。
我还是摸到一个曲面,哟扎我的手。
可能是长方体
可能是正方体
可能是圆柱
可能是圆锥体
① 一个长方体最多有两个正方形。( )
② 圆柱的侧面展开不是正方形就是长方形。
( )
③ 长方体的三条棱就是它的长、宽、高。
( )
④ 圆锥的高有一条,圆柱的高有两条。
( )
√
×
×
×
预习交流:
判断并说明理由
(1)做一个长方体铁皮罐头盒,求需要多少铁皮,是求它的( ),罐头盒周围贴商标纸,求商标纸的面积是求它的( )。
(2)做一只圆柱形通风管要用多少铁皮,是求它的( )。
(3) 一个圆柱形水池占地多少平方米,是求圆柱的( )。
表面积
侧面积 (侧面4个面的面积)
侧面积
底面积
预习交流:
1.如下图,有三块不同的硬纸片,让它们分别绕PQ边旋转一周,它们所掠边的空间是圆锥体的是( ).
P
Q
P
Q
P
Q
B
A
C
B
重难突破:
2cm
(40- 5×4+3×4)÷4=2cm
重难突破:
2. 一个长方体的棱长总和是40厘米,其中长5厘米,宽3厘米,高是多少厘米. ( ).
3.一个圆锥的体积是a立方米,和它等底等高的圆柱体的体积是( )立方米。
A. a÷3 B. 2a 1 C. 3a D. a的立方
C
重难突破:
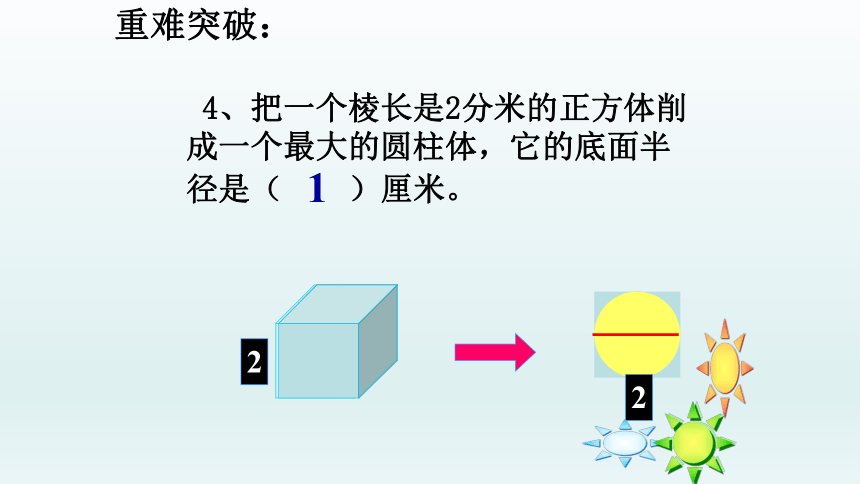
4、把一个棱长是2分米的正方体削成一个最大的圆柱体,它的底面半径是( )厘米。
2
2
1
重难突破:
1
2
3
4
5
底面
后面
前面
左面
右面
h
h
h
h
h
h
h
h
5.用右边五块玻璃片做一个金鱼缸。请你指出哪一块是鱼缸底面,哪些是侧面,并在侧面的玻璃片上标出这个鱼缸的高h。
这个鱼缸的长、宽、高分别是100厘米、80厘米和70厘米。请同学们解决下面这个问题
(1)这个鱼缸的占地面积为多少平方米?
100×80=8000cm=0.8m
答:这个鱼缸的占地面积为0.8平方米.
这个鱼缸的长、宽、高分别是100厘米、80厘米和70厘米。请同学们解决下面这个问题
(2)制作这个鱼缸需要多少平方分米的玻璃?
(100×80+100×70+80×70)×2=412(平方分米)
答:制作这个鱼缸需要412平方分米的玻璃。
这个鱼缸的长、宽、高分别是100厘米、80厘米和70厘米。请同学们解决下面这个问题
(3)在放入小鱼前水深为50厘米放入小鱼后水深为51厘米,求小鱼的体积?
100×80×(51-50)=8000(立方厘米)
答:小鱼的体积为8000立方厘米。
6. 做一个底面半径是2厘米,高是5厘米的无盖圆柱形铁盒,至少需要多少铁皮?
=12.56+62.8
=75.36(平方厘米)
答:至少需要75.36平方厘米铁皮。
3.14×2 +3.14×2×2×5
2
重难突破:
7、 把一根长3m,底面直径2 dm的圆柱形钢管截3段,表面积增加了多少?
重难突破:
小壁虎的难题:
如图:一只圆桶的下方有一只壁虎,上方有一只蚊子,壁虎要想尽快吃到蚊子,应该走哪条路径?
你有何高招?
● 蚊子
壁虎 ●
重难突破:
蚊子
●
●
壁虎
● 蚊子
壁虎 ●
生活中的数学问题
1、 一个圆锥形状的土堆,底面周长314米,高1.5米。这堆土有多少立方米?
3.14×502×1.5×
=3.14×1250
=3925(立方米)
314÷3.14÷2=50(米)
达标提升
生活中的数学问题
2、一个用塑料薄膜覆盖的草莓大棚,长15米,横截面是一个半径2米的半圆。
①大棚内的空间有多少大?
3.14×22×15÷2
=3.14×4×15÷2
=3.14×30
=94.2(立方米)
答:大棚内的空间为94.2立方米。
达标提升
生活中的数学问题
2、一个用塑料薄膜覆盖的蔬菜大棚,长15米,横截面是一个半径2米的半圆。
②覆盖在这个大棚上的塑料薄膜约有多少平方米?
3.14×22+3.14×22×15÷2
=3.14×(4+30)
=3.14×34
=106.76(平方米)
答:覆盖在这个大棚上的塑料薄膜约有106.76平方米.
达标提升
同学们通过今天的学习你有什么收获?
立体图形总复习练习
教学目标:
知识与技能 认识学过的一些立体图形特征,掌握不 同立体图形之间的异同。
过程与方法 能够灵活应用所学过的立体图形的特征解决简单实际问题。
情感态度与价值观 发展空间观念
预习交流:
小游戏“我说你猜”。(请你根据我的描述?猜测一下?可能是什么立体图形,看谁反映最快。 )
有6个面?其中一个面是长方形。
有6个面?其中一个面是正方形。
我摸到一个曲面?还摸到一个平面圆。
我还是摸到一个曲面,哟扎我的手。
可能是长方体
可能是正方体
可能是圆柱
可能是圆锥体
① 一个长方体最多有两个正方形。( )
② 圆柱的侧面展开不是正方形就是长方形。
( )
③ 长方体的三条棱就是它的长、宽、高。
( )
④ 圆锥的高有一条,圆柱的高有两条。
( )
√
×
×
×
预习交流:
判断并说明理由
(1)做一个长方体铁皮罐头盒,求需要多少铁皮,是求它的( ),罐头盒周围贴商标纸,求商标纸的面积是求它的( )。
(2)做一只圆柱形通风管要用多少铁皮,是求它的( )。
(3) 一个圆柱形水池占地多少平方米,是求圆柱的( )。
表面积
侧面积 (侧面4个面的面积)
侧面积
底面积
预习交流:
1.如下图,有三块不同的硬纸片,让它们分别绕PQ边旋转一周,它们所掠边的空间是圆锥体的是( ).
P
Q
P
Q
P
Q
B
A
C
B
重难突破:
2cm
(40- 5×4+3×4)÷4=2cm
重难突破:
2. 一个长方体的棱长总和是40厘米,其中长5厘米,宽3厘米,高是多少厘米. ( ).
3.一个圆锥的体积是a立方米,和它等底等高的圆柱体的体积是( )立方米。
A. a÷3 B. 2a 1 C. 3a D. a的立方
C
重难突破:
4、把一个棱长是2分米的正方体削成一个最大的圆柱体,它的底面半径是( )厘米。
2
2
1
重难突破:
1
2
3
4
5
底面
后面
前面
左面
右面
h
h
h
h
h
h
h
h
5.用右边五块玻璃片做一个金鱼缸。请你指出哪一块是鱼缸底面,哪些是侧面,并在侧面的玻璃片上标出这个鱼缸的高h。
这个鱼缸的长、宽、高分别是100厘米、80厘米和70厘米。请同学们解决下面这个问题
(1)这个鱼缸的占地面积为多少平方米?
100×80=8000cm=0.8m
答:这个鱼缸的占地面积为0.8平方米.
这个鱼缸的长、宽、高分别是100厘米、80厘米和70厘米。请同学们解决下面这个问题
(2)制作这个鱼缸需要多少平方分米的玻璃?
(100×80+100×70+80×70)×2=412(平方分米)
答:制作这个鱼缸需要412平方分米的玻璃。
这个鱼缸的长、宽、高分别是100厘米、80厘米和70厘米。请同学们解决下面这个问题
(3)在放入小鱼前水深为50厘米放入小鱼后水深为51厘米,求小鱼的体积?
100×80×(51-50)=8000(立方厘米)
答:小鱼的体积为8000立方厘米。
6. 做一个底面半径是2厘米,高是5厘米的无盖圆柱形铁盒,至少需要多少铁皮?
=12.56+62.8
=75.36(平方厘米)
答:至少需要75.36平方厘米铁皮。
3.14×2 +3.14×2×2×5
2
重难突破:
7、 把一根长3m,底面直径2 dm的圆柱形钢管截3段,表面积增加了多少?
重难突破:
小壁虎的难题:
如图:一只圆桶的下方有一只壁虎,上方有一只蚊子,壁虎要想尽快吃到蚊子,应该走哪条路径?
你有何高招?
● 蚊子
壁虎 ●
重难突破:
蚊子
●
●
壁虎
● 蚊子
壁虎 ●
生活中的数学问题
1、 一个圆锥形状的土堆,底面周长314米,高1.5米。这堆土有多少立方米?
3.14×502×1.5×
=3.14×1250
=3925(立方米)
314÷3.14÷2=50(米)
达标提升
生活中的数学问题
2、一个用塑料薄膜覆盖的草莓大棚,长15米,横截面是一个半径2米的半圆。
①大棚内的空间有多少大?
3.14×22×15÷2
=3.14×4×15÷2
=3.14×30
=94.2(立方米)
答:大棚内的空间为94.2立方米。
达标提升
生活中的数学问题
2、一个用塑料薄膜覆盖的蔬菜大棚,长15米,横截面是一个半径2米的半圆。
②覆盖在这个大棚上的塑料薄膜约有多少平方米?
3.14×22+3.14×22×15÷2
=3.14×(4+30)
=3.14×34
=106.76(平方米)
答:覆盖在这个大棚上的塑料薄膜约有106.76平方米.
达标提升
同学们通过今天的学习你有什么收获?
