上海市闵行区2019-2020学年第一学期九年级期末考试数学试卷(word版含答案)
文档属性
| 名称 | 上海市闵行区2019-2020学年第一学期九年级期末考试数学试卷(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 540.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-18 00:00:00 | ||
图片预览


文档简介
闵行区2019学年第一学期九年级质量监控考试
数 学 试 卷
(考试时间100分钟,满分150分)
考生注意:
1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.
2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.
3.本次测试可使用科学计算器.
一、选择题:(本大题共6题,每题4分,满分24分)
【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确选项的代号并填涂在答题纸的相应位置上】
1.如果把Rt△ABC的各边长都扩大到原来的n倍,那么锐角A的四个三角比值
(A)都缩小到原来的n倍; (B)都扩大到原来的n倍;
(C)都没有变化; (D)不同三角比的变化不一致.
2.已知P是线段AB的黄金分割点,且AP > BP,那么下列比例式能成立的是
(A); (B); (C); (D).
3.k为任意实数,抛物线的顶点总在
(A)直线上; (B)直线上; (C)x轴上; (D)y轴上.
4.如图在正三角形ABC中,点D、E分别在AC、AB上,且,AE = BE,那么有
(A)△AED∽△BED; (B)△BAD∽△BCD;
(C)△AED∽△ABD; (D)△AED∽△CBD.
5.下列命题是真命题的是
(A)经过平面内任意三点可作一个圆;
(B)相等的圆心角所对的弧一定相等;
(C)相交两圆的公共弦一定垂直于两圆的连心线;
(D)内切两圆的圆心距等于两圆的半径的和.
6.二次函数的图像如图所示,现有以下结论:
①;②;③;④;
其中正确的结论有
(A)1个; (B)2个;
(C)3个; (D)4个.
二、填空题:(本大题共12题,每题4分,满分48分)
【请将结果直接填入答题纸的相应位置上】
7.已知线段a = 4厘米,c = 9厘米,那么线段a和c的比例中项 ▲ 厘米.
8.在Rt△ABC中,∠C=90?,AB=10,,那么BC = ▲ .
9.抛物线在对称轴右侧的部分是 ▲ 的.(填“上升”或“下降”)
10.如果两个相似三角形的相似比为2︰3,两个三角形的周长的和是100cm,那么较小的三角形的周长为 ▲ cm.
11.为单位向量,与的方向相反,且长度为6,那么= ▲ .
12.某人从地面沿坡度的山坡走了100米,这时他离地面的高度是 ▲ 米.
13.已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在BC的延长线上的点E处,那么= ▲ .
14.已知在Rt△ABC中,∠C=90?,AC=3,BC=4,⊙C与斜边AB相切,那么⊙C的半径为 ▲ .
15.设抛物线l:的顶点为D,与y轴的交点是C,我们称以C为顶点,且过点D的抛物线为抛物线l的“伴随抛物线”,请写出抛物线的伴随抛物线的解析式 ▲ .
16.半径分别为3cm与cm的⊙O1与⊙O2相交于A、B两点,如果公共弦AB=cm,那么圆心距O1O2的长为 ▲ cm.
17.正五边形的边长与边心距的比值为 ▲ .(用含三角比的代数式表示)
18.如图,在等腰△ABC中,AB = AC = 4,BC = 6,点D在底边BC上,且∠DAC =∠ACD,将△ACD沿着AD所在直线翻折,使得点C落到点E处,联结BE,那么BE的长为 ▲ .
三、解答题:(本大题共7题,满分78分)
19.(本题满分10分)
已知二次函数图像的最高点是A(1,4),且经过点B(0,3),与轴交于C、D两点(点C在点D的左侧).求△BCD的面积.
20.(本题共2小题,第(1)小题2分,第(2)小题8分,满分10分)
已知:在平行四边形ABCD中,AB︰BC = 3︰2.
(1)根据条件画图:作∠BCD的平分线,交边AB于点E,
取线段BE的中点F,联结DF交CE于点G.
(2)设=,=,那么向量= ▲ ;
(用向量、表示),并在图中画出向量
在向量和方向上的分向量.
21.(本题共2小题,第(1)小题6分,第(2)小题4分,满分10分)
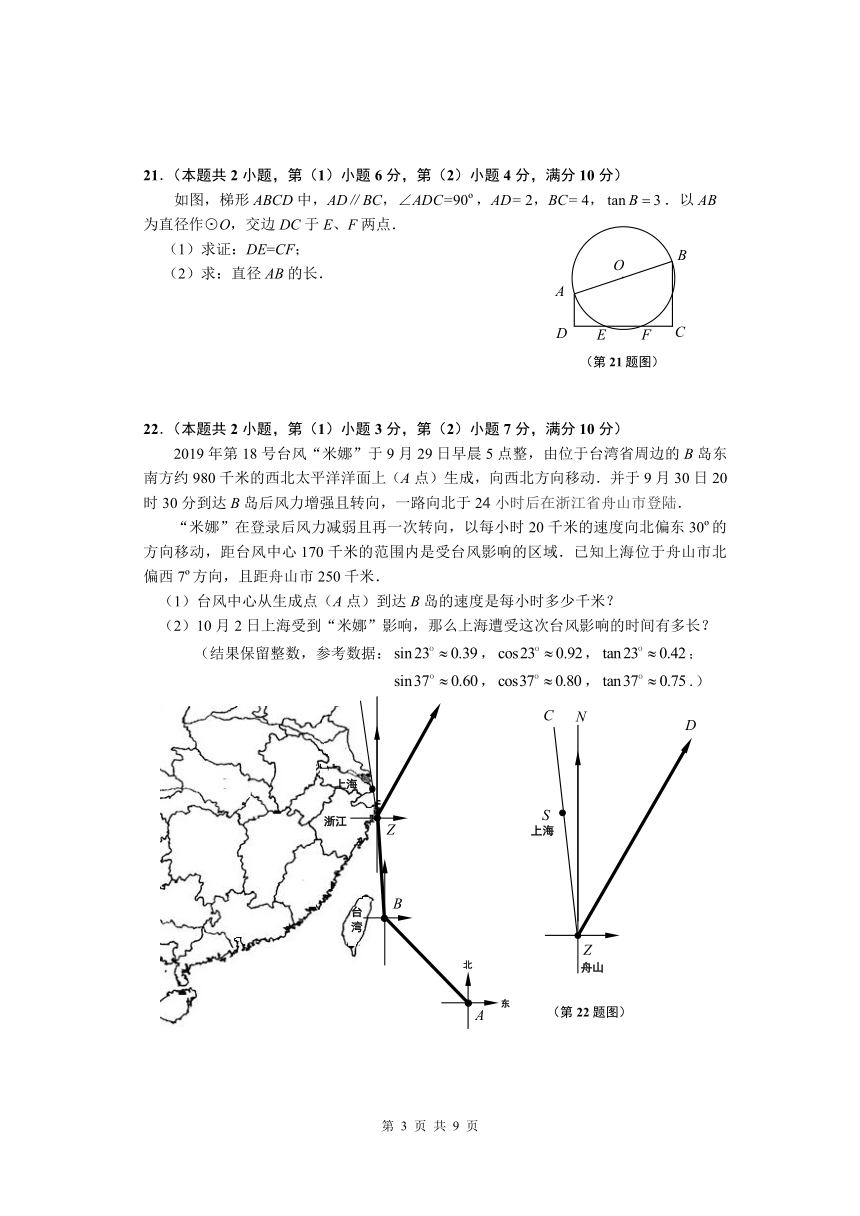
如图,梯形ABCD中,AD∥BC,∠ADC=90?,AD= 2,BC= 4,.以AB为直径作⊙O,交边DC于E、F两点.
(1)求证:DE=CF;
(2)求:直径AB的长.
22.(本题共2小题,第(1)小题3分,第(2)小题7分,满分10分)
2019年第18号台风“米娜”于9月29日早晨5点整,由位于台湾省周边的B岛东南方约980千米的西北太平洋洋面上(A点)生成,向西北方向移动.并于9月30日20时30分到达B岛后风力增强且转向,一路向北于24小时后在浙江省舟山市登陆.
“米娜”在登录后风力减弱且再一次转向,以每小时20千米的速度向北偏东30?的方向移动,距台风中心170千米的范围内是受台风影响的区域.已知上海位于舟山市北偏西7?方向,且距舟山市250千米.
(1)台风中心从生成点(A点)到达B岛的速度是每小时多少千米?
(2)10月2日上海受到“米娜”影响,那么上海遭受这次台风影响的时间有多长?
(结果保留整数,参考数据:,,;
,,.)
23.(本题共2小题,每小题6分,满分12分)
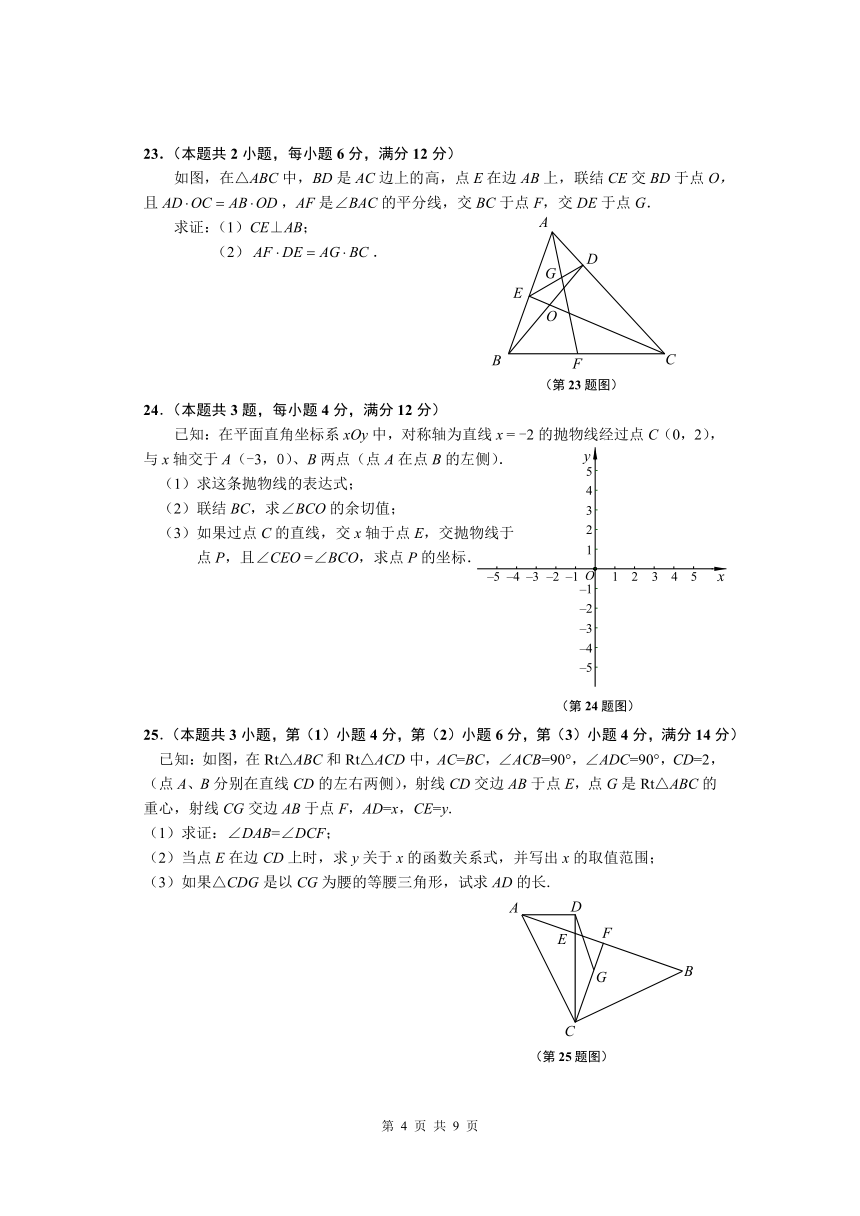
如图,在△ABC中,BD是AC边上的高,点E在边AB上,联结CE交BD于点O,且,AF是∠BAC的平分线,交BC于点F,交DE于点G.
求证:(1)CE⊥AB;
(2).
24.(本题共3题,每小题4分,满分12分)
已知:在平面直角坐标系xOy中,对称轴为直线x = -2的抛物线经过点C(0,2),与x轴交于A(-3,0)、B两点(点A在点B的左侧).
(1)求这条抛物线的表达式;
(2)联结BC,求∠BCO的余切值;
(3)如果过点C的直线,交x轴于点E,交抛物线于
点P,且∠CEO =∠BCO,求点P的坐标.
25.(本题共3小题,第(1)小题4分,第(2)小题6分,第(3)小题4分,满分14分)
已知:如图,在Rt△ABC和Rt△ACD中,AC=BC,∠ACB=90°,∠ADC=90°,CD=2,(点A、B分别在直线CD的左右两侧),射线CD交边AB于点E,点G是Rt△ABC的重心,射线CG交边AB于点F,AD=x,CE=y.
(1)求证:∠DAB=∠DCF;
(2)当点E在边CD上时,求y关于x的函数关系式,并写出x的取值范围;
(3)如果△CDG是以CG为腰的等腰三角形,试求AD的长.
闵行区2019学年第一学期九年级质量监控试卷
答案要点及评分标准
一、选择题:
1.C; 2.A; 3.B; 4.D; 5.C; 6.B.
二、填空题:
7.6; 8.4; 9.下降; 10.40; 11.-6; 12.50; 13.;
14.; 15.; 16.2或4; 17.().; 18.1.
三、解答题:
19.解:设所求的二次函数解析式为,………………………(2分)
把B(0,3)代入得解得:.…………………………(2分)
令,那么,解得:.………………………(2分)
∴CD=4.…………………………………………………………………………(2分)
在△BCD中,·CD·OB=.………………………………(2分)
20.解:(1)角平分线………………………………(1分)
整体画对;……………………………(1分)
(2)=.…………………(4分)
画图及结论正确.……………………(4分)
21.解:(1)过点O作OH⊥DC,垂足为H.
∵AD∥BC,∠ADC=90?,OH⊥DC,
∴∠BCN=∠OHC=∠ADC =90?.……(1分)
∴AD∥OH∥BC.……………………(1分)
又∵OA=OB.……………………………(1分)
∴DH=HC.……………………………(1分)
∵OH⊥DC,OH过圆心,
∴EH = HF.……………………………(1分)
∴DH-EH =HC-HF.………………(1分)
即:DE=CF.
(2)过点A作AG⊥BC,垂足为点G,∠AGB = 90°,
∵∠AGB =∠BCN = 90°,∴AG∥DC.
∵AD∥BC,∴AD=CG.……………………………………………………(1分)
∵AD= 2,BC= 4,∴BG= BC-CG =2.………………………………(1分)
在Rt△AGB中,∵,
∴.……………………………………………(1分)
在Rt△AGB中,
∴AB=.………………………………………………………………(1分)
22.解:(1)由题意得,AB=980千米,台风中心到达B岛的时间是39.5小时.…(1分)
∴(千米).…………………………………………………(1分)
答:台风中心从生成点(A点)到达B岛的速度是每小时25千米.…(1分)
(2)过点S作SH⊥ZD,垂足为点H,∴∠SHZ= 90°,
∵∠NZD=30°,∠CZN=7°,
∴∠CZD=∠CZN+∠NZD=7° + 30°=37°.………………………………(1分)
在Rt△SHZ中,sin∠CZD =.∵∠CZD=37°,SZ=250千米,
∴SH=SZ·sin∠CZD=(千米).………(2分)
∵150千米<170千米,
∴设台风中心移动到E处时上海开始遭受台风影响
到F处影响结束.即SE=SF=170(千米).
∵在Rt△SEH中,∠SHE= 90°,,
∴.(2分)
∴EF=2EH≈160(千米).……………(1分)
∴上海遭受这次台风影响的时间为
(小时).…………(1分)
答:上海遭受这次台风影响的时间为8小时.
23.证明:(1)∵,∴.………………………………(1分)
∵BD是AC边上的高,
∴∠BDC = 90°,△ADB和△ODC是直角三角形.…………………(1分)
∴Rt△ADB∽Rt△ODC.………………………………………………(1分)
∴∠ABD =∠OCD.……………………………………………………(1分)
又∵∠EOB=∠DOC,∠DOC+∠OCD+∠ODC=180°,
∠EOB +∠ABD+∠OEB =180°.
∴∠OEB = 90°.…………………………………………………………(1分)
∴CE⊥AB.………………………………………………………………(1分)
(2)在△ADB和△AEC中,
∵∠BAD=∠CAE,∠ABD =∠OCD,
∴△ADB∽△AEC.………………………………………………………(2分)
∴, 即.…………………………………………(1分)
在△DAE和△BAC中
∵∠DAE =∠BAC,.
∴△DAE∽△BAC.………………………………………………………(2分)
∵AF是∠BAC的平分线,
∴, 即.…………………………………(1分)
24.解:(1)设抛物线的表达式为.
由题意得:………………………………………………(1分)
解得:,.……………………………………………………(2分)
∴这条抛物线的表达式为.……………………………(1分)
注:用对称性求解析式酌情给分.
(2)令y = 0,那么,
解得,.………………………………………………………(1分)
∵点A的坐标是(3,0)∴点B的坐标是(1,0).…………………(1分)
∵C(0,2)∴,.…………………………………………(1分)
在Rt△ OBC中,∠BOC=90?,
∴.………………………………………………………(1分)
(3)设点E的坐标是(x,0),得OE=.
∵, ∴.
在Rt△ EOC中,∴.
∴=4,∴点E坐标是(4,0)或 (4,0).………………………(1分)
∵点C坐标是(0,2),
∴.……………………………………………(1分)
∴ ,或
解得和(舍去),或和(舍去);
∴点P坐标是(,)或(,).………………………(2分)
25.(1)证明:∵点G是Rt△ABC的重心,
∴CF是Rt△ABC的中线.…………………………………………(1分)
又∵在Rt△ABC,AC=BC,∠ACB=90°,
∴CF⊥AB,即∠AFC=90°.…………………………………………(1分)
∵∠DEF=∠ADE+∠DAE=∠EFC+∠ECF,且∠ADE=∠EFC=90°,
∴∠DAB=∠DCF.…………………………………………………(2分)
(2)解: 如右图,过点B作BH⊥CD于点H.
可证△CAD≌△BCH. ………………………(1分)
∴BH = CD = 2,CH = AD = x,DH = 2-x.(1分)
可证AD∥BH.∴.………………(1分)
,,.……………(1分)
.…………(1+1分)
(3)解: 当GC=GD时,如图1,
取AC的中点M,联结MD.那么MD=MC,
联结MG,MG⊥CD,且直线MG经过点B.那么BH与MG共线.
又CH=AD,那么AD=CH=.………………………………(2分)
当CG=CD时,如图2,即CG=2,点G为△ABC的重心,
,AB=2CF=6,,
.…………………………………(2分)
综上所述,AD=1或.
第 4 页 共 4 页
数 学 试 卷
(考试时间100分钟,满分150分)
考生注意:
1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.
2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.
3.本次测试可使用科学计算器.
一、选择题:(本大题共6题,每题4分,满分24分)
【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确选项的代号并填涂在答题纸的相应位置上】
1.如果把Rt△ABC的各边长都扩大到原来的n倍,那么锐角A的四个三角比值
(A)都缩小到原来的n倍; (B)都扩大到原来的n倍;
(C)都没有变化; (D)不同三角比的变化不一致.
2.已知P是线段AB的黄金分割点,且AP > BP,那么下列比例式能成立的是
(A); (B); (C); (D).
3.k为任意实数,抛物线的顶点总在
(A)直线上; (B)直线上; (C)x轴上; (D)y轴上.
4.如图在正三角形ABC中,点D、E分别在AC、AB上,且,AE = BE,那么有
(A)△AED∽△BED; (B)△BAD∽△BCD;
(C)△AED∽△ABD; (D)△AED∽△CBD.
5.下列命题是真命题的是
(A)经过平面内任意三点可作一个圆;
(B)相等的圆心角所对的弧一定相等;
(C)相交两圆的公共弦一定垂直于两圆的连心线;
(D)内切两圆的圆心距等于两圆的半径的和.
6.二次函数的图像如图所示,现有以下结论:
①;②;③;④;
其中正确的结论有
(A)1个; (B)2个;
(C)3个; (D)4个.
二、填空题:(本大题共12题,每题4分,满分48分)
【请将结果直接填入答题纸的相应位置上】
7.已知线段a = 4厘米,c = 9厘米,那么线段a和c的比例中项 ▲ 厘米.
8.在Rt△ABC中,∠C=90?,AB=10,,那么BC = ▲ .
9.抛物线在对称轴右侧的部分是 ▲ 的.(填“上升”或“下降”)
10.如果两个相似三角形的相似比为2︰3,两个三角形的周长的和是100cm,那么较小的三角形的周长为 ▲ cm.
11.为单位向量,与的方向相反,且长度为6,那么= ▲ .
12.某人从地面沿坡度的山坡走了100米,这时他离地面的高度是 ▲ 米.
13.已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在BC的延长线上的点E处,那么= ▲ .
14.已知在Rt△ABC中,∠C=90?,AC=3,BC=4,⊙C与斜边AB相切,那么⊙C的半径为 ▲ .
15.设抛物线l:的顶点为D,与y轴的交点是C,我们称以C为顶点,且过点D的抛物线为抛物线l的“伴随抛物线”,请写出抛物线的伴随抛物线的解析式 ▲ .
16.半径分别为3cm与cm的⊙O1与⊙O2相交于A、B两点,如果公共弦AB=cm,那么圆心距O1O2的长为 ▲ cm.
17.正五边形的边长与边心距的比值为 ▲ .(用含三角比的代数式表示)
18.如图,在等腰△ABC中,AB = AC = 4,BC = 6,点D在底边BC上,且∠DAC =∠ACD,将△ACD沿着AD所在直线翻折,使得点C落到点E处,联结BE,那么BE的长为 ▲ .
三、解答题:(本大题共7题,满分78分)
19.(本题满分10分)
已知二次函数图像的最高点是A(1,4),且经过点B(0,3),与轴交于C、D两点(点C在点D的左侧).求△BCD的面积.
20.(本题共2小题,第(1)小题2分,第(2)小题8分,满分10分)
已知:在平行四边形ABCD中,AB︰BC = 3︰2.
(1)根据条件画图:作∠BCD的平分线,交边AB于点E,
取线段BE的中点F,联结DF交CE于点G.
(2)设=,=,那么向量= ▲ ;
(用向量、表示),并在图中画出向量
在向量和方向上的分向量.
21.(本题共2小题,第(1)小题6分,第(2)小题4分,满分10分)
如图,梯形ABCD中,AD∥BC,∠ADC=90?,AD= 2,BC= 4,.以AB为直径作⊙O,交边DC于E、F两点.
(1)求证:DE=CF;
(2)求:直径AB的长.
22.(本题共2小题,第(1)小题3分,第(2)小题7分,满分10分)
2019年第18号台风“米娜”于9月29日早晨5点整,由位于台湾省周边的B岛东南方约980千米的西北太平洋洋面上(A点)生成,向西北方向移动.并于9月30日20时30分到达B岛后风力增强且转向,一路向北于24小时后在浙江省舟山市登陆.
“米娜”在登录后风力减弱且再一次转向,以每小时20千米的速度向北偏东30?的方向移动,距台风中心170千米的范围内是受台风影响的区域.已知上海位于舟山市北偏西7?方向,且距舟山市250千米.
(1)台风中心从生成点(A点)到达B岛的速度是每小时多少千米?
(2)10月2日上海受到“米娜”影响,那么上海遭受这次台风影响的时间有多长?
(结果保留整数,参考数据:,,;
,,.)
23.(本题共2小题,每小题6分,满分12分)
如图,在△ABC中,BD是AC边上的高,点E在边AB上,联结CE交BD于点O,且,AF是∠BAC的平分线,交BC于点F,交DE于点G.
求证:(1)CE⊥AB;
(2).
24.(本题共3题,每小题4分,满分12分)
已知:在平面直角坐标系xOy中,对称轴为直线x = -2的抛物线经过点C(0,2),与x轴交于A(-3,0)、B两点(点A在点B的左侧).
(1)求这条抛物线的表达式;
(2)联结BC,求∠BCO的余切值;
(3)如果过点C的直线,交x轴于点E,交抛物线于
点P,且∠CEO =∠BCO,求点P的坐标.
25.(本题共3小题,第(1)小题4分,第(2)小题6分,第(3)小题4分,满分14分)
已知:如图,在Rt△ABC和Rt△ACD中,AC=BC,∠ACB=90°,∠ADC=90°,CD=2,(点A、B分别在直线CD的左右两侧),射线CD交边AB于点E,点G是Rt△ABC的重心,射线CG交边AB于点F,AD=x,CE=y.
(1)求证:∠DAB=∠DCF;
(2)当点E在边CD上时,求y关于x的函数关系式,并写出x的取值范围;
(3)如果△CDG是以CG为腰的等腰三角形,试求AD的长.
闵行区2019学年第一学期九年级质量监控试卷
答案要点及评分标准
一、选择题:
1.C; 2.A; 3.B; 4.D; 5.C; 6.B.
二、填空题:
7.6; 8.4; 9.下降; 10.40; 11.-6; 12.50; 13.;
14.; 15.; 16.2或4; 17.().; 18.1.
三、解答题:
19.解:设所求的二次函数解析式为,………………………(2分)
把B(0,3)代入得解得:.…………………………(2分)
令,那么,解得:.………………………(2分)
∴CD=4.…………………………………………………………………………(2分)
在△BCD中,·CD·OB=.………………………………(2分)
20.解:(1)角平分线………………………………(1分)
整体画对;……………………………(1分)
(2)=.…………………(4分)
画图及结论正确.……………………(4分)
21.解:(1)过点O作OH⊥DC,垂足为H.
∵AD∥BC,∠ADC=90?,OH⊥DC,
∴∠BCN=∠OHC=∠ADC =90?.……(1分)
∴AD∥OH∥BC.……………………(1分)
又∵OA=OB.……………………………(1分)
∴DH=HC.……………………………(1分)
∵OH⊥DC,OH过圆心,
∴EH = HF.……………………………(1分)
∴DH-EH =HC-HF.………………(1分)
即:DE=CF.
(2)过点A作AG⊥BC,垂足为点G,∠AGB = 90°,
∵∠AGB =∠BCN = 90°,∴AG∥DC.
∵AD∥BC,∴AD=CG.……………………………………………………(1分)
∵AD= 2,BC= 4,∴BG= BC-CG =2.………………………………(1分)
在Rt△AGB中,∵,
∴.……………………………………………(1分)
在Rt△AGB中,
∴AB=.………………………………………………………………(1分)
22.解:(1)由题意得,AB=980千米,台风中心到达B岛的时间是39.5小时.…(1分)
∴(千米).…………………………………………………(1分)
答:台风中心从生成点(A点)到达B岛的速度是每小时25千米.…(1分)
(2)过点S作SH⊥ZD,垂足为点H,∴∠SHZ= 90°,
∵∠NZD=30°,∠CZN=7°,
∴∠CZD=∠CZN+∠NZD=7° + 30°=37°.………………………………(1分)
在Rt△SHZ中,sin∠CZD =.∵∠CZD=37°,SZ=250千米,
∴SH=SZ·sin∠CZD=(千米).………(2分)
∵150千米<170千米,
∴设台风中心移动到E处时上海开始遭受台风影响
到F处影响结束.即SE=SF=170(千米).
∵在Rt△SEH中,∠SHE= 90°,,
∴.(2分)
∴EF=2EH≈160(千米).……………(1分)
∴上海遭受这次台风影响的时间为
(小时).…………(1分)
答:上海遭受这次台风影响的时间为8小时.
23.证明:(1)∵,∴.………………………………(1分)
∵BD是AC边上的高,
∴∠BDC = 90°,△ADB和△ODC是直角三角形.…………………(1分)
∴Rt△ADB∽Rt△ODC.………………………………………………(1分)
∴∠ABD =∠OCD.……………………………………………………(1分)
又∵∠EOB=∠DOC,∠DOC+∠OCD+∠ODC=180°,
∠EOB +∠ABD+∠OEB =180°.
∴∠OEB = 90°.…………………………………………………………(1分)
∴CE⊥AB.………………………………………………………………(1分)
(2)在△ADB和△AEC中,
∵∠BAD=∠CAE,∠ABD =∠OCD,
∴△ADB∽△AEC.………………………………………………………(2分)
∴, 即.…………………………………………(1分)
在△DAE和△BAC中
∵∠DAE =∠BAC,.
∴△DAE∽△BAC.………………………………………………………(2分)
∵AF是∠BAC的平分线,
∴, 即.…………………………………(1分)
24.解:(1)设抛物线的表达式为.
由题意得:………………………………………………(1分)
解得:,.……………………………………………………(2分)
∴这条抛物线的表达式为.……………………………(1分)
注:用对称性求解析式酌情给分.
(2)令y = 0,那么,
解得,.………………………………………………………(1分)
∵点A的坐标是(3,0)∴点B的坐标是(1,0).…………………(1分)
∵C(0,2)∴,.…………………………………………(1分)
在Rt△ OBC中,∠BOC=90?,
∴.………………………………………………………(1分)
(3)设点E的坐标是(x,0),得OE=.
∵, ∴.
在Rt△ EOC中,∴.
∴=4,∴点E坐标是(4,0)或 (4,0).………………………(1分)
∵点C坐标是(0,2),
∴.……………………………………………(1分)
∴ ,或
解得和(舍去),或和(舍去);
∴点P坐标是(,)或(,).………………………(2分)
25.(1)证明:∵点G是Rt△ABC的重心,
∴CF是Rt△ABC的中线.…………………………………………(1分)
又∵在Rt△ABC,AC=BC,∠ACB=90°,
∴CF⊥AB,即∠AFC=90°.…………………………………………(1分)
∵∠DEF=∠ADE+∠DAE=∠EFC+∠ECF,且∠ADE=∠EFC=90°,
∴∠DAB=∠DCF.…………………………………………………(2分)
(2)解: 如右图,过点B作BH⊥CD于点H.
可证△CAD≌△BCH. ………………………(1分)
∴BH = CD = 2,CH = AD = x,DH = 2-x.(1分)
可证AD∥BH.∴.………………(1分)
,,.……………(1分)
.…………(1+1分)
(3)解: 当GC=GD时,如图1,
取AC的中点M,联结MD.那么MD=MC,
联结MG,MG⊥CD,且直线MG经过点B.那么BH与MG共线.
又CH=AD,那么AD=CH=.………………………………(2分)
当CG=CD时,如图2,即CG=2,点G为△ABC的重心,
,AB=2CF=6,,
.…………………………………(2分)
综上所述,AD=1或.
第 4 页 共 4 页
同课章节目录
