2020版高中数学新人教A版 必修3 第一章 算法初步阶段质量检测(一)(word版)
文档属性
| 名称 | 2020版高中数学新人教A版 必修3 第一章 算法初步阶段质量检测(一)(word版) |

|
|
| 格式 | zip | ||
| 文件大小 | 1010.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-18 00:00:00 | ||
图片预览


文档简介
阶段质量检测(一)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列计算S的值的选项中,不能设计算法求解的是( )
A.S=1+2+3+…+90
B.S=1+2+3+4
C.S=1+2+3+…+n(n≥2且n∈N)
D.S=15+25+35+…+2 015
2.下列赋值语句正确的是( )
A.a+b=5 B.5=a
C.a=2b=2 D.a=a+1
3.如图所示是一个循环结构的算法,下列说法不正确的是( )
A.①是循环变量初始化,循环就要开始
B.②是循环体
C.③是判断是否继续循环的终止条件
D.①可以省略不写
4.给出如图所示的程序框图,若输出的结果为2,则①处的执行框内应填的是( )
A.x=2 B.b=2
C.x=1 D.a=5
5.用秦九韶算法求当x=4时,多项式f(x)=7x6+6x5+3x2+2的值,先算的是( )
A.4×4=16 B.7×4=28
C.4×4×4=64 D.7×4+6=34
6.二进制数算式1 010(2)+10(2)的值是( )
A.1 011(2) B.1 100(2)
C.1 101(2) D.1 000(2)
7.当输入x=-1,y=20时,下列程序运行后输出的结果为( )
A.3,43 B.43,3
C.-18,16 D.16,-18
8.执行如图所示的程序框图,若输出的b的值为16,则图中判断框内①处应填( )
A.3 B.4
C.5 D.12
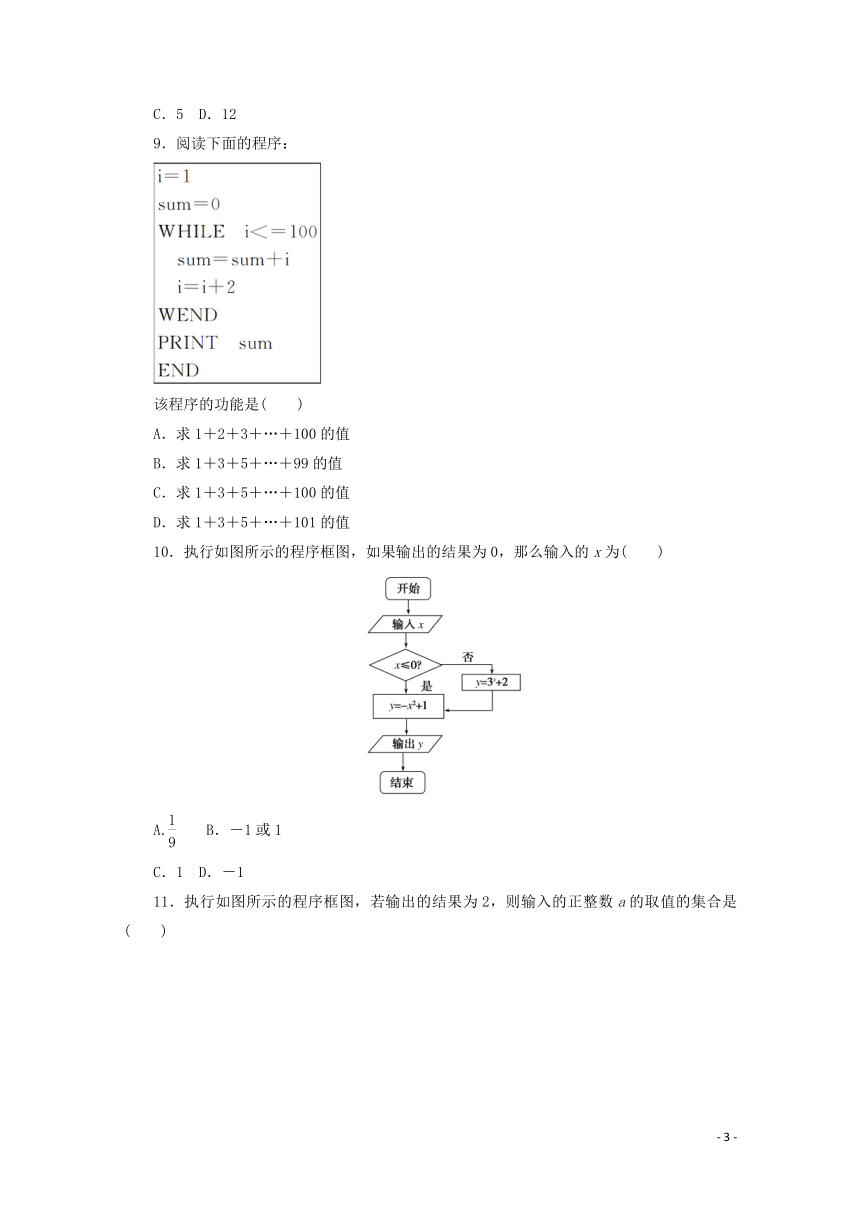
9.阅读下面的程序:
该程序的功能是( )
A.求1+2+3+…+100的值
B.求1+3+5+…+99的值
C.求1+3+5+…+100的值
D.求1+3+5+…+101的值
10.执行如图所示的程序框图,如果输出的结果为0,那么输入的x为( )
A. B.-1或1
C.1 D.-1
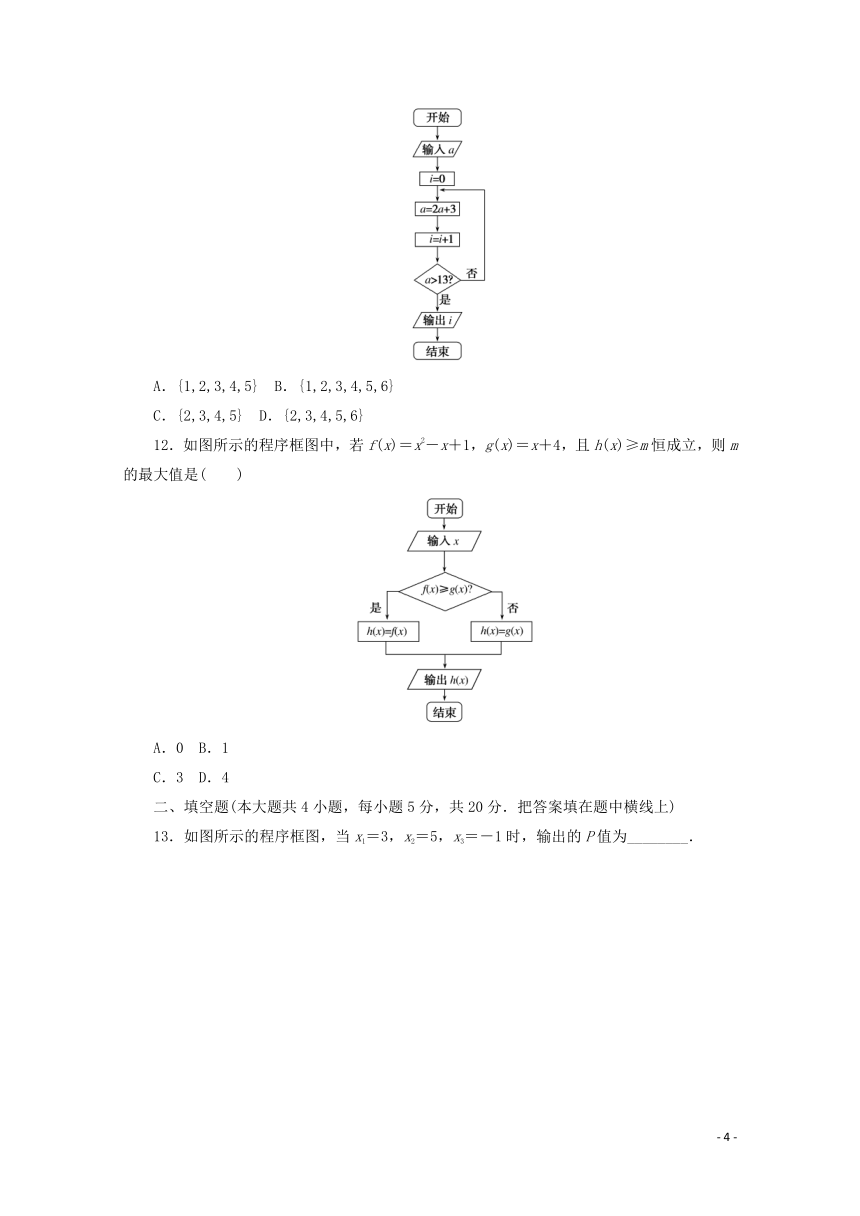
11.执行如图所示的程序框图,若输出的结果为2,则输入的正整数a的取值的集合是( )
A.{1,2,3,4,5} B.{1,2,3,4,5,6}
C.{2,3,4,5} D.{2,3,4,5,6}
12.如图所示的程序框图中,若f(x)=x2-x+1,g(x)=x+4,且h(x)≥m恒成立,则m的最大值是( )
A.0 B.1
C.3 D.4
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
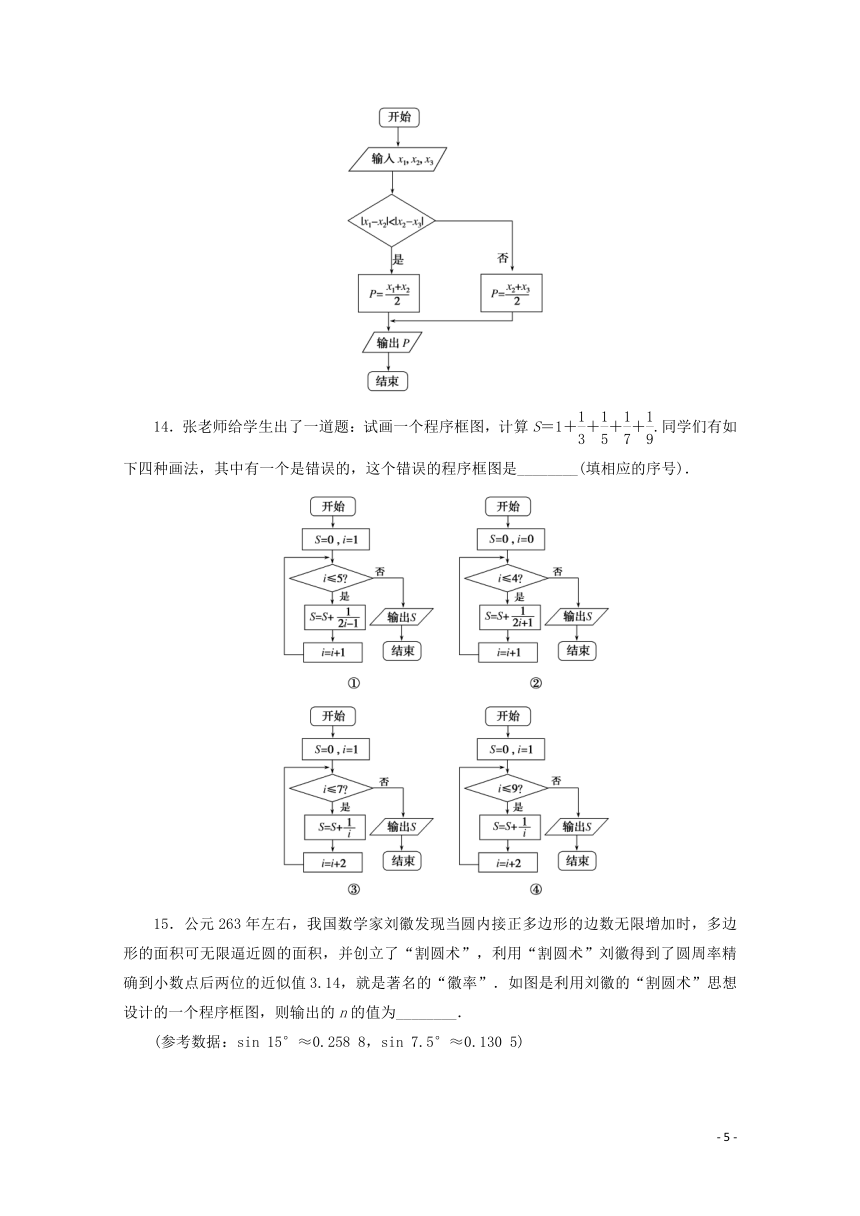
13.如图所示的程序框图,当x1=3,x2=5,x3=-1时,输出的P值为________.
14.张老师给学生出了一道题:试画一个程序框图,计算S=1++++.同学们有如下四种画法,其中有一个是错误的,这个错误的程序框图是________(填相应的序号).
15.公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的n的值为________.
(参考数据:sin 15°≈0.258 8,sin 7.5°≈0.130 5)
16.设2 134与1 455的最大公约数为m,则m化为三进制数为________.
三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明,证明过程或演算步骤)
17.(10分)下面给出了一个问题的算法:
第一步,输入x.
第二步,若x≥4,则y=2x-1;否则,y=x2-2x+3.
第三步,输出y.
问题:(1)这个算法解决的问题是什么?
(2)当输入的x值为多少时,输出的y值最小?
18.(12分)如图所示的程序框图的作用是输入x的值,输出相应的y的值.
(1)请指出该程序框图所使用的逻辑结构;
(2)若视x为自变量,y为函数值,试写出函数y=f(x)的解析式;
(3)若要使输入的x的值与输出的y的值相等,求输入的x的取值集合.
19.(12分)如图是将二进制数11 111(2)化为十进制数的一个程序框图.求框内应填入的条件.
20.(12分)某校50人参加数学竞赛,请设计一个程序框图,统计出这次竞赛成绩在80分以上的人数.
21.(12分)已知某算法的程序框图如图所示,若将输出的(x,y)值依次记为(x1,y1),(x2,y2),…,(xn,yn)……
(1)若程序运行中输出的一个数组是(9,t),求t的值;
(2)程序结束时,共输出(x,y)的组数为多少?
(3)写出程序框图的程序语句.
22.(12分)我国古代数学家张丘建编的《算经》中记有一道有趣的数学问题:“今有鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一.凡百钱,买鸡百只,问鸡翁、鸡母、鸡雏各几何?”你能用程序解决这个问题吗?
阶段质量检测(一)(解析版)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列计算S的值的选项中,不能设计算法求解的是( )
A.S=1+2+3+…+90
B.S=1+2+3+4
C.S=1+2+3+…+n(n≥2且n∈N)
D.S=15+25+35+…+2 015
解析:算法可以理解为按照要求设计好的、有限的、确切的计算序列,并且这样的步骤和序列可以解决一类问题.它的一个特点为有穷性,是指算法必须能在执行有限个步骤之后终止,而C项中S=1+2+3+…+n(n≥2且n∈N)中n是不确定的,所以不能设计算法求解.故选C.
答案:C
2.下列赋值语句正确的是( )
A.a+b=5 B.5=a
C.a=2b=2 D.a=a+1
解析:赋值语句的一般格式是变量=表达式,赋值号左右两边不能互换,赋值号左边只能是变量,而不能是表达式.
答案:D
3.如图所示是一个循环结构的算法,下列说法不正确的是( )
A.①是循环变量初始化,循环就要开始
B.②是循环体
C.③是判断是否继续循环的终止条件
D.①可以省略不写
解析:由程序框图可得,①为初始条件,不可省略,故D说法错误,故选D.
答案:D
4.给出如图所示的程序框图,若输出的结果为2,则①处的执行框内应填的是( )
A.x=2 B.b=2
C.x=1 D.a=5
解析:因为输出的结果是b=2,所以2=a-3,所以a=5,由2x+3=5,得x=1,故选C.
答案:C
5.用秦九韶算法求当x=4时,多项式f(x)=7x6+6x5+3x2+2的值,先算的是( )
A.4×4=16 B.7×4=28
C.4×4×4=64 D.7×4+6=34
解析:因为f(x)=anxn+an-1xn-1+…+a1x+a0=(…((anx+an-1)x+an-2)x+…+a1)x+a0,所以用秦九韶算法求当x=4时,多项式f(x)=7x6+6x5+3x2+2的值,先算的是7×4+6=34,故选D.
答案:D
6.二进制数算式1 010(2)+10(2)的值是( )
A.1 011(2) B.1 100(2)
C.1 101(2) D.1 000(2)
解析:二进制数的加法是逢二进一,所以选B.
答案:B
7.当输入x=-1,y=20时,下列程序运行后输出的结果为( )
A.3,43 B.43,3
C.-18,16 D.16,-18
解析:x=-1<0,y=20,所以经条件语句后x=23,y=20,则x-y=3,x+y=43,故选A.
答案:A
8.执行如图所示的程序框图,若输出的b的值为16,则图中判断框内①处应填( )
A.3 B.4
C.5 D.12
解析:按照程序框图依次执行:初始a=1,b=1;第一次循环后,b=21=2,a=1+1=2;第二次循环后,b=22=4,a=2+1=3;第三次循环后,b=24=16,a=3+1=4,而此时应输出b的值.故判断框中的条件应为“a≤3?”.故选A.
答案:A
9.阅读下面的程序:
该程序的功能是( )
A.求1+2+3+…+100的值
B.求1+3+5+…+99的值
C.求1+3+5+…+100的值
D.求1+3+5+…+101的值
解析:由“i=i+2”可知,该程序中循环变量每次的增量是2,且当i=99时,i≤100,继续执行循环体“sum=sum+99,i=i+2”,当i=101时,101>100,循环终止,输出sum的值,此时sum=1+3+5+…+99.
答案:B
10.执行如图所示的程序框图,如果输出的结果为0,那么输入的x为( )
A. B.-1或1
C.1 D.-1
解析:当x≤0时,由-x2+1=0,得x=-1;当x>0时,第一次对y赋值为3x+2,第二次对y又赋值为-x2+1,最后y=-x2+1,于是由-x2+1=0,得x=1,综上知输入的x值为-1或1,故选B.
答案:B
11.执行如图所示的程序框图,若输出的结果为2,则输入的正整数a的取值的集合是( )
A.{1,2,3,4,5} B.{1,2,3,4,5,6}
C.{2,3,4,5} D.{2,3,4,5,6}
解析:若输入a=1,则a=2×1+3=5,i=0+1=1,因为5>13不成立,所以继续循环;a=2×5+3=13,i=1+1=2,因为13>13不成立,所以继续循环;a=2×13+3=29,i=2+1=3,因为29>13成立,所以结束循环,输出的结果为3,不为2,所以a≠1,排除A,B.若输入a=6,则a=2×6+3=15,i=0+1=1,因为15>13成立,所以输出的结果为1,不为2,所以a≠6,排除D,故选C.
答案:C
12.如图所示的程序框图中,若f(x)=x2-x+1,g(x)=x+4,且h(x)≥m恒成立,则m的最大值是( )
A.0 B.1
C.3 D.4
解析:由程序框图知,
h(x)=
即h(x)=
数形结合求得h(x)min=h(-1)=3,
因为h(x)≥m恒成立,
所以m≤h(x)min=3.
答案:C
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.如图所示的程序框图,当x1=3,x2=5,x3=-1时,输出的P值为________.
解析:依题意得,当x1=3,x2=5,x3=-1时,
|x1-x2|<|x2-x3|,P==4,
因此输出P值是4.
答案:4
14.张老师给学生出了一道题:试画一个程序框图,计算S=1++++.同学们有如下四种画法,其中有一个是错误的,这个错误的程序框图是________(填相应的序号).
解析:③中,当i=7时,执行最后一次循环,此时S=S+,与题意不符合.
答案:③
15.公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的n的值为________.
(参考数据:sin 15°≈0.258 8,sin 7.5°≈0.130 5)
解析:第1次执行循环体后,S=×6×sin 60°=,不满足退出循环的条件,则n=12;第2次执行循环体后,S=×12×sin 30°=3,不满足退出循环的条件,则n=24;第3次执行循环体后,S=×24×sin 15°≈3.105 6,满足退出循环的条件,故输出的n的值为24.
答案:24
16.设2 134与1 455的最大公约数为m,则m化为三进制数为________.
解析:2 134=1 455×1+679,1 455=679×2+97,679=97×7,所以2 134与1 455的最大公约数为97,即m=97,用除3取余法可得,97化为三进制数为10 121(3).
答案:10 121(3)
三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明,证明过程或演算步骤)
17.(10分)下面给出了一个问题的算法:
第一步,输入x.
第二步,若x≥4,则y=2x-1;否则,y=x2-2x+3.
第三步,输出y.
问题:(1)这个算法解决的问题是什么?
(2)当输入的x值为多少时,输出的y值最小?
解析:(1)这个算法解决的问题是求分段函数y=的函数值.
(2)当x≥4时,y=2x-1≥7;当x<4时,y=x2-2x+3=(x-1)2+2≥2,所以ymin=2,此时x=1.即当输入的x值为1时,输出的y值最小.
18.(12分)如图所示的程序框图的作用是输入x的值,输出相应的y的值.
(1)请指出该程序框图所使用的逻辑结构;
(2)若视x为自变量,y为函数值,试写出函数y=f(x)的解析式;
(3)若要使输入的x的值与输出的y的值相等,求输入的x的取值集合.
解析:(1)条件结构和顺序结构.
(2)解析式为y=.
(3)依题意,得或或,
解得x=0或1或3.
故所求的集合为{0,1,3}.
19.(12分)如图是将二进制数11 111(2)化为十进制数的一个程序框图.求框内应填入的条件.
解析:由二进制数转换为十进制数的方法可知11 111(2)=1+2×1+1×22+1×23+1×24,框图中i是计数变量,i=1时,S=1+2×1;i=2时,S=1+1×2+1×22;i=3时,S=1+1×2+1×22+1×23;i=4时,S=1+1×2+1×22+1×23+1×24,此时i=5,停止循环,所以条件应填i>4.
20.(12分)某校50人参加数学竞赛,请设计一个程序框图,统计出这次竞赛成绩在80分以上的人数.
解析:算法分析:用循环结构,将50个分数逐个输入,用条件结构,将高于80分的选出;再设计一个计数变量,将80分以上的人数逐个相加.
程序框图如下:
21.(12分)已知某算法的程序框图如图所示,若将输出的(x,y)值依次记为(x1,y1),(x2,y2),…,(xn,yn)……
(1)若程序运行中输出的一个数组是(9,t),求t的值;
(2)程序结束时,共输出(x,y)的组数为多少?
(3)写出程序框图的程序语句.
解析:(1)由程序框图知:当x=1时,y=0;当x=3时,y=-2;当x=9时,y=-4,所以t=-4.
(2)当n=1时,输出一对,当n=3时,又输出一对,…,当n=2 009时,输出最后一对,共输出(x,y)的组数为1 005;
(3)程序框图的程序语句如下图:
22.(12分)我国古代数学家张丘建编的《算经》中记有一道有趣的数学问题:“今有鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一.凡百钱,买鸡百只,问鸡翁、鸡母、鸡雏各几何?”你能用程序解决这个问题吗?
解析:设鸡翁、鸡母、鸡雏各x,y,z只,
则
由②,得z=100-x-y,③
③代入①,得5x+3y+=100,
即7x+4y=100.④
求方程④的解,可由程序解之.
PAGE
- 1 -
