华师大版数学七年级上册:第五章 相交线与平行线 学案(共6课时,无答案)
文档属性
| 名称 | 华师大版数学七年级上册:第五章 相交线与平行线 学案(共6课时,无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 345.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-26 00:00:00 | ||
图片预览


文档简介
《对顶角》导学案
班级: 组名: 组别: 姓名:
【学习目标】
1、认识对顶角。
2、理解对顶角相等这一性质。
3、能用“对顶角相等”这一性质解决一些简单的实际问题。
【重点难点】
重点:理解对顶角相等的性质并能运用
难点:对顶角的认识。
【学法指导】阅读教材160页——162页,
【知识链接】
补角和邻补角定义。
【学习过程】
知识点一:对顶角的概念
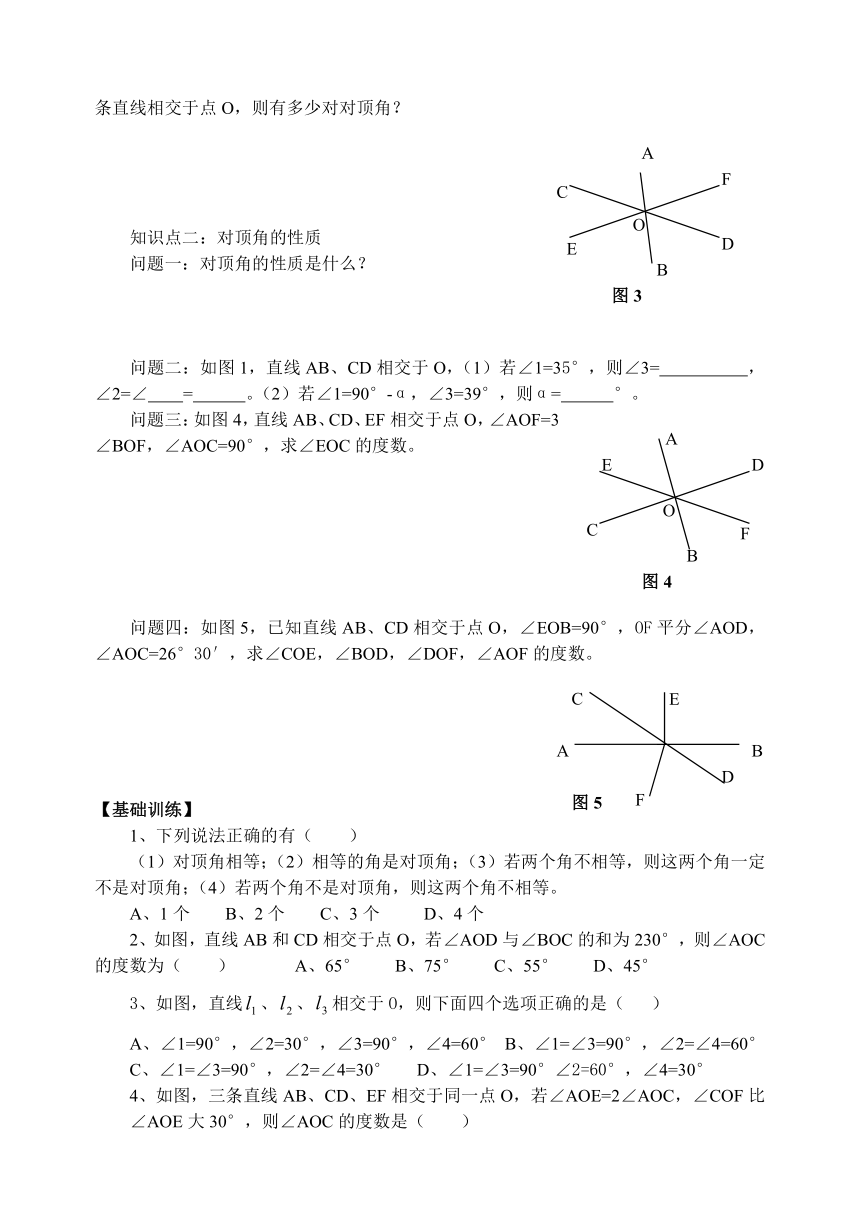
问题一:如图1,直线AB、CD相交于O,图中∠1和∠2的位置和数量关系分别是什么?如果还有存在这样关系的角,请找出来,并说明它们的位置关系和数量关系
问题二:如图1,直线AB、CD相交于O,图中∠1和∠3又有什么关系?如果还有存在这样关系的角,请找出来。
问题三:什么是对顶角?请找出图2中的对顶角。
问题四:如图3,直线AB、CD、EF相交于点O,图中共有几对对顶角?如果有条直线相交于点O,则有多少对对顶角?
知识点二:对顶角的性质
问题一:对顶角的性质是什么?
问题二:如图1,直线AB、CD相交于O,(1)若∠1=35°,则∠3= ,∠2=∠ = 。(2)若∠1=90°-α,∠3=39°,则α= °。
问题三:如图4,直线AB、CD、EF相交于点O,∠AOF=3∠BOF,∠AOC=90°,求∠EOC的度数。
问题四:如图5,已知直线AB、CD相交于点O,∠EOB=90°,OF平分∠AOD,∠AOC=26°30′,求∠COE,∠BOD,∠DOF,∠AOF的度数。
【基础训练】
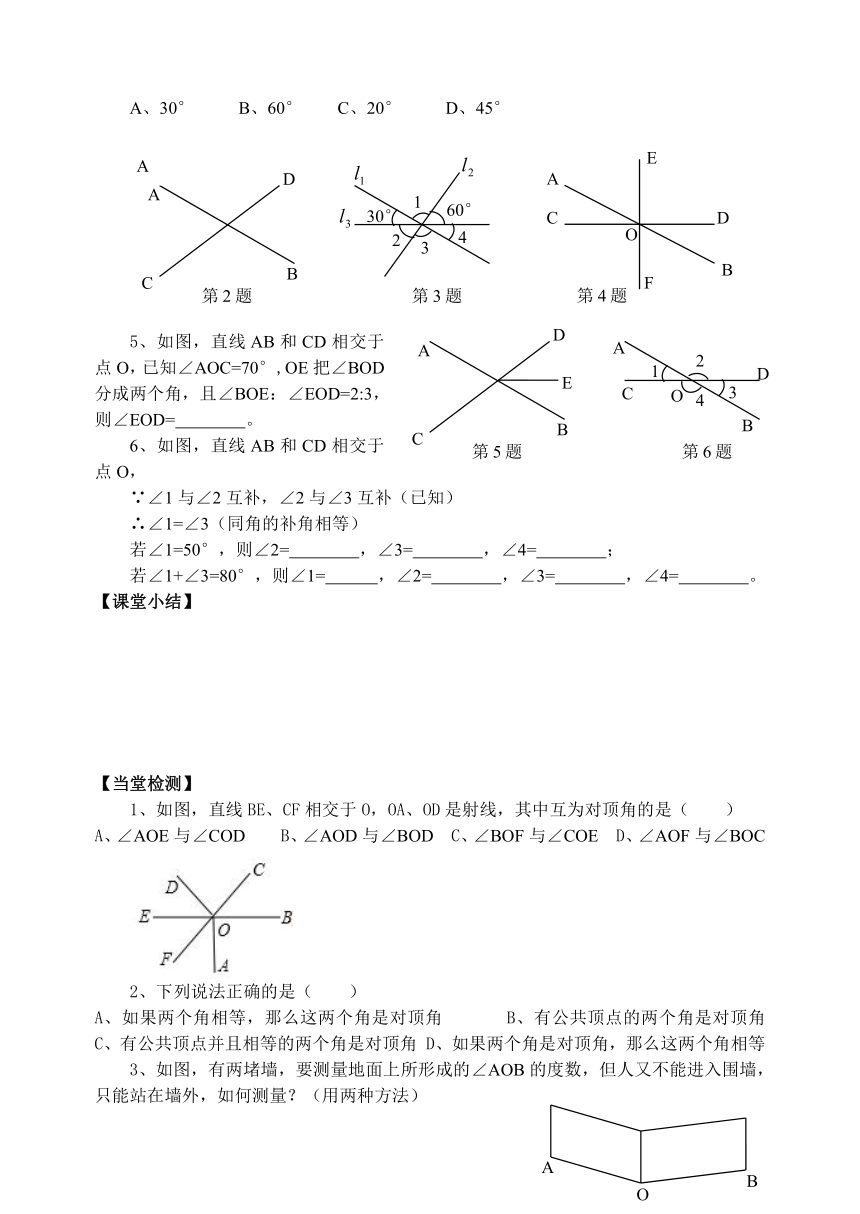
1、下列说法正确的有( )
(1)对顶角相等;(2)相等的角是对顶角;(3)若两个角不相等,则这两个角一定不是对顶角;(4)若两个角不是对顶角,则这两个角不相等。
A、1个 B、2个 C、3个 D、4个
2、如图,直线AB和CD相交于点O,若∠AOD与∠BOC的和为230°,则∠AOC的度数为( ) A、65° B、75° C、55° D、45°
3、如图,直线、、相交于O,则下面四个选项正确的是( )
A、∠1=90°,∠2=30°,∠3=90°,∠4=60° B、∠1=∠3=90°,∠2=∠4=60°C、∠1=∠3=90°,∠2=∠4=30° D、∠1=∠3=90°∠2=60°,∠4=30°
4、如图,三条直线AB、CD、EF相交于同一点O,若∠AOE=2∠AOC,∠COF比∠AOE大30°,则∠AOC的度数是( )
A、30° B、60° C、20° D、45°
5、如图,直线AB和CD相交于点O,已知∠AOC=70°,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3,则∠EOD= 。
6、如图,直线AB和CD相交于点O,
∵∠1与∠2互补,∠2与∠3互补(已知)
∴∠1=∠3(同角的补角相等)
若∠1=50°,则∠2= ,∠3= ,∠4= ;
若∠1+∠3=80°,则∠1= ,∠2= ,∠3= ,∠4= 。
【课堂小结】
【当堂检测】
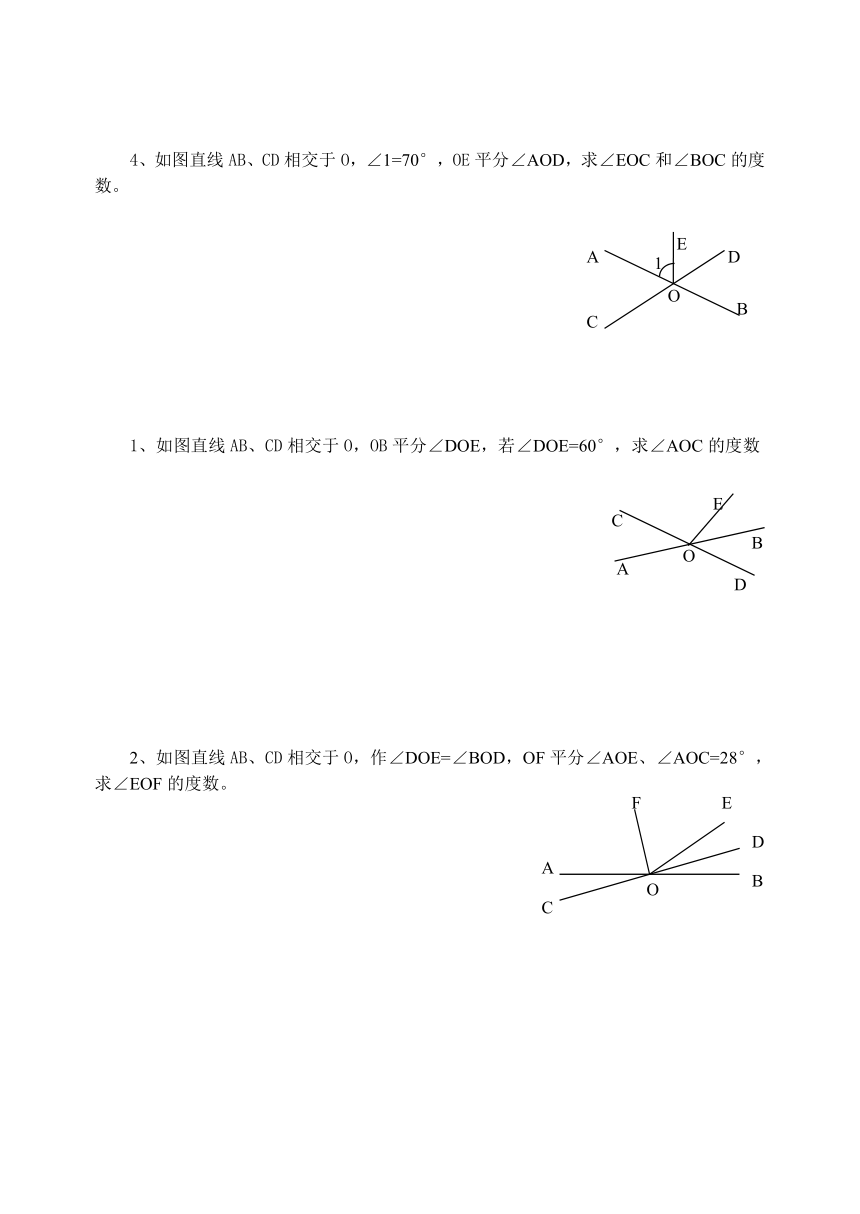
1、如图,直线BE、CF相交于O,OA、OD是射线,其中互为对顶角的是( )
A、∠AOE与∠COD B、∠AOD与∠BOD C、∠BOF与∠COE D、∠AOF与∠BOC
2、下列说法正确的是( )
A、如果两个角相等,那么这两个角是对顶角 B、有公共顶点的两个角是对顶角 C、有公共顶点并且相等的两个角是对顶角 D、如果两个角是对顶角,那么这两个角相等
3、如图,有两堵墙,要测量地面上所形成的∠AOB的度数,但人又不能进入围墙,只能站在墙外,如何测量?(用两种方法)
4、如图直线AB、CD相交于O,∠1=70°,OE平分∠AOD,求∠EOC和∠BOC的度数。
1、如图直线AB、CD相交于O,OB平分∠DOE,若∠DOE=60°,求∠AOC的度数
2、如图直线AB、CD相交于O,作∠DOE=∠BOD,OF平分∠AOE、∠AOC=28°,求∠EOF的度数。
《垂线》导学案
班级: 组名: 组别: 姓名:
【学习目标】
1、知道垂线、垂线段的定义和垂线的性质,体会点到直线的距离。
2、知道过一点有且只有一条直线垂直于已知直线,会用三角尺或量角器过一点画一条直线的垂线。
【重点难点】
垂线、垂线段、点到直线的距离的定义
【学法指导】阅读教材162页——165页,动手实验去检验教材中的结论
【知识链接】相交线及对顶角,跳远的测量方法
【学习过程】
知识点一:垂线
问题一:什么是垂直?请举例说明如何表示两条互相垂直的直线;什么是垂线?请画图说明;你能举例说出生活中垂线吗?
问题二:过一点如何画已知直线的垂线?有几种情况?请画图说明。
问题三:过一点画已知直线的垂线有几条?
问题四:如图,直线AB、CD相交于O,OE⊥CD,OF⊥AB,∠DOF=65°,求∠BOE和∠AOC的度数。
知识点二:垂线段
问题一:什么是垂线段?并画图说明。
问题二:什么是点到直线的距离?
问题三:如图,按要求画图:(1)点A到DC的距离AE;(2)连结AC,点B到AC的距离BF。
【基本训练】
1、下列说法正确的是( )
A、过一点有无数条直线与已知直线垂直 B、和一条直线垂直的直线有且只有一条C、过一点有且只有一条直线与已知直线垂直 D、两直线相交则必垂直
2、画一条线段的垂线,垂足在( )
A、线段上 B、线段的端点上 C、线段的延长线上 D、以上都有可能
3、如图,∠BAC=90°,AD⊥BC于D,则下面的结论正确的是( )
(1)线段AB是点B到AC的垂线段(2)线段AC是点C到AB的垂线段(3)线段AD是点D到BC的垂线段(4)线段BD是点B到AD的垂线段
A、1个 B、2个 C、3个 D、4个
4、如图直线AB、CD相交于O,OM⊥AB于O,且∠DOM=∠COM,求∠AOD的度数。
【当堂检测】
1、如果两条直线相交所成的四个角都是直角,那么两条直线互相 。
2、如图,OA⊥OC, ∠AOB: ∠AOC=2:3,∠BOC= 。
3、画线段AB的垂线有 条,过线段AB的中点P画线段AB的垂线有 条。
4、如图,已知三条直线AB、CD、EF相交于O,且EF⊥AB,(1)若
∠DOE=50°,则∠BOD= , ∠AOD= .(2)若∠COB=β,则∠BOD=
, ∠DOE= 。
5、如图,已知OA⊥m,OB⊥m,所以OA与OB重合,其理由是
( )A、过两点只有一条直线 B、过一点只能做一条垂线
C、经过一点只有一条直线垂直于已知直线 D、垂线段最短
【课堂小结】
现在你有哪些收获?
【拓展训练】
1、下列说法:(1)直线外一点与直线上各点的所有连线中,垂线段最短.(2)互为邻补角的两个角的平分线一定垂直。(3)两条直线相交,如果有两个角相等,那么这两条直线垂直。(4)两条直线相交,如果有3个角相等,那么这两条直线垂直。其中正确的有( )
A、1个 B、2个 C、3个 D、4个
2、直线m外一点P,它到直线m上点A、B、C的距离分别是6cm、3cm、5cm,则点P到直线的距离为( )
A、不大于3cm B、3cm C、5cm D、6cm
3、如图,三条直线相交于一点,若∠1: ∠2:∠3=1:2:3,求∠2.
《同位角、内错角、同旁内角》导学案
班级: 组名: 组别: 姓名:
【学习目标】
能根据图形判断哪些角是同位角、内错角、同旁内角。
【重点难点】
从不同图形重中找出不同位置关系的角
【知识链接】
对顶角及性质,邻补角
【学法指导】
阅读教材第166页——第168页,根据图形特点正确确定角的位置关系
【学习过程】
知识点一:同位角、内错角、同旁内角
问题一:什么同位角、内错角、同旁内角?
1、分别在两条直线的同侧,并且都在第三条直线的同旁,这样的两个角叫做 角,在两条直线之间,分别在第三条直线的两旁,这样的两个角叫做 角,在两条直线之间,并且在第三条直线的同旁,这样的两个角叫做 角。
2、如图,∠1与∠2是 角,∠1与∠3是 角,∠1与∠4是 角。
3、如图,∠5的同位角是 ,∠2的内错角是 ,∠3的同旁内角是 。
问题二:如图,∠1与∠B是 角,∠A与∠2是 角,∠ACD与 是内错角,∠BCD与∠B是 角,∠A与∠B是 角,∠ACE与∠3是 角。
问题三:如图,直线PQ与直线AB、射线MG交于点M,直线PQ与CD、EF交于点N,指出图中∠1与∠4,∠2与∠4,∠3与∠MNF是哪两条直线被哪一条直线截得的什么角?
【基本训练】
1、如图,同位角是( )
A、∠C和∠6,∠6和∠D B、∠2和∠3,∠1和∠D C、∠2和∠6,∠3和∠4 D、∠1和∠D,∠6和∠D
2、如图,图中与∠α是内错角关系的角有( )
A、1个 B、2个 C、3个 D、4个
3、如图,∠2的内错角是 ,∠3和∠B是 ,∠B的同旁内角是 。
4、如图,∠B与∠EAC是同位角,∠B与∠ACD是 ,∠EAC与∠ACD是同旁内角,∠BAC与∠ACD是 。
5、如图,直线AB、CD、EF两两相交,指出∠3与其他角(带数字标注)是什么关系的角?
【当堂检测】
1、如图,∠1和∠2是同位角的个数有( )
A、1个 B、2个 C、3个 D、4个
2、如图,下列说法错误的是( )
(1)∠1与∠3是同位角,(2)∠1与∠2是同位角,(3)∠1与∠2是同旁内角,(4)∠1与∠4是内错角
A、(1)和(2) B、(2)和(3) C、(2)和(4) D、(3)和(4)
3、如图,能与∠1构成同位角的角有( )
A、1个 B、2个 C、3个 D、4个
4、如图,与∠1成同位角的角有 个,与∠1成内错角的角有 个,与∠1成同旁内角的角有 个,
5、如图,∠1与∠2是直线 和直线 被第三条直线 所截而成的 角,∠2和∠3是直线 和直线 被第三条直线 所截而成的 角。
【课堂小结】
1、你有哪些收获?
2、还有什么疑惑?
【拓展训练】
1、如图,(1)∠1与∠3是直线 与直线 被直线 所截得到的
角。(2)∠2与∠3是直线 与直线 被直线 所截得到的 角。
2、如图,下列说法错误的是( )
A、∠1与∠2是内错角 B、∠2与∠4是对顶角
C、∠3与∠5是同旁内角 D、∠3与∠2是同位角
《平行线》导学案
班级: 组名: 组别: 姓名:
【学习目标】
1、知道平行线的定义,体会“平行公理”这个基本事实。
2、能画出已知直线的平行线。
【重点难点】
平行线的定义和平行公理
【学法指导】阅读教材169——170页,用动手操作试验的方法去学习。
【知识链接】
小学学过的平行知识以及生活中见过的平行
【学习过程】
知识点一:平行线
问题一:什么叫平行线?
问题二:下列说法中正确的是( ) A、不相交的两条直线时平行线 B、同一平面内,不相交的两条射线叫做平行线 C、在同一平面内,两条直线不相交就重合 D、同一平面内,没有公共点的两条直线时平行线
知识点二:平行公理
问题一:过直线外一点可以画多少条直线和这条直线平行?请动手画一画。
问题二:若两条直线都和第三条直线平行,则这两条直线有什么样的位置关系?
问题三:判断:
(1)不相交的两条直线是平行线 ( )
(2)过一点可以且只可以画一条直线与已知直线平行 ( )
(3)过相交直线AB、CD外一点E,作直线EF平行于AB且平行于CD( )
例3 已知:D是∠AOB内部一点,如图,过D作DE∥AO,作DF∥BO分别交OA、OB于F、E,画出图形,并说明四边形DEOF是什么图形?
【基本训练】
1、下列说法正确的是( )
A、在同一平面内,不重合的两条直线的位置关系只有相交、平行两种
B、在同一平面内,不相交的两条线段互相平行
C、不相交的两条直线是平行线
D、在同一平面内,不相交的两条射线互相平行
2、若a、b、c是三条直线,如果a∥b∥c,那么( )
A、a∥b B、a∥c C、a=c D、以上全不对
3、在同一平面内,两条直线的位置关系有 种,它们分别是 。
4、在同一平面内,与已知直线平行的直线有 条,过直线l外一点M与已知直线l平行的直线有 。
5、直线同侧有A、B、C三点,如果A、B两点确定的直线1与平行,B、C两点确定的直线????2也与平行,则A、B、C三点 其依据是 。
【课堂小结】
1、这节课有什么收获?
2、还有什么疑惑?
【当堂检测】
1、直线AB、CD、a、b在同一平面内,且AB∥CD,直线a与AB、CD都相交,直线b与AB、CD都相交,则直线a、b的位置关系是( )
A、相交 B、平行 C、垂直 D、相交或平行
2、若b∥c,a∥c,则 ∥ ,其理由是 。
3、如图在长方体中,互相平行的棱有 ,相交的棱有 ,既不平行也不相交的棱有 。(每空只需写出2组)。
4、在同一平面内,三条直线的交点最多是 个,最少是 个。
5、如图,AD∥BC,M是CD上的一点,在图中过点M画直线MN∥AD,则直线MN与BC的位置关系是 。
【拓展训练】
1、下列说法不正确的是( )A、过任意一点P可作已知直线L的一条平行线 B、同一平面内的两条不相交的直线是平行线 C、过直线外一点只能画一条直线与已知直线平行 D、平行于同一条直线的两条直线平行
2、如图,四边形ABCD和四边形AFCE都是平行四边形,点E、F分别在CD、AB上,则图中平行线的组数是( ) A、2 B、3 C、4 D、5
3、如图,(1)你能用学过的方法判断 a、b这两条直线的位置关系吗?
(2)过直线外一点A画直线c的平行线。(3)找出图中所有的平行线,并用“∥”表示。
《平行线的判定》导学案
班级: 组名: 组别: 姓名:
【学习目标】
1、知道平行线的三种判定方法,并能用这些方法判断两条直线是否平行。
2、学会一些简单的推理
【重点难点】
平行线的三种判定方法
【学法指导】阅读教材171——174页,通过动手试验去检验平行线的又一个基本事实
【知识链接】平行线和三线八角
【学习过程】
知识点一:平行线的判定方法
问题一:平行线的判定方法有哪些?
问题二:如图,(1)若∠1=∠2,则可以判定哪两条直线平行?说明理由
(2)若∠1=∠M,可判定哪两条直线平行?说明理由
(3)若∠C+∠A=180°,可判定哪两条直线平行?理由
问题三:如图,如果∠1=∠A,那么 ∥ ;若满足 ,则可得AD∥EF,(填一个即可)
问题四: 写出图中能使AB∥CD成立的各种条件。
【基本训练】
1、如图,如果∠1=∠2,那么根据 ,可得 ∥
;如果∠DAB+∠ABC=180°,那么根据 ,可得 ∥ ;如果∠3=∠B,那么根据 ,可得 ∥ 。
2、如图,∠1=70°,∠B=70°,∠C=130°,那么平行的直线是 。
3、如图,若使DE∥BC,则需要满足的条件是 (填一种)。
4、下列说法正确的个数是( ) (1)不相交的两条直线互相平行;(2)a∥b,b∥c,则a∥c;(3)在同一平面内,a⊥b,c⊥b,则a⊥c;(4)同旁内角相等,两直线平行。 A、1个 B、2个 C、3个 D、4个
【课堂小结】
你有什么收获?
你有什么新发现?
【当堂检测】
1、A、B是直线外不同的两点,直线a过点A,a⊥,直线b过点B,b⊥,则a、b的关系是( ) A、相交 B、平行 C、重合 D、平行或重合
2、如图,若∠1与∠2互补,∠2与∠4互补,则( )
A、3∥4 B、2∥5 C、1∥5 D、1∥3
3、两条直线被第三条直线所截,则( )
A、同位角必相等 B、内错角必相等 C、同旁内角必互补 D、以上结论均不对
4、如图,下列条件中不能判断直线1∥2的是( )
A、∠1=∠3 B、∠2=∠3 C、∠4=∠5 D、∠2+∠4=180°
5、如图,直线a、b被直线c所截,现在给出下列四个条件:(1)∠1=∠5;(2)∠1=∠3;(3)∠2+∠3=180°;(4)∠4=∠7,其中能判定a∥b的条件序号是( )
A、(1)(2) B、(1)(3) C、(1)(4) D、(3)(4)
6、如图(1)∵∠1= (已知),
∴DE∥ ;( )
(2)∵∠2= (已知)
∴EF∥ ;( )
(3)∵∠2= (已知)
∴BC∥ ;( )
(4)∵∠3+ =180°(已知)
∴BC∥ ;( )
【拓展训练】
1、如图,∠1=∠2,∠4=∠C,∠C+∠CDB=180°,求证:DE∥BF
2、如图,∠A=∠2, ∠E=∠1,AD⊥ED,那么AB∥CE吗?为什么?
《平行线的性质》导学案
班级: 组名: 组别: 姓名:
【学习目标】
1、知道平行线的三个性质。
2、能区别平行线的性质与平行线的识别,能用平行线的判定与性质解决问题。
3、体会推理过程,会用几何语言进行表达。
【重点难点】
1、平行线的性质
2、平行线的判定与性质的综合运用
【学法指导】
结合平行线的判定用类比的方法去阅读教材第175页——第178页,并用笔标注好重点难点的内容。
【知识链接】平行线的判定方法
【学习过程】
知识点一:平行线的性质
问题一:平行线的性质有哪些?
问题二:如图,l1∥l2,∠1=100°,那么∠2= .
问题三:如图,四边形ABCD为一个平行四边形,即AB∥CD,AD∥BC,则∠1与∠2的关系是 。
知识点二:平行线性质的运用
问题一: 如图AB∥DE,DF∥BC,∠1=62°,求∠2、∠3的度数。
问题二: 如图,已知直线a、b、c被直线d所截,若∠1=∠2,∠2+∠3=180°,
求证:∠1=∠7
【基本训练】
1、如图,(1)若AD∥BC,那么根据 ,可得∠1= ;(2)若AB∥CD,那么根据 ,可得∠1= 。
2、如图,AB∥CD, ∠1=40°,则∠2= 。
3、如图AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2= 。
4、如图,(1)若AD∥BC,那么根据两直线平行,同旁内角互补,可得∠ +
∠ABC=180°;(2)若AB∥CD,则由两直线平行,同旁内角互补,可得∠
+∠ABC=180°。
5、如图直线AB、CD被直线EF所截,若∠1=∠2,则∠AEF+∠CFE= 。
八、小结
你有哪些收获?
【当堂检测】
1、如图,AB∥CD,若∠2是∠1的2倍,则∠2等于( )
A、60° B、90 C、120° D、150°
2、已知:如图,直线∥,∠1=40°,那么∠2= 度。
3、如图,AB∥CD,AD∥BC,如果∠B=50°,那么∠D= 。
4、若点A在点B的北偏东40°方向,那么点B在点A的 方向。
5、如图,AD平分∠BAC,∠1=∠2,试说明∠1=∠M的理由。
【拓展练习】
1、如图,AB∥EF∥DC,EG∥DB,则图中与∠1相等的角(∠1除外)共有( )个
A、6 B、5 C、4 D、3
2、如图,若AB∥CD,则正确的是( )
A、∠1=∠2+∠3 B、∠1=∠2=∠3 C、∠1+∠2+∠3=180° D、∠1=∠2+∠3=180°
3、如图,a∥c,∠1=70°,∠2=110°,∠3=115°。求∠ 4的度数。
4、如图,若AC∥BD,∠1=∠4,则下列结论:(1)∠CAB=∠ABD,(2)AE∥BF,(3)∠2=∠3,(4)∠CAB=∠3+∠4,其中正确的有( )个。
A、1 B、2 C、3 D、4
5、如图,已知AD∥EF,若AD平分∠BAC,请说明∠1与∠2有何关系?
O
1
2
3
4
C
A
D
B
图1
F
E
D
C
B
A
H
G
图2
图3
D
C
F
E
B
O
A
A
图4
D
C
F
E
B
O
C
A
F
E
D
B
图5
A
D
C
B
A
2
O
E
4
3
1
C
D
B
A
第5题
第6题
第4题
O
A
E
F
B
D
C
60°
30°
4
3
2
1
C
C
C
C
D
B
A
第2题
第3题
B
A
O
C
1
O
D
E
A
B
B
E
C
O
D
A
A
C
O
D
E
F
B
C
O
F
D
B
E
A
A
B
C
D
A
B
D
C
A
C
M
B
D
2题图
C
O
B
A
C
A
E
D
B
F
O
4题图
B
A
O
m
3
2
1
P
4
1
M
3
2
N
3
2
1
B
A
D
E
C
C
E
Q
D
F
B
A
G
问题二图
问题三图
2
2
1
3
4
5
1
a
b
4
3
B
C
A
D
E
2题图
3题图
3
1
2
4题
3题
2题
1题
D
C
B
A
E
B
D
A
E
C
α
B
A
D
C
5
1
6
2
4
3
F
7
8
D
E
B
5
6
2
C
1
A
4
3
1
2
2
1
1
2
1
1
2
2
1
A
B
1
2
3
1
1
2
3
4
5
1
D
E
第2题
第3题
第4题
第5题
5
4
2
3
1
2
4
3
1
1题
2题
●D
O
A
B
A1
B1
C1
D1
A
C
D
B
A
B
C
D
M
●
3题
5题
a
b
B
F
C
A
E
D
A●
c
E
1
2
3
C
A
2
1
D
F
A
M
F
B
问题三
问题二
问题四
D
A
2
4
5
7
1
3
6
8
C
B
E
F
1
A
D
E
C
B
A
B
C
D
1
A
B
A
C
3
2
D
2题
1题
3题
F
A
D
2题
B
E
3
5
1
4
2
5
8
7
6
2
4
1
3
b
3
5
2
1
4
4
5
1
3
2
a
4题
5题
6题
4
1
3
2
F
A
E
1
2
A
D
B
C
E
1题
2题
B
D
C
E
2
1
B
D
D
3
2
1
2
l
l1
l2
B
C
F
A
问题二
例1图
A
C
问题三
E
D
3
2
1
B
C
F
A
问题一
5
4
2
6
7
3
1
c
b
a
d
G
B
D
C
2
1
E
2
1
1
A
E
F
C
D
B
A
A
C
D
B
1题
2题
3题
5题
2
1
B
A
E
F
D
A
B
D
C
2
1
A
B
C
D
1题
C
3题
2题
2
3
1
5题
M
F
D
E
B
A
C
D
A
B
2
1
1
1
1
A
2
1
3
4
E
2
3
1
E
D
C
F
B
G
H
A
C
D
B
c
b
a
1题图
2题图
3题图
A
2
1
C
E
B
D
F
A
F
C
B
D
E
2
1
4
3
4题图
5题图
PAGE
班级: 组名: 组别: 姓名:
【学习目标】
1、认识对顶角。
2、理解对顶角相等这一性质。
3、能用“对顶角相等”这一性质解决一些简单的实际问题。
【重点难点】
重点:理解对顶角相等的性质并能运用
难点:对顶角的认识。
【学法指导】阅读教材160页——162页,
【知识链接】
补角和邻补角定义。
【学习过程】
知识点一:对顶角的概念
问题一:如图1,直线AB、CD相交于O,图中∠1和∠2的位置和数量关系分别是什么?如果还有存在这样关系的角,请找出来,并说明它们的位置关系和数量关系
问题二:如图1,直线AB、CD相交于O,图中∠1和∠3又有什么关系?如果还有存在这样关系的角,请找出来。
问题三:什么是对顶角?请找出图2中的对顶角。
问题四:如图3,直线AB、CD、EF相交于点O,图中共有几对对顶角?如果有条直线相交于点O,则有多少对对顶角?
知识点二:对顶角的性质
问题一:对顶角的性质是什么?
问题二:如图1,直线AB、CD相交于O,(1)若∠1=35°,则∠3= ,∠2=∠ = 。(2)若∠1=90°-α,∠3=39°,则α= °。
问题三:如图4,直线AB、CD、EF相交于点O,∠AOF=3∠BOF,∠AOC=90°,求∠EOC的度数。
问题四:如图5,已知直线AB、CD相交于点O,∠EOB=90°,OF平分∠AOD,∠AOC=26°30′,求∠COE,∠BOD,∠DOF,∠AOF的度数。
【基础训练】
1、下列说法正确的有( )
(1)对顶角相等;(2)相等的角是对顶角;(3)若两个角不相等,则这两个角一定不是对顶角;(4)若两个角不是对顶角,则这两个角不相等。
A、1个 B、2个 C、3个 D、4个
2、如图,直线AB和CD相交于点O,若∠AOD与∠BOC的和为230°,则∠AOC的度数为( ) A、65° B、75° C、55° D、45°
3、如图,直线、、相交于O,则下面四个选项正确的是( )
A、∠1=90°,∠2=30°,∠3=90°,∠4=60° B、∠1=∠3=90°,∠2=∠4=60°C、∠1=∠3=90°,∠2=∠4=30° D、∠1=∠3=90°∠2=60°,∠4=30°
4、如图,三条直线AB、CD、EF相交于同一点O,若∠AOE=2∠AOC,∠COF比∠AOE大30°,则∠AOC的度数是( )
A、30° B、60° C、20° D、45°
5、如图,直线AB和CD相交于点O,已知∠AOC=70°,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3,则∠EOD= 。
6、如图,直线AB和CD相交于点O,
∵∠1与∠2互补,∠2与∠3互补(已知)
∴∠1=∠3(同角的补角相等)
若∠1=50°,则∠2= ,∠3= ,∠4= ;
若∠1+∠3=80°,则∠1= ,∠2= ,∠3= ,∠4= 。
【课堂小结】
【当堂检测】
1、如图,直线BE、CF相交于O,OA、OD是射线,其中互为对顶角的是( )
A、∠AOE与∠COD B、∠AOD与∠BOD C、∠BOF与∠COE D、∠AOF与∠BOC
2、下列说法正确的是( )
A、如果两个角相等,那么这两个角是对顶角 B、有公共顶点的两个角是对顶角 C、有公共顶点并且相等的两个角是对顶角 D、如果两个角是对顶角,那么这两个角相等
3、如图,有两堵墙,要测量地面上所形成的∠AOB的度数,但人又不能进入围墙,只能站在墙外,如何测量?(用两种方法)
4、如图直线AB、CD相交于O,∠1=70°,OE平分∠AOD,求∠EOC和∠BOC的度数。
1、如图直线AB、CD相交于O,OB平分∠DOE,若∠DOE=60°,求∠AOC的度数
2、如图直线AB、CD相交于O,作∠DOE=∠BOD,OF平分∠AOE、∠AOC=28°,求∠EOF的度数。
《垂线》导学案
班级: 组名: 组别: 姓名:
【学习目标】
1、知道垂线、垂线段的定义和垂线的性质,体会点到直线的距离。
2、知道过一点有且只有一条直线垂直于已知直线,会用三角尺或量角器过一点画一条直线的垂线。
【重点难点】
垂线、垂线段、点到直线的距离的定义
【学法指导】阅读教材162页——165页,动手实验去检验教材中的结论
【知识链接】相交线及对顶角,跳远的测量方法
【学习过程】
知识点一:垂线
问题一:什么是垂直?请举例说明如何表示两条互相垂直的直线;什么是垂线?请画图说明;你能举例说出生活中垂线吗?
问题二:过一点如何画已知直线的垂线?有几种情况?请画图说明。
问题三:过一点画已知直线的垂线有几条?
问题四:如图,直线AB、CD相交于O,OE⊥CD,OF⊥AB,∠DOF=65°,求∠BOE和∠AOC的度数。
知识点二:垂线段
问题一:什么是垂线段?并画图说明。
问题二:什么是点到直线的距离?
问题三:如图,按要求画图:(1)点A到DC的距离AE;(2)连结AC,点B到AC的距离BF。
【基本训练】
1、下列说法正确的是( )
A、过一点有无数条直线与已知直线垂直 B、和一条直线垂直的直线有且只有一条C、过一点有且只有一条直线与已知直线垂直 D、两直线相交则必垂直
2、画一条线段的垂线,垂足在( )
A、线段上 B、线段的端点上 C、线段的延长线上 D、以上都有可能
3、如图,∠BAC=90°,AD⊥BC于D,则下面的结论正确的是( )
(1)线段AB是点B到AC的垂线段(2)线段AC是点C到AB的垂线段(3)线段AD是点D到BC的垂线段(4)线段BD是点B到AD的垂线段
A、1个 B、2个 C、3个 D、4个
4、如图直线AB、CD相交于O,OM⊥AB于O,且∠DOM=∠COM,求∠AOD的度数。
【当堂检测】
1、如果两条直线相交所成的四个角都是直角,那么两条直线互相 。
2、如图,OA⊥OC, ∠AOB: ∠AOC=2:3,∠BOC= 。
3、画线段AB的垂线有 条,过线段AB的中点P画线段AB的垂线有 条。
4、如图,已知三条直线AB、CD、EF相交于O,且EF⊥AB,(1)若
∠DOE=50°,则∠BOD= , ∠AOD= .(2)若∠COB=β,则∠BOD=
, ∠DOE= 。
5、如图,已知OA⊥m,OB⊥m,所以OA与OB重合,其理由是
( )A、过两点只有一条直线 B、过一点只能做一条垂线
C、经过一点只有一条直线垂直于已知直线 D、垂线段最短
【课堂小结】
现在你有哪些收获?
【拓展训练】
1、下列说法:(1)直线外一点与直线上各点的所有连线中,垂线段最短.(2)互为邻补角的两个角的平分线一定垂直。(3)两条直线相交,如果有两个角相等,那么这两条直线垂直。(4)两条直线相交,如果有3个角相等,那么这两条直线垂直。其中正确的有( )
A、1个 B、2个 C、3个 D、4个
2、直线m外一点P,它到直线m上点A、B、C的距离分别是6cm、3cm、5cm,则点P到直线的距离为( )
A、不大于3cm B、3cm C、5cm D、6cm
3、如图,三条直线相交于一点,若∠1: ∠2:∠3=1:2:3,求∠2.
《同位角、内错角、同旁内角》导学案
班级: 组名: 组别: 姓名:
【学习目标】
能根据图形判断哪些角是同位角、内错角、同旁内角。
【重点难点】
从不同图形重中找出不同位置关系的角
【知识链接】
对顶角及性质,邻补角
【学法指导】
阅读教材第166页——第168页,根据图形特点正确确定角的位置关系
【学习过程】
知识点一:同位角、内错角、同旁内角
问题一:什么同位角、内错角、同旁内角?
1、分别在两条直线的同侧,并且都在第三条直线的同旁,这样的两个角叫做 角,在两条直线之间,分别在第三条直线的两旁,这样的两个角叫做 角,在两条直线之间,并且在第三条直线的同旁,这样的两个角叫做 角。
2、如图,∠1与∠2是 角,∠1与∠3是 角,∠1与∠4是 角。
3、如图,∠5的同位角是 ,∠2的内错角是 ,∠3的同旁内角是 。
问题二:如图,∠1与∠B是 角,∠A与∠2是 角,∠ACD与 是内错角,∠BCD与∠B是 角,∠A与∠B是 角,∠ACE与∠3是 角。
问题三:如图,直线PQ与直线AB、射线MG交于点M,直线PQ与CD、EF交于点N,指出图中∠1与∠4,∠2与∠4,∠3与∠MNF是哪两条直线被哪一条直线截得的什么角?
【基本训练】
1、如图,同位角是( )
A、∠C和∠6,∠6和∠D B、∠2和∠3,∠1和∠D C、∠2和∠6,∠3和∠4 D、∠1和∠D,∠6和∠D
2、如图,图中与∠α是内错角关系的角有( )
A、1个 B、2个 C、3个 D、4个
3、如图,∠2的内错角是 ,∠3和∠B是 ,∠B的同旁内角是 。
4、如图,∠B与∠EAC是同位角,∠B与∠ACD是 ,∠EAC与∠ACD是同旁内角,∠BAC与∠ACD是 。
5、如图,直线AB、CD、EF两两相交,指出∠3与其他角(带数字标注)是什么关系的角?
【当堂检测】
1、如图,∠1和∠2是同位角的个数有( )
A、1个 B、2个 C、3个 D、4个
2、如图,下列说法错误的是( )
(1)∠1与∠3是同位角,(2)∠1与∠2是同位角,(3)∠1与∠2是同旁内角,(4)∠1与∠4是内错角
A、(1)和(2) B、(2)和(3) C、(2)和(4) D、(3)和(4)
3、如图,能与∠1构成同位角的角有( )
A、1个 B、2个 C、3个 D、4个
4、如图,与∠1成同位角的角有 个,与∠1成内错角的角有 个,与∠1成同旁内角的角有 个,
5、如图,∠1与∠2是直线 和直线 被第三条直线 所截而成的 角,∠2和∠3是直线 和直线 被第三条直线 所截而成的 角。
【课堂小结】
1、你有哪些收获?
2、还有什么疑惑?
【拓展训练】
1、如图,(1)∠1与∠3是直线 与直线 被直线 所截得到的
角。(2)∠2与∠3是直线 与直线 被直线 所截得到的 角。
2、如图,下列说法错误的是( )
A、∠1与∠2是内错角 B、∠2与∠4是对顶角
C、∠3与∠5是同旁内角 D、∠3与∠2是同位角
《平行线》导学案
班级: 组名: 组别: 姓名:
【学习目标】
1、知道平行线的定义,体会“平行公理”这个基本事实。
2、能画出已知直线的平行线。
【重点难点】
平行线的定义和平行公理
【学法指导】阅读教材169——170页,用动手操作试验的方法去学习。
【知识链接】
小学学过的平行知识以及生活中见过的平行
【学习过程】
知识点一:平行线
问题一:什么叫平行线?
问题二:下列说法中正确的是( ) A、不相交的两条直线时平行线 B、同一平面内,不相交的两条射线叫做平行线 C、在同一平面内,两条直线不相交就重合 D、同一平面内,没有公共点的两条直线时平行线
知识点二:平行公理
问题一:过直线外一点可以画多少条直线和这条直线平行?请动手画一画。
问题二:若两条直线都和第三条直线平行,则这两条直线有什么样的位置关系?
问题三:判断:
(1)不相交的两条直线是平行线 ( )
(2)过一点可以且只可以画一条直线与已知直线平行 ( )
(3)过相交直线AB、CD外一点E,作直线EF平行于AB且平行于CD( )
例3 已知:D是∠AOB内部一点,如图,过D作DE∥AO,作DF∥BO分别交OA、OB于F、E,画出图形,并说明四边形DEOF是什么图形?
【基本训练】
1、下列说法正确的是( )
A、在同一平面内,不重合的两条直线的位置关系只有相交、平行两种
B、在同一平面内,不相交的两条线段互相平行
C、不相交的两条直线是平行线
D、在同一平面内,不相交的两条射线互相平行
2、若a、b、c是三条直线,如果a∥b∥c,那么( )
A、a∥b B、a∥c C、a=c D、以上全不对
3、在同一平面内,两条直线的位置关系有 种,它们分别是 。
4、在同一平面内,与已知直线平行的直线有 条,过直线l外一点M与已知直线l平行的直线有 。
5、直线同侧有A、B、C三点,如果A、B两点确定的直线1与平行,B、C两点确定的直线????2也与平行,则A、B、C三点 其依据是 。
【课堂小结】
1、这节课有什么收获?
2、还有什么疑惑?
【当堂检测】
1、直线AB、CD、a、b在同一平面内,且AB∥CD,直线a与AB、CD都相交,直线b与AB、CD都相交,则直线a、b的位置关系是( )
A、相交 B、平行 C、垂直 D、相交或平行
2、若b∥c,a∥c,则 ∥ ,其理由是 。
3、如图在长方体中,互相平行的棱有 ,相交的棱有 ,既不平行也不相交的棱有 。(每空只需写出2组)。
4、在同一平面内,三条直线的交点最多是 个,最少是 个。
5、如图,AD∥BC,M是CD上的一点,在图中过点M画直线MN∥AD,则直线MN与BC的位置关系是 。
【拓展训练】
1、下列说法不正确的是( )A、过任意一点P可作已知直线L的一条平行线 B、同一平面内的两条不相交的直线是平行线 C、过直线外一点只能画一条直线与已知直线平行 D、平行于同一条直线的两条直线平行
2、如图,四边形ABCD和四边形AFCE都是平行四边形,点E、F分别在CD、AB上,则图中平行线的组数是( ) A、2 B、3 C、4 D、5
3、如图,(1)你能用学过的方法判断 a、b这两条直线的位置关系吗?
(2)过直线外一点A画直线c的平行线。(3)找出图中所有的平行线,并用“∥”表示。
《平行线的判定》导学案
班级: 组名: 组别: 姓名:
【学习目标】
1、知道平行线的三种判定方法,并能用这些方法判断两条直线是否平行。
2、学会一些简单的推理
【重点难点】
平行线的三种判定方法
【学法指导】阅读教材171——174页,通过动手试验去检验平行线的又一个基本事实
【知识链接】平行线和三线八角
【学习过程】
知识点一:平行线的判定方法
问题一:平行线的判定方法有哪些?
问题二:如图,(1)若∠1=∠2,则可以判定哪两条直线平行?说明理由
(2)若∠1=∠M,可判定哪两条直线平行?说明理由
(3)若∠C+∠A=180°,可判定哪两条直线平行?理由
问题三:如图,如果∠1=∠A,那么 ∥ ;若满足 ,则可得AD∥EF,(填一个即可)
问题四: 写出图中能使AB∥CD成立的各种条件。
【基本训练】
1、如图,如果∠1=∠2,那么根据 ,可得 ∥
;如果∠DAB+∠ABC=180°,那么根据 ,可得 ∥ ;如果∠3=∠B,那么根据 ,可得 ∥ 。
2、如图,∠1=70°,∠B=70°,∠C=130°,那么平行的直线是 。
3、如图,若使DE∥BC,则需要满足的条件是 (填一种)。
4、下列说法正确的个数是( ) (1)不相交的两条直线互相平行;(2)a∥b,b∥c,则a∥c;(3)在同一平面内,a⊥b,c⊥b,则a⊥c;(4)同旁内角相等,两直线平行。 A、1个 B、2个 C、3个 D、4个
【课堂小结】
你有什么收获?
你有什么新发现?
【当堂检测】
1、A、B是直线外不同的两点,直线a过点A,a⊥,直线b过点B,b⊥,则a、b的关系是( ) A、相交 B、平行 C、重合 D、平行或重合
2、如图,若∠1与∠2互补,∠2与∠4互补,则( )
A、3∥4 B、2∥5 C、1∥5 D、1∥3
3、两条直线被第三条直线所截,则( )
A、同位角必相等 B、内错角必相等 C、同旁内角必互补 D、以上结论均不对
4、如图,下列条件中不能判断直线1∥2的是( )
A、∠1=∠3 B、∠2=∠3 C、∠4=∠5 D、∠2+∠4=180°
5、如图,直线a、b被直线c所截,现在给出下列四个条件:(1)∠1=∠5;(2)∠1=∠3;(3)∠2+∠3=180°;(4)∠4=∠7,其中能判定a∥b的条件序号是( )
A、(1)(2) B、(1)(3) C、(1)(4) D、(3)(4)
6、如图(1)∵∠1= (已知),
∴DE∥ ;( )
(2)∵∠2= (已知)
∴EF∥ ;( )
(3)∵∠2= (已知)
∴BC∥ ;( )
(4)∵∠3+ =180°(已知)
∴BC∥ ;( )
【拓展训练】
1、如图,∠1=∠2,∠4=∠C,∠C+∠CDB=180°,求证:DE∥BF
2、如图,∠A=∠2, ∠E=∠1,AD⊥ED,那么AB∥CE吗?为什么?
《平行线的性质》导学案
班级: 组名: 组别: 姓名:
【学习目标】
1、知道平行线的三个性质。
2、能区别平行线的性质与平行线的识别,能用平行线的判定与性质解决问题。
3、体会推理过程,会用几何语言进行表达。
【重点难点】
1、平行线的性质
2、平行线的判定与性质的综合运用
【学法指导】
结合平行线的判定用类比的方法去阅读教材第175页——第178页,并用笔标注好重点难点的内容。
【知识链接】平行线的判定方法
【学习过程】
知识点一:平行线的性质
问题一:平行线的性质有哪些?
问题二:如图,l1∥l2,∠1=100°,那么∠2= .
问题三:如图,四边形ABCD为一个平行四边形,即AB∥CD,AD∥BC,则∠1与∠2的关系是 。
知识点二:平行线性质的运用
问题一: 如图AB∥DE,DF∥BC,∠1=62°,求∠2、∠3的度数。
问题二: 如图,已知直线a、b、c被直线d所截,若∠1=∠2,∠2+∠3=180°,
求证:∠1=∠7
【基本训练】
1、如图,(1)若AD∥BC,那么根据 ,可得∠1= ;(2)若AB∥CD,那么根据 ,可得∠1= 。
2、如图,AB∥CD, ∠1=40°,则∠2= 。
3、如图AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2= 。
4、如图,(1)若AD∥BC,那么根据两直线平行,同旁内角互补,可得∠ +
∠ABC=180°;(2)若AB∥CD,则由两直线平行,同旁内角互补,可得∠
+∠ABC=180°。
5、如图直线AB、CD被直线EF所截,若∠1=∠2,则∠AEF+∠CFE= 。
八、小结
你有哪些收获?
【当堂检测】
1、如图,AB∥CD,若∠2是∠1的2倍,则∠2等于( )
A、60° B、90 C、120° D、150°
2、已知:如图,直线∥,∠1=40°,那么∠2= 度。
3、如图,AB∥CD,AD∥BC,如果∠B=50°,那么∠D= 。
4、若点A在点B的北偏东40°方向,那么点B在点A的 方向。
5、如图,AD平分∠BAC,∠1=∠2,试说明∠1=∠M的理由。
【拓展练习】
1、如图,AB∥EF∥DC,EG∥DB,则图中与∠1相等的角(∠1除外)共有( )个
A、6 B、5 C、4 D、3
2、如图,若AB∥CD,则正确的是( )
A、∠1=∠2+∠3 B、∠1=∠2=∠3 C、∠1+∠2+∠3=180° D、∠1=∠2+∠3=180°
3、如图,a∥c,∠1=70°,∠2=110°,∠3=115°。求∠ 4的度数。
4、如图,若AC∥BD,∠1=∠4,则下列结论:(1)∠CAB=∠ABD,(2)AE∥BF,(3)∠2=∠3,(4)∠CAB=∠3+∠4,其中正确的有( )个。
A、1 B、2 C、3 D、4
5、如图,已知AD∥EF,若AD平分∠BAC,请说明∠1与∠2有何关系?
O
1
2
3
4
C
A
D
B
图1
F
E
D
C
B
A
H
G
图2
图3
D
C
F
E
B
O
A
A
图4
D
C
F
E
B
O
C
A
F
E
D
B
图5
A
D
C
B
A
2
O
E
4
3
1
C
D
B
A
第5题
第6题
第4题
O
A
E
F
B
D
C
60°
30°
4
3
2
1
C
C
C
C
D
B
A
第2题
第3题
B
A
O
C
1
O
D
E
A
B
B
E
C
O
D
A
A
C
O
D
E
F
B
C
O
F
D
B
E
A
A
B
C
D
A
B
D
C
A
C
M
B
D
2题图
C
O
B
A
C
A
E
D
B
F
O
4题图
B
A
O
m
3
2
1
P
4
1
M
3
2
N
3
2
1
B
A
D
E
C
C
E
Q
D
F
B
A
G
问题二图
问题三图
2
2
1
3
4
5
1
a
b
4
3
B
C
A
D
E
2题图
3题图
3
1
2
4题
3题
2题
1题
D
C
B
A
E
B
D
A
E
C
α
B
A
D
C
5
1
6
2
4
3
F
7
8
D
E
B
5
6
2
C
1
A
4
3
1
2
2
1
1
2
1
1
2
2
1
A
B
1
2
3
1
1
2
3
4
5
1
D
E
第2题
第3题
第4题
第5题
5
4
2
3
1
2
4
3
1
1题
2题
●D
O
A
B
A1
B1
C1
D1
A
C
D
B
A
B
C
D
M
●
3题
5题
a
b
B
F
C
A
E
D
A●
c
E
1
2
3
C
A
2
1
D
F
A
M
F
B
问题三
问题二
问题四
D
A
2
4
5
7
1
3
6
8
C
B
E
F
1
A
D
E
C
B
A
B
C
D
1
A
B
A
C
3
2
D
2题
1题
3题
F
A
D
2题
B
E
3
5
1
4
2
5
8
7
6
2
4
1
3
b
3
5
2
1
4
4
5
1
3
2
a
4题
5题
6题
4
1
3
2
F
A
E
1
2
A
D
B
C
E
1题
2题
B
D
C
E
2
1
B
D
D
3
2
1
2
l
l1
l2
B
C
F
A
问题二
例1图
A
C
问题三
E
D
3
2
1
B
C
F
A
问题一
5
4
2
6
7
3
1
c
b
a
d
G
B
D
C
2
1
E
2
1
1
A
E
F
C
D
B
A
A
C
D
B
1题
2题
3题
5题
2
1
B
A
E
F
D
A
B
D
C
2
1
A
B
C
D
1题
C
3题
2题
2
3
1
5题
M
F
D
E
B
A
C
D
A
B
2
1
1
1
1
A
2
1
3
4
E
2
3
1
E
D
C
F
B
G
H
A
C
D
B
c
b
a
1题图
2题图
3题图
A
2
1
C
E
B
D
F
A
F
C
B
D
E
2
1
4
3
4题图
5题图
PAGE
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
