人教新版七年级数学下学期《8.4 三元一次方程组的解法》2020年同步练习卷(解析版)
文档属性
| 名称 | 人教新版七年级数学下学期《8.4 三元一次方程组的解法》2020年同步练习卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 419.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-18 17:37:39 | ||
图片预览




文档简介
人教新版七年级下学期《8.4 三元一次方程组的解法》2020年同步练习卷
一.选择题(共3小题)
1.若2x+5y+4z=0,3x+y﹣7z=0,则x+y﹣z的值等于( )
A.0 B.1 C.2 D.不能求出
2.若(2x﹣4)2+(x+y)2+|4z﹣y|=0,则x+y+z等于( )
A.﹣ B. C.2 D.﹣2
3.有铅笔、练习本、圆珠笔三种学习用品,若购铅笔3支,练习本7本,圆珠笔1支共需3.15元;若购铅笔4支,练习本8本,圆珠笔2支共需4.2元,那么,购铅笔、练习本、圆珠笔各1件共需( )
A.1.2元 B.1.05元 C.0.95元 D.0.9元
二.填空题(共15小题)
4.已知:,则x+y+z= .
5.三元一次方程组的解是 .
6.如果x,y互为相反数,且满足|a﹣2y﹣3|+(5x+9)2=0,那么a= .
7.三元一次方程组的解是 .
8.已知x=﹣1时,3ax5﹣2bx3+cx2﹣2=10,其中a:b:c=2:3:6,那么= .
9.如果方程组的解是方程2x﹣3y+a=5的解,那么a的值是 .
10.若关于x的方程组的解满足x=y,则k= .
11.已知y=ax2+bx+c,且当x=1时,y=5;当x=﹣2时,y=14;当x=﹣3时,y=25,则a= ,b= ,c= .当x=4时,y= .
12.有甲、乙、丙三种货物,若购买甲3件、乙7件、丙1件,共315元;若购买甲4件、乙10件、丙1件,共420元,现在购买甲、乙、丙各1件,共需 元.
13.如图,长方形ABCD被分成8块,图中的数字是其中5块的面积数,则图中阴影部分的面积为 .
14.有甲、乙、丙3种商品,某人若购甲3件、乙7件、丙1件共需24元;若购甲4件、乙10件、丙1件共需33元,则此人购甲、乙、丙各一件共需 元.
15.7公斤桃子的价钱等于1公斤苹果和2公斤梨的价钱;7公斤苹果的价钱等于10公斤梨和1公斤桃子的价钱,则购买12公斤苹果所需的钱可以购买梨 公斤.
16.现有甲、乙、丙三种东西,若购买甲3件、乙5件、丙1件共需32元;若购买甲4件、乙7件、丙1件共需40元,则要购买甲、乙、丙各1件共需 元.
17.某公司董事会拨出总额为40万元款项作为奖励金,全部用于奖励本年度做出突出贡献的一、二、三等奖的职工.原来设定:一等奖每人5万元,二等奖每人3万元,三等奖每人2万元;后因考虑到一等奖的职工科技创新已给公司带来巨大的经济效益,现在改为:一等奖每人15万元,二等奖每人4方元,三等奖每人1万元,那么该公司本年度获得一、二、三等奖的职工共 人.
18.有A、B、C三种不同型号的电池,它们的价格各不相同.有一笔钱可买A型4只,B型18只,C型16只;或A型2只,B型15只,C型24只;或A型6只,B型12只,C型20只.如果将这笔钱全部用来购买C型号的电池,则能买 只.
三.解答题(共14小题)
19.二元一次方程组的解x,y的值相等,求k.
20.在y=ax2+bx+c中,当x=0时,y=﹣7;x=1时,y=﹣9;x=﹣1时,y=﹣3,求a、b、c的值.
21.已知关于x,y的方程组的解满足3x+2y=19,求m的值.
22.已知关于x,y的二元一次方程组的解x与y的值互为相反数,试求m的值.
23.已知:4x﹣3y﹣6z=0,x+2y﹣7z=0(xyz≠0),求的值.
24.解方程组.
25.已知方程组的解x、y的和为12,求n的值.
26.自习课上,数学老师为了检验小明同学对方程组这部分内容的掌握情况,给他出了这样一道练习:
“当m为何值时,方程组的解x、y互为相反数.”这下可把平时学习不认真的小明给难住了,聪明的同学,你能帮小明求出m的值吗?
27.若关于x、y的二元一次方程租的解x、y互为相反数,求m的值.
28.m为何值时,方程组的解x,y满足x﹣y=2,并求出此方程组的解.
29.解三元一次方程组:.
30.某农场300名职工耕种51公顷土地,计划种植水稻、棉花和蔬菜,已知种植农作物每公顷所需的劳动力人数及投入的设备资金如下表:
农作物品种 每公顷需劳动力 每公顷需投入资金
水稻 4人 1万元
棉花 8人 1万元
蔬菜 5人 2万元
已知该农场计划在设备投入67万元,应该怎样安排这三种作物的种植面积,才能使所有职工有工作,而且投入的资金正好够用?
31.为确保信息安全,在传输时往往需加密,发送方发出一组密码a,b,c时,则接收方对应收到的密码为A,B,C.双方约定:A=2a﹣b,B=2b,C=b+c,例如发出1,2,3,则收到0,4,5
(1)当发送方发出一组密码为2,3,5时,则接收方收到的密码是多少?
(2)当接收方收到一组密码2,8,11时,则发送方发出的密码是多少?
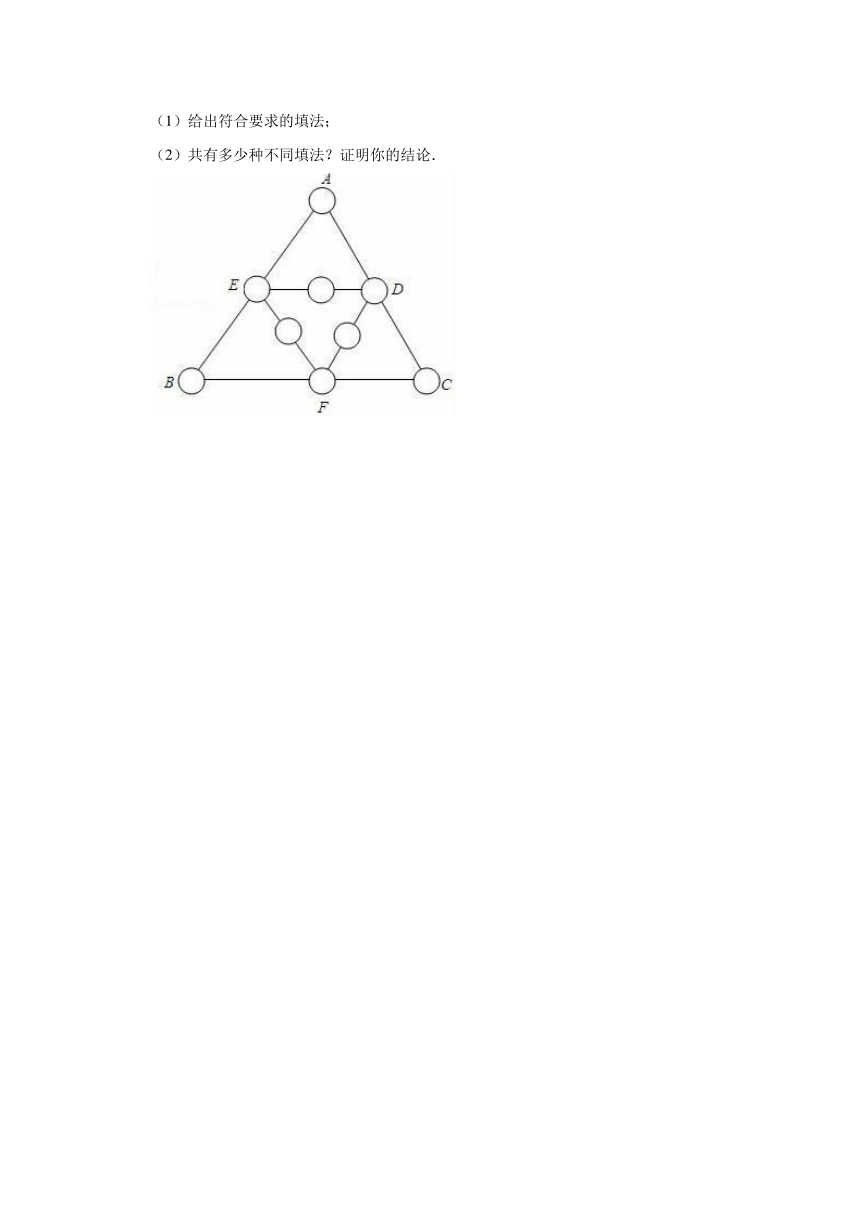
32.把数字1,2,3,…,9分别填入右图的9个圈内,要求三角形ABC和三角形DEF的每条边上三个圈内数位之和等于18.
(1)给出符合要求的填法;
(2)共有多少种不同填法?证明你的结论.
人教新版七年级下学期《8.4 三元一次方程组的解法》2020年同步练习卷
参考答案与试题解析
一.选择题(共3小题)
1.若2x+5y+4z=0,3x+y﹣7z=0,则x+y﹣z的值等于( )
A.0 B.1 C.2 D.不能求出
【分析】理解清楚题意,运用三元一次方程组的知识,把x,y用z表示出来,代入代数式求值.
【解答】解:根据题意得:,
把(2)变形为:y=7z﹣3x,
代入(1)得:x=3z,
代入(2)得:y=﹣2z,
则x+y﹣z=3z﹣2z﹣z=0.
故选:A.
【点评】本题的实质是解三元一次方程组,用加减法或代入法来解答.
2.若(2x﹣4)2+(x+y)2+|4z﹣y|=0,则x+y+z等于( )
A.﹣ B. C.2 D.﹣2
【分析】利用非负数的性质列出关于x,y及z的方程组,求出方程组的解即可得到x,y,z的值,确定出x+y+z的值.
【解答】解:∵(2x﹣4)2+(x+y)2+|4z﹣y|=0,
∴,
解得:,
则x+y+z=2﹣2﹣=﹣.
故选:A.
【点评】此题考查了解三元一次方程组,利用了消元的思想,熟练掌握运算法则是解本题的关键.
3.有铅笔、练习本、圆珠笔三种学习用品,若购铅笔3支,练习本7本,圆珠笔1支共需3.15元;若购铅笔4支,练习本8本,圆珠笔2支共需4.2元,那么,购铅笔、练习本、圆珠笔各1件共需( )
A.1.2元 B.1.05元 C.0.95元 D.0.9元
【分析】设购一支铅笔,一本练习本,一支圆珠笔分别需要x,y,z元,建立三元一次方程组,两个方程相减,即可求得x+y+z的值.
【解答】解:设购一支铅笔,一本练习本,一支圆珠笔分别需要x,y,z元,
根据题意得,
②﹣①得x+y+z=1.05(元).
故选:B.
【点评】解答此题的关键是根据题意列出方程组,同时还要有整体思想.
二.填空题(共15小题)
4.已知:,则x+y+z= 6 .
【分析】三个式子左右两边分别相加即可求解.
【解答】解:三个式子相加得:2(x+y+z)=12,
则x+y+z=6.
故答案是:6.
【点评】本题考查了三元一次方程组的解法,理解三个方程的左边相加所得结果与x+y+z的关系是关键.
5.三元一次方程组的解是 .
【分析】方程组利用加减消元法求出解即可.
【解答】解:,
①+②得:x﹣z=2④,
③+④得:2x=8,即x=4,
把x=4代入④得:z=2,
把z=2代入②得:y=3,
则方程组的解为,
故答案为:
【点评】此题考查了解三元一次方程组,利用了消元的思想,熟练掌握运算法则是解本题的关键.
6.如果x,y互为相反数,且满足|a﹣2y﹣3|+(5x+9)2=0,那么a= .
【分析】根据非负数的性质可得出两个关于x、y的方程,再联立x=﹣y组成方程组,可求得a的值.
【解答】解:根据题意得,解得.即a=.
【点评】初中阶段有三种类型的非负数:(1)绝对值;(2)偶次方;(3)二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0.根据这个结论可以求解这类题目.
7.三元一次方程组的解是 .
【分析】用代入法或加减消元法求出方程组的解即可.
【解答】解:(1)+(2)得3a+2b=15,
(1)﹣(3)得b=5,
代入3a+2b=15得a=,
把a=,b=5代入(1),
得c=.
故本题答案为:.
【点评】本题的实质是考查三元一次方程组的解法.需要对三元一次方程组的定义有一个深刻的理解.方程组有三个未知数,每个方程的未知项的次数都是1,并且一共有三个方程,像这样的方程组,叫三元一次方程组.通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.解题之前先观察方程组中的方程的系数特点,认准易消的未知数,消去未知数,组成元该未知数的二元一次方程组.
8.已知x=﹣1时,3ax5﹣2bx3+cx2﹣2=10,其中a:b:c=2:3:6,那么= .
【分析】先将x=﹣1代入3ax5﹣2bx3+cx2﹣2=10,得到一个关于a、b、c的方程,然后设a=2y,则b=3y,c=6y,代入即可求出y的值,继而求出a、b、c的值,最后代入即可求出答案.
【解答】解:将x=﹣1代入3ax5﹣2bx3+cx2﹣2=10,
得﹣3a+2b+c=12,
设a=2y,则b=3y,c=6y,
代入可得y=2,
即a=4,b=6,c=12,
代入===.
故答案为:.
【点评】本题考查了三元一次方程组解法,解题的关键是弄清题意,分别用y来表示a、b、c的值.
9.如果方程组的解是方程2x﹣3y+a=5的解,那么a的值是 ﹣10 .
【分析】本题实际上是一道关于三元一次方程组的题目,将题目中的二元一次方程组和三元一次方程列为三元一次方程组来解答即可.
【解答】解:由题意得
把(1)代入(2)得:
2(y+5)﹣y=5,(4)
解得y=﹣5;(5)
将(5)代入(1),解得x=0;(6)
把(5)(6)代入(3),解得a=﹣10.
【点评】理解清楚题意,运用三元一次方程组的知识,解出a的数值.
10.若关于x的方程组的解满足x=y,则k= .
【分析】理解清楚题意,运用三元一次方程组的知识,列出三元一次方程组,先用k表示出x的值,再代入原方程,求得k的值.
【解答】解:由题意得,
把③代入②得x=,
代入①得k=﹣.
故本题答案为:.
【点评】本题的实质是考查三元一次方程组的解法.需要对三元一次方程组的定义有一个深刻的理解.方程组有三个未知数,每个方程的未知项的次数都是1,并且一共有三个方程,像这样的方程组,叫三元一次方程组.通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.解题之前先观察方程组中的方程的系数特点,认准易消的未知数,消去未知数,组成元该未知数的二元一次方程组.
11.已知y=ax2+bx+c,且当x=1时,y=5;当x=﹣2时,y=14;当x=﹣3时,y=25,则a= 2 ,b= ﹣1 ,c= 4 .当x=4时,y= 32 .
【分析】根据题意,把x,y的值代入y=ax2+bx+c中,得到关于a、b、c的三元一次方程组,即可求得a、b、c的值.
【解答】解:据题意得,
解得,
∴当x=4时,y=32.
故本题答案为:4;32.
【点评】本题实质考查了三元一次方程组的建立和解法.此题提高了学生的计算能力.
12.有甲、乙、丙三种货物,若购买甲3件、乙7件、丙1件,共315元;若购买甲4件、乙10件、丙1件,共420元,现在购买甲、乙、丙各1件,共需 105 元.
【分析】设购买甲、乙、丙各一件分别需要x,y,z元,列出方程组,消去z后,得到x+3y的值,再代入①,即可求得x+y+z的值,也即购买甲、乙、丙各一件的共需钱数.
【解答】解:设购买甲、乙、丙各一件分别需要x,y,z元,
由题意得,
②﹣①得x+3y=105,
代入①得x+y+2(x+3y)+z=315,
即x+y+z+2×105=315,
∴x+y+z=315﹣210=105.
故答案为:105.
【点评】本题考查了三元一次方程组的实际应用,解答此题的关键是首先根据题意列出方程组,再整体求解.
13.如图,长方形ABCD被分成8块,图中的数字是其中5块的面积数,则图中阴影部分的面积为 85 .
【分析】设未知的三块面积分别为x,y,z(如图).根据S△BCF=S△ABF+S△CDF与S△ABE=S△ADE+S△BCE列出三元一次方程组,再利用加减消元法即可求得y的值.
【解答】解:设未知的三块面积分别为x,y,z(如图)
则,即
由①+②解得 y=85
故答案为85
【点评】解决本题的关键是理清三角形与矩形间的面积关系,列出三元一次方程组,再根据方程组中系数特点,通过加减,得到y值,即为所求.
14.有甲、乙、丙3种商品,某人若购甲3件、乙7件、丙1件共需24元;若购甲4件、乙10件、丙1件共需33元,则此人购甲、乙、丙各一件共需 6 元.
【分析】设甲、乙、丙3种商品的单价分别是x元、y元、z元.
由题意列方程组得:,然后求得x+y+z的值.
【解答】解:设甲、乙、丙3种商品的单价分别是x元、y元、z元.
由题意列方程组得
由①×3﹣②×2得 x+y+z=6
故答案为6.
【点评】根据系数特点,通过加减,得到一个整体,然后整体求解.
15.7公斤桃子的价钱等于1公斤苹果和2公斤梨的价钱;7公斤苹果的价钱等于10公斤梨和1公斤桃子的价钱,则购买12公斤苹果所需的钱可以购买梨 18 公斤.
【分析】设苹果的价格为每千克x元,梨的价格为每千克y元,桃子的价格为每千克z元,建立方程组,求得x,y的关系即可.
【解答】解:设苹果的价格为每千克x元,梨的价格为每千克y元,桃子的价格为每千克z元.
则根据题意列方程组,
解方程组得12x=18y.
∴买12千克苹果的钱可买18千克梨.
故本题答案为:18.
【点评】此题无法直接解出来,但通过关系式12x=18y可以轻松得出结论.
16.现有甲、乙、丙三种东西,若购买甲3件、乙5件、丙1件共需32元;若购买甲4件、乙7件、丙1件共需40元,则要购买甲、乙、丙各1件共需 16 元.
【分析】设甲、乙、丙每件单价为x、y、z元,建立方程组,整体求得x+y+z的值.
【解答】解:设甲、乙、丙每件单价为x、y、z元,
根据题意列方程组得,
②﹣①得:
x+2y=8③,
②+①得:
7x+12y+2z=72④,
④﹣③×5得:2x+2y+2z=32,
∴x+y+z=16.
故本题答案为:16.
【点评】未知数共有三个,方程只有两个,无法直接解答,通过加减,将x+y+z看做一个整体来解.
17.某公司董事会拨出总额为40万元款项作为奖励金,全部用于奖励本年度做出突出贡献的一、二、三等奖的职工.原来设定:一等奖每人5万元,二等奖每人3万元,三等奖每人2万元;后因考虑到一等奖的职工科技创新已给公司带来巨大的经济效益,现在改为:一等奖每人15万元,二等奖每人4方元,三等奖每人1万元,那么该公司本年度获得一、二、三等奖的职工共 17 人.
【分析】根据题中给出的条件列出两个三元一次方程,再根据X、Y、Z均为正整数,便可解得X+Y+Z的值.
【解答】解:设该公司本年底获得一、二、三等奖的职工分别是X,Y,Z人.
5X+3Y+2Z=40 (1)
15X+4Y+Z=40 (2)
(2)*2﹣(1)得5X+Y=8,
由于X,Y,Z为正整数,
0<5X<8,X=1,Y=3,从而得出Z=13.
X+Y+Z=17
该公司本年底获得一、二、三等奖的职工共17人.
故答案为:17.
【点评】本题主要考查了三元一次方程的实际应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键,属于中档题.
18.有A、B、C三种不同型号的电池,它们的价格各不相同.有一笔钱可买A型4只,B型18只,C型16只;或A型2只,B型15只,C型24只;或A型6只,B型12只,C型20只.如果将这笔钱全部用来购买C型号的电池,则能买 48 只.
【分析】先设买一只A型的价格是x元,买一只B型的价格是y元,买一只C型的价格是z元,能买C型W只根据题意列出方程组,求出方程组的解即可.
【解答】解:设买一只A型的价格是x元,买一只B型的价格是y元,买一只C型的价格是z元,能买C型W只,
根据题意得:,
解得:代入4x+18y+16z=Wz得:
W=48.
故答案为:48.
【点评】本题主要考查了三元一次方程组的应用问题,解答此题的关键是列出方程组,用代入消元法或加减消元法求出方程组的解.
三.解答题(共14小题)
19.二元一次方程组的解x,y的值相等,求k.
【分析】由于x=y,故把x=y代入第一个方程中,求得x的值,再代入第二个方程即可求得k的值.
【解答】解:由题意可知x=y,
∴4x+3y=7可化为4x+3x=7,
∴x=1,y=1.
将x=1,y=1代入kx+(k﹣1)y=3中得:
k+k﹣1=3,
∴k=2
【点评】由两个未知数的特殊关系,可将一个未知数用含另一个未知数的代数式代替,化“二元”为“一元”,从而求得两未知数的值.
20.在y=ax2+bx+c中,当x=0时,y=﹣7;x=1时,y=﹣9;x=﹣1时,y=﹣3,求a、b、c的值.
【分析】将x、y的值分别代入y=ax2+bx+c,转化为关于a、b、c的方程,再根据解三元一次方程组的步骤,即可求出a、b、c的值.
【解答】解:由题意得:,
把c=0代入②、③得:,
解得:a=1,b=﹣3,
则a=1,b=﹣3,c=﹣7.
【点评】此题考查了三元一次方程组的解,掌握解三元一次方程组的步骤是本题的关键,主要渗透了待定系数法求函数解析式的思想.
21.已知关于x,y的方程组的解满足3x+2y=19,求m的值.
【分析】先解关于x,y二元一次方程组,求得用m表示的x,y的值后,再代入3x+2y=19,建立关于m的方程,解出m的数值.
【解答】解:,
①+②得x=7m,
①﹣②得y=﹣m,
依题意得3×7m+2×(﹣m)=19,
∴m=1.
【点评】本题实质是解二元一次方程组,先用m表示的x,y的值后,再求解关于m的方程,解方程组关键是消元.
22.已知关于x,y的二元一次方程组的解x与y的值互为相反数,试求m的值.
【分析】根据三元一次方程组解的概念,列出三元一次方程组解出x,y的值代入含有m的式子即求出m的值.
【解答】解:由题意得,
由③得:x=﹣y,④
把④代入①得,y=﹣m﹣3,
把④代入②得:x=,
∴﹣m﹣3+=0,
解得m=﹣10.
【点评】本题的实质是考查三元一次方程组的解法.通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.
23.已知:4x﹣3y﹣6z=0,x+2y﹣7z=0(xyz≠0),求的值.
【分析】先由题意列出方程组,先用z表示出x,y的值,再代入所求代数式求值即可.
【解答】解:由题意得,
①﹣②×4得:
﹣11y+22z=0,
解得:y=2z,
将y=2z代入①得:x=3z,
即,
代入得:
原式==.
【点评】将x、y都转化为关于z的代数式,即可将z消去,得原式的值.
24.解方程组.
【分析】利用加减法消掉一个未知数,将三元一次方程组转化为二元一次方程组,再进行解答.
【解答】解:
③+①得,3x+5y=11④,
③×2+②得,3x+3y=9⑤,
④﹣⑤得2y=2,y=1,
将y=1代入⑤得,3x=6,
x=2,
将x=2,y=1代入①得,z=6﹣2×2﹣3×1=﹣1,
∴方程组的解为.
【点评】本题考查了解三元一次方程组,需要对三元一次方程组的定义有一个深刻的理解.方程组有三个未知数,每个方程的未知项的次数都是1,并且一共有三个方程,像这样的方程组,叫三元一次方程组.通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.解题之前先观察方程组中的方程的系数特点,认准易消的未知数,消去未知数,得到由另外两个未知数组成的二元一次方程组.
25.已知方程组的解x、y的和为12,求n的值.
【分析】由题意列出方程组求解,用n表示出x,y的值代入x+y=12,求得n的值.
【解答】解:由题意可得,
解得,
代入x+y=12,
得n=14.
【点评】本题的实质是解三元一次方程组,用加减法或代入法来解答.
26.自习课上,数学老师为了检验小明同学对方程组这部分内容的掌握情况,给他出了这样一道练习:
“当m为何值时,方程组的解x、y互为相反数.”这下可把平时学习不认真的小明给难住了,聪明的同学,你能帮小明求出m的值吗?
【分析】理解清楚题意,运用三元一次方程组的知识,解出m的数值.
【解答】解:因为x、y互为相反数,所以方程组可变形为:,
解得:.
故m=2.
【点评】解答此题关键是根据题列出方程组,再用代入法或加减消元法求解.
27.若关于x、y的二元一次方程租的解x、y互为相反数,求m的值.
【分析】利用x,y的关系代入方程组消元,从而求得m的值.
【解答】解:将x=﹣y代入二元一次方程租可得关于y,m的二元一次方程组,解得m=23.
【点评】考查了解二元一次方程的能力和对方程解的概念的理解.
28.m为何值时,方程组的解x,y满足x﹣y=2,并求出此方程组的解.
【分析】先用含m的代数式表示x,y,即解关于x,y的方程组,再代入x﹣y=2中可得m的值,进而求出方程组的解.
【解答】解:解方程组得,
∵x﹣y=2,
∴﹣(﹣)=2,
解得:m=1,
∴方程组的解是.
【点评】本题的实质是考查三元一次方程组的解法.需要对三元一次方程组的定义有一个深刻的理解.方程组有三个未知数,每个方程的未知项的次数都是1,并且一共有三个方程,像这样的方程组,叫三元一次方程组.通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.解题之前先观察方程组中的方程的系数特点,认准易消的未知数,消去未知数,组成元该未知数的二元一次方程组.
29.解三元一次方程组:.
【分析】因为三个方程中z的系数相同或互为相反数,应用加减法来解.
【解答】解:①+②得5x+2y=16④,
③+②得3x+4y=18⑤,
得方程组,
解得,
代入③得,2+3+z=6,
∴z=1.
∴方程组的解为.
【点评】解三元一次方程组要注意以下几点:
方程组有三个未知数,每个方程的未知项的次数都是1,并且一共有三个方程,像这样的方程组,叫三元一次方程组.通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.解题之前先观察方程组中的方程的系数特点,认准易消的未知数,消去未知数,组成元该未知数的二元一次方程组.
30.某农场300名职工耕种51公顷土地,计划种植水稻、棉花和蔬菜,已知种植农作物每公顷所需的劳动力人数及投入的设备资金如下表:
农作物品种 每公顷需劳动力 每公顷需投入资金
水稻 4人 1万元
棉花 8人 1万元
蔬菜 5人 2万元
已知该农场计划在设备投入67万元,应该怎样安排这三种作物的种植面积,才能使所有职工有工作,而且投入的资金正好够用?
【分析】首先种植水稻x公顷,棉花y公顷,蔬菜为z公顷,根据题意可得等量关系:①三种农作物的投入资金=67万元;②三种农作物所需要的人力=300名职工;③三种农作物的公顷数=51公顷,根据等量关系列出方程组即可.
【解答】解:设种植水稻x公顷,棉花y公顷,蔬菜为z公顷,由题意得:
,
解得:,
答:种植水稻15公顷,棉花20公顷,蔬菜为16公顷.
【点评】此题主要考查了三元一次方程组的应用,关键是弄懂题意,抓住题目中的关键语句,找出等量关系,设出未知数,列出方程组.
31.为确保信息安全,在传输时往往需加密,发送方发出一组密码a,b,c时,则接收方对应收到的密码为A,B,C.双方约定:A=2a﹣b,B=2b,C=b+c,例如发出1,2,3,则收到0,4,5
(1)当发送方发出一组密码为2,3,5时,则接收方收到的密码是多少?
(2)当接收方收到一组密码2,8,11时,则发送方发出的密码是多少?
【分析】(1)根据题意可得方程组,再解方程组即可.
(2)根据题意可得方程组,再解方程组即可.
【解答】解:(1)由题意得:,
解得:A=1,B=6,C=8,
答:接收方收到的密码是1、6、8;
(2)由题意得:,
解得:a=3,b=4,c=7,
答:发送方发出的密码是3、4、7.
【点评】此题主要考查了方程组的应用,关键是正确理解题意,根据密文与明文之间的关系列出方程组.
32.把数字1,2,3,…,9分别填入右图的9个圈内,要求三角形ABC和三角形DEF的每条边上三个圈内数位之和等于18.
(1)给出符合要求的填法;
(2)共有多少种不同填法?证明你的结论.
【分析】(1)先确定D、E、F三处的数字之和应该是24,再进一步分析其它的数字;
(2)把填入A,B,C三处圈内的三个数之和记为x;D,E,F三处圈内的三个数之和记为y;其余三个圈所填的数位之和为z.结合图形和已知条件得到方程组,进而求得y=24,再进一步分析即可.
【解答】解:(1)右图给出了一个符合要求的填法;
(2)共有6种不同填法
把填入A,B,C三处圈内的三个数之和记为x;D,E,F三处圈内的三个数之和记为y;其余三个圈所填的数位之和为z.显然有x+y+z=1+2+…+9=45①,
图中六条边,每条边上三个圈中之数的和为18,所以有z+3y+2x=6×18=108②,
②﹣①,得x+2y=108﹣45=63③,
把AB,BC,CA每一边上三个圈中的数的和相加,则可得2x+y=3×18=54④,
联立③,④,解得x=15,y=24,
继而解之z=6.
在1,2,3,…,9中三个数之和为24的仅为7,8,9,所以在D,E,F三处圈内,只能填7,8,9三个数,共有6种不同填法.
显然,当这三个圈中的数一旦确定,根据题目要求,其余六个圈内的数也随之确定,从而得结论,共有6种不同的填法.
【点评】此题中要特别注意三角形的顶点的数字的重复使用,能够根据各边的数字之和列方程组求解.
一.选择题(共3小题)
1.若2x+5y+4z=0,3x+y﹣7z=0,则x+y﹣z的值等于( )
A.0 B.1 C.2 D.不能求出
2.若(2x﹣4)2+(x+y)2+|4z﹣y|=0,则x+y+z等于( )
A.﹣ B. C.2 D.﹣2
3.有铅笔、练习本、圆珠笔三种学习用品,若购铅笔3支,练习本7本,圆珠笔1支共需3.15元;若购铅笔4支,练习本8本,圆珠笔2支共需4.2元,那么,购铅笔、练习本、圆珠笔各1件共需( )
A.1.2元 B.1.05元 C.0.95元 D.0.9元
二.填空题(共15小题)
4.已知:,则x+y+z= .
5.三元一次方程组的解是 .
6.如果x,y互为相反数,且满足|a﹣2y﹣3|+(5x+9)2=0,那么a= .
7.三元一次方程组的解是 .
8.已知x=﹣1时,3ax5﹣2bx3+cx2﹣2=10,其中a:b:c=2:3:6,那么= .
9.如果方程组的解是方程2x﹣3y+a=5的解,那么a的值是 .
10.若关于x的方程组的解满足x=y,则k= .
11.已知y=ax2+bx+c,且当x=1时,y=5;当x=﹣2时,y=14;当x=﹣3时,y=25,则a= ,b= ,c= .当x=4时,y= .
12.有甲、乙、丙三种货物,若购买甲3件、乙7件、丙1件,共315元;若购买甲4件、乙10件、丙1件,共420元,现在购买甲、乙、丙各1件,共需 元.
13.如图,长方形ABCD被分成8块,图中的数字是其中5块的面积数,则图中阴影部分的面积为 .
14.有甲、乙、丙3种商品,某人若购甲3件、乙7件、丙1件共需24元;若购甲4件、乙10件、丙1件共需33元,则此人购甲、乙、丙各一件共需 元.
15.7公斤桃子的价钱等于1公斤苹果和2公斤梨的价钱;7公斤苹果的价钱等于10公斤梨和1公斤桃子的价钱,则购买12公斤苹果所需的钱可以购买梨 公斤.
16.现有甲、乙、丙三种东西,若购买甲3件、乙5件、丙1件共需32元;若购买甲4件、乙7件、丙1件共需40元,则要购买甲、乙、丙各1件共需 元.
17.某公司董事会拨出总额为40万元款项作为奖励金,全部用于奖励本年度做出突出贡献的一、二、三等奖的职工.原来设定:一等奖每人5万元,二等奖每人3万元,三等奖每人2万元;后因考虑到一等奖的职工科技创新已给公司带来巨大的经济效益,现在改为:一等奖每人15万元,二等奖每人4方元,三等奖每人1万元,那么该公司本年度获得一、二、三等奖的职工共 人.
18.有A、B、C三种不同型号的电池,它们的价格各不相同.有一笔钱可买A型4只,B型18只,C型16只;或A型2只,B型15只,C型24只;或A型6只,B型12只,C型20只.如果将这笔钱全部用来购买C型号的电池,则能买 只.
三.解答题(共14小题)
19.二元一次方程组的解x,y的值相等,求k.
20.在y=ax2+bx+c中,当x=0时,y=﹣7;x=1时,y=﹣9;x=﹣1时,y=﹣3,求a、b、c的值.
21.已知关于x,y的方程组的解满足3x+2y=19,求m的值.
22.已知关于x,y的二元一次方程组的解x与y的值互为相反数,试求m的值.
23.已知:4x﹣3y﹣6z=0,x+2y﹣7z=0(xyz≠0),求的值.
24.解方程组.
25.已知方程组的解x、y的和为12,求n的值.
26.自习课上,数学老师为了检验小明同学对方程组这部分内容的掌握情况,给他出了这样一道练习:
“当m为何值时,方程组的解x、y互为相反数.”这下可把平时学习不认真的小明给难住了,聪明的同学,你能帮小明求出m的值吗?
27.若关于x、y的二元一次方程租的解x、y互为相反数,求m的值.
28.m为何值时,方程组的解x,y满足x﹣y=2,并求出此方程组的解.
29.解三元一次方程组:.
30.某农场300名职工耕种51公顷土地,计划种植水稻、棉花和蔬菜,已知种植农作物每公顷所需的劳动力人数及投入的设备资金如下表:
农作物品种 每公顷需劳动力 每公顷需投入资金
水稻 4人 1万元
棉花 8人 1万元
蔬菜 5人 2万元
已知该农场计划在设备投入67万元,应该怎样安排这三种作物的种植面积,才能使所有职工有工作,而且投入的资金正好够用?
31.为确保信息安全,在传输时往往需加密,发送方发出一组密码a,b,c时,则接收方对应收到的密码为A,B,C.双方约定:A=2a﹣b,B=2b,C=b+c,例如发出1,2,3,则收到0,4,5
(1)当发送方发出一组密码为2,3,5时,则接收方收到的密码是多少?
(2)当接收方收到一组密码2,8,11时,则发送方发出的密码是多少?
32.把数字1,2,3,…,9分别填入右图的9个圈内,要求三角形ABC和三角形DEF的每条边上三个圈内数位之和等于18.
(1)给出符合要求的填法;
(2)共有多少种不同填法?证明你的结论.
人教新版七年级下学期《8.4 三元一次方程组的解法》2020年同步练习卷
参考答案与试题解析
一.选择题(共3小题)
1.若2x+5y+4z=0,3x+y﹣7z=0,则x+y﹣z的值等于( )
A.0 B.1 C.2 D.不能求出
【分析】理解清楚题意,运用三元一次方程组的知识,把x,y用z表示出来,代入代数式求值.
【解答】解:根据题意得:,
把(2)变形为:y=7z﹣3x,
代入(1)得:x=3z,
代入(2)得:y=﹣2z,
则x+y﹣z=3z﹣2z﹣z=0.
故选:A.
【点评】本题的实质是解三元一次方程组,用加减法或代入法来解答.
2.若(2x﹣4)2+(x+y)2+|4z﹣y|=0,则x+y+z等于( )
A.﹣ B. C.2 D.﹣2
【分析】利用非负数的性质列出关于x,y及z的方程组,求出方程组的解即可得到x,y,z的值,确定出x+y+z的值.
【解答】解:∵(2x﹣4)2+(x+y)2+|4z﹣y|=0,
∴,
解得:,
则x+y+z=2﹣2﹣=﹣.
故选:A.
【点评】此题考查了解三元一次方程组,利用了消元的思想,熟练掌握运算法则是解本题的关键.
3.有铅笔、练习本、圆珠笔三种学习用品,若购铅笔3支,练习本7本,圆珠笔1支共需3.15元;若购铅笔4支,练习本8本,圆珠笔2支共需4.2元,那么,购铅笔、练习本、圆珠笔各1件共需( )
A.1.2元 B.1.05元 C.0.95元 D.0.9元
【分析】设购一支铅笔,一本练习本,一支圆珠笔分别需要x,y,z元,建立三元一次方程组,两个方程相减,即可求得x+y+z的值.
【解答】解:设购一支铅笔,一本练习本,一支圆珠笔分别需要x,y,z元,
根据题意得,
②﹣①得x+y+z=1.05(元).
故选:B.
【点评】解答此题的关键是根据题意列出方程组,同时还要有整体思想.
二.填空题(共15小题)
4.已知:,则x+y+z= 6 .
【分析】三个式子左右两边分别相加即可求解.
【解答】解:三个式子相加得:2(x+y+z)=12,
则x+y+z=6.
故答案是:6.
【点评】本题考查了三元一次方程组的解法,理解三个方程的左边相加所得结果与x+y+z的关系是关键.
5.三元一次方程组的解是 .
【分析】方程组利用加减消元法求出解即可.
【解答】解:,
①+②得:x﹣z=2④,
③+④得:2x=8,即x=4,
把x=4代入④得:z=2,
把z=2代入②得:y=3,
则方程组的解为,
故答案为:
【点评】此题考查了解三元一次方程组,利用了消元的思想,熟练掌握运算法则是解本题的关键.
6.如果x,y互为相反数,且满足|a﹣2y﹣3|+(5x+9)2=0,那么a= .
【分析】根据非负数的性质可得出两个关于x、y的方程,再联立x=﹣y组成方程组,可求得a的值.
【解答】解:根据题意得,解得.即a=.
【点评】初中阶段有三种类型的非负数:(1)绝对值;(2)偶次方;(3)二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0.根据这个结论可以求解这类题目.
7.三元一次方程组的解是 .
【分析】用代入法或加减消元法求出方程组的解即可.
【解答】解:(1)+(2)得3a+2b=15,
(1)﹣(3)得b=5,
代入3a+2b=15得a=,
把a=,b=5代入(1),
得c=.
故本题答案为:.
【点评】本题的实质是考查三元一次方程组的解法.需要对三元一次方程组的定义有一个深刻的理解.方程组有三个未知数,每个方程的未知项的次数都是1,并且一共有三个方程,像这样的方程组,叫三元一次方程组.通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.解题之前先观察方程组中的方程的系数特点,认准易消的未知数,消去未知数,组成元该未知数的二元一次方程组.
8.已知x=﹣1时,3ax5﹣2bx3+cx2﹣2=10,其中a:b:c=2:3:6,那么= .
【分析】先将x=﹣1代入3ax5﹣2bx3+cx2﹣2=10,得到一个关于a、b、c的方程,然后设a=2y,则b=3y,c=6y,代入即可求出y的值,继而求出a、b、c的值,最后代入即可求出答案.
【解答】解:将x=﹣1代入3ax5﹣2bx3+cx2﹣2=10,
得﹣3a+2b+c=12,
设a=2y,则b=3y,c=6y,
代入可得y=2,
即a=4,b=6,c=12,
代入===.
故答案为:.
【点评】本题考查了三元一次方程组解法,解题的关键是弄清题意,分别用y来表示a、b、c的值.
9.如果方程组的解是方程2x﹣3y+a=5的解,那么a的值是 ﹣10 .
【分析】本题实际上是一道关于三元一次方程组的题目,将题目中的二元一次方程组和三元一次方程列为三元一次方程组来解答即可.
【解答】解:由题意得
把(1)代入(2)得:
2(y+5)﹣y=5,(4)
解得y=﹣5;(5)
将(5)代入(1),解得x=0;(6)
把(5)(6)代入(3),解得a=﹣10.
【点评】理解清楚题意,运用三元一次方程组的知识,解出a的数值.
10.若关于x的方程组的解满足x=y,则k= .
【分析】理解清楚题意,运用三元一次方程组的知识,列出三元一次方程组,先用k表示出x的值,再代入原方程,求得k的值.
【解答】解:由题意得,
把③代入②得x=,
代入①得k=﹣.
故本题答案为:.
【点评】本题的实质是考查三元一次方程组的解法.需要对三元一次方程组的定义有一个深刻的理解.方程组有三个未知数,每个方程的未知项的次数都是1,并且一共有三个方程,像这样的方程组,叫三元一次方程组.通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.解题之前先观察方程组中的方程的系数特点,认准易消的未知数,消去未知数,组成元该未知数的二元一次方程组.
11.已知y=ax2+bx+c,且当x=1时,y=5;当x=﹣2时,y=14;当x=﹣3时,y=25,则a= 2 ,b= ﹣1 ,c= 4 .当x=4时,y= 32 .
【分析】根据题意,把x,y的值代入y=ax2+bx+c中,得到关于a、b、c的三元一次方程组,即可求得a、b、c的值.
【解答】解:据题意得,
解得,
∴当x=4时,y=32.
故本题答案为:4;32.
【点评】本题实质考查了三元一次方程组的建立和解法.此题提高了学生的计算能力.
12.有甲、乙、丙三种货物,若购买甲3件、乙7件、丙1件,共315元;若购买甲4件、乙10件、丙1件,共420元,现在购买甲、乙、丙各1件,共需 105 元.
【分析】设购买甲、乙、丙各一件分别需要x,y,z元,列出方程组,消去z后,得到x+3y的值,再代入①,即可求得x+y+z的值,也即购买甲、乙、丙各一件的共需钱数.
【解答】解:设购买甲、乙、丙各一件分别需要x,y,z元,
由题意得,
②﹣①得x+3y=105,
代入①得x+y+2(x+3y)+z=315,
即x+y+z+2×105=315,
∴x+y+z=315﹣210=105.
故答案为:105.
【点评】本题考查了三元一次方程组的实际应用,解答此题的关键是首先根据题意列出方程组,再整体求解.
13.如图,长方形ABCD被分成8块,图中的数字是其中5块的面积数,则图中阴影部分的面积为 85 .
【分析】设未知的三块面积分别为x,y,z(如图).根据S△BCF=S△ABF+S△CDF与S△ABE=S△ADE+S△BCE列出三元一次方程组,再利用加减消元法即可求得y的值.
【解答】解:设未知的三块面积分别为x,y,z(如图)
则,即
由①+②解得 y=85
故答案为85
【点评】解决本题的关键是理清三角形与矩形间的面积关系,列出三元一次方程组,再根据方程组中系数特点,通过加减,得到y值,即为所求.
14.有甲、乙、丙3种商品,某人若购甲3件、乙7件、丙1件共需24元;若购甲4件、乙10件、丙1件共需33元,则此人购甲、乙、丙各一件共需 6 元.
【分析】设甲、乙、丙3种商品的单价分别是x元、y元、z元.
由题意列方程组得:,然后求得x+y+z的值.
【解答】解:设甲、乙、丙3种商品的单价分别是x元、y元、z元.
由题意列方程组得
由①×3﹣②×2得 x+y+z=6
故答案为6.
【点评】根据系数特点,通过加减,得到一个整体,然后整体求解.
15.7公斤桃子的价钱等于1公斤苹果和2公斤梨的价钱;7公斤苹果的价钱等于10公斤梨和1公斤桃子的价钱,则购买12公斤苹果所需的钱可以购买梨 18 公斤.
【分析】设苹果的价格为每千克x元,梨的价格为每千克y元,桃子的价格为每千克z元,建立方程组,求得x,y的关系即可.
【解答】解:设苹果的价格为每千克x元,梨的价格为每千克y元,桃子的价格为每千克z元.
则根据题意列方程组,
解方程组得12x=18y.
∴买12千克苹果的钱可买18千克梨.
故本题答案为:18.
【点评】此题无法直接解出来,但通过关系式12x=18y可以轻松得出结论.
16.现有甲、乙、丙三种东西,若购买甲3件、乙5件、丙1件共需32元;若购买甲4件、乙7件、丙1件共需40元,则要购买甲、乙、丙各1件共需 16 元.
【分析】设甲、乙、丙每件单价为x、y、z元,建立方程组,整体求得x+y+z的值.
【解答】解:设甲、乙、丙每件单价为x、y、z元,
根据题意列方程组得,
②﹣①得:
x+2y=8③,
②+①得:
7x+12y+2z=72④,
④﹣③×5得:2x+2y+2z=32,
∴x+y+z=16.
故本题答案为:16.
【点评】未知数共有三个,方程只有两个,无法直接解答,通过加减,将x+y+z看做一个整体来解.
17.某公司董事会拨出总额为40万元款项作为奖励金,全部用于奖励本年度做出突出贡献的一、二、三等奖的职工.原来设定:一等奖每人5万元,二等奖每人3万元,三等奖每人2万元;后因考虑到一等奖的职工科技创新已给公司带来巨大的经济效益,现在改为:一等奖每人15万元,二等奖每人4方元,三等奖每人1万元,那么该公司本年度获得一、二、三等奖的职工共 17 人.
【分析】根据题中给出的条件列出两个三元一次方程,再根据X、Y、Z均为正整数,便可解得X+Y+Z的值.
【解答】解:设该公司本年底获得一、二、三等奖的职工分别是X,Y,Z人.
5X+3Y+2Z=40 (1)
15X+4Y+Z=40 (2)
(2)*2﹣(1)得5X+Y=8,
由于X,Y,Z为正整数,
0<5X<8,X=1,Y=3,从而得出Z=13.
X+Y+Z=17
该公司本年底获得一、二、三等奖的职工共17人.
故答案为:17.
【点评】本题主要考查了三元一次方程的实际应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键,属于中档题.
18.有A、B、C三种不同型号的电池,它们的价格各不相同.有一笔钱可买A型4只,B型18只,C型16只;或A型2只,B型15只,C型24只;或A型6只,B型12只,C型20只.如果将这笔钱全部用来购买C型号的电池,则能买 48 只.
【分析】先设买一只A型的价格是x元,买一只B型的价格是y元,买一只C型的价格是z元,能买C型W只根据题意列出方程组,求出方程组的解即可.
【解答】解:设买一只A型的价格是x元,买一只B型的价格是y元,买一只C型的价格是z元,能买C型W只,
根据题意得:,
解得:代入4x+18y+16z=Wz得:
W=48.
故答案为:48.
【点评】本题主要考查了三元一次方程组的应用问题,解答此题的关键是列出方程组,用代入消元法或加减消元法求出方程组的解.
三.解答题(共14小题)
19.二元一次方程组的解x,y的值相等,求k.
【分析】由于x=y,故把x=y代入第一个方程中,求得x的值,再代入第二个方程即可求得k的值.
【解答】解:由题意可知x=y,
∴4x+3y=7可化为4x+3x=7,
∴x=1,y=1.
将x=1,y=1代入kx+(k﹣1)y=3中得:
k+k﹣1=3,
∴k=2
【点评】由两个未知数的特殊关系,可将一个未知数用含另一个未知数的代数式代替,化“二元”为“一元”,从而求得两未知数的值.
20.在y=ax2+bx+c中,当x=0时,y=﹣7;x=1时,y=﹣9;x=﹣1时,y=﹣3,求a、b、c的值.
【分析】将x、y的值分别代入y=ax2+bx+c,转化为关于a、b、c的方程,再根据解三元一次方程组的步骤,即可求出a、b、c的值.
【解答】解:由题意得:,
把c=0代入②、③得:,
解得:a=1,b=﹣3,
则a=1,b=﹣3,c=﹣7.
【点评】此题考查了三元一次方程组的解,掌握解三元一次方程组的步骤是本题的关键,主要渗透了待定系数法求函数解析式的思想.
21.已知关于x,y的方程组的解满足3x+2y=19,求m的值.
【分析】先解关于x,y二元一次方程组,求得用m表示的x,y的值后,再代入3x+2y=19,建立关于m的方程,解出m的数值.
【解答】解:,
①+②得x=7m,
①﹣②得y=﹣m,
依题意得3×7m+2×(﹣m)=19,
∴m=1.
【点评】本题实质是解二元一次方程组,先用m表示的x,y的值后,再求解关于m的方程,解方程组关键是消元.
22.已知关于x,y的二元一次方程组的解x与y的值互为相反数,试求m的值.
【分析】根据三元一次方程组解的概念,列出三元一次方程组解出x,y的值代入含有m的式子即求出m的值.
【解答】解:由题意得,
由③得:x=﹣y,④
把④代入①得,y=﹣m﹣3,
把④代入②得:x=,
∴﹣m﹣3+=0,
解得m=﹣10.
【点评】本题的实质是考查三元一次方程组的解法.通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.
23.已知:4x﹣3y﹣6z=0,x+2y﹣7z=0(xyz≠0),求的值.
【分析】先由题意列出方程组,先用z表示出x,y的值,再代入所求代数式求值即可.
【解答】解:由题意得,
①﹣②×4得:
﹣11y+22z=0,
解得:y=2z,
将y=2z代入①得:x=3z,
即,
代入得:
原式==.
【点评】将x、y都转化为关于z的代数式,即可将z消去,得原式的值.
24.解方程组.
【分析】利用加减法消掉一个未知数,将三元一次方程组转化为二元一次方程组,再进行解答.
【解答】解:
③+①得,3x+5y=11④,
③×2+②得,3x+3y=9⑤,
④﹣⑤得2y=2,y=1,
将y=1代入⑤得,3x=6,
x=2,
将x=2,y=1代入①得,z=6﹣2×2﹣3×1=﹣1,
∴方程组的解为.
【点评】本题考查了解三元一次方程组,需要对三元一次方程组的定义有一个深刻的理解.方程组有三个未知数,每个方程的未知项的次数都是1,并且一共有三个方程,像这样的方程组,叫三元一次方程组.通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.解题之前先观察方程组中的方程的系数特点,认准易消的未知数,消去未知数,得到由另外两个未知数组成的二元一次方程组.
25.已知方程组的解x、y的和为12,求n的值.
【分析】由题意列出方程组求解,用n表示出x,y的值代入x+y=12,求得n的值.
【解答】解:由题意可得,
解得,
代入x+y=12,
得n=14.
【点评】本题的实质是解三元一次方程组,用加减法或代入法来解答.
26.自习课上,数学老师为了检验小明同学对方程组这部分内容的掌握情况,给他出了这样一道练习:
“当m为何值时,方程组的解x、y互为相反数.”这下可把平时学习不认真的小明给难住了,聪明的同学,你能帮小明求出m的值吗?
【分析】理解清楚题意,运用三元一次方程组的知识,解出m的数值.
【解答】解:因为x、y互为相反数,所以方程组可变形为:,
解得:.
故m=2.
【点评】解答此题关键是根据题列出方程组,再用代入法或加减消元法求解.
27.若关于x、y的二元一次方程租的解x、y互为相反数,求m的值.
【分析】利用x,y的关系代入方程组消元,从而求得m的值.
【解答】解:将x=﹣y代入二元一次方程租可得关于y,m的二元一次方程组,解得m=23.
【点评】考查了解二元一次方程的能力和对方程解的概念的理解.
28.m为何值时,方程组的解x,y满足x﹣y=2,并求出此方程组的解.
【分析】先用含m的代数式表示x,y,即解关于x,y的方程组,再代入x﹣y=2中可得m的值,进而求出方程组的解.
【解答】解:解方程组得,
∵x﹣y=2,
∴﹣(﹣)=2,
解得:m=1,
∴方程组的解是.
【点评】本题的实质是考查三元一次方程组的解法.需要对三元一次方程组的定义有一个深刻的理解.方程组有三个未知数,每个方程的未知项的次数都是1,并且一共有三个方程,像这样的方程组,叫三元一次方程组.通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.解题之前先观察方程组中的方程的系数特点,认准易消的未知数,消去未知数,组成元该未知数的二元一次方程组.
29.解三元一次方程组:.
【分析】因为三个方程中z的系数相同或互为相反数,应用加减法来解.
【解答】解:①+②得5x+2y=16④,
③+②得3x+4y=18⑤,
得方程组,
解得,
代入③得,2+3+z=6,
∴z=1.
∴方程组的解为.
【点评】解三元一次方程组要注意以下几点:
方程组有三个未知数,每个方程的未知项的次数都是1,并且一共有三个方程,像这样的方程组,叫三元一次方程组.通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.解题之前先观察方程组中的方程的系数特点,认准易消的未知数,消去未知数,组成元该未知数的二元一次方程组.
30.某农场300名职工耕种51公顷土地,计划种植水稻、棉花和蔬菜,已知种植农作物每公顷所需的劳动力人数及投入的设备资金如下表:
农作物品种 每公顷需劳动力 每公顷需投入资金
水稻 4人 1万元
棉花 8人 1万元
蔬菜 5人 2万元
已知该农场计划在设备投入67万元,应该怎样安排这三种作物的种植面积,才能使所有职工有工作,而且投入的资金正好够用?
【分析】首先种植水稻x公顷,棉花y公顷,蔬菜为z公顷,根据题意可得等量关系:①三种农作物的投入资金=67万元;②三种农作物所需要的人力=300名职工;③三种农作物的公顷数=51公顷,根据等量关系列出方程组即可.
【解答】解:设种植水稻x公顷,棉花y公顷,蔬菜为z公顷,由题意得:
,
解得:,
答:种植水稻15公顷,棉花20公顷,蔬菜为16公顷.
【点评】此题主要考查了三元一次方程组的应用,关键是弄懂题意,抓住题目中的关键语句,找出等量关系,设出未知数,列出方程组.
31.为确保信息安全,在传输时往往需加密,发送方发出一组密码a,b,c时,则接收方对应收到的密码为A,B,C.双方约定:A=2a﹣b,B=2b,C=b+c,例如发出1,2,3,则收到0,4,5
(1)当发送方发出一组密码为2,3,5时,则接收方收到的密码是多少?
(2)当接收方收到一组密码2,8,11时,则发送方发出的密码是多少?
【分析】(1)根据题意可得方程组,再解方程组即可.
(2)根据题意可得方程组,再解方程组即可.
【解答】解:(1)由题意得:,
解得:A=1,B=6,C=8,
答:接收方收到的密码是1、6、8;
(2)由题意得:,
解得:a=3,b=4,c=7,
答:发送方发出的密码是3、4、7.
【点评】此题主要考查了方程组的应用,关键是正确理解题意,根据密文与明文之间的关系列出方程组.
32.把数字1,2,3,…,9分别填入右图的9个圈内,要求三角形ABC和三角形DEF的每条边上三个圈内数位之和等于18.
(1)给出符合要求的填法;
(2)共有多少种不同填法?证明你的结论.
【分析】(1)先确定D、E、F三处的数字之和应该是24,再进一步分析其它的数字;
(2)把填入A,B,C三处圈内的三个数之和记为x;D,E,F三处圈内的三个数之和记为y;其余三个圈所填的数位之和为z.结合图形和已知条件得到方程组,进而求得y=24,再进一步分析即可.
【解答】解:(1)右图给出了一个符合要求的填法;
(2)共有6种不同填法
把填入A,B,C三处圈内的三个数之和记为x;D,E,F三处圈内的三个数之和记为y;其余三个圈所填的数位之和为z.显然有x+y+z=1+2+…+9=45①,
图中六条边,每条边上三个圈中之数的和为18,所以有z+3y+2x=6×18=108②,
②﹣①,得x+2y=108﹣45=63③,
把AB,BC,CA每一边上三个圈中的数的和相加,则可得2x+y=3×18=54④,
联立③,④,解得x=15,y=24,
继而解之z=6.
在1,2,3,…,9中三个数之和为24的仅为7,8,9,所以在D,E,F三处圈内,只能填7,8,9三个数,共有6种不同填法.
显然,当这三个圈中的数一旦确定,根据题目要求,其余六个圈内的数也随之确定,从而得结论,共有6种不同的填法.
【点评】此题中要特别注意三角形的顶点的数字的重复使用,能够根据各边的数字之和列方程组求解.
