人教版七年级数学下册第五章相交线与平行线知识整理与同步练习(附答案)
文档属性
| 名称 | 人教版七年级数学下册第五章相交线与平行线知识整理与同步练习(附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 822.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-19 00:00:00 | ||
图片预览



文档简介
? 七年级数学下册第五章知识整理
知识梳理
1.两个角有一条公共边,它们的另一条边互为反向延长线,具有这样位置关系的两个角,互为___________.
2.两个角有一个公共顶点,并且一个角的两边分别是另一个角两边的反向延长线,具有这种位置关系的角,互为___________.对顶角的性质:___________.
3.垂直是相交的一种特殊情形,两条直线互相垂直,其中的一条直线叫做另一条直线的___________,它们的交点叫做___________。
4.在同一平面内,过一点有且只有___________直线与已知直线垂直。
5.连接直线外一点与直线上各点的所有线段中,___________最短,简单说成:
___________。
6.直线外一点到这条直线的垂线段的长度,叫做___________。
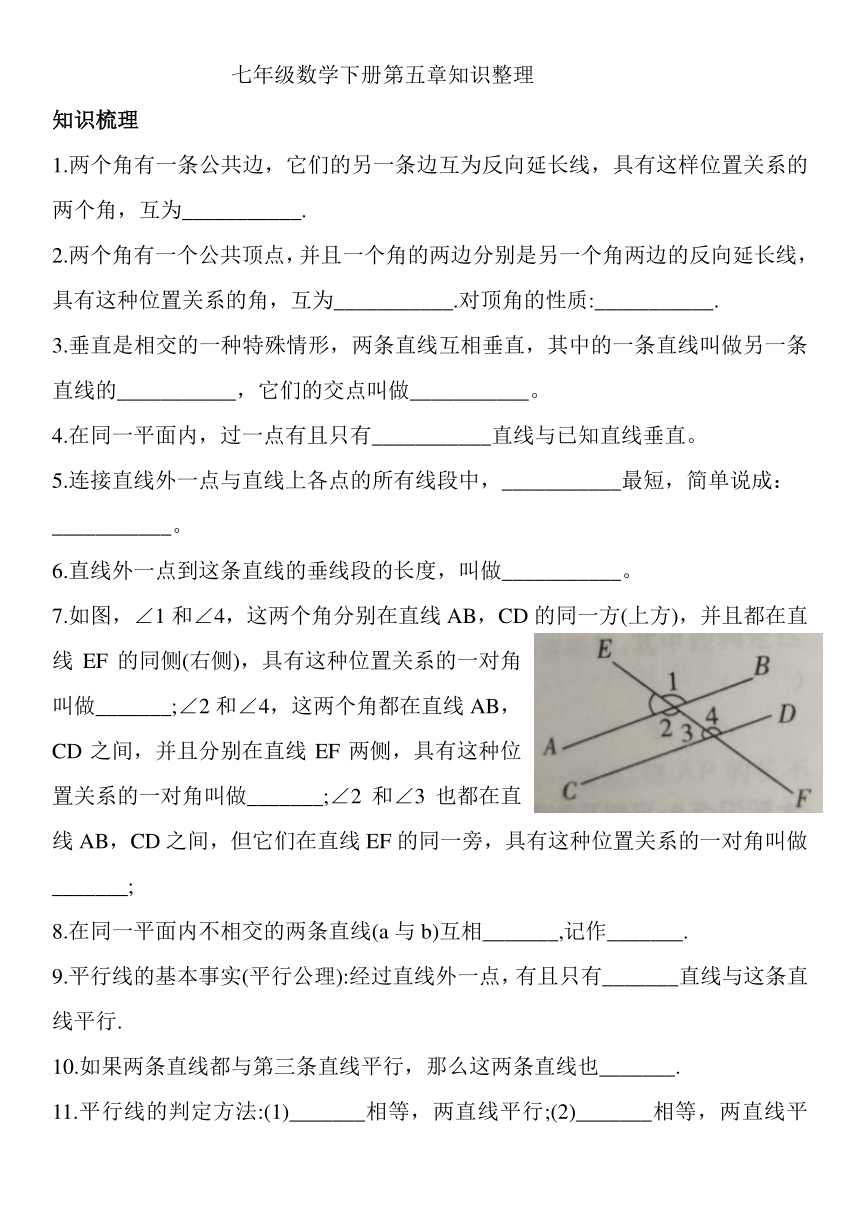
7.如图,∠1和∠4,这两个角分别在直线AB,CD的同一方(上方),并且都在直线EF的同侧(右侧),具有这种位置关系的一对角叫做_______;∠2和∠4,这两个角都在直线AB,CD之间,并且分别在直线EF两侧,具有这种位置关系的一对角叫做_______;∠2和∠3也都在直线AB,CD之间,但它们在直线EF的同一旁,具有这种位置关系的一对角叫做
_______;
8.在同一平面内不相交的两条直线(a与b)互相_______,记作_______.
9.平行线的基本事实(平行公理):经过直线外一点,有且只有_______直线与这条直线平行.
10.如果两条直线都与第三条直线平行,那么这两条直线也_______.
11.平行线的判定方法:(1)_______相等,两直线平行;(2)_______相等,两直线平行;(3)_______互补,两直线平行。
12.平行线的性质:(1)两直线平行,同位角_______;(2)两直线平行,内错角_______;
(3)两直线平行,同旁内角_______.
13.判断一件事情的语句,叫做_______.经过推理证实的真命题叫做_______.
14.在很多情况下,一个命题的正确性需要经过推理才能作出判断,这个推理过程叫做_______.
15.平移得到的新图形与原图形的形状和大小_______.
知识反馈
★知识点1;邻补角与对顶角
1.下列说法正确的是 ( )
A.和为180°的角为邻补角 B和为180°的两个角为邻补角
C,有公共顶点,和为90°的角为邻补角
D.有公共顶点和一条公共边,它们的另一边互为反向廷长线的两个角为邻补角
2.如图,∠1和∠2是对顶角的是 ( )
3.如图,直线AB、CD相交于点O,若∠AOC=(3x+10°),∠BOC=(2x-10°),求∠AOD的度数.
★知识点2:垂线与垂线段
4.过直线AB外一点P画直线AB的垂线,则 ( )
A.能画无数条 B只能画2条 C.只能画1条 D.不能画成
5.在数学课上,同学们在练习过点B作线段AC所在直线的垂线段时,有一部分
同学画出下列四种图形,请你数一数,错误的个数为( )
A.1个 B.2个 C.3个 D.4个
6.如图,在体育测试中,裁判员测量某同学的跳远成绩,在直线上的A、B、C三点中,点________到沙坑中脚印点P的距离为该同学的成绩.
如图,在三角形ABC中,∠BCA=90°,CD⊥AB,垂足为点D.线段AB,BC,CD的大小关系如何?并说明理由.
★知识点3:同位角、内错角、同旁内角
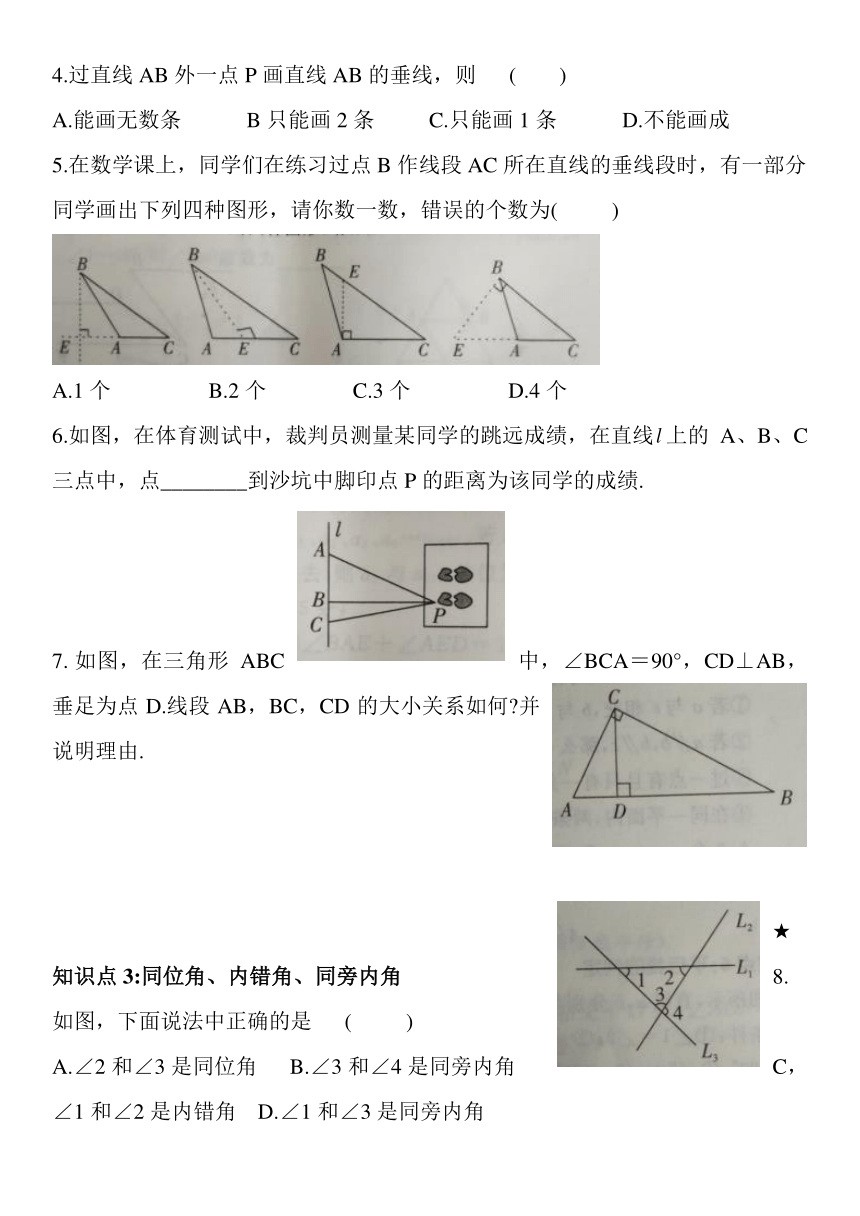
8.如图,下面说法中正确的是 ( )
A.∠2和∠3是同位角 B.∠3和∠4是同旁内角
C,∠1和∠2是内错角 D.∠1和∠3是同旁内角
9.如图所示,直线DE、BC被直线AB所截,∠1与∠4是_________,∠2与∠4是_________,∠1与∠2是_________,∠3与∠4是_________.
★知识点4:平行线的定义及画法
10.下列生活中的线是平行线的有 ( )
①铁路上并排的两条铁轨;②上体育课时,双杠的两个横杠;③滑雪时两只雪撬滑动轨迹;④操场上的升旗杆与教室屋梁。
A.1个 D.2个 C.3个 D.4个
11.读句画图
(1)M是直线AB外一点,过点M的直线MN与AB交于点N,过点M画直线CD,使CD∥AB。
(2)点P是∠ABC的边AB上的一点,直线EF经过点P,且与直线BC平行。
★知识点5:平行线的一个基本事实及其推论
12.下列说法中,错误的有 ( )
①若a与c相交,b与c相交,则a与b相交 ②若a∥b,b∥c,那么a∥c
③过一点有且只有一条直线与已知直线平行
④在同一平面内,两条直线的位置关系有平行、相交、垂直三种
A.3个 B.2个 C.1个 D.0个
13.如图,PC∥AB,QC∥AB,则点P,C,Q在同一条直线上,理由是:__________
___________________________________________________________________
★知识点6:平行线的判定
14.如图所示,直线a,b分别与直线相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠8=180°;④∠5+∠7=180°.其中能判定a∥b的条件是( )
A.①③ B.②④ C.③④① D.①②③④
15.如图所示,推理填空:
(1)∵∠1=________(已知),
∴AC∥ED(同位角相等,两直线平行)
(2)∵∠2=________(已知),
∴AB∥FD(内错角相等,两直线平行)
(3)∵∠2+________=180°(已知),
∴AC∥ED(同旁内角互补,两直线平行)
16.如图,已知∠ACD=70°,∠ACB=60°,∠ABC=50°,试说明:AB∥CD。
如图,已知∠BED=∠B+∠D,试说明AB与CD的位置关系。
★知识点7:平行线的性质
18.如图,AB∥CD,∠CED=90°,∠AEC=35°,则∠D的大小为( ).
A.65° B.55° C.45° D.35°
19.如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=________.
20.如图所示,直线a⊥直线c,直线b⊥直线c,若∠1=65°,则∠2=________.
21.如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
★知识点8:命题、定理、证明
22.已知下列命题:①相等的角是对顶角;②互补的角就是平角;③互补的两个角一定是一个锐角和一个钝角;④平行于同一条直线的两直线平行:⑤邻补角的角平分线互相垂直,其中,正确命题的个数为 ( )
A.0个 B.1个 C.2个 D.3个
23.如图所示,OP平分∠MON,A,B分别在OP,OM上,∠BOA=∠BAO.求证:AB∥ON.
★知识点9:平移及利用平移作图
24.下面的各组图案中,不能由其中一个经平移后得到另一个的是( )
25.在如图所示的方格纸中,平移所给的图案,使点A移到点A的位置.
参考答案
知识梳理
1.邻补角 2.对顶角 对顶角相等 3.垂线 垂足 4.一条 5.垂线段 垂线段最短 6.点到直线的距离 7.同位角 内错角 同旁内角 8.平行 a∥b
一条 10.互相平行 11同位角 内错角 同旁内角 12.相等 相等 互补 13.命题 定理 14.证明 15.完全相同
知识反馈
1.D 2.C
3.解∵∠AOC+∠BOC=180°,∴(3x+10)+(2x-10)=180,解得x=36,∴∠AOD=∠BOC=(2×36-10)°=62°
4.C? 5C? 6.B
7.解:AB>BC>CD.理由:因为点C与直线AB上各点的连线中,CD是垂线段,故线段CD最短,所以BC>CD.因为点B与直线AC上各点的连线中,BC是垂线段,故线段BC最短,所以AB>BC.所以AB>BC>CD
8,D 9.同位角 内错角 对顶角 同旁内角 10.C
11
12.A 13.过直线外一点有且只有一条直线与这条直线平行 14.D
15.∠C ∠BED ∠AFD
16.解:∵∠ACD=70°,∠ACB=60°,∴∠BCD=130°,∵∠ABC=50°,∴∠BCD+∠ABC=180°,∴AB∥CD(同旁内角互补,两直线平行)
17.解:AB∥CD,理由如下:在∠BED内部作射线EF,使∠BEF=∠B,则AB∥EF(内错角相等,两直线平行),∵∠BED=∠BEF+∠FED=∠B+∠D,∴∠FED=∠D,∴CD∥EF(内错角相等,两直线平行),∴AB∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
18.B 19.63°30' 20.65°
21.解:∵AB∥CF,∠ABC=70°,∴∠BCF=∠ABC=70°(两直线平行,内错角相等)又∵DE∥CF,∠CDE=130°,∴∠DCF+∠CDE=180°(两直线平行,同旁内角互补).∴∠DCF=50°,∴∠BCD=∠BCF﹣∠DCF=70°-50°=20°
22.C 23.证明:∵OP平分∠MON(已知),∴∠AOB=∠AON(角平分线的定义).又∵∠BOA=∠BAO(已知),∴∠BAO=∠AON(等量代换),∴AB∥ON(内错角相等,两直线平行)
24.C 25.图略
知识梳理
1.两个角有一条公共边,它们的另一条边互为反向延长线,具有这样位置关系的两个角,互为___________.
2.两个角有一个公共顶点,并且一个角的两边分别是另一个角两边的反向延长线,具有这种位置关系的角,互为___________.对顶角的性质:___________.
3.垂直是相交的一种特殊情形,两条直线互相垂直,其中的一条直线叫做另一条直线的___________,它们的交点叫做___________。
4.在同一平面内,过一点有且只有___________直线与已知直线垂直。
5.连接直线外一点与直线上各点的所有线段中,___________最短,简单说成:
___________。
6.直线外一点到这条直线的垂线段的长度,叫做___________。
7.如图,∠1和∠4,这两个角分别在直线AB,CD的同一方(上方),并且都在直线EF的同侧(右侧),具有这种位置关系的一对角叫做_______;∠2和∠4,这两个角都在直线AB,CD之间,并且分别在直线EF两侧,具有这种位置关系的一对角叫做_______;∠2和∠3也都在直线AB,CD之间,但它们在直线EF的同一旁,具有这种位置关系的一对角叫做
_______;
8.在同一平面内不相交的两条直线(a与b)互相_______,记作_______.
9.平行线的基本事实(平行公理):经过直线外一点,有且只有_______直线与这条直线平行.
10.如果两条直线都与第三条直线平行,那么这两条直线也_______.
11.平行线的判定方法:(1)_______相等,两直线平行;(2)_______相等,两直线平行;(3)_______互补,两直线平行。
12.平行线的性质:(1)两直线平行,同位角_______;(2)两直线平行,内错角_______;
(3)两直线平行,同旁内角_______.
13.判断一件事情的语句,叫做_______.经过推理证实的真命题叫做_______.
14.在很多情况下,一个命题的正确性需要经过推理才能作出判断,这个推理过程叫做_______.
15.平移得到的新图形与原图形的形状和大小_______.
知识反馈
★知识点1;邻补角与对顶角
1.下列说法正确的是 ( )
A.和为180°的角为邻补角 B和为180°的两个角为邻补角
C,有公共顶点,和为90°的角为邻补角
D.有公共顶点和一条公共边,它们的另一边互为反向廷长线的两个角为邻补角
2.如图,∠1和∠2是对顶角的是 ( )
3.如图,直线AB、CD相交于点O,若∠AOC=(3x+10°),∠BOC=(2x-10°),求∠AOD的度数.
★知识点2:垂线与垂线段
4.过直线AB外一点P画直线AB的垂线,则 ( )
A.能画无数条 B只能画2条 C.只能画1条 D.不能画成
5.在数学课上,同学们在练习过点B作线段AC所在直线的垂线段时,有一部分
同学画出下列四种图形,请你数一数,错误的个数为( )
A.1个 B.2个 C.3个 D.4个
6.如图,在体育测试中,裁判员测量某同学的跳远成绩,在直线上的A、B、C三点中,点________到沙坑中脚印点P的距离为该同学的成绩.
如图,在三角形ABC中,∠BCA=90°,CD⊥AB,垂足为点D.线段AB,BC,CD的大小关系如何?并说明理由.
★知识点3:同位角、内错角、同旁内角
8.如图,下面说法中正确的是 ( )
A.∠2和∠3是同位角 B.∠3和∠4是同旁内角
C,∠1和∠2是内错角 D.∠1和∠3是同旁内角
9.如图所示,直线DE、BC被直线AB所截,∠1与∠4是_________,∠2与∠4是_________,∠1与∠2是_________,∠3与∠4是_________.
★知识点4:平行线的定义及画法
10.下列生活中的线是平行线的有 ( )
①铁路上并排的两条铁轨;②上体育课时,双杠的两个横杠;③滑雪时两只雪撬滑动轨迹;④操场上的升旗杆与教室屋梁。
A.1个 D.2个 C.3个 D.4个
11.读句画图
(1)M是直线AB外一点,过点M的直线MN与AB交于点N,过点M画直线CD,使CD∥AB。
(2)点P是∠ABC的边AB上的一点,直线EF经过点P,且与直线BC平行。
★知识点5:平行线的一个基本事实及其推论
12.下列说法中,错误的有 ( )
①若a与c相交,b与c相交,则a与b相交 ②若a∥b,b∥c,那么a∥c
③过一点有且只有一条直线与已知直线平行
④在同一平面内,两条直线的位置关系有平行、相交、垂直三种
A.3个 B.2个 C.1个 D.0个
13.如图,PC∥AB,QC∥AB,则点P,C,Q在同一条直线上,理由是:__________
___________________________________________________________________
★知识点6:平行线的判定
14.如图所示,直线a,b分别与直线相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠8=180°;④∠5+∠7=180°.其中能判定a∥b的条件是( )
A.①③ B.②④ C.③④① D.①②③④
15.如图所示,推理填空:
(1)∵∠1=________(已知),
∴AC∥ED(同位角相等,两直线平行)
(2)∵∠2=________(已知),
∴AB∥FD(内错角相等,两直线平行)
(3)∵∠2+________=180°(已知),
∴AC∥ED(同旁内角互补,两直线平行)
16.如图,已知∠ACD=70°,∠ACB=60°,∠ABC=50°,试说明:AB∥CD。
如图,已知∠BED=∠B+∠D,试说明AB与CD的位置关系。
★知识点7:平行线的性质
18.如图,AB∥CD,∠CED=90°,∠AEC=35°,则∠D的大小为( ).
A.65° B.55° C.45° D.35°
19.如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=________.
20.如图所示,直线a⊥直线c,直线b⊥直线c,若∠1=65°,则∠2=________.
21.如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
★知识点8:命题、定理、证明
22.已知下列命题:①相等的角是对顶角;②互补的角就是平角;③互补的两个角一定是一个锐角和一个钝角;④平行于同一条直线的两直线平行:⑤邻补角的角平分线互相垂直,其中,正确命题的个数为 ( )
A.0个 B.1个 C.2个 D.3个
23.如图所示,OP平分∠MON,A,B分别在OP,OM上,∠BOA=∠BAO.求证:AB∥ON.
★知识点9:平移及利用平移作图
24.下面的各组图案中,不能由其中一个经平移后得到另一个的是( )
25.在如图所示的方格纸中,平移所给的图案,使点A移到点A的位置.
参考答案
知识梳理
1.邻补角 2.对顶角 对顶角相等 3.垂线 垂足 4.一条 5.垂线段 垂线段最短 6.点到直线的距离 7.同位角 内错角 同旁内角 8.平行 a∥b
一条 10.互相平行 11同位角 内错角 同旁内角 12.相等 相等 互补 13.命题 定理 14.证明 15.完全相同
知识反馈
1.D 2.C
3.解∵∠AOC+∠BOC=180°,∴(3x+10)+(2x-10)=180,解得x=36,∴∠AOD=∠BOC=(2×36-10)°=62°
4.C? 5C? 6.B
7.解:AB>BC>CD.理由:因为点C与直线AB上各点的连线中,CD是垂线段,故线段CD最短,所以BC>CD.因为点B与直线AC上各点的连线中,BC是垂线段,故线段BC最短,所以AB>BC.所以AB>BC>CD
8,D 9.同位角 内错角 对顶角 同旁内角 10.C
11
12.A 13.过直线外一点有且只有一条直线与这条直线平行 14.D
15.∠C ∠BED ∠AFD
16.解:∵∠ACD=70°,∠ACB=60°,∴∠BCD=130°,∵∠ABC=50°,∴∠BCD+∠ABC=180°,∴AB∥CD(同旁内角互补,两直线平行)
17.解:AB∥CD,理由如下:在∠BED内部作射线EF,使∠BEF=∠B,则AB∥EF(内错角相等,两直线平行),∵∠BED=∠BEF+∠FED=∠B+∠D,∴∠FED=∠D,∴CD∥EF(内错角相等,两直线平行),∴AB∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
18.B 19.63°30' 20.65°
21.解:∵AB∥CF,∠ABC=70°,∴∠BCF=∠ABC=70°(两直线平行,内错角相等)又∵DE∥CF,∠CDE=130°,∴∠DCF+∠CDE=180°(两直线平行,同旁内角互补).∴∠DCF=50°,∴∠BCD=∠BCF﹣∠DCF=70°-50°=20°
22.C 23.证明:∵OP平分∠MON(已知),∴∠AOB=∠AON(角平分线的定义).又∵∠BOA=∠BAO(已知),∴∠BAO=∠AON(等量代换),∴AB∥ON(内错角相等,两直线平行)
24.C 25.图略
