人教新版七年级数学下学期《10.2 直方图》2020年同步练习卷(解析版)
文档属性
| 名称 | 人教新版七年级数学下学期《10.2 直方图》2020年同步练习卷(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 447.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-18 00:00:00 | ||
图片预览




文档简介
人教新版七年级下学期《10.2 直方图》2020年同步练习卷
一.选择题(共4小题)
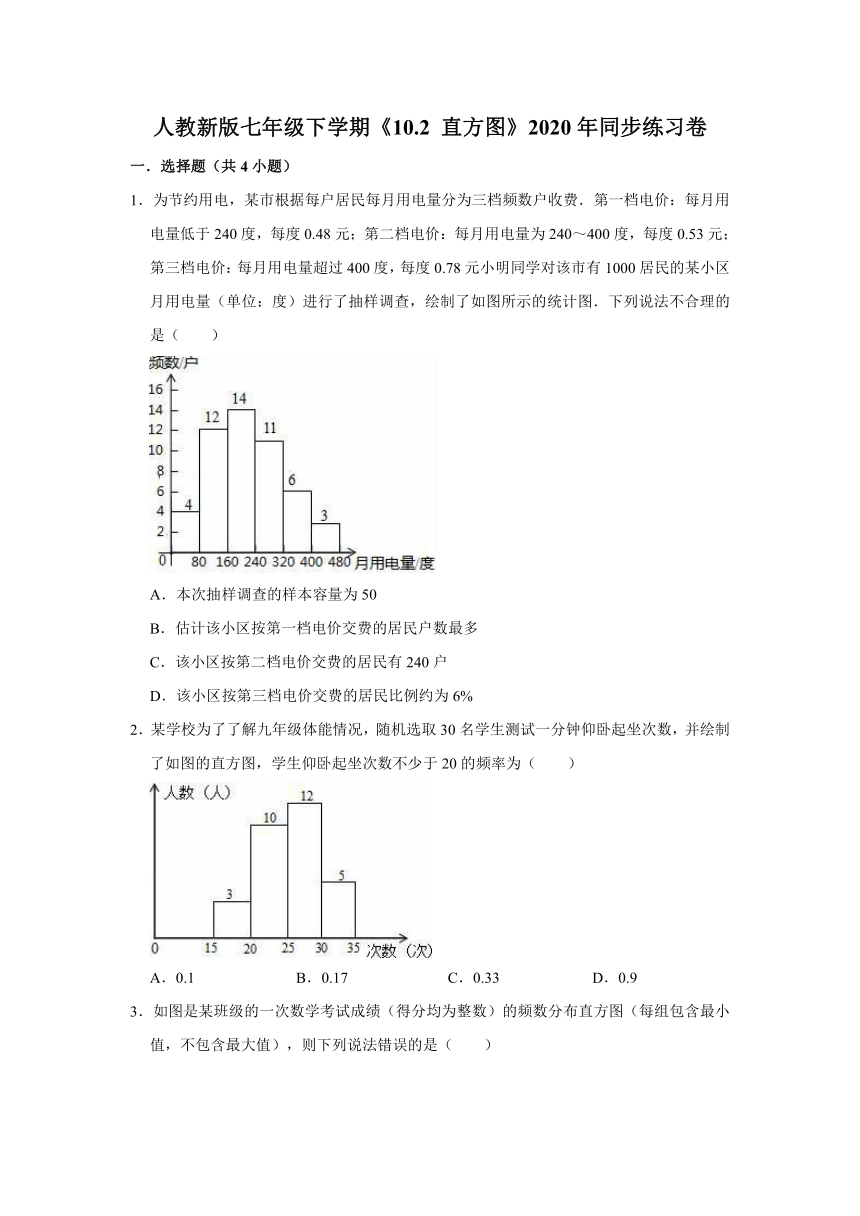
1.为节约用电,某市根据每户居民每月用电量分为三档频数户收费.第一档电价:每月用电量低于240度,每度0.48元;第二档电价:每月用电量为240~400度,每度0.53元;第三档电价:每月用电量超过400度,每度0.78元小明同学对该市有1000居民的某小区月用电量(单位:度)进行了抽样调查,绘制了如图所示的统计图.下列说法不合理的是( )
A.本次抽样调查的样本容量为50
B.估计该小区按第一档电价交费的居民户数最多
C.该小区按第二档电价交费的居民有240户
D.该小区按第三档电价交费的居民比例约为6%
2.某学校为了了解九年级体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数不少于20的频率为( )
A.0.1 B.0.17 C.0.33 D.0.9
3.如图是某班级的一次数学考试成绩(得分均为整数)的频数分布直方图(每组包含最小值,不包含最大值),则下列说法错误的是( )
A.得分在70~79分的人数最多
B.人数最少的得分段的频数为2
C.得分及格(≥60分)的有12人
D.该班的总人数为40人
4.社会主义核心价值观知识竞赛成绩结果统计如下表:成绩在91~100分的为优胜者,则优胜者的频率是( )
分段数(分) 61~70 71~80 81~90 91~100
人数(人) 1 19 22 18
A.35% B.30% C.20% D.10%
二.填空题(共5小题)
5.一个容量为80的样本最大值是136,最小值是52,用频数分布直方图描述这一数据,取组距为10,则可以分成 组.
6.在频数分布直方图中,各个小组的频数比为2:5:6:3,则对应的小长方形的高的比为 .
7.在频数分布直方图中,有5个小长方形,若正中间1个小长方形的面积等于其它4个小长方形面积和的,且共有100个数据,则正中间一组的频数为 .
8.某校开展捐书活动,七(1)班同学积极参与,现将捐书数量绘制成频数分布直方图(如图所示),如果捐书数量在3.5﹣4.5组别的人数占总人数的,那么捐书数量在4.5﹣5.5组别的人数是 .
9.某校在“数学小论文“评比活动中,共征集到论文100篇,对论文评比的分数(分数为整数)整理后,分组画出频数分布直方图(如图),已知从左到右5个小长方形的高的比为1:3:7:6:3,那么在这次评比中被评为优秀的论文(分数大于或等于80分为优秀)有 篇.
三.解答题(共7小题)
10.从共享单车,共享汽车等共享出行到共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速的普及,根据国家信息中心发布的中国分享经济发展报告2017显示,参与共享经济活动超6 亿人,比上一年增加约1亿人.
(1)为获得北京市市民参与共享经济活动信息,下列调查方式中比较合理的是 ;
A.对某学校的全体同学进行问卷调查
B.对某小区的住户进行问卷调查
C.在全市里的不同区县,选取部分市民进行问卷调查
(2)调查小组随机调查了延庆区市民骑共享单车情况,某社区年龄在12~36岁的人有1000人,从中随机抽取了100人,统计了他们骑共享单车的人数,并绘制了如下不完整的统计图表.如图所示.
骑共享单车的人数统计表
年龄段(岁) 频数 频率
12≤x<16 2 0.02
16≤x<20 3 0.03
20≤x<24 15 a
24≤x<28 25 0.25
28≤x<32 b 0.30
32≤x<36 25 0.25
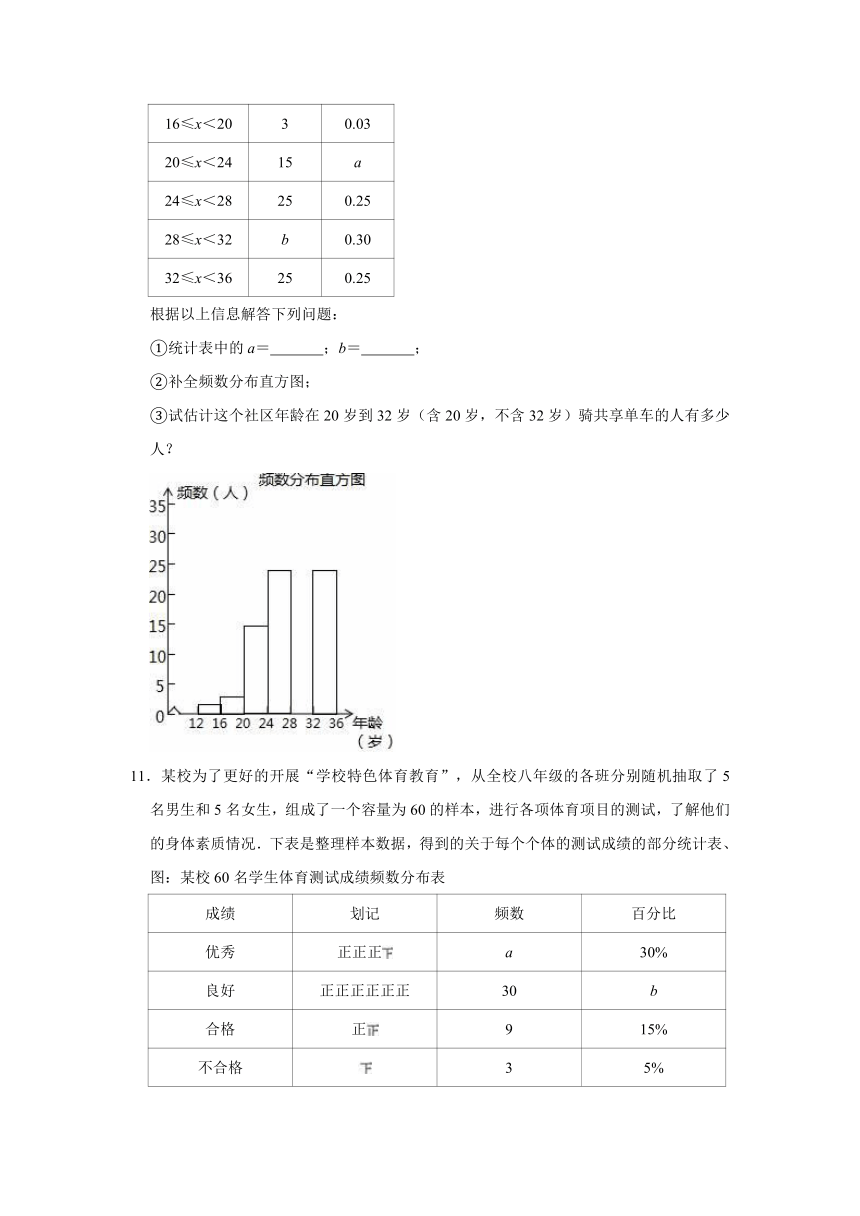
根据以上信息解答下列问题:
①统计表中的a= ;b= ;
②补全频数分布直方图;
③试估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有多少人?
11.某校为了更好的开展“学校特色体育教育”,从全校八年级的各班分别随机抽取了5名男生和5名女生,组成了一个容量为60的样本,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
成绩 划记 频数 百分比
优秀 正正正 a 30%
良好 正正正正正正 30 b
合格 正 9 15%
不合格 3 5%
合计 60 60 100%
(说明:40﹣﹣﹣55分为不合格,55﹣﹣﹣70分为合格,70﹣﹣﹣85分为良好,85﹣﹣﹣100分为优秀)请根据以上信息,解答下列问题:
(1)表中的a= ,b= ;
(2)请根据频数分布表,画出相应的频数分布直方图;
(3)如果该校八年级共有150名学生,根据以上数据,估计该校八年级学生身体素质良好及以上的人数为 .
12.某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) 频数(人数) 频率
2≤t<3 4 0.1
3≤t<4 10 0.25
4≤t<5 a 0.15
5≤t<6 8 b
6≤t<7 12 0.3
合计 40 1
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?
13.为弘扬中华传统文化,了解学生整体听写能力,某校组织全校1000名学生进行一次汉字听写大赛初赛,从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制出了频数分布表和频数分布直方图:
分组/分 频数 频率
50≤x<60 6 0.12
60≤x<70 a 0.28
70≤x<80 16 0.32
80≤x<90 10 0.20
90≤x≤100 c b
合计 50 1.00
(1)表中的a= ,b= ,c= ;
(2)把上面的频数分布直方图补充完整,并画出频数分布折线图;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加进入决赛,那么请你估计该校进入决赛的学生大约有多少人.
14.为进一步了解某校七年级(2)班同学们的身体素质,体育老师对七年级(2)班的50名学生进行了一分钟跳绳次数测试,以测试成绩为样本,绘制出部分频数分布表和部分频数分布直方图,请结合两种图表完成下列问题:
(1)表中的a=
(2)把频数分布直方图补充完整
(3)若七年级学生每分钟跳绳的次数不小于120为合格,那么,这个七年级(2)班学生跳绳的合格率为多少?
组别 次数(x) 频数
第一组 80≤x<100 6
第二组 100≤x<120 8
第三组 120≤x<140 a
第四组 140≤x<160 18
第五组 160≤x<180 6
15.某市对参加2016年中考的4000名初中毕业生进行了一次视力抽样调查,并根据统计数据,制作了如图所示的统计表和统计图.
组别 视力 频数(人)
A 4.0≤x<4.3 20
B 4.3≤x<4.6 a
C 4.6≤x<4.9 b
D 4.9≤x<5.2 70
E 5.2≤x<5.5 10
请根据图表信息回答下列问题:
(1)求抽样调查的人数;
(2)a= ,b= ,m= ;
(3)补全频数分布直方图;
(4)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是 ;根据上述信息估计该市2016年中考的初中毕业生视力正常的学生大约有多少人.
16.为了调查居民的生活水平,有关部门对某居委会的50户居民的家庭存款额进行了调查,数据(单位:万元)如下:
1.7 3.5 2.3 6.4 2.0 1.9 6.7 4.8 5.0 4.7
2.3 3.4 5.6 3.7 2.2 3.3 5.8 4.3 3.6 3.8
3.0 5.1 7.0 3.1 2.9 4.9 5.8 3.6 3.0 4.2
4.0 3.9 5.1 6.3 1.8 3.2 5.1 5.7 3.9 3.1
2.5 2.8 4.5 4.9 5.3 2.6 7.2 1.9 5.0 3.8
(1)这50个家庭存款额的最大值、最小值分别是多少?它们相差多少?
(2)填表:
存款额x(万元) 划记 户数
1.0≤x<2.0
2.0≤x<3.0
3.0≤x<4.0
4.0≤x<5.0
5.0≤x<6.0
6.0≤x<7.0
7.0≤x<8.0
(3)根据上表谈谈这50户家庭存款额的分布情况.
人教新版七年级下学期《10.2 直方图》2020年同步练习卷
参考答案与试题解析
一.选择题(共4小题)
1.为节约用电,某市根据每户居民每月用电量分为三档频数户收费.第一档电价:每月用电量低于240度,每度0.48元;第二档电价:每月用电量为240~400度,每度0.53元;第三档电价:每月用电量超过400度,每度0.78元小明同学对该市有1000居民的某小区月用电量(单位:度)进行了抽样调查,绘制了如图所示的统计图.下列说法不合理的是( )
A.本次抽样调查的样本容量为50
B.估计该小区按第一档电价交费的居民户数最多
C.该小区按第二档电价交费的居民有240户
D.该小区按第三档电价交费的居民比例约为6%
【分析】利用直方图中的信息一一判断即可.
【解答】解:本次抽样调查的样本容量=4+12+14+11+6+3=50(户),故A不符合题意.
估计该小区按第一档电价交费的居民户数占=60%,第二档占=34%,第三档占=6%,故B,D不符合题意.
该小区按第二档电价交费的居民约为1000×34%=340(户),故C符合题意,
故选:C.
【点评】本题考查频数分布直方图,样本估计总体的思想等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
2.某学校为了了解九年级体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数不少于20的频率为( )
A.0.1 B.0.17 C.0.33 D.0.9
【分析】用不少于20次的人数除以总人数可得答案.
【解答】解:由图知,学生仰卧起坐次数不少于20的人数为10+12+5=27(人),
所以学生仰卧起坐次数不少于20的频率为27÷30=0.9,
故选:D.
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
3.如图是某班级的一次数学考试成绩(得分均为整数)的频数分布直方图(每组包含最小值,不包含最大值),则下列说法错误的是( )
A.得分在70~79分的人数最多
B.人数最少的得分段的频数为2
C.得分及格(≥60分)的有12人
D.该班的总人数为40人
【分析】观察条形图即可一一判断.
【解答】解:A、得分在70~79分的人数最多,正确,本选项不符合题意.
B、人数最少的得分段的频数为2,正确,本选项不符合题意.
C、得分及格(≥60分)的有12人,错误,本选项符合题意.
D、该班的总人数为40人,正确,本选项不符合题意.
故选:C.
【点评】本题考查频数分布直方图,解题的关键是读懂图象信息,属于中考常考题型.
4.社会主义核心价值观知识竞赛成绩结果统计如下表:成绩在91~100分的为优胜者,则优胜者的频率是( )
分段数(分) 61~70 71~80 81~90 91~100
人数(人) 1 19 22 18
A.35% B.30% C.20% D.10%
【分析】首先根据表格,计算其总人数;再根据频率=频数÷总数进行计算.
【解答】解:优胜者的频率是18÷(1+19+22+18)=0.3=30%,
故选:B.
【点评】本题考查频率、频数的关系:频率=频数÷数据总和.
二.填空题(共5小题)
5.一个容量为80的样本最大值是136,最小值是52,用频数分布直方图描述这一数据,取组距为10,则可以分成 9 组.
【分析】求出最大值和最小值的差,然后除以组距,用进一法取整数值就是组数.
【解答】解:136﹣52=84,
84÷10=8.4,
所以应该分成9组,
故答案为:9.
【点评】本题考查频率分布表中组数的确定,关键是求出最大值和最小值的差,然后除以组距,用进一法取整数值就是组数.
6.在频数分布直方图中,各个小组的频数比为2:5:6:3,则对应的小长方形的高的比为 2:5:6:3 .
【分析】根据在一个调查过程中,将所有数据分成四组,各个小组的频数比为2:5:6:3,可以求得画频数分布直方图时对应的小长方形的高的比,本题得以解决.
【解答】解:∵在一个调查过程中,将所有数据分成四组,各个小组的频数比为2:5:6:3,
∴画频数分布直方图时对应的小长方形的高的比为2:5:6:3,
故答案为:2:5:6:3,
【点评】本题考查频数分布直方图,解题的关键是明确频数分布直方图的画法.
7.在频数分布直方图中,有5个小长方形,若正中间1个小长方形的面积等于其它4个小长方形面积和的,且共有100个数据,则正中间一组的频数为 20 .
【分析】直接利用5个小长方形之间面积关系得出中间一个小长方形的面积与总体面积的关系进而得出答案.
【解答】解:∵在频数分布直方图中,共有5个小长方形,若中间一个小长方形的面积等于其他4个小长方形的面积的和的,
∴设中间一个小长方形的面积为x,则其他4个小长方形的面积的和为4x,
∵共有100个数据,
∴中间有一组数据的频数是:×100=20.
故答案为20.
【点评】此题主要考查了频数分布直方图,正确得出中间一个小长方形的面积与总体面积的关系是解题关键.
8.某校开展捐书活动,七(1)班同学积极参与,现将捐书数量绘制成频数分布直方图(如图所示),如果捐书数量在3.5﹣4.5组别的人数占总人数的,那么捐书数量在4.5﹣5.5组别的人数是 16人 .
【分析】根据捐书数量在3.5﹣4.5组别的频数是12、频率是0.3,由频率=频数÷总数求得总人数,根据频数之和等于总数可得答案.
【解答】解:∵被调查的总人数为12÷=40(人),
∴捐书数量在4.5﹣5.5组别的人数是40﹣(4+12+8)=16(人),
故答案为:16人.
【点评】本题主要考查频数(率)分布表,掌握频率=频数÷总数是解题的关键.
9.某校在“数学小论文“评比活动中,共征集到论文100篇,对论文评比的分数(分数为整数)整理后,分组画出频数分布直方图(如图),已知从左到右5个小长方形的高的比为1:3:7:6:3,那么在这次评比中被评为优秀的论文(分数大于或等于80分为优秀)有 45 篇.
【分析】根据题意和频数分布直方图中的数据可以求得在这次评比中被评为优秀的论文的篇数.
【解答】解:由题意可得,
在这次评比中被评为优秀的论文(分数大于或等于80分为优秀)有:100×=45(篇),
故答案为:45.
【点评】本题考查频数分布直方图,解答本题的关键是明确题意,利用数形结合的思想解答.
三.解答题(共7小题)
10.从共享单车,共享汽车等共享出行到共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速的普及,根据国家信息中心发布的中国分享经济发展报告2017显示,参与共享经济活动超6 亿人,比上一年增加约1亿人.
(1)为获得北京市市民参与共享经济活动信息,下列调查方式中比较合理的是 C ;
A.对某学校的全体同学进行问卷调查
B.对某小区的住户进行问卷调查
C.在全市里的不同区县,选取部分市民进行问卷调查
(2)调查小组随机调查了延庆区市民骑共享单车情况,某社区年龄在12~36岁的人有1000人,从中随机抽取了100人,统计了他们骑共享单车的人数,并绘制了如下不完整的统计图表.如图所示.
骑共享单车的人数统计表
年龄段(岁) 频数 频率
12≤x<16 2 0.02
16≤x<20 3 0.03
20≤x<24 15 a
24≤x<28 25 0.25
28≤x<32 b 0.30
32≤x<36 25 0.25
根据以上信息解答下列问题:
①统计表中的a= 0.15 ;b= 30 ;
②补全频数分布直方图;
③试估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有多少人?
【分析】(1)根据抽样调查的定义可得;
(2)①根据“频率=频数÷总数”可分别求得a、b的值;
②由①中所求数据可补全图形;
③总人数乘以样本中第3、4、5组的频率之和可得答案.
【解答】解:(1)调查方式中比较合理的是C,
故答案为:C;
(2)①a=15÷100=0.15,b=100×0.3=30,
故答案为:0.15,30;
②补全图形如下:
③1000×(0.15+0.25+0.3)=700(人),
答:估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有700人.
【点评】本题考查条形图、频率分布表、样本估计总体等知识,解题的关键是记住频率=频数÷总数,频率之和为1,属于中考常考题型.
11.某校为了更好的开展“学校特色体育教育”,从全校八年级的各班分别随机抽取了5名男生和5名女生,组成了一个容量为60的样本,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
成绩 划记 频数 百分比
优秀 正正正 a 30%
良好 正正正正正正 30 b
合格 正 9 15%
不合格 3 5%
合计 60 60 100%
(说明:40﹣﹣﹣55分为不合格,55﹣﹣﹣70分为合格,70﹣﹣﹣85分为良好,85﹣﹣﹣100分为优秀)请根据以上信息,解答下列问题:
(1)表中的a= 18 ,b= 50% ;
(2)请根据频数分布表,画出相应的频数分布直方图;
(3)如果该校八年级共有150名学生,根据以上数据,估计该校八年级学生身体素质良好及以上的人数为 120 .
【分析】(1)根据样本容量和百分比求出频数,根据样本容量和频数求出百分比;
(2)根据频数画出频数分布直方图;
(3)求出八年级学生身体素质良好及以上的人数的百分比,根据总人数求出答案.
【解答】解:(1)60×30%=18,
30÷60×100%=50%,
∴a=18,b=50%;
(2)如图,
(3)150×(30%+50%)=120.
【点评】本题考查读频数分布表的能力和利用统计图获取信息的能力,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
12.某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) 频数(人数) 频率
2≤t<3 4 0.1
3≤t<4 10 0.25
4≤t<5 a 0.15
5≤t<6 8 b
6≤t<7 12 0.3
合计 40 1
(1)表中的a= 6 ,b= 0.2 ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?
【分析】(1)根据题意列式计算即可;
(2)根据b的值画出直方图即可;
(3)利用样本估计总体的思想解决问题即可;
【解答】解:(1)总人数=4÷0.1=40,
∴a=40×0.15=6,b==0.2;
故答案为6,0.2
(2)频数分布直方图如图所示:
(3)由题意得,估计全校每周在校参加体育锻炼时间至少有4小时的学生约为1200×(0.15+0.2+0.3)=780名.
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
13.为弘扬中华传统文化,了解学生整体听写能力,某校组织全校1000名学生进行一次汉字听写大赛初赛,从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制出了频数分布表和频数分布直方图:
分组/分 频数 频率
50≤x<60 6 0.12
60≤x<70 a 0.28
70≤x<80 16 0.32
80≤x<90 10 0.20
90≤x≤100 c b
合计 50 1.00
(1)表中的a= 14 ,b= 0.08 ,c= 4 ;
(2)把上面的频数分布直方图补充完整,并画出频数分布折线图;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加进入决赛,那么请你估计该校进入决赛的学生大约有多少人.
【分析】(1)根据频率分布表确定出总人数,进而求出a,b,c的值即可;
(2)把上面的频数分布直方图补充完整,并画出频数分布折线图,如图所示;
(3)根据样本中90分及90分以上的百分比,乘以1000即可得到结果.
【解答】解:(1)根据题意得:a=6÷0.12×0.28=14,b=1﹣(0.12+0.28+0.32+0.20)=0.08,c=6÷0.12×0.08=4;
故答案为:14;0.08;4;
(2)频数分布直方图、折线图如图,
(3)根据题意得:1000×(4÷50)=80(人),
则你估计该校进入决赛的学生大约有80人.
【点评】此题考查了频数(率)分布折线图,用样本估计总体,频数(率)分布表,以及频数(率)分布直方图,弄清题中的数据是解本题的关键.
14.为进一步了解某校七年级(2)班同学们的身体素质,体育老师对七年级(2)班的50名学生进行了一分钟跳绳次数测试,以测试成绩为样本,绘制出部分频数分布表和部分频数分布直方图,请结合两种图表完成下列问题:
(1)表中的a= 12
(2)把频数分布直方图补充完整
(3)若七年级学生每分钟跳绳的次数不小于120为合格,那么,这个七年级(2)班学生跳绳的合格率为多少?
组别 次数(x) 频数
第一组 80≤x<100 6
第二组 100≤x<120 8
第三组 120≤x<140 a
第四组 140≤x<160 18
第五组 160≤x<180 6
【分析】(1)根据频数分布表和题意可以求得a的值;
(2)根据频数分布表中的数据和a的值可以将频数分布直方图补充完整;
(3)根据频数分布表中的数据可以求得合格率.
【解答】解:(1)a=50﹣6﹣8﹣18﹣6=12,
故答案为:12;
(2)第三组的频数是12,第四组的频数是18,
补充完整的频数分布直方图如右图所示;
(3)=72%,
答:这个七年级(2)班学生跳绳的合格率是72%.
【点评】本题考查频数分布表、频数分布直方图,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
15.某市对参加2016年中考的4000名初中毕业生进行了一次视力抽样调查,并根据统计数据,制作了如图所示的统计表和统计图.
组别 视力 频数(人)
A 4.0≤x<4.3 20
B 4.3≤x<4.6 a
C 4.6≤x<4.9 b
D 4.9≤x<5.2 70
E 5.2≤x<5.5 10
请根据图表信息回答下列问题:
(1)求抽样调查的人数;
(2)a= 40 ,b= 60 ,m= 30 ;
(3)补全频数分布直方图;
(4)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是 40% ;根据上述信息估计该市2016年中考的初中毕业生视力正常的学生大约有多少人.
【分析】(1)先根据4.0≤x<4.3的频数除以频率求出被调查的总人数,
(2)用总人数乘以频率20%计算即可得到a,用总人数减去其他频数求出b,再用b除以总人数,即可求出m的值;
(3)根据(2)求出a,b的值,即可补全统计图;
(4)求出后两组的频率之和即可求出视力正常的人数占被统计人数的百分比,用总人数乘以所占的百分比即可得解.
【解答】解:(1)抽样调查的人数是:20÷10%=200人;
(2)a=200×20%=40(人);
b=200﹣20﹣40﹣70﹣10=60(人);
m%=×100%=30%,则m=30;
故答案为:40,60,30;
(3)根据(2)求出a,b的值,补图如下:
(4)视力正常的人数占被统计人数的百分比是:35%+5%=40%;
根据题意得:
4000×40%=1600(人),
答:该市2016年中考的初中毕业生视力正常的学生大约有1600人.
故答案为:40%.
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
16.为了调查居民的生活水平,有关部门对某居委会的50户居民的家庭存款额进行了调查,数据(单位:万元)如下:
1.7 3.5 2.3 6.4 2.0 1.9 6.7 4.8 5.0 4.7
2.3 3.4 5.6 3.7 2.2 3.3 5.8 4.3 3.6 3.8
3.0 5.1 7.0 3.1 2.9 4.9 5.8 3.6 3.0 4.2
4.0 3.9 5.1 6.3 1.8 3.2 5.1 5.7 3.9 3.1
2.5 2.8 4.5 4.9 5.3 2.6 7.2 1.9 5.0 3.8
(1)这50个家庭存款额的最大值、最小值分别是多少?它们相差多少?
(2)填表:
存款额x(万元) 划记 户数
1.0≤x<2.0 4
2.0≤x<3.0 8
3.0≤x<4.0 15
4.0≤x<5.0 8
5.0≤x<6.0 10
6.0≤x<7.0 3
7.0≤x<8.0 2
(3)根据上表谈谈这50户家庭存款额的分布情况.
【分析】(1)根据已知数据找出存款额的最大值、最小值,并求出它们的差即可;
(2)通过划记的方式即可得到各组的频数;
(3)根据频数分布表中的数据,可得这50户家庭存款额的分布情况.
【解答】解:(1)存款额的最大值为7.2万元,存款额的最小值为1.7万元,相差:7.2﹣1.7=5.5(万元);
(2)根据划记可得,1.0≤x<2.0一组的户数为4,2.0≤x<3.0一组的户数为8,3.0≤x<4.0一组的户数为15,4.0≤x<5.0一组的户数为8,5.0≤x<6.0一组的户数为10,6.0≤x<7.0一组的户数为3,7.0≤x<8.0一组的户数为2;
故答案为:4,8,15,8,10,3,2.
(3)由表可得,这50户家庭中,存款额在2.0≤x<6.0范围内的户数较多,其中在3.0≤x<4.0范围内的户数最多,而存款额在1.0≤x<2.0,6.0≤x<8.0范围内户数较少,占小部分.
【点评】本题主要考查了频数分布表,考核了学生利用统计图表获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
一.选择题(共4小题)
1.为节约用电,某市根据每户居民每月用电量分为三档频数户收费.第一档电价:每月用电量低于240度,每度0.48元;第二档电价:每月用电量为240~400度,每度0.53元;第三档电价:每月用电量超过400度,每度0.78元小明同学对该市有1000居民的某小区月用电量(单位:度)进行了抽样调查,绘制了如图所示的统计图.下列说法不合理的是( )
A.本次抽样调查的样本容量为50
B.估计该小区按第一档电价交费的居民户数最多
C.该小区按第二档电价交费的居民有240户
D.该小区按第三档电价交费的居民比例约为6%
2.某学校为了了解九年级体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数不少于20的频率为( )
A.0.1 B.0.17 C.0.33 D.0.9
3.如图是某班级的一次数学考试成绩(得分均为整数)的频数分布直方图(每组包含最小值,不包含最大值),则下列说法错误的是( )
A.得分在70~79分的人数最多
B.人数最少的得分段的频数为2
C.得分及格(≥60分)的有12人
D.该班的总人数为40人
4.社会主义核心价值观知识竞赛成绩结果统计如下表:成绩在91~100分的为优胜者,则优胜者的频率是( )
分段数(分) 61~70 71~80 81~90 91~100
人数(人) 1 19 22 18
A.35% B.30% C.20% D.10%
二.填空题(共5小题)
5.一个容量为80的样本最大值是136,最小值是52,用频数分布直方图描述这一数据,取组距为10,则可以分成 组.
6.在频数分布直方图中,各个小组的频数比为2:5:6:3,则对应的小长方形的高的比为 .
7.在频数分布直方图中,有5个小长方形,若正中间1个小长方形的面积等于其它4个小长方形面积和的,且共有100个数据,则正中间一组的频数为 .
8.某校开展捐书活动,七(1)班同学积极参与,现将捐书数量绘制成频数分布直方图(如图所示),如果捐书数量在3.5﹣4.5组别的人数占总人数的,那么捐书数量在4.5﹣5.5组别的人数是 .
9.某校在“数学小论文“评比活动中,共征集到论文100篇,对论文评比的分数(分数为整数)整理后,分组画出频数分布直方图(如图),已知从左到右5个小长方形的高的比为1:3:7:6:3,那么在这次评比中被评为优秀的论文(分数大于或等于80分为优秀)有 篇.
三.解答题(共7小题)
10.从共享单车,共享汽车等共享出行到共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速的普及,根据国家信息中心发布的中国分享经济发展报告2017显示,参与共享经济活动超6 亿人,比上一年增加约1亿人.
(1)为获得北京市市民参与共享经济活动信息,下列调查方式中比较合理的是 ;
A.对某学校的全体同学进行问卷调查
B.对某小区的住户进行问卷调查
C.在全市里的不同区县,选取部分市民进行问卷调查
(2)调查小组随机调查了延庆区市民骑共享单车情况,某社区年龄在12~36岁的人有1000人,从中随机抽取了100人,统计了他们骑共享单车的人数,并绘制了如下不完整的统计图表.如图所示.
骑共享单车的人数统计表
年龄段(岁) 频数 频率
12≤x<16 2 0.02
16≤x<20 3 0.03
20≤x<24 15 a
24≤x<28 25 0.25
28≤x<32 b 0.30
32≤x<36 25 0.25
根据以上信息解答下列问题:
①统计表中的a= ;b= ;
②补全频数分布直方图;
③试估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有多少人?
11.某校为了更好的开展“学校特色体育教育”,从全校八年级的各班分别随机抽取了5名男生和5名女生,组成了一个容量为60的样本,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
成绩 划记 频数 百分比
优秀 正正正 a 30%
良好 正正正正正正 30 b
合格 正 9 15%
不合格 3 5%
合计 60 60 100%
(说明:40﹣﹣﹣55分为不合格,55﹣﹣﹣70分为合格,70﹣﹣﹣85分为良好,85﹣﹣﹣100分为优秀)请根据以上信息,解答下列问题:
(1)表中的a= ,b= ;
(2)请根据频数分布表,画出相应的频数分布直方图;
(3)如果该校八年级共有150名学生,根据以上数据,估计该校八年级学生身体素质良好及以上的人数为 .
12.某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) 频数(人数) 频率
2≤t<3 4 0.1
3≤t<4 10 0.25
4≤t<5 a 0.15
5≤t<6 8 b
6≤t<7 12 0.3
合计 40 1
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?
13.为弘扬中华传统文化,了解学生整体听写能力,某校组织全校1000名学生进行一次汉字听写大赛初赛,从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制出了频数分布表和频数分布直方图:
分组/分 频数 频率
50≤x<60 6 0.12
60≤x<70 a 0.28
70≤x<80 16 0.32
80≤x<90 10 0.20
90≤x≤100 c b
合计 50 1.00
(1)表中的a= ,b= ,c= ;
(2)把上面的频数分布直方图补充完整,并画出频数分布折线图;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加进入决赛,那么请你估计该校进入决赛的学生大约有多少人.
14.为进一步了解某校七年级(2)班同学们的身体素质,体育老师对七年级(2)班的50名学生进行了一分钟跳绳次数测试,以测试成绩为样本,绘制出部分频数分布表和部分频数分布直方图,请结合两种图表完成下列问题:
(1)表中的a=
(2)把频数分布直方图补充完整
(3)若七年级学生每分钟跳绳的次数不小于120为合格,那么,这个七年级(2)班学生跳绳的合格率为多少?
组别 次数(x) 频数
第一组 80≤x<100 6
第二组 100≤x<120 8
第三组 120≤x<140 a
第四组 140≤x<160 18
第五组 160≤x<180 6
15.某市对参加2016年中考的4000名初中毕业生进行了一次视力抽样调查,并根据统计数据,制作了如图所示的统计表和统计图.
组别 视力 频数(人)
A 4.0≤x<4.3 20
B 4.3≤x<4.6 a
C 4.6≤x<4.9 b
D 4.9≤x<5.2 70
E 5.2≤x<5.5 10
请根据图表信息回答下列问题:
(1)求抽样调查的人数;
(2)a= ,b= ,m= ;
(3)补全频数分布直方图;
(4)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是 ;根据上述信息估计该市2016年中考的初中毕业生视力正常的学生大约有多少人.
16.为了调查居民的生活水平,有关部门对某居委会的50户居民的家庭存款额进行了调查,数据(单位:万元)如下:
1.7 3.5 2.3 6.4 2.0 1.9 6.7 4.8 5.0 4.7
2.3 3.4 5.6 3.7 2.2 3.3 5.8 4.3 3.6 3.8
3.0 5.1 7.0 3.1 2.9 4.9 5.8 3.6 3.0 4.2
4.0 3.9 5.1 6.3 1.8 3.2 5.1 5.7 3.9 3.1
2.5 2.8 4.5 4.9 5.3 2.6 7.2 1.9 5.0 3.8
(1)这50个家庭存款额的最大值、最小值分别是多少?它们相差多少?
(2)填表:
存款额x(万元) 划记 户数
1.0≤x<2.0
2.0≤x<3.0
3.0≤x<4.0
4.0≤x<5.0
5.0≤x<6.0
6.0≤x<7.0
7.0≤x<8.0
(3)根据上表谈谈这50户家庭存款额的分布情况.
人教新版七年级下学期《10.2 直方图》2020年同步练习卷
参考答案与试题解析
一.选择题(共4小题)
1.为节约用电,某市根据每户居民每月用电量分为三档频数户收费.第一档电价:每月用电量低于240度,每度0.48元;第二档电价:每月用电量为240~400度,每度0.53元;第三档电价:每月用电量超过400度,每度0.78元小明同学对该市有1000居民的某小区月用电量(单位:度)进行了抽样调查,绘制了如图所示的统计图.下列说法不合理的是( )
A.本次抽样调查的样本容量为50
B.估计该小区按第一档电价交费的居民户数最多
C.该小区按第二档电价交费的居民有240户
D.该小区按第三档电价交费的居民比例约为6%
【分析】利用直方图中的信息一一判断即可.
【解答】解:本次抽样调查的样本容量=4+12+14+11+6+3=50(户),故A不符合题意.
估计该小区按第一档电价交费的居民户数占=60%,第二档占=34%,第三档占=6%,故B,D不符合题意.
该小区按第二档电价交费的居民约为1000×34%=340(户),故C符合题意,
故选:C.
【点评】本题考查频数分布直方图,样本估计总体的思想等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
2.某学校为了了解九年级体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数不少于20的频率为( )
A.0.1 B.0.17 C.0.33 D.0.9
【分析】用不少于20次的人数除以总人数可得答案.
【解答】解:由图知,学生仰卧起坐次数不少于20的人数为10+12+5=27(人),
所以学生仰卧起坐次数不少于20的频率为27÷30=0.9,
故选:D.
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
3.如图是某班级的一次数学考试成绩(得分均为整数)的频数分布直方图(每组包含最小值,不包含最大值),则下列说法错误的是( )
A.得分在70~79分的人数最多
B.人数最少的得分段的频数为2
C.得分及格(≥60分)的有12人
D.该班的总人数为40人
【分析】观察条形图即可一一判断.
【解答】解:A、得分在70~79分的人数最多,正确,本选项不符合题意.
B、人数最少的得分段的频数为2,正确,本选项不符合题意.
C、得分及格(≥60分)的有12人,错误,本选项符合题意.
D、该班的总人数为40人,正确,本选项不符合题意.
故选:C.
【点评】本题考查频数分布直方图,解题的关键是读懂图象信息,属于中考常考题型.
4.社会主义核心价值观知识竞赛成绩结果统计如下表:成绩在91~100分的为优胜者,则优胜者的频率是( )
分段数(分) 61~70 71~80 81~90 91~100
人数(人) 1 19 22 18
A.35% B.30% C.20% D.10%
【分析】首先根据表格,计算其总人数;再根据频率=频数÷总数进行计算.
【解答】解:优胜者的频率是18÷(1+19+22+18)=0.3=30%,
故选:B.
【点评】本题考查频率、频数的关系:频率=频数÷数据总和.
二.填空题(共5小题)
5.一个容量为80的样本最大值是136,最小值是52,用频数分布直方图描述这一数据,取组距为10,则可以分成 9 组.
【分析】求出最大值和最小值的差,然后除以组距,用进一法取整数值就是组数.
【解答】解:136﹣52=84,
84÷10=8.4,
所以应该分成9组,
故答案为:9.
【点评】本题考查频率分布表中组数的确定,关键是求出最大值和最小值的差,然后除以组距,用进一法取整数值就是组数.
6.在频数分布直方图中,各个小组的频数比为2:5:6:3,则对应的小长方形的高的比为 2:5:6:3 .
【分析】根据在一个调查过程中,将所有数据分成四组,各个小组的频数比为2:5:6:3,可以求得画频数分布直方图时对应的小长方形的高的比,本题得以解决.
【解答】解:∵在一个调查过程中,将所有数据分成四组,各个小组的频数比为2:5:6:3,
∴画频数分布直方图时对应的小长方形的高的比为2:5:6:3,
故答案为:2:5:6:3,
【点评】本题考查频数分布直方图,解题的关键是明确频数分布直方图的画法.
7.在频数分布直方图中,有5个小长方形,若正中间1个小长方形的面积等于其它4个小长方形面积和的,且共有100个数据,则正中间一组的频数为 20 .
【分析】直接利用5个小长方形之间面积关系得出中间一个小长方形的面积与总体面积的关系进而得出答案.
【解答】解:∵在频数分布直方图中,共有5个小长方形,若中间一个小长方形的面积等于其他4个小长方形的面积的和的,
∴设中间一个小长方形的面积为x,则其他4个小长方形的面积的和为4x,
∵共有100个数据,
∴中间有一组数据的频数是:×100=20.
故答案为20.
【点评】此题主要考查了频数分布直方图,正确得出中间一个小长方形的面积与总体面积的关系是解题关键.
8.某校开展捐书活动,七(1)班同学积极参与,现将捐书数量绘制成频数分布直方图(如图所示),如果捐书数量在3.5﹣4.5组别的人数占总人数的,那么捐书数量在4.5﹣5.5组别的人数是 16人 .
【分析】根据捐书数量在3.5﹣4.5组别的频数是12、频率是0.3,由频率=频数÷总数求得总人数,根据频数之和等于总数可得答案.
【解答】解:∵被调查的总人数为12÷=40(人),
∴捐书数量在4.5﹣5.5组别的人数是40﹣(4+12+8)=16(人),
故答案为:16人.
【点评】本题主要考查频数(率)分布表,掌握频率=频数÷总数是解题的关键.
9.某校在“数学小论文“评比活动中,共征集到论文100篇,对论文评比的分数(分数为整数)整理后,分组画出频数分布直方图(如图),已知从左到右5个小长方形的高的比为1:3:7:6:3,那么在这次评比中被评为优秀的论文(分数大于或等于80分为优秀)有 45 篇.
【分析】根据题意和频数分布直方图中的数据可以求得在这次评比中被评为优秀的论文的篇数.
【解答】解:由题意可得,
在这次评比中被评为优秀的论文(分数大于或等于80分为优秀)有:100×=45(篇),
故答案为:45.
【点评】本题考查频数分布直方图,解答本题的关键是明确题意,利用数形结合的思想解答.
三.解答题(共7小题)
10.从共享单车,共享汽车等共享出行到共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速的普及,根据国家信息中心发布的中国分享经济发展报告2017显示,参与共享经济活动超6 亿人,比上一年增加约1亿人.
(1)为获得北京市市民参与共享经济活动信息,下列调查方式中比较合理的是 C ;
A.对某学校的全体同学进行问卷调查
B.对某小区的住户进行问卷调查
C.在全市里的不同区县,选取部分市民进行问卷调查
(2)调查小组随机调查了延庆区市民骑共享单车情况,某社区年龄在12~36岁的人有1000人,从中随机抽取了100人,统计了他们骑共享单车的人数,并绘制了如下不完整的统计图表.如图所示.
骑共享单车的人数统计表
年龄段(岁) 频数 频率
12≤x<16 2 0.02
16≤x<20 3 0.03
20≤x<24 15 a
24≤x<28 25 0.25
28≤x<32 b 0.30
32≤x<36 25 0.25
根据以上信息解答下列问题:
①统计表中的a= 0.15 ;b= 30 ;
②补全频数分布直方图;
③试估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有多少人?
【分析】(1)根据抽样调查的定义可得;
(2)①根据“频率=频数÷总数”可分别求得a、b的值;
②由①中所求数据可补全图形;
③总人数乘以样本中第3、4、5组的频率之和可得答案.
【解答】解:(1)调查方式中比较合理的是C,
故答案为:C;
(2)①a=15÷100=0.15,b=100×0.3=30,
故答案为:0.15,30;
②补全图形如下:
③1000×(0.15+0.25+0.3)=700(人),
答:估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有700人.
【点评】本题考查条形图、频率分布表、样本估计总体等知识,解题的关键是记住频率=频数÷总数,频率之和为1,属于中考常考题型.
11.某校为了更好的开展“学校特色体育教育”,从全校八年级的各班分别随机抽取了5名男生和5名女生,组成了一个容量为60的样本,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
成绩 划记 频数 百分比
优秀 正正正 a 30%
良好 正正正正正正 30 b
合格 正 9 15%
不合格 3 5%
合计 60 60 100%
(说明:40﹣﹣﹣55分为不合格,55﹣﹣﹣70分为合格,70﹣﹣﹣85分为良好,85﹣﹣﹣100分为优秀)请根据以上信息,解答下列问题:
(1)表中的a= 18 ,b= 50% ;
(2)请根据频数分布表,画出相应的频数分布直方图;
(3)如果该校八年级共有150名学生,根据以上数据,估计该校八年级学生身体素质良好及以上的人数为 120 .
【分析】(1)根据样本容量和百分比求出频数,根据样本容量和频数求出百分比;
(2)根据频数画出频数分布直方图;
(3)求出八年级学生身体素质良好及以上的人数的百分比,根据总人数求出答案.
【解答】解:(1)60×30%=18,
30÷60×100%=50%,
∴a=18,b=50%;
(2)如图,
(3)150×(30%+50%)=120.
【点评】本题考查读频数分布表的能力和利用统计图获取信息的能力,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
12.某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) 频数(人数) 频率
2≤t<3 4 0.1
3≤t<4 10 0.25
4≤t<5 a 0.15
5≤t<6 8 b
6≤t<7 12 0.3
合计 40 1
(1)表中的a= 6 ,b= 0.2 ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?
【分析】(1)根据题意列式计算即可;
(2)根据b的值画出直方图即可;
(3)利用样本估计总体的思想解决问题即可;
【解答】解:(1)总人数=4÷0.1=40,
∴a=40×0.15=6,b==0.2;
故答案为6,0.2
(2)频数分布直方图如图所示:
(3)由题意得,估计全校每周在校参加体育锻炼时间至少有4小时的学生约为1200×(0.15+0.2+0.3)=780名.
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
13.为弘扬中华传统文化,了解学生整体听写能力,某校组织全校1000名学生进行一次汉字听写大赛初赛,从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制出了频数分布表和频数分布直方图:
分组/分 频数 频率
50≤x<60 6 0.12
60≤x<70 a 0.28
70≤x<80 16 0.32
80≤x<90 10 0.20
90≤x≤100 c b
合计 50 1.00
(1)表中的a= 14 ,b= 0.08 ,c= 4 ;
(2)把上面的频数分布直方图补充完整,并画出频数分布折线图;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加进入决赛,那么请你估计该校进入决赛的学生大约有多少人.
【分析】(1)根据频率分布表确定出总人数,进而求出a,b,c的值即可;
(2)把上面的频数分布直方图补充完整,并画出频数分布折线图,如图所示;
(3)根据样本中90分及90分以上的百分比,乘以1000即可得到结果.
【解答】解:(1)根据题意得:a=6÷0.12×0.28=14,b=1﹣(0.12+0.28+0.32+0.20)=0.08,c=6÷0.12×0.08=4;
故答案为:14;0.08;4;
(2)频数分布直方图、折线图如图,
(3)根据题意得:1000×(4÷50)=80(人),
则你估计该校进入决赛的学生大约有80人.
【点评】此题考查了频数(率)分布折线图,用样本估计总体,频数(率)分布表,以及频数(率)分布直方图,弄清题中的数据是解本题的关键.
14.为进一步了解某校七年级(2)班同学们的身体素质,体育老师对七年级(2)班的50名学生进行了一分钟跳绳次数测试,以测试成绩为样本,绘制出部分频数分布表和部分频数分布直方图,请结合两种图表完成下列问题:
(1)表中的a= 12
(2)把频数分布直方图补充完整
(3)若七年级学生每分钟跳绳的次数不小于120为合格,那么,这个七年级(2)班学生跳绳的合格率为多少?
组别 次数(x) 频数
第一组 80≤x<100 6
第二组 100≤x<120 8
第三组 120≤x<140 a
第四组 140≤x<160 18
第五组 160≤x<180 6
【分析】(1)根据频数分布表和题意可以求得a的值;
(2)根据频数分布表中的数据和a的值可以将频数分布直方图补充完整;
(3)根据频数分布表中的数据可以求得合格率.
【解答】解:(1)a=50﹣6﹣8﹣18﹣6=12,
故答案为:12;
(2)第三组的频数是12,第四组的频数是18,
补充完整的频数分布直方图如右图所示;
(3)=72%,
答:这个七年级(2)班学生跳绳的合格率是72%.
【点评】本题考查频数分布表、频数分布直方图,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
15.某市对参加2016年中考的4000名初中毕业生进行了一次视力抽样调查,并根据统计数据,制作了如图所示的统计表和统计图.
组别 视力 频数(人)
A 4.0≤x<4.3 20
B 4.3≤x<4.6 a
C 4.6≤x<4.9 b
D 4.9≤x<5.2 70
E 5.2≤x<5.5 10
请根据图表信息回答下列问题:
(1)求抽样调查的人数;
(2)a= 40 ,b= 60 ,m= 30 ;
(3)补全频数分布直方图;
(4)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是 40% ;根据上述信息估计该市2016年中考的初中毕业生视力正常的学生大约有多少人.
【分析】(1)先根据4.0≤x<4.3的频数除以频率求出被调查的总人数,
(2)用总人数乘以频率20%计算即可得到a,用总人数减去其他频数求出b,再用b除以总人数,即可求出m的值;
(3)根据(2)求出a,b的值,即可补全统计图;
(4)求出后两组的频率之和即可求出视力正常的人数占被统计人数的百分比,用总人数乘以所占的百分比即可得解.
【解答】解:(1)抽样调查的人数是:20÷10%=200人;
(2)a=200×20%=40(人);
b=200﹣20﹣40﹣70﹣10=60(人);
m%=×100%=30%,则m=30;
故答案为:40,60,30;
(3)根据(2)求出a,b的值,补图如下:
(4)视力正常的人数占被统计人数的百分比是:35%+5%=40%;
根据题意得:
4000×40%=1600(人),
答:该市2016年中考的初中毕业生视力正常的学生大约有1600人.
故答案为:40%.
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
16.为了调查居民的生活水平,有关部门对某居委会的50户居民的家庭存款额进行了调查,数据(单位:万元)如下:
1.7 3.5 2.3 6.4 2.0 1.9 6.7 4.8 5.0 4.7
2.3 3.4 5.6 3.7 2.2 3.3 5.8 4.3 3.6 3.8
3.0 5.1 7.0 3.1 2.9 4.9 5.8 3.6 3.0 4.2
4.0 3.9 5.1 6.3 1.8 3.2 5.1 5.7 3.9 3.1
2.5 2.8 4.5 4.9 5.3 2.6 7.2 1.9 5.0 3.8
(1)这50个家庭存款额的最大值、最小值分别是多少?它们相差多少?
(2)填表:
存款额x(万元) 划记 户数
1.0≤x<2.0 4
2.0≤x<3.0 8
3.0≤x<4.0 15
4.0≤x<5.0 8
5.0≤x<6.0 10
6.0≤x<7.0 3
7.0≤x<8.0 2
(3)根据上表谈谈这50户家庭存款额的分布情况.
【分析】(1)根据已知数据找出存款额的最大值、最小值,并求出它们的差即可;
(2)通过划记的方式即可得到各组的频数;
(3)根据频数分布表中的数据,可得这50户家庭存款额的分布情况.
【解答】解:(1)存款额的最大值为7.2万元,存款额的最小值为1.7万元,相差:7.2﹣1.7=5.5(万元);
(2)根据划记可得,1.0≤x<2.0一组的户数为4,2.0≤x<3.0一组的户数为8,3.0≤x<4.0一组的户数为15,4.0≤x<5.0一组的户数为8,5.0≤x<6.0一组的户数为10,6.0≤x<7.0一组的户数为3,7.0≤x<8.0一组的户数为2;
故答案为:4,8,15,8,10,3,2.
(3)由表可得,这50户家庭中,存款额在2.0≤x<6.0范围内的户数较多,其中在3.0≤x<4.0范围内的户数最多,而存款额在1.0≤x<2.0,6.0≤x<8.0范围内户数较少,占小部分.
【点评】本题主要考查了频数分布表,考核了学生利用统计图表获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
