1.2.2函数的表示法(共19张PPT)
文档属性
| 名称 | 1.2.2函数的表示法(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-18 21:38:10 | ||
图片预览





文档简介
(共19张PPT)
函数的表示方法
教学目 标
使学生掌握函数的三种常用表示法:解析法、图象法、列表法,会用这三种方法表示函数;
教学重点: 掌握表示函数的三种常用方法,并了解它们的优劣。
教学难点: 函数解析式的求法。
实例引入:
商店销售某种瓶装饮料,售价每瓶2.5元。设购买饮料瓶数为x(瓶),
应付款为y元,则计算应付款的算式
可以清晰的反映出函数y与自变量x之间的关系。
y=2.5x
像这样,利用等式表示函数的方法叫做
这个等式叫做
函数解析式
一次函数
y=kx+b
反比例函数
二次函数
都是利用解析法表示的函数
解析法
解析法的优点:
(1)函数关系清楚;
(2)容易从自变量的值求出其对应的函数值;
(3)便于研究函数的性质。
注意:解析法表示函数是中学研究函数的主要表示方法;用解析法表示函数时,必须注明函数的定义域.
例:文具店内出售某种铅笔,每支售价为0.12元,应付款是购买铅笔数的函数,当购买6支以内(含6支)的铅笔时,请用解析法表示这个函数。
解:设购买的铅笔数为x(支),应付款为y(元),则函数的定义域为{1,2,3,4,5,6}
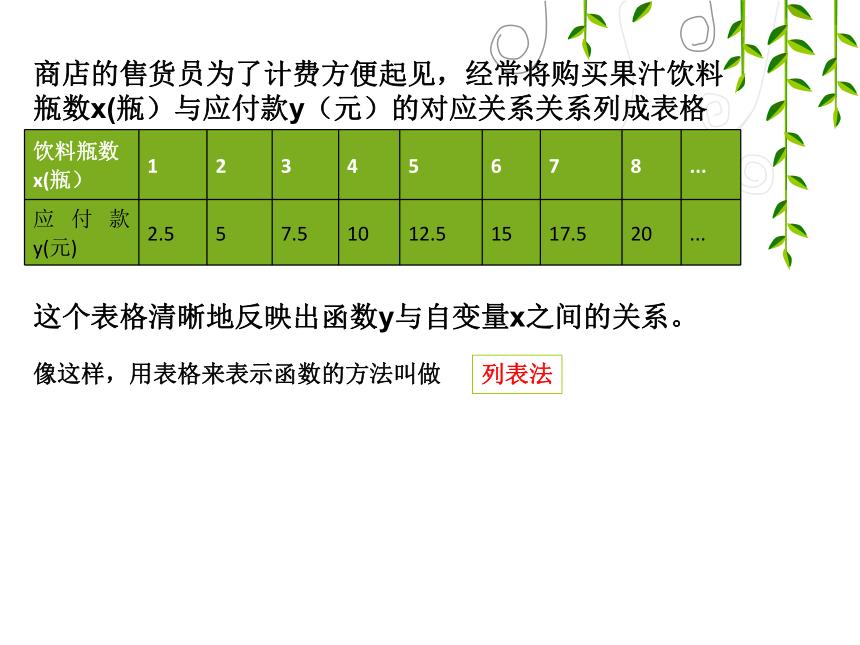
商店的售货员为了计费方便起见,经常将购买果汁饮料瓶数x(瓶)与应付款y(元)的对应关系关系列成表格
这个表格清晰地反映出函数y与自变量x之间的关系。
像这样,用表格来表示函数的方法叫做
列表法
饮料瓶数 x(瓶) 1 2 3 4 5 6 7 8 ...
应付款y(元) 2.5 5 7.5 10 12.5 15 17.5 20 ...
例如: 国内生产总值 : 单位:亿元
列表法的优点:
不必通过计算就知道当自变量取某些值时函数的对应值。
再如,某天一昼夜温度变化情况如下表
银行里的利息表,列车时刻表等等都是用列表法来表示函数关系的.公共汽车上的票价表
年份 1990 1991 1992 1993
生产总值 18598.4 21662.5 26651.9 34560.5
时刻 0:00 4:00 8:00 12:00 16:00 20:00 24:00
温度/(OC) -2 -5 4 9 8.5 3.5 -1
例:文具店内出售某种铅笔,每支售价为0.12元,应付款是购买铅笔数的函数,当购买6支以内(含6支)的铅笔时,请用列表法表示这个函数。
依照售价,分别计算出购买1~6支铅笔所需应付款,列成表格,得到函数的列表表示
x/支 1 2 3 4 5 6
y/元 0.12 0.24 0.36 0.48 0.6 0.72
知识探究
近几十年来,大气层中的臭氧迅速减少,因而出现了臭氧层空洞问题. 下图中的曲线显示了南极上空臭氧层空洞的面积从1979~2001年的变化情况.
我们知道,对于一个函数,如果把自变量x与对应的函数值y,分别作为直角坐标系中点的横坐标与纵坐标,那么由这些点组成的图形就是这个函数的图像。
像这样,用函数图像表示两个变量之间的对应关系方法叫做
例如: 我国人口出生率变化曲线:
图像法的优点:
能直观形象的表示出函数的变化情况。
图像法
如:心电图,气象台应用自动记录器描绘温度随时间变
化的曲线,股市走向图等都是用图象法表示函数关系的.
例:文具店内出售某种铅笔,每支售价为0.12元,应付款是购买铅笔数的函数,当购买6支以内(含6支)的铅笔时,请用图像法表示这个函数。
它的图像如图所示,由六个孤立的点
A (1,0.12),
B (2,0.24),
C (3,0.36),
D (4,0.48),
E (5,0.6),
F (6,0.72) 组成.
函数的图像从“形”的方面揭示了函数的变化规律,是数学的图形语言,图像法是解决函数问题的常用方法,利用函数的图像既有利于掌握各类函数的性质,又能运用“数形结合”的方法去解决某些问题。
函数的三种表示法之间具有内在联系,它们之间可以相互转化。
三种表示方法的特点
解析法的特点:简明、全面地概括了变
量间的关系;可以通过用解析式求出任意
一个自变量所对应的函数值。
列表法的特点:不通过计算就可以直接
看出与自变量的值相对应的函数值。
图象法的特点:直观形象地表示出函数
的变化情况 ,有利于通过图形研究函数的某些性质。
讨论
例:下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表.
对这三位同学在高一学年度的数学学习情况做一个分析.
第一次 第二次 第三次 第四次 第五次 第六次
王伟 98 87 91 92 88 95
张城 90 76 88 75 86 80
赵磊 68 65 73 72 75 82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
解:从表中可以知道每位同学在每次测试中的成绩,但是不容易看出每位同学的成绩的变化情况.可以将“成绩”与“测试序号”之间的关系用函数图像表示出来,如图1,那么就能比较直观地看到成绩变化的情况.
为了更容易的看出学生的学习情况,将离散的点用虚线连接。
在图2中看到,王伟同学的数学成绩始终高于班级平均水平,学习情况比较稳定而且比较优秀.张诚同学的数学成绩不稳定,总是在班级平均水平上下波动,而且幅度较大.赵磊同学的数学成绩低于平均水平,但是他的成绩呈曲线上升的趋势,从而表明他的数学成绩在稳步提高.
理解函数的三种表示方法,在具体的实际问题中能够选用恰当的表示法来表示函数;
谢谢 再见!
函数的表示方法
教学目 标
使学生掌握函数的三种常用表示法:解析法、图象法、列表法,会用这三种方法表示函数;
教学重点: 掌握表示函数的三种常用方法,并了解它们的优劣。
教学难点: 函数解析式的求法。
实例引入:
商店销售某种瓶装饮料,售价每瓶2.5元。设购买饮料瓶数为x(瓶),
应付款为y元,则计算应付款的算式
可以清晰的反映出函数y与自变量x之间的关系。
y=2.5x
像这样,利用等式表示函数的方法叫做
这个等式叫做
函数解析式
一次函数
y=kx+b
反比例函数
二次函数
都是利用解析法表示的函数
解析法
解析法的优点:
(1)函数关系清楚;
(2)容易从自变量的值求出其对应的函数值;
(3)便于研究函数的性质。
注意:解析法表示函数是中学研究函数的主要表示方法;用解析法表示函数时,必须注明函数的定义域.
例:文具店内出售某种铅笔,每支售价为0.12元,应付款是购买铅笔数的函数,当购买6支以内(含6支)的铅笔时,请用解析法表示这个函数。
解:设购买的铅笔数为x(支),应付款为y(元),则函数的定义域为{1,2,3,4,5,6}
商店的售货员为了计费方便起见,经常将购买果汁饮料瓶数x(瓶)与应付款y(元)的对应关系关系列成表格
这个表格清晰地反映出函数y与自变量x之间的关系。
像这样,用表格来表示函数的方法叫做
列表法
饮料瓶数 x(瓶) 1 2 3 4 5 6 7 8 ...
应付款y(元) 2.5 5 7.5 10 12.5 15 17.5 20 ...
例如: 国内生产总值 : 单位:亿元
列表法的优点:
不必通过计算就知道当自变量取某些值时函数的对应值。
再如,某天一昼夜温度变化情况如下表
银行里的利息表,列车时刻表等等都是用列表法来表示函数关系的.公共汽车上的票价表
年份 1990 1991 1992 1993
生产总值 18598.4 21662.5 26651.9 34560.5
时刻 0:00 4:00 8:00 12:00 16:00 20:00 24:00
温度/(OC) -2 -5 4 9 8.5 3.5 -1
例:文具店内出售某种铅笔,每支售价为0.12元,应付款是购买铅笔数的函数,当购买6支以内(含6支)的铅笔时,请用列表法表示这个函数。
依照售价,分别计算出购买1~6支铅笔所需应付款,列成表格,得到函数的列表表示
x/支 1 2 3 4 5 6
y/元 0.12 0.24 0.36 0.48 0.6 0.72
知识探究
近几十年来,大气层中的臭氧迅速减少,因而出现了臭氧层空洞问题. 下图中的曲线显示了南极上空臭氧层空洞的面积从1979~2001年的变化情况.
我们知道,对于一个函数,如果把自变量x与对应的函数值y,分别作为直角坐标系中点的横坐标与纵坐标,那么由这些点组成的图形就是这个函数的图像。
像这样,用函数图像表示两个变量之间的对应关系方法叫做
例如: 我国人口出生率变化曲线:
图像法的优点:
能直观形象的表示出函数的变化情况。
图像法
如:心电图,气象台应用自动记录器描绘温度随时间变
化的曲线,股市走向图等都是用图象法表示函数关系的.
例:文具店内出售某种铅笔,每支售价为0.12元,应付款是购买铅笔数的函数,当购买6支以内(含6支)的铅笔时,请用图像法表示这个函数。
它的图像如图所示,由六个孤立的点
A (1,0.12),
B (2,0.24),
C (3,0.36),
D (4,0.48),
E (5,0.6),
F (6,0.72) 组成.
函数的图像从“形”的方面揭示了函数的变化规律,是数学的图形语言,图像法是解决函数问题的常用方法,利用函数的图像既有利于掌握各类函数的性质,又能运用“数形结合”的方法去解决某些问题。
函数的三种表示法之间具有内在联系,它们之间可以相互转化。
三种表示方法的特点
解析法的特点:简明、全面地概括了变
量间的关系;可以通过用解析式求出任意
一个自变量所对应的函数值。
列表法的特点:不通过计算就可以直接
看出与自变量的值相对应的函数值。
图象法的特点:直观形象地表示出函数
的变化情况 ,有利于通过图形研究函数的某些性质。
讨论
例:下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表.
对这三位同学在高一学年度的数学学习情况做一个分析.
第一次 第二次 第三次 第四次 第五次 第六次
王伟 98 87 91 92 88 95
张城 90 76 88 75 86 80
赵磊 68 65 73 72 75 82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
解:从表中可以知道每位同学在每次测试中的成绩,但是不容易看出每位同学的成绩的变化情况.可以将“成绩”与“测试序号”之间的关系用函数图像表示出来,如图1,那么就能比较直观地看到成绩变化的情况.
为了更容易的看出学生的学习情况,将离散的点用虚线连接。
在图2中看到,王伟同学的数学成绩始终高于班级平均水平,学习情况比较稳定而且比较优秀.张诚同学的数学成绩不稳定,总是在班级平均水平上下波动,而且幅度较大.赵磊同学的数学成绩低于平均水平,但是他的成绩呈曲线上升的趋势,从而表明他的数学成绩在稳步提高.
理解函数的三种表示方法,在具体的实际问题中能够选用恰当的表示法来表示函数;
谢谢 再见!
