3.1倒数 课件(32张ppt)
图片预览








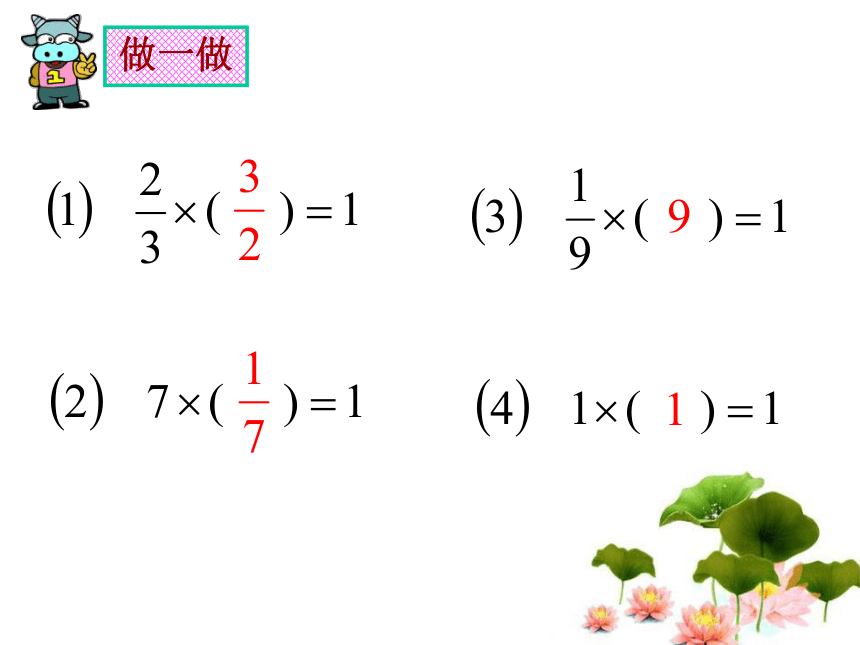

文档简介
课件32张PPT。倒 数 的 认 识呆杏吴吞学习目标
通过自学、观察、思考和讨论,认识互为倒数的两个数的关系,掌握倒数的意义,会对倒数正确表达。
掌握求一个数的倒数的方法,并能正确熟练地求出一个数的倒数.
学习方式
自学与小组合作交流相结合
评价方式
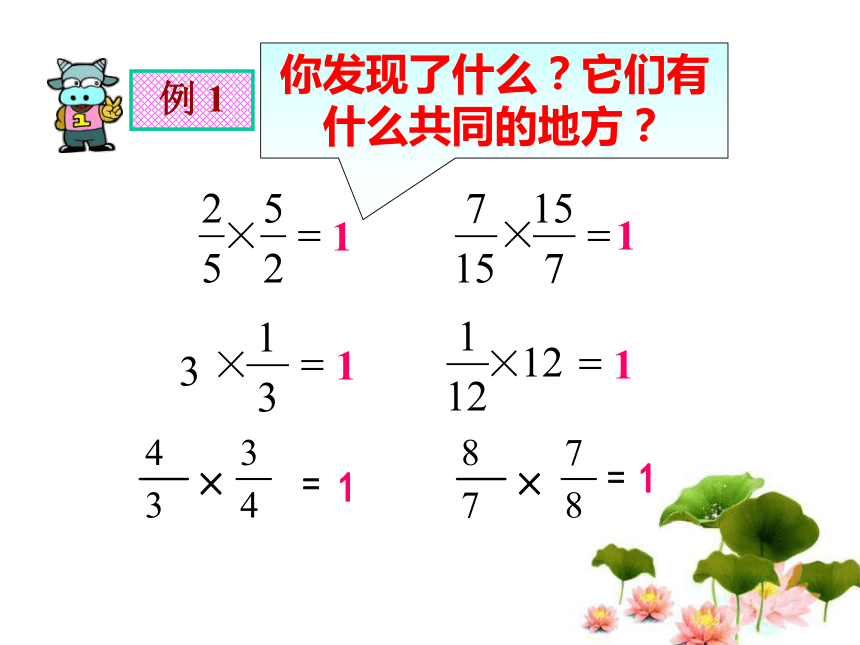
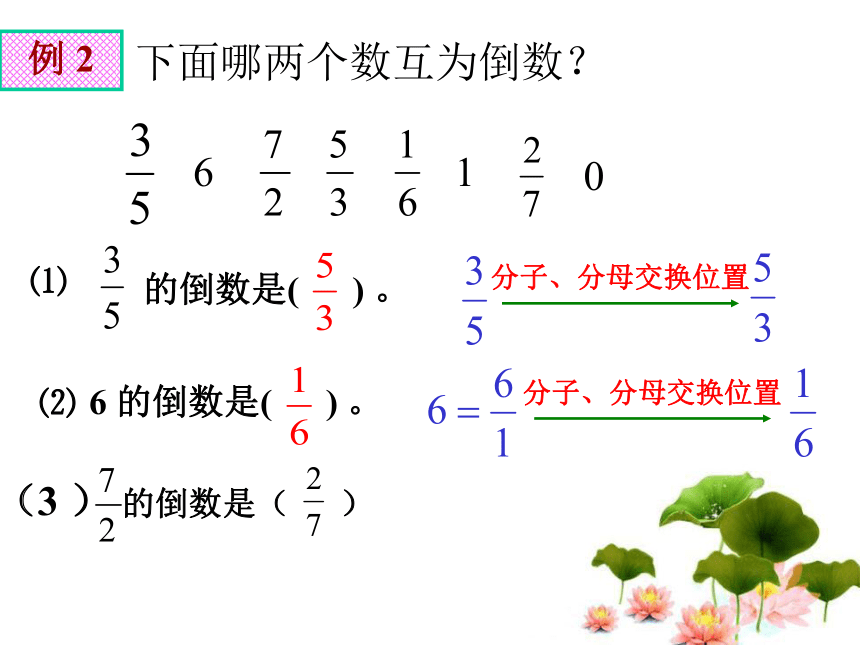
小组汇报,习题练习法。把下列整数改写成分母是1的假分数6=10=1=25=9=200=36=7=202=口算下列各题。例 1=313=12121××××1111你发现了什么?它们有什么共同的地方?×=×=11乘积是1 两个数的叫做互为倒数。你还能很快地说出几个这样的例子吗?思考讨论: 什么叫“互为”?如:因为2/5 X 5/2 = 1或者说2/5是5/2的倒数, 也可以说5/2的倒数是2/5,不能说2/5是倒数, 5/2是倒数。所以,我们就说2/5与5/2互为倒数,例 2 下面哪两个数互为倒数? (3 ) 的倒数是( )610 思考讨论:
1和0有没有倒数?
倒数是多少?求一个数 的倒数,只要把这个数的分子、分母调换位置。 (0除外)求倒数的方法:做一做说出下列各数的倒数。练一练1 练一练 2判断题。练一练 3? ⑵? ? ⑷ 一个数的倒数一定比这个数小。 ( ) ( )? 练一练 4将互为倒数的两个数用线连起来。313678133768125261001100995999592526说出下列各数的倒数。思考巩固题一.填空:
1.乘积是( )的( )个
数( )倒数。
2.a 和b互为倒数,那a的倒数是( ),b的倒数是()1两互为ba3.求一个数(0除外)的倒数的方法是(
)。
0.625× =1,( )
和( )互为倒数。只要把这个数的分子、分母调换位置0.6255.一个真分数的倒数一定是( )数,它
( )1,一个除1以外的假分数的倒数一定是一个( )数,它 ( )1;。假分大于真分小于只有当假分数为( )时,
它与它的倒数 相等;
而( )是没有倒数106. 18的 的倒数是( )
7. 乘9的倒数,积是
( )。3.整数 a 的倒数是 . ( )4.得数是1的两个数互为倒数。( )
5.任何一个数的倒数都小于它本身。( )6.真分数的倒数大于1,假分数的倒数小于1。( )
+ =1,所以 和
互为倒数。( )8.任何自然数的倒数都比它本身小。( )
9.真分数的倒数都是假分数,假分数的倒数都真分数。( )10、求一个数(0除外)的倒数只要
把分子、分母调换位置。( )
∨11、乘积是1的两个数互为倒数。( )
12、0.4和2.5互为倒数。( )
13、 是倒数。( )
14、因为1的倒数是1,所以0的倒数是0。
( )
∨∨
15、 × × =1,所以 、
互为倒数。( )
16、任何假分数的倒数都是
真分数。( )
17、真分数的倒数都大于1.( )∨同桌之间交流本节课学习收获是什么?乘积是1的两个数叫
做互为倒数。求一个数 的倒数,只要把这个数的分子、分母调换位置。 (0除外)求倒数的方法:1的倒数是1
0没有倒数自然数(0,1除外)的倒数都小于它本身。
通过自学、观察、思考和讨论,认识互为倒数的两个数的关系,掌握倒数的意义,会对倒数正确表达。
掌握求一个数的倒数的方法,并能正确熟练地求出一个数的倒数.
学习方式
自学与小组合作交流相结合
评价方式
小组汇报,习题练习法。把下列整数改写成分母是1的假分数6=10=1=25=9=200=36=7=202=口算下列各题。例 1=313=12121××××1111你发现了什么?它们有什么共同的地方?×=×=11乘积是1 两个数的叫做互为倒数。你还能很快地说出几个这样的例子吗?思考讨论: 什么叫“互为”?如:因为2/5 X 5/2 = 1或者说2/5是5/2的倒数, 也可以说5/2的倒数是2/5,不能说2/5是倒数, 5/2是倒数。所以,我们就说2/5与5/2互为倒数,例 2 下面哪两个数互为倒数? (3 ) 的倒数是( )610 思考讨论:
1和0有没有倒数?
倒数是多少?求一个数 的倒数,只要把这个数的分子、分母调换位置。 (0除外)求倒数的方法:做一做说出下列各数的倒数。练一练1 练一练 2判断题。练一练 3? ⑵? ? ⑷ 一个数的倒数一定比这个数小。 ( ) ( )? 练一练 4将互为倒数的两个数用线连起来。313678133768125261001100995999592526说出下列各数的倒数。思考巩固题一.填空:
1.乘积是( )的( )个
数( )倒数。
2.a 和b互为倒数,那a的倒数是( ),b的倒数是()1两互为ba3.求一个数(0除外)的倒数的方法是(
)。
0.625× =1,( )
和( )互为倒数。只要把这个数的分子、分母调换位置0.6255.一个真分数的倒数一定是( )数,它
( )1,一个除1以外的假分数的倒数一定是一个( )数,它 ( )1;。假分大于真分小于只有当假分数为( )时,
它与它的倒数 相等;
而( )是没有倒数106. 18的 的倒数是( )
7. 乘9的倒数,积是
( )。3.整数 a 的倒数是 . ( )4.得数是1的两个数互为倒数。( )
5.任何一个数的倒数都小于它本身。( )6.真分数的倒数大于1,假分数的倒数小于1。( )
+ =1,所以 和
互为倒数。( )8.任何自然数的倒数都比它本身小。( )
9.真分数的倒数都是假分数,假分数的倒数都真分数。( )10、求一个数(0除外)的倒数只要
把分子、分母调换位置。( )
∨11、乘积是1的两个数互为倒数。( )
12、0.4和2.5互为倒数。( )
13、 是倒数。( )
14、因为1的倒数是1,所以0的倒数是0。
( )
∨∨
15、 × × =1,所以 、
互为倒数。( )
16、任何假分数的倒数都是
真分数。( )
17、真分数的倒数都大于1.( )∨同桌之间交流本节课学习收获是什么?乘积是1的两个数叫
做互为倒数。求一个数 的倒数,只要把这个数的分子、分母调换位置。 (0除外)求倒数的方法:1的倒数是1
0没有倒数自然数(0,1除外)的倒数都小于它本身。
